基于LoRa的地下停车场车辆定位系统设计

，， ，，

(1.广西民族大学 广西混杂计算与集成电路设计分析重点实验室，南宁 530000；(2.兰州大学 信息科学与工程学院，兰州730000；3.北京计算机技术及应用研究所，北京 100000)

0 引言

地面停车场一般都有比较成熟的定位导航系统，并且大都是结合卫星导航(global positioning system，GPS)实现的[1]。在开阔的环境中，无线信号比较容易到达，GPS的定位精度可以达到米级，因此，GPS在地面停车场导航系统中得到了广泛的应用[2]。近年来，无线通信技术得到了飞速发展，GPS和蜂窝网络结合的定位技术也得到了广泛应用，成为了GPS定位系统的补充。但是，在地下和室内环境中，由于受建筑物本身和其内部结构的影响，使得GPS信号很难到达，无法得到所需要的定位数据，定位精度受到严重影响，甚至无法定位。

目前，无线室内定位技术有了迅猛发展，现有的地下和室内定位系统主要是采用超声波、红外、蓝牙、WIFI、ZigBee[3]等技术。但是，在工厂、医院、地下停车场等环境复杂的场合，现有的物联网技术存在一定的局限性，如ZigBee通信的信号穿透能力比较差，WIFI传输的距离比较短。因此，开发出一套简单化、精准化的定位系统是未来的发展趋势。

本文提出了一种低功耗窄带物联网解决方案。LoRa是LPWAN通信技术的一种，是一种基于扩频技术的超远距离的无线传输解决方案。这一方案在传输距离与功耗的折衷方面有了一定的突破，为用户提供一种远距离 、低功耗、大容量的系统[4]。LoRa主要在全球免费频段运行，包括433、868、915MHz等[5]。LoRa的技术特性可以满足本系统对远距离 、低功耗、低成本的要求。在地下停车场中合理地布局基于LoRa调制技术的锚节点，车辆进入地下停车场时获得一张同样基于LoRa调制技术的移动标签节点，来实现车辆位置的实时监测。

1 LoRa技术简介

LoRa调制技术是在线性调频扩频技术的基础上改进而来的，因为脉冲具有线性调频特质，收发装置间的频偏等于时间偏移，所以很容易在解码器中消除，所以LoRa调制可以避免多普勒效应的影响。收发器之间的频偏可以达到带宽的20%，并且不影响解码效果，发射器的晶振并不需要做到高度精准，因此LoRa调制可降低发射器成本。LoRa接收器能够自动跟踪它收到的频率，能够达到-130dBm的灵敏度。

LoRa采用典型的星型拓扑结构，和网状的网络架构比较，它具有低延时、结构简单等优点[6]。并且，还具有低成本，低功耗，低复杂度等优势，能够很好地应用到各种无线通信环境中。

2 基于TOA的测距实现

目前定位采用的基本方法主要是基于信号场强 (SOA)、基于信号到达角 (AOA)、接收信号强度(RSSI)、到达时间(TOA)或者到达时间差 (TDOA)[7]，相比较其他方法TOA定位精度比较高，且原理简单。本系统采用TOA实现测距定位，即通过测量无线电波从发射机到接收机间的传播时间来确定移动台位置的技术[8]。基于TOA对距离进行测量的方法，在环境理想情况下，能够达到比较好的测量精度。但是，在实际环境中，遮挡物的存在影响了无线电波的正常传播，影响了测距的精度，其中物理实体阻挡和散射造成的 NLOS 传播是影响定位精度的关键因素。

TOA测距原理如式(1)所示：

d=ctTOA

(1)

式中，d为锚节点与移动标签之间的距离，c为光速，tTOA为测得的锚节点与标签节点的TOA时间值。

2.1 地下停车场NLOS时延分析

(2)

式中,tTOA为信号在视距传播环境下的传播时间，tNLOS为非视距传播环境下的时延。

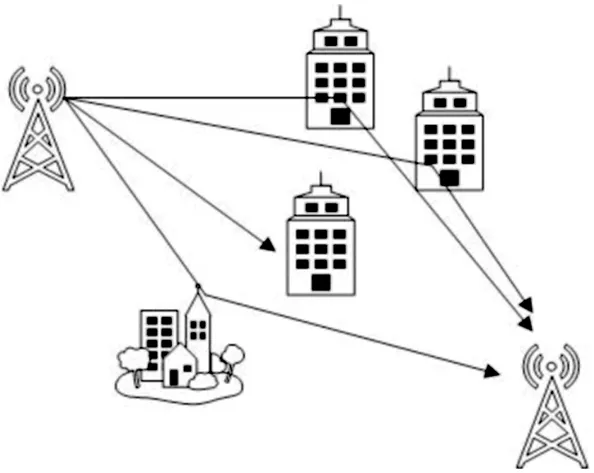
图1 NLOS传播路径图

根据文献[9]NLOS时延模型,NLOS时延扩展式可以表示为:

tNLOS=Tτdεξδξ

(3)

式中，Tτ为移动标签节点与锚节点距离为1 km时的中值，为已知的固定参数；ε为0.5 ～1.0之间的指数；ξ为服从对数分布的随机变量(即10 lgξ均值为0、标准差δξ为 4～6 dB的高斯随机变量);d为信号发射机与接收机之间的距离。

对于4种常用的通信环境中，上述参数的典型取值[10]如表1所示。

表1 典型环境参数

通过分析地下停车场特定的通信环境，依据上述时延参考模型，根据现场情况选取参数分析电磁传播的NLOS时延。

参考NLOS时延模型，NLOS时延服从指数分布， NLOS传播引起的附加时延均值和方差[10]分别为:

(4)

D(tNLOS) =(Tτdε)2e2mz + σz 2(2eσz 2)

(5)

所以，可以认为地下停车场中固定设施及结构所造成的NLOS时延，和移动标签节点和固定锚节点之间真实距离d有关，这类由于地下停车场的固定的、规律性的建筑结构造成的时延认为是NLOS的规律性时延；但是，地下停车场的环境也不是一成不变的，当地下停车场有车行驶进来时，恰巧出现在信号的传输路径上，此时，信号的传播环境出现变化，则相应NLOS 时延也会变化。车辆会对电磁波传播造成插入损耗，且属于灾难性的无法进行定量分析，所以突发性的障碍物出现在移动标签节点和锚节点之间时，会造成NLOS时延的显著增加，因为，车辆等突发性障碍物的出现具有随机性，所以，此类NLOS延时也具有显著性和突发性。

2.2 基于排序的均值滤波算法

如上述分析，在地下停车场的环境中，经常有一些随机因素出现，对定位信号的电磁波造成严重遮挡，比如当在无线电波信号传输过程中突然有车辆出现在信号的LOS传输路径上时，根据光的传播机理进行分析，电磁波必须绕过该车辆，通过新的NLOS路径到达接收端，这也就意味着该路径在停车场墙壁上发生首次反射，即要以相对较大的入射角形成发生过程。因此，发射端和接收端的传输路径将较原先的传输路径有着较大的距离增量，因为遮挡物的出现是随机的，所以，在测距的数值是以一个突发的脉冲的形式反映出来的。这类 NLOS 时延误差不具有规律性。

均值滤波算法是典型的线性滤波算法，可以对数据进行平滑处理，消除数据中的噪点。在地下停车场环境中，由于随机因素出现造成TOA测距的NLOS时延，在测距的数值上的分布是以脉冲的形式出现的。因此，可以认为采用均值滤波的方法可以对地下停车场的突发NLOS时延进行抑制。

经典均值滤波算法原理[11]为:

(6)

式中，y(n)为均值滤波后的结果，y(i)为实际测量值，M=2j+1为滤波窗口大小。

通过前面的分析可知，当车辆等随机因素出现在信号的LOS路径上时，引起的测距偏差是随机性的，造成该时刻的TOA测量值在测量值曲线上是以尖峰的形式呈现的，用均值滤波算法可以对尖峰进行很好地抑制。

均值滤波算法实质是在滤波窗口的范围内,把脉冲噪声在窗口内的各个数值上进行均摊，使数据的曲线相对平滑。在地下停车场环境中，随机因素的出现，造成TOA测量值产生突变，通过均值滤波算法，可以使测量误差减小，变得平滑，但还是无法从根本上将误差消除，并且，在随机误差出现的测量点和其附近的点都会存在误差，因此存在很大的局限性。

为克服典型均值滤波算法固有的局限性，本系统将排序算法与典型均值滤波算法相结合。标签节点在移动过程中，多次进行TOA测距操作，在测距达到设定的次数后，对多组数据进行排序，本系统使用冒泡排序的方法，按照从小到大排序，然后再对排序后的测距数据进行均值滤波，并且，均值滤波的窗口小于已测量的数据的组数，一般取排序后数据的中间若干组数据进行均值滤波。通过此方法可以很好地将TOA测量值中突发NLOS时延滤除，降低突发NLOS时延对测量值的影响，从而提高测距精度。

使用上述方法在地下停车场场景中进行测试验证，选取排序的数据组数为30，均值滤波窗口为20，测试结果如图2所示。

图2 改进的均值滤波算法测试结果图

由图2可看出，通过与典型的均值滤波算法相比分析，本文提出的算法，对测量的数据进行排序后再进行均值滤波，能够有效地滤除突发的NLOS时延造成的测量误差。

2.3 基于参数拟合的TOA时延抑制

几何光学认为高频电磁波具有似光性，因此可以采用几何光学对高频电磁波的传播进行分析。几何光学的费马原理表明: 光从空间的一点到另一点的实际路径是沿着光程为极值的路径传播的。因此，在对地下停车场NOLS时延进行分析时，可以认为: 无线信号在地下车库通信环境中从一点传播到另一点时，沿着时间最短的路径进行传播。

在NLOS传播环境下，无线电波每经历一次反射，会使LOS路径产生一个增量，把每次的反射路径作为一个路径分段进行分析，假设在NLOS路径下经历了m次的反射，则可划分为m+1段路径分段，把LOS 传播和 NLOS 传播的路径用分段路径来表示:

(7)

式中,l为LOS 传播距离，l′为NLOS 传播距离。

(8)

式中,Δd为地下停车场规律性NLOS 时延带来的测距误差。可以看出，误差与反射的次数有关。地下停车场障碍物的分布具有规律性，随着距离的增加障碍物数量增加，反射的次数也就增多，所以，随着距离的增加，式(8) 表示的地下停车场的NLOS 传播距离增量也会随着反射次数的增多而增大。因此，地下停车场NLOS 时延误差变化也相应地具有规律性。

本系统基于TOA测距技术，在含有LoRa芯片的模块上进行实现。在测得的数据中，包含参考NLOS延时模型建模的规律性NLOS时延、车辆等突发因素造成的随机NLOS时延和设备本身测量带来的误差。表达式可表示为:

d′=c(tTOA+tF+tR+tN)

(9)

式中，tTOA为信号LOS环境下的传输时间，tF为地下停车场的规律性时延，tR为地下停车场的突发时延，tN为设备自身的测量误差。通过均值滤波的方法可以对突发性时延误差滤除。

根据NLOS时延参考模型的NLOS时延扩展式(3)，地下停车场的规律性NLOS时延可视为服从相同的分布规律。使用的设备模块在进行TOA测距时自身的也会产生一部分误差，可视为固定值，假设为，因此，假设有下式成立。

d′=d+ctN+cTτdεξ

(10)

式中，c为光速，d′为测量值，d为与之对应的实际值，假定q=ctN，地下停车场NLOS时延系数p=cTτξ,因此式(10)化为:

d′=d+q+pdε

(11)

在实际使用中，根据测量值去估计实际值时，可近似的用式(12)代替式(11)来求解测量的实际值。

d=d′ +q+pd′ε

(12)

地下停车场的NLOS时延系数P、指数和设备模块自身处理误差q为未知量。在没有随机因素影响的情况下，对地下停车场任意的n点进行标定位置的测量采样，如对k个位置进行测量，测量值分别为d1′、d2′…dk′，对应的实际值为d1、d2…dk，可以依据这k组测量值与实际值建立起包含未知数q、p和ε的k(k-1)(k-2)/6组方程组，求解各个方程组，依据解集，求得具有最小欧式距离的一组数值作为对地下停车场规律性NLOS时延参数p和和设备自身测量误差q的拟合值。依据参数的拟合值，确定拟合函数，将上述均值滤波后的测距值带入拟合函数，求出对规律性NLOS时延和节点模块自身处理误差抑制后的测距值，用于下面所描述的三点定位算法，求得移动标签节点的位置坐标。

对本系统所采用对规律性NLOS时延和节点模块自身处理误差抑制的参数拟合的方法，在实验楼下地下停车场进行测试，采集了30组数据进行参数拟合，求得拟合函数如式(13)所示：

d=d′ + 0.827-0.247d′0.523

(13)

在地下停车场进行距离测试，距离测试结果如表2所示。

从表2可看出，通过参数拟合的方法，对滤波后的测距数值进行处理，可以很好地对规律性NLOS时延和标签模块自身处理误差进行抑制，测距误差在0.5 m左右，能够满足系统定位的要求。

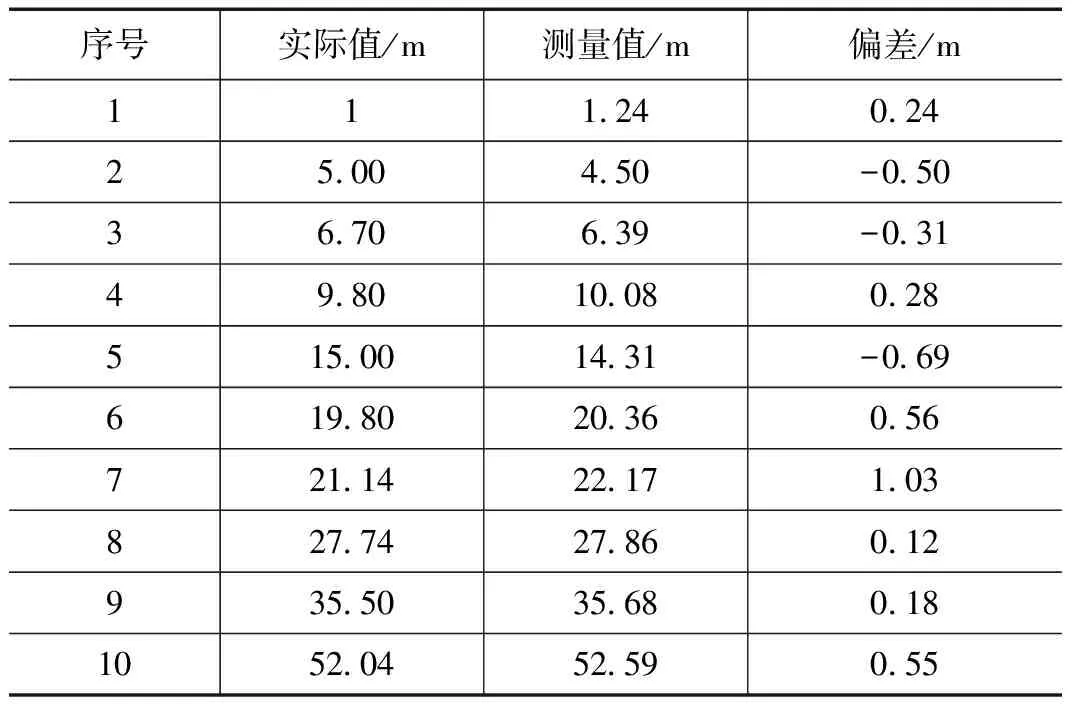
表2 标签节点与锚节点测距结果

3 定位实现

3.1 优化的三边定位算法

三边定位法的原理[12]如图3所示，以三个锚节点A、B、C为圆心，A、B、C三点的坐标分别为(Xa,Ya)、(Xb,Yb)、(Xc,Yc)，以移动标签到三个锚节点的TOA测距值da、db、dc为半径分别画圆，在TOA测距比较精准的情况下，这三个圆周相交于一点O，交点O即为移动标签的位置。假设交点O，坐标为(X,Y)。

图3 三边定位法原理图

(14)

通过TOA测距得到测距值距离da、db和dc，带入式(14)，可以计算出被测量点O的位置坐标(X,Y)。

但是，在实际进行TOA测距时，由于不能对NLOS时延进行完全抑制，实际的测量值并不能达到理想情况，由于噪声存在，从而导致上面的三个圆未必刚好交于一点，从而导致式(14)无解，因此,无法求解出移动标签坐标。

为弥补典型三边定位算法的不足之处，本文结合具体工程实践，提出了一种估计方法，与典型三边定位算法相结合，当上面的三个圆不交于一点时，对移动标签位置进行估计，作为当前移动标签节点位置坐标的最优解。具体方法如下：

图4 优化的三边定位算法原理图

1)基于距离的定位算法对测距的精度要求较高，在进行定位实现时，使用通过上面方法对NLOS时延进行滤波抑制过的TOA测距值。以锚节点为圆心，以与之相对应的TOA测距值为半径画圆，可以画出三个圆，任意两个圆之间只存在相切、相交和相离三种情况。

2)当两圆有交点时，当有两个交点时，选取距离第三个圆的圆心距离比较近的为估计点，如图4所示，A、C两圆相交于两点，选取O1作为估计点。当两圆相切时，取两圆的切点作为估计点。

3)当两圆相离时，以图4中A、B两圆为例，估计点在线段AB上，且满足线段长度|AO2|:|BO2|=R1:R2，可求出估计点O2。

4)通过以上方式可以得出三个估计点O1(XAC,YAC)、O2(XAB,YAB)和O3(XBC,YBC)，则移动标签节点的实际定位坐标为O(X,Y),其中:

(15)

通过以上步骤可以得到标签节点坐标。对三边定位算法进行优化，避免了无解的情况，该定位算法有较强的适应性，并且，还可以在一定程度上抵消测距噪声，提高定位精度。

3.2 节点模块软件实现

标签节点在随着驾驶者驾驶的车辆驶入地下停车场时，不断以广播的形式与周围锚节点通信，锚节点收到广播后进行回复，标签节点启动测距定位。具体实现流程如图5所示。

图5 标签节点和锚节点工作流程图

如图5所示，锚节点和标签节点在工作之前先对LoRa模块进行初始化配置，在配置SX1280时，需要对载波频率扩频因子、CRC校验方式、信号带宽 、发送功率以及数据包结构进行设置。

同时，在进行TOA测距之前，先对接收强度进行判断，选择接收信号强度比较好的，通信质量比较高的锚节点进行测距定位，进一步提高了定位的可靠性和精度。

4 系统功能测试

本系统采用COT-MV1 2.4G标准模组，如图6所示，内置LoRaSX1280芯片。对通信参数进行如下配置：扩频因子为7、编码率为4/5、 信道中心频率为2402 MHz。

图6 COT-MV1LoRa模组图

以广西民族大学信息科学与工程学院楼下的小型地下停车场为测试场景，进行定位实现，地下停车场总面积为49.00 m×10.60 m,停车位个数为16，整体布局如图7、8所示。

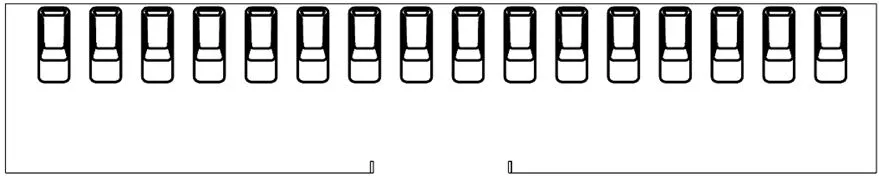
图7 地下停车场示意图

图8 地下停车场实验环境图

标签节点随着车辆从出入口道路到停车位移动，在进行锚节点布局时，要保证能完全覆盖整个地下停车场，从而能对移动标签节点的任意位置实时定位。定位精度受锚节点的布局影响很大，合理的锚节点布局，不仅能提高定位精度，还能节约设备成本。

对实验楼下地下车库进行锚节点布局时，可以采用图9所示的方法布置，布置了6个锚节点，都布置在了地下停车场的边界处，保证了移动标签在地下停车场的任意位置都能进行有效定位。对三边定位算法进行理论分析和实践检验发现，定位精度受测距半径影响较大，当测距半径较大时，即使测距精度较高，定位精度也会下降。在进行锚节点布局时，使得任意两个相邻的锚节点的距离最大为24.50 m，使得在进行移动标签节点和锚节点测距时，结果不至于过大，影响定位精度。

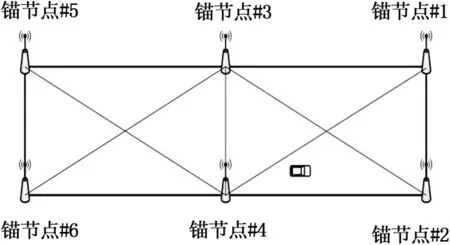
图9 锚节点布局图

对改进的三边定位算法进行分析，反复实地测试，发现标签节点在选取的三个锚节点组成的三角形内部时，定位的准确性较高，测距误差对定位精度影响较小。移动标签节点依据信号接收信号强度选取三个距离比较近的锚节点作为定位参考点，以保证标签节点在选中的三个锚节点组成三角形的内部。

人员携带COT-MV1 2.4 G标准模组作为移动的标签节点，并且保持匀速移动来模拟车辆的行驶，在地下车库的任意位置移动，确保测试位置的随机性和全面性，能够准确反映定位系统的真实情况。按照图9所示的位置布置6个锚节点，6个锚节点的坐标分别为(0,0)、(0,10.60)、(24.50,0)、(24.50,10.60)、(49.00,0)、(49.00,10.60)。

在对定位进行误差分析时，引入如下公式：

(16)

式中，Δ为定位误差，(x,y)为标签节点的定位坐标，(x1,y1)为标签节点的真实坐标。

定位测试结果如表3所示。

表3 标签节点定位结果

针对地下停车场特殊的环境，结合NLOS时延参考模型，使用上述方法，对TOA测距的NLOS时延进行抑制，得到精确度相对较高的TOA测距值，使用上述优化的三边定位算法来实现定位。从表3可以看出，定位误差在1 m之内，可以满足对车辆定位的基本要求。

5 结束语

本文将LoRa技术应用在地下停车场定位系统中，充分利用LoRa技术低成本、低功耗、低复杂度的优势。对地下停车场的NLOS时延进行分析，通过改进的均值滤波算法和参数拟合的方法对TOA测距的LNOS时延和设备自身测量误差进行抑制。对常用的三边定位算法进行分析，总结算法的优缺点，对算法进行了优化，在不增加任何硬件成本的前提下，能够减小环境噪声带来的测量误差对定位精度的影响。在实际的地下停车场验证了定位系统的可行性，定位精度在1 m之内，实验结果表明，该系统具有一定的实际应用价值。