基于二代小波算法的数字全息显微成像自动对焦方法
2019-03-05,,,,
, ,,,
(浙江工业大学 信息工程学院,杭州 310023)
0 引言
全息术由Gabor在1948年首次提出,1967年Goodman和Lawrence提出采用计算机重建全息图的思想。经过多年的发展,数字全息术的特殊优点使其在最近几年成为国际研究的重要领域之一[1]。目前,数字全息术已广泛应用于各个方面,如微小距离计量[3-4]、微生物研究[5]、粒子分析[6]、存储、加密等,其中,数字全息显微成像技术也成为数字全息术[7]的重要应用之一。
最佳重建距离是获取最优全息重建图像的重要参数之一,传统手动输入重建距离的方式不仅效率低,而且因为难以获得准确的重建距离而导致不能获取最佳重建图像。近些年来,数字全息显微自动对焦技术已获得广泛关注,基于图像清晰度评价函数的数字全息显微对焦技术是目前应用的主要对焦技术之一。图像清晰度评价函数大致可分为以下几类:基于空间特征的评价函数,如灰度方差法、拉普拉斯算子等;基于频域特征的评价函数,如傅里叶变换、离散余弦变换等;基于信息熵的评价函数等[8]。然而这些传统算法对于数字全息图的评价存在很多问题,如全息图的噪点影响等可能让算法失效,无法准确找到最佳重建点。因此,本文提出一种基于二代小波[9]的数字全息显微成像自动对焦方法,利用此方法可以自动寻找最佳对焦点,获取全息图的最优重建效果。
近年来,嵌入式产品由于体积小和使用方便等原因被广泛使用,且部分嵌入式产品已被应用于国防、工业、通信等多个领域[10]。因此,数字全息显微成像技术的便携化也是目前数字全息显微技术发展的重要目标之一。如何将基于PC平台的传统算法移植到嵌入式平台,同时具有较好的重建速度也是目前研究的主要方向之一。因此,本文提出一种基于OPENCV和FFTW库的角谱算法,结合同轴全息光路和嵌入式处理平台实现嵌入式平台上的数字全息显微重建。
1 系统结构及原理
数字全息显微系统由硬件和软件两大部分组成,其中硬件部分主要完成全息图的采集、计算、结果显示、用户交互等工作;软件部分则利用基于OPENCV和FFTW库的角谱算法结合二代小波图像评价算法对全息图进行全息重建和图像评价处理,实现全息图的自动对焦重建。
1.1 系统结构
全息图是由参考光与物光干涉而产生,因此全息图中包含了物体的全部信息。全息图由图像传感器记录,从而获取全息图的数据。如图1所示,该系统主要包括三个部分:光路采集、计算处理和显示交互。
数字全息光路包括同轴与离轴两种,相比于离轴全息,同轴全息因为具有光路更加简单,能够较好的微型化等优点,所以更加适用于数字全息显微技术的便携化应用。因此,本系统选择采用同轴全息光路,如图2所示,同轴全息光路主要是利用光源的相干性,当相干光透过物体时,一部分直接透过物体为参考光,另一部分在物体上发生衍射形成物光,两种光发生干涉形成全息图,从而被图像传感器CMOS记录,本系统采用650nm部分相干红色LED作为光源,利用200um微孔增加其相干性,为了获取更加清晰的图像,采用1.4um像元尺寸的CMOS传感器作为图像传感器。
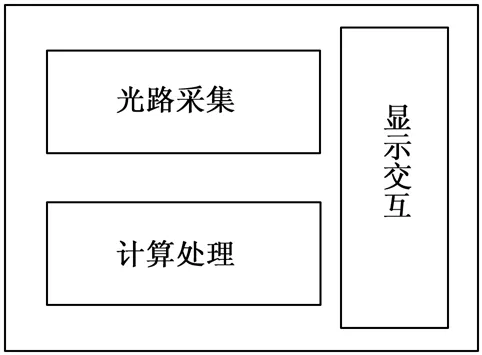
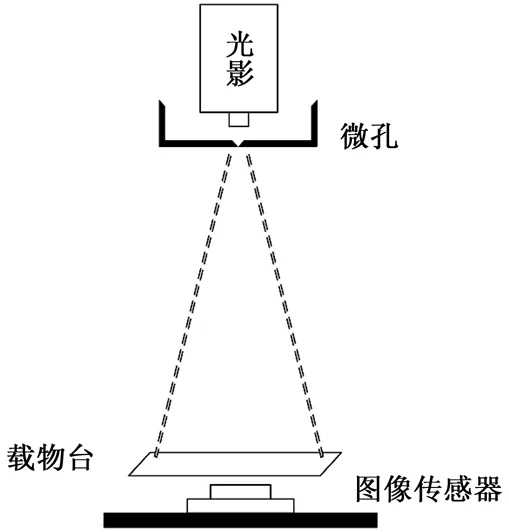
图1 系统结构图
图2 同轴光路图
在计算处理部分采用TI公司的AM335X处理器作为处理核心,该处理器最高主频为1G赫兹,同时配合Linux嵌入式操作系统完成整个处理过程。显示交互部分采用7寸液晶屏和触摸屏配合,通过LCD总线和I2C总线实现数据与AM335X的通信,完成整个采集、处理和显示过程。整体装置框架如图3所示。
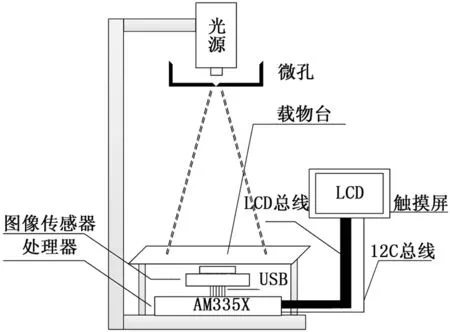
图3 自制数字全息显微系统框架图
图像传感器获取到全息图后利用USB串行数据总线将数据传输给嵌入式处理器AM335X,AM335X获取到全息图数据后利用OPENCV和FFTW配合优化后的角谱算法对全息图进行重建,然后利用图像质量评价函数对重建后的图像进行评价,找到最佳重建点,最后将最佳重建图像通过LCD总线输出到LCD显示屏进行显示。
1.2 全息原理
全息技术是利用相干光的特性,结合图4所示,一部分相干光照射待记录的物体形成物光波,另一束直接照射在干板上形成参考波,参考波与物光波在图像传感器上进行干涉,从而形成包含物体振幅和相位信息的全息图。此时,由图像传感器记录,并保存物体的原本全部信息。

图4 全息原理示意图
数字全息重建就是利用计算机模拟光路,还原物体原始信息的方法[11-12],由傅里叶逆变换可知光场与其角谱[13-14]之间的关系为:
(1)
即F(fx,fy)为光场f(x,y)的角谱,由此可得:
(2)
将F(fx,fy)用方向余弦表示:
(3)
根据标量波动方程,任一平面光场可看做无数组传播方向不同,幅值不同的平面波叠加而成。因此得到角谱之间的关系:
(4)
由上面的式子可知,角谱与其光场的关系为傅里叶变换的关系,则角谱重建算法得到的再现像光场的复振幅分布为:
U(x,y)=F-1{F[U0(x,y)]GAS(fx,fy)}
(5)
其中:U0(x,y)为实际记录时的全息图,GAS(fx,fy)为计算机需要模拟的传递函数,公式为:
(6)

从式(5)、(6)可知,数字全息显微重建需要的输入参数包括:图像传感器记录的全息图U0(x,y),参考波的波长,图像传感器像素尺寸和,重建距离。
重建距离代表物体实际距离图像传感器的距离,因此只有当重建距离等于实际重建距离时,才会得到最清晰的重建像,但由于这个距离一般小于1 mm,难以测量,实际重建过程中难以获得。因此,本文提出利用图像质量评价函数完成数字全息显微自动对焦,从而获取最佳重建距离以及重建物像的方法。
2 数字全息显微自动对焦方法
鉴于重建距离Z值难以获得的情况,本文提出基于二代小波算法的数字全息显微成像自动对焦方法。该方法是利用图像质量评价函数对重建后的全息图进行评价,根据评价结果进行最佳重建距离Z值的确定,从而获得最佳重建效果。经过对比几个传统图像质量评价方法,实验证明二代小波图像质量评价方法更加适用于数字全息显微重建后的图像质量评价,能够准确获取最佳重建点。
2.1 常用图像质量评价函数
图像质量评价函数是通过对图像的像素之间的关系进行相关计算,从而判断该图片质量的好坏。当图像清晰时,图像细节更加丰富,在时域的表现为像素之间的特征值变化较大,在频域的表现为高频分量更多,经过大量的研究,国内外学者提出了许多清晰度评价方法,其中比较经典的有灰度方差法、Laplacian函数、Tenengrad能量梯度法等。
2.1.1 灰度方差法
图像越清晰,边缘越明显,对应的灰度方差值也就越大,因此,图像的清晰度可用灰度方差法来表示,灰度方差公式如下:
(7)
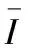
2.1.2 Laplacian函数
Laplacian函数采用二阶微分的Laplacian算子与图像进行卷积,然后取结果的梯度平方和用来评价图像清晰度,其表达式为:
(8)
其中:G(x,y)=f(x,y)⊗L,L为卷积核。
2.1.3 Tenengrad函数
Tenengrad函数是一种基于梯度的图像评价函数,图像越清晰,具有更加尖锐的边缘,因而具有更大的梯度函数值。Tenengrad函数是使用Sobel算子提水平和垂直方向的梯度值进行评价,其表达式为:
(9)
其中:Gx、Gy为Sobel算子的卷积核。
2.2 二代小波
二代小波是由Sweldens[15]等人在1994年提出,当时其提出一种在时域中构建第二代小波变换的方法。二代小波的显著优点是提高了小波变换的速度,其不需要傅里叶变换,放弃了二进平移和伸缩的条件,速度约为传统小波变换的2倍,同时还具有第一代小波的全部优点。此外,其整个运算不需要额外的辅助存储内存,非常适用嵌入式平台内存资源缺乏的情况。
2.2.1 二代小波原理
二代小波通过三个步骤来实现高频与低频的分离,分别为分裂、预测和更新[16]。
步骤1:分裂(split)
分裂过程是将原始图像Sj分解成奇数集和偶数集两个部分,奇数集Sj,2l+1为原始图像奇数位置的值的集合,偶数集Sj,2l为原始图像偶数位置的值的集合,如下式所示:
Sj=(偶数集,奇数集)=(Sj,2l,Sj,2l+1)
(10)
步骤2:预测(predict)
预测部分是利用数据间的相关性用偶数部分的值去预测奇数部分的值,主要过程为利用预测算子p结合偶数集中的值去预测奇数集中的值,然后对比奇数集中的值与预测值之间的差值,得到差值dj-1,该差值就是原始信号经过小波变换后的高频部分,如下式所示:
dj-1=sj,2l+1-p(sj,2l)
(11)
其中:dj-1为预测差值,对应高频部分,p为预测算子。
步骤3:更新(update)
采用更新计算是因为经过分裂产生的Sj,2l的一部分整体性质与原始图像有差异,需要对其进行更新运算,更新过程为将更新算子U作用于预测部分得到的残差值dj-1上,从而生成一个与原始图像相同的子集cj-1,如下式所示:
cj-1=Sj,2l-U(dj-1)
(12)
其中:cj-1对应低频部分,U为更新算子。
若想实现多级二代小波变换,则只需对cj-1重复上面的分裂、预测和更新三个步骤即可。对原始图像进行二级小波分解如图5所示。

图5 二代小波变换示意图
由此可知,二代小波可对原始图像分解为4部分:1个低频部分LLn和3个高频部分LHn,HLn,HHn,其中LLn是其经过n级变换后的低频分量,LHn、HLn、HHn分别为其经过n级变换后的垂直、水平和对角线方向上的高频分量。
2.2.2 基于二代小波的图像质量评价函数
用二代小波变换结合图像的能量函数来评价图像的清晰度,当图像清晰时,二代小波变换后的高频部分能量最大,随着图像的模糊,能量逐渐向低频部分分布,此时高频部分能量减少。因此,根据二代小波变换后的高频部分与低频部分的能量可以评价图像清晰度,且在全息图具有部分噪点的特性基础上提出了综合低频与高频部分的清晰度评价函数,如下式所示:
(13)
其中:HLn,LHn,HHn为n级二代小波变换后的高频部分,LLn为n级二代小波变换后的低频部分。
3 数字全息显微软件系统设计
该系统硬件部分主要由三部分组成,软件处理部分大致可分为6部分,如图6所示,当图像传感器获取到全息图后,利用USB串行数据总线传输给嵌入式平台AM335X进行图像预处理、全息重建、二代小波分解和图像质量评价,重复以上过程,不断扫描不同重建距离Z值,得到不同重建距离Z对应的重建结果图像评价值,然后找到最佳的评价值,即找到最佳重建距离,最后输出最佳重建结果。主要流程如图6所示。

图6 软件流程图
3.1 图像预处理
由于以图像传感器最大分辨率获取全息图,因此图片信息较大,而嵌入式平台处理能力相对较弱,因此采用中心部分320x240大小RIO提取的方法裁剪图片,找到感兴趣区域,同时减少计算量,预处理过程如图7所示。

图7 图像预处理
3.2 全息重建
利用全息重建算法对预处理后的全息图进行全息重建,得到重建后的物体图像。对照全息原理,首先利用傅里叶变换将全息图转换到频域,得到全息图对应的角谱,然后经过相移,将零频点移动到频谱中间,再利用角谱之间的关系乘以传递函数GAS,得到对应重建距离的频谱,最后再次相移后,利用傅里叶反变换得到重建后的图像。整体重建过程如图8所示。

图8 全息重建过程
3.3 基于图像评价的自动对焦
当得到重建的图像后,再利用二代小波对图像进行二级变换处理,提取全息图的高频与低频部分,结合二代小波图像质量评价函数对重建图像进行评价,二代小波分解过程如图9所示。
如图9所示,经过二级变换得到对应的高频与低频部分,分别求得高频与低频部分的能量值,并带入二代小波质量评价函数式(13)求得对应的评价结果。重复扫描重建区间内的不同重建距离,得到对应的图像评价结果,找到最佳图像质量评价值,即找到最佳对焦点,从而获取最佳重建结果,完成自动对焦。
4 实验结果与分析
4.1 重建速度
基于数字全息显微技术便携化的要求,本文将基于传统PC的数字全息显微重建算法应用于嵌入式平台,且为了能够实现实时重建,需要对传统算法进行改进,因此,本文采用OPENCV和FFTW库结合的形式去提高算法速度。前面提到,整个重建过程主要包括两部分:1)传递函数;2)角谱重建。因此,分别对这两部分进行测试,并得到该算法在AM335X平台平均实际运行速度如表1所示。
由测试结果可知,当嵌入式主板主频在1 GHz时,该算法计算时间大约为0.6 s,本文采用OPENCV配合FFTW库的方式实现的角谱算法满足在嵌入式平台实时重建的要求。
4.2 重建精度
重建精度是数字全息显微系统的重要指标之一,因此,采用USAF1951标准分辨率板对该系统的重建精度进行测试,如图10所示。

图10 分辨率板重建
如图10可知,该系统对分辨率板全息图重建后,最大可分辨第7组的第2位,查分辨率表得,该系统的重建精度为3.48 μm,可观察3.48 μm的微小物体。
4.3 自动对焦准确率
由于数字全息显微重建算法最佳重建距离难以获得,本文提出了一种基于二代小波方法和角谱算法结合的数字全息显微成像自动对焦方法。为了对比其他图像评价算法,需要将各算法对全息图重建后得到的结果进行评价,将得到的评价值进行归一化处理,得到各评价算法对于各重建距离的图像质量评价曲线。如图11所示,得到各图像评价函数对一张分辨率板全息图重建距离为0 mm到1 mm区间进行自动对焦时的图像质量评价曲线,该分辨率板实际对焦距离(图中△处)为0.59 mm。由图中可知,拉普拉斯算子和灰度能量梯度函数得到的评价曲线相对杂乱,对焦点误差较大,而二代小波函数和灰度方差法的到的评价函数明显得到最佳对焦点。
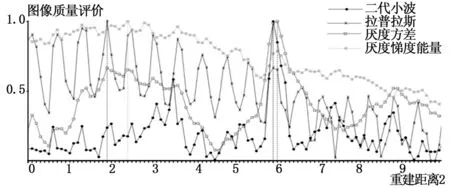
图11 图像质量评价函数归一化
根据各评价曲线总结如表2所示。
表中峰值性用来描述最佳对焦点相对其附近重建点的差值,由图中可知,二代小波与灰度方差法相对峰值性较好,Laplacian(拉普拉斯)算子和Tenengrad(灰度梯度能

表2 图像质量评价函数自动对焦结果对比 μm
量)函数评价曲线则相对杂乱,峰值性较差,无法观察到分辨率板刻度,分辨率大于500 μm,不适用于全息图的自动对焦。二代小波准确对焦,且峰值性最好,分辨率达到最佳为3.48 μm,灰度方差法则有些许误差。因此,二代小波算法自动对焦效果最好。为了检验此数字全息显微自动对焦的准确率,我们随机选取5副分辨率板全息图进行自动对焦测试,并将结果与实际重建点进行对比,结果如表3所示:
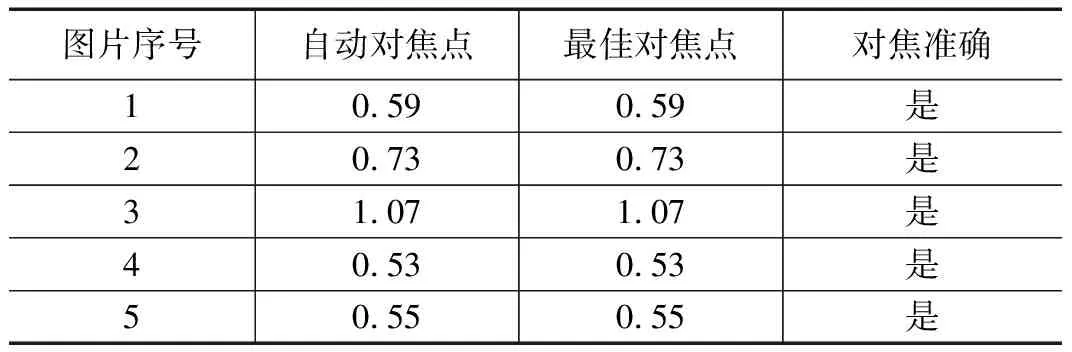
表3 自动对焦点与最佳对焦点比较 mm
是进一步验证自动对焦准确率,利用该系统采集20副分辨率板全息图进行验证,对焦准确为18张,对焦准确率为90%。本装置基于二代小波的数字全息显微自动对焦系统对全息图自动重建的效果如图12所示。

图12 全息自动对焦重建图
实验结果表明,本文提出的基于二代小波的数字全息显微自动对焦方法具有较好的准确率,自动对焦准确率达90%以上,能够解决传统算法难以获取最佳重建距离的问题。
5 结束语
针对目前数字全息显微重建技术依赖传统PC平台的问题,本文采用OPENCV配合FFTW库实现角谱重建算法,实现嵌入式平台的快速重建,重建速度大约为0.6 s,系统的重建精度达到3.48 μm,对数字全息显微成像技术的便携化发展具有重要意义。针对传统数字全息显微重建算法需要
手动输入重建距离且重建距离获取困难的问题,本文提出基于二代小波算法的数字全息显微成像自动对焦方法,用全息图自动寻找最佳重建点,自动对焦准确率为90%以上,解决了传统重建算法难以获取重建距离的问题。
