一种遥感卫星动量轮容错控制的方法研究
2019-03-05,,,,
,,, ,
(1.中国电子科技集团 第五十四研究所,石家庄 050000; 2.哈尔滨工业大学 航天学院,哈尔滨 150001)
0 引言
低轨遥感卫星由于任务需求,往往需要在失重、高低温和强辐射的恶劣环境中频繁的机动,暴露出的在轨问题愈发显著。文献[1]记录了1988~2014年的遥感卫星在轨故障数据,统计发现低轨遥感卫星由于应用广泛、在轨数量多等原因,其故障频率远高于高轨遥感卫星,约为高轨遥感卫星的6倍。其中,控制分系统37.5%的故障频率为各分系统中故障最高的。控制分系统的失效将严重影响卫星的在轨运行,5%的控制分系统的在轨故障为致命故障,高于其他分系统的致命故障占比。而动量轮由于使用寿命长、控制精度高等优点,在控制分系统中是十分重要的组成部分。然而,对于长时间在轨的卫星来说,高速旋转的动量轮的寿命和可靠性受到限制,一旦动量轮发生故障,卫星将因为姿态不稳定而无法实现对地定向、对日定向等基础设置,即使其他部件正常,也会对原有任务造成巨大影响。综上所述,对于低轨遥感卫星,动量轮是其卫星控制分系统的重要组成部分,也是其卫星正常运行的基本保障。因此,针对低轨遥感卫星进行动量轮容错控制研究是很有必要的。
到目前为止,针对卫星动量轮进行容错控制研究的主要困难,还是其模型高度非线性和系统故障非线性导致的非线性控制问题。针对这两方面问题,卫星动量轮控制方面的研究中模糊PID控制在解决模型非线性问题上表现突出,文献[2-3]设计了自适应调节参数、有出色的鲁棒性的三轴稳定零动量轮模糊PID控制器,调节时间减小明显;航天器容错控制方面,相似思想方法的控制理论也有很多,例如自适应控制方法,自适应控制的核心在于不需要知道干扰和不确定性的界,而是由自适应学习策略自动确定时变的控制增益[4-5]。文献[6]针对航天器执行机构(动量轮)故障的姿态控制问题,提出基于线性变参数(LPV)系统的鲁棒变增益PID容错控制。文献[7]针对航天器执行机构发生失效故障且故障信息未知的容错控制问题,提出了基于自适应滑模控制器的容错控制策略。
本文建立姿态控制系统高精仿真模型,应用卡尔曼滤除敏感器模型产生的噪声,实现对姿态控制系统的精准监测。而后根据对模型的分析和调试规律总结,设计模糊PID容错控制器,并与传统PID容错控制的效果进行对比,经仿真验证可知,相较之下该模糊PID容错控制器的控制精度、能源节约都有明显提升。
1 模型建立
1.1 姿态控制系统模型建立
本文的故障诊断及容错控制系统,针对由三个上述零动量轮组成的姿态控制系统而设计的。故而采用欧拉角描述下的航天器姿态运动方程,并基于小欧拉角运动将方程线性化简化:

(1)
其中:
I=diag(I1,I2,I3)
(2)
(3)
(4)
其中:ω=[ω1,ω2,ω3]T表示航天器相对于惯性坐标系的角速度在本体系中的表示,而Θ=[φ,θ,ψ]T表示航天器姿态角矢量,而u=[τ1,τ2,τ3]T为由动量轮系统产生的作用于航天器本体上的总控制力矩,Ii(i= 1,2,3) 表示航天器整体的三个主转动惯量,而d=[d1,d2,d3]T则为作用于航天器上的外部干扰力矩。
又由于故障程度组成对角阵ρ(t)=diag([ρ1(t),ρ2(t),ρ3(t)]T)为故障程度矩阵,因此可以改写输出力矩u=[τ1,τ2,τ3]T为:
u=ρ(t)u=Up(t)
(5)
其中:U=diag([τ1,τ2,τ3]T),p(t)=[ρ1(t),ρ2(t),ρ3(t)]T。此时,航天器姿态运动方程(1-13)在部分失效故障发生时可改写成如下形式:
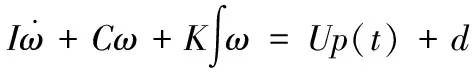
(6)
1.2 高精度动量轮仿真模型建立
动量轮是卫星姿态控制系统中普遍采用的一种执行机构,主要分为偏置动量轮与零动量轮(也称反作用飞轮)两种。由于零动量轮组成的三轴稳定控制系统,比偏置动量轮控制系统有更稳定、精确的性能。并且随着对卫星定位精度要求越来越高,零动量轮三轴稳定姿态控制系统的应用越来越广泛。所以,本文选取零动量轮作为研究对象。
1.2.1 动量轮分模块详细介绍
在了解动量轮最基本的工作原理之后,本文选取广泛采用的ITHACO[13]动量轮模型进行分模块详细介绍,如图1所示。

图1 ITHACO动量轮模型基本框图
1)控制力矩模块:控制力矩模块可以分为两部分,第一部分是控制电压驱动,本质上是一个增益为Gd的电压控制电流源。第二部分是控制电流驱动,本质上是增益为Kt的电流驱动的力矩产生模块。
2)角速度限幅:为了防止飞轮达到不安全的速度,速度限制器电路是采用动量轮角速度模拟测试电路,并提供高增益负反馈Ks。当转矩命令超过一定阈值(或操作过程中超过)时,产生负反馈抑制转速的增大,同时预警。
3)电动势补偿:在低总线电压条件下,在高速旋转的电动机可能由于反电势增加Ke,而消除一定的控制电压,导致减少了转矩。一旦反电势增加,总线的脉宽调制将是饱和的。从干扰的角度来看,还应该指出的是,此时的电动机转矩将直接耦合到总线电压,和任何总线电压的波动也产生力矩干扰。
电动势补偿是轻度耦合电压降功耗的输入滤波器。这个电压降是总线电流、总线过滤器输入电阻,RIN的乘积。总线电流功率消耗依赖于总线电压、电机电流、车轮速度和总线电压。
根据上述的理论可以得到一系列相关的公式,在这里不一一介绍,总之电动势补偿模块是针对电机高速运转时产生的反电动势,通过对控制信号反馈,进行补偿的模块。
4)摩擦模型:动量轮上的摩擦力矩,通常被称为阻力矩,可以被分为库伦摩擦和粘性摩擦。库伦摩擦力即为我们最为熟悉的静摩擦和滑动摩擦的统称,与作用在摩擦面上的正压力成正比,而与接触面积无关。粘性摩擦则与速度和温度有关。
粘性摩擦与润滑密切相关,且对温度十分敏感,但在本文中,并没有为动量轮粘性摩擦加入温度的变量关系。原因虽然可以得到温度和粘性摩擦的关系,但是该模型没有办法得到温度的相关信息,本文就选取了一个温度的中位数进行替代,虽然有误差但影响不大。所以,下一步的模型完善中,研究的重点将是如何建立温度与动量轮转速、电机电流等变量之间的关系。
2 常见动量轮故障分析
首先,根据初步的文献整理可知,动量轮常见故障及故障特点如表1所示。
动量轮常见故障模式的数学模型如下:
1)卡死故障:
(7)
式中,τ动量轮实际输出力矩(N *m);τc动量轮理论输出力矩(N *m);w为动量轮飞轮的角速度(rad/ s);tp为动量轮故障发生时刻(s)。

表1 动量轮常见故障模式
(2)空转故障
(8)
(3)摩擦力矩增大
(9)
式中,τfe为额外的动量轮故障摩擦力矩( N *m )。
(4)跳变故障
(10)
(5)增益下降
(11)
式中,ρ(t)为故障程度,即动量轮故障增益。
根据上述故障表现和数学模型进行分析:
1)首先可以很容易看出,卡死故障和空转故障,在故障程度上无疑是最严重的,当这类故障一旦发生,除了重启、切换这些保守而传统的措施,基本没有容错控制的余度。这类故障的相关研究方向应该更多地着眼于故障早期预测,所以本文并不对此进行深入研究。
2)其次是摩擦力矩增大,由于摩擦分为两部分,即库仑摩擦和粘性摩擦。库伦摩擦主要与表面受力有关,所以当库伦摩擦力矩增大时,往往是结构不稳等不可逆故障所导致,所以讨论的余度不大。而粘性摩擦,则与飞轮的转速、轴承的稳定和润滑效果等因素相关,所以当粘性摩擦力矩增大时,即使是由于润滑剂挥发等不可逆故障所引起的,也可以通过调整飞轮转速,从而达到容错的效果。而如果是由于动量轮轴承温度过高、轮盘角速度过大,则是直接与动量轮转速相关,自然可以通过动量轮转速进行容错控制。所以,可以得出结论,针对摩擦力矩增大的故障,可以进行故障诊断及容错控制设计。但是,由于本文所选取的动量轮模型中,不涉及动量轮轴承温度的信息,所以并不针对动量轮摩擦力矩增大的故障模式进行研究。
3)而后的是跳变故障,表现形式为冲击型故障,由于这类故障时间短且随机、幅值不定,所以对其的容错控制类似于有一定初值的姿态稳定问题。
4)最后增益下降的故障模式,其故障表现形式与摩擦力矩增大的表现形式十分类似,其故障原因往往是控制电路老化等引起的控制电压增益改变,导致同等控制电压驱动得到的输出力矩低于预期力矩。所以,可以通过改变控制电压对下降的增益进行补偿。
故而综上所述,本文最终选取增益下降故障作为研究对象,并结合动量轮高精模型的内部机理,得到具体的故障设置模型如下:
(12)
C为驱动电机故障、由于温度的变化,元器件老化等因素导致的力矩控制系数变化倍率,通常情况下C<1。
3 基于KF的模糊PID动量轮容错控制方法
3.1 卡尔曼滤波实现
目前卡尔曼滤波算法的理论日趋成熟,对于噪声具有鲁棒性,是一种广泛使用的故障诊断方法。目前大部分的卡尔曼滤波算法实现都基于线性模型,然而实际的动量轮是较为复杂的非线性系统,高精仿真模型中自然也包涵非线性项。具体实现时,考虑到时间层面的可行性,将数学模型线性化。具体内容如下:
建立基于单个动量轮仿真模型的状态空间模型如下:

(13)
对式(13)的非线性动量轮系统模型进行线性化近似,可以得到:

(14)
矩阵F写为:
式中,LA代表电机线圈电感;RA代表电机线圈电阻;Ψ代表电机的磁通量
对式(14)进行卡尔曼滤波设计,从而获得状态空间的估计方程。基于卡尔曼滤波五大基本方程的更新方程为:
(15)
更新的初值为:
(16)

3.2 模糊PID控制器设计
模糊PID控制器通过模糊化、知识库(数据库与规则库)、模糊推理和去模糊化这4个部分的互相作用,以控制变量作为输入,在不需要被控对象精确的数学模型的情况就可以实现对系统较为理想的控制。
3.2.1 输入输出及隶属度函数
根据卫星动量轮模型特性和姿态稳定的控制需求,选择角速度矢量偏差we和角度矢量σe作为控制输入,PID控制器Kp、Kd、Ki的调整量作为输出。根据卫星动量轮相关参数,经预实验确定输入部分we和σe的基本论域分别为[-0.04,0.04]和[-0.04,0.04]。模糊论域均选取[-1,1],并划分为{NB,NM,NS,ZO,PS,PM,PB}7个等级。比例因子均为K=0.04。对应的隶属度函数如图2所示。

图2 隶属度函数图
同理再确定输出部分,Kp的基本论域分别为[0,100],Kd的基本论域分别为[0,10],Ki的基本论域分别为[0,1],模糊论域选择[0,1],模糊子集也选择{NB,NM,NS,ZO,PS,PM,PB}。则比例因子Kp=0.01,Kd=0.1,Ki=1。对应的隶属度函数如图2所示。
3.2.2 模糊规则与模糊推理
模糊规则主要是根据工程人员或是专家的经验来总结并按照人的思维方式来进行语言表达的一种规则形式。下表是基于仿真调试总结的Kp、Kd、Ki增量的模糊规则。按照表1和表2在Matlab中的fuzzy工具箱逐条输入“If条件,Then结果”的语句形式的控制规则。选择最为常用并且易于用图形进行解释的Mamdani推理法作为模糊逻辑推理方法。

表2 比例系数ΔKp增量的模糊规则

表3 比例系数ΔKi增量的模糊规则
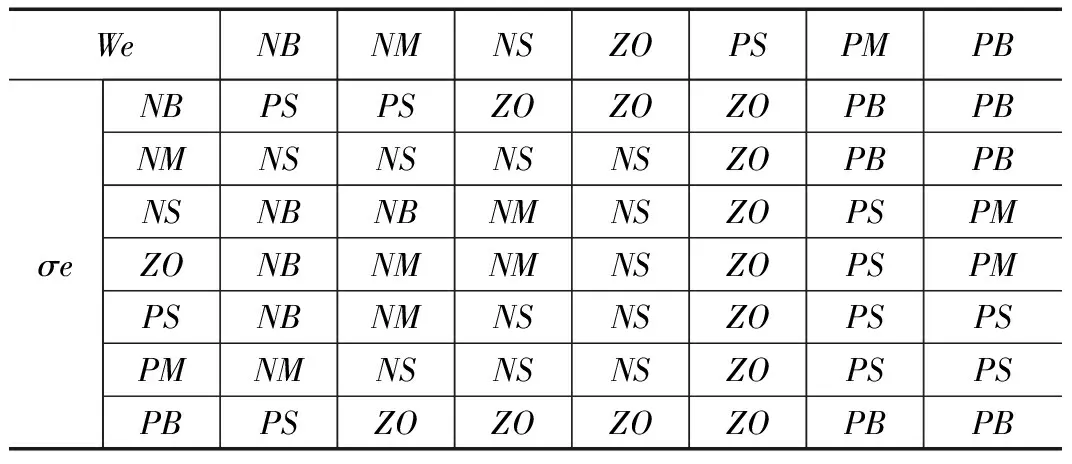
表4 比例系数ΔKd增量的模糊规则
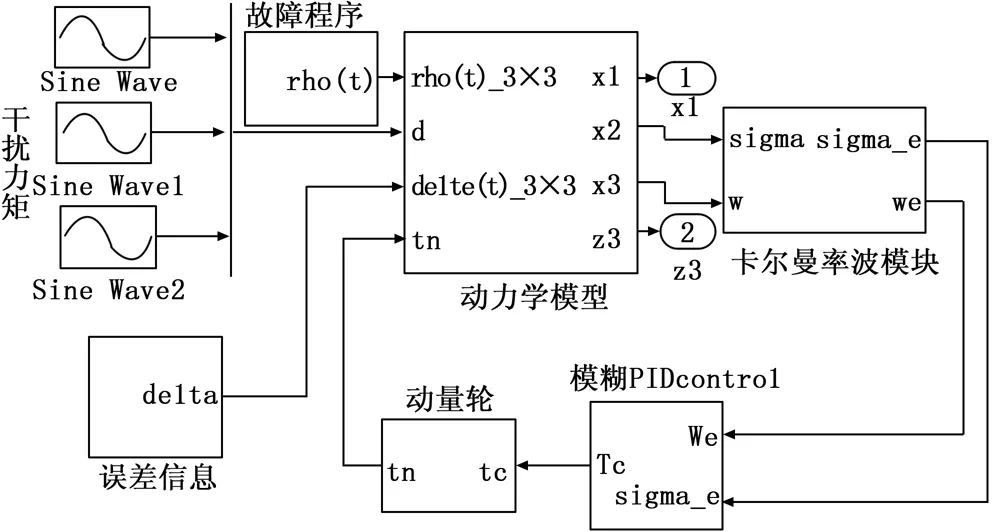
图3 模糊PID容错控制模块示意图
3.2.3 去模糊化
去模糊化的目的是将推理决策得到的模糊量回复为可用于系统进行控制的精确的数值。本文采用加权平均法作为去模糊化的方法。将Kp、Kd、Ki系数原始值分别与模糊推理得到的其对应的增量值相加,得到最终的Kp、Kd、Ki系数。从而实现了模糊控制对常规PID控制器系数的调整。综上,得到模糊PID容错控制器。
4 仿真结果及分析
针对设计的容错控制器进行仿真实验,验证其效果,并设置PID控制器作为仿真对照实验。参数设置如表5所示。

表5 仿真参数初值表
模糊控制器的增减量,基于PID容错控制器参数,作为对照。
PID仿真结果如图4~11所示。

图4 故障&干扰PID控制
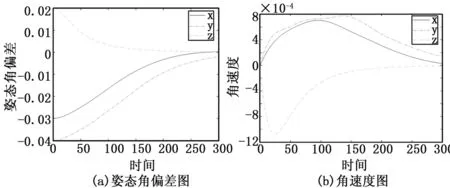
图5 故障&干扰模糊PID控制
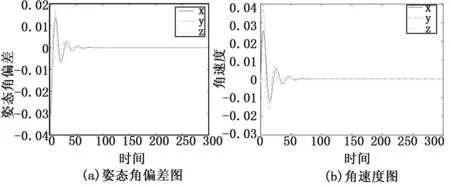
图6 无故障&干扰PID控制

图7 无故障&干扰模糊PID控制

图8 无故障&无干扰PID控制
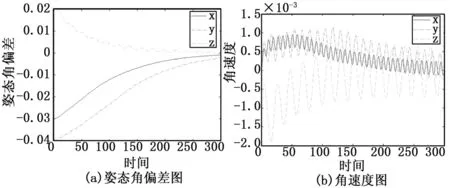
图9 无故障&无干扰模糊PID控制

图10 故障&无干扰PID控制

图11 故障&无干扰模糊PID控制
根据上述仿真结果分析可得,PID控制下x轴姿态角偏差第一次量约为初始偏差的70%,y轴姿态角偏差的超调量约为初始偏差的87.5%,z轴姿态角偏差的超调量约为初始偏差的30%,控制时间约为250 s,三个轴姿态角偏差
的稳态误差约为初始偏差的3.33%。三个轴角速度的量级为10-2,且在300 s后还有衰减中的角速度变化。
本发明提出的模糊PID控制下,无超调量,控制时间也约为250 s,稳态误差趋近于零,三个轴角速度的量级为10-4,且300 s后角速度趋近于零,相应的飞轮所需的控制力矩也小于传统PID控制,且在300 s后可以不需要控制力矩。可以得出结论,该模糊PID容错控制器的控制精度、能源节约都有明显提升。
5 结束语
本文的基本思路是先建立低轨遥感卫星动量轮故障模型,应用卡尔曼滤波算法进行噪声滤除,然后根据卡尔曼滤波的结果,设计模糊PID容错控制器。通过与传统PID容错控制器进行的仿真比对实验,验证了该方法在闭环姿态控制系统的容错控制领域的应用优势,较好地解决了低轨遥感卫星动量轮故障频发的问题。
