基于异步优势执行器评价器的自适应PID控制

， ，，

(中国石油大学(华东) 计算机与通信工程学院，山东 青岛 266580)

0 引言

PID控制具有鲁棒性高且易于操作等优点，是现代工业中广泛应用的一种控制方法[1]。然而，传统PID的参数一旦确定就无法在线调整，难以满足时变系统的控制要求。自适应PID在传统PID的基础上引入了在线调参的思想，使其能够根据系统状态的变化调整PID参数，提高了系统的响应速度。目前应用比较广泛的自适应PID控制器有：模糊自适应PID控制器[2]，它以误差和误差变化率作为输入，通过查询模糊矩阵表进行参数调整，从而满足PID参数自整定的要求，但这种设计方法需要较多的先验知识，存在大量的参数优化问题[3]；基于神经网络的自适应PID控制[4]，利用神经网络对于非线性结构的良好逼近能力，无需辨识复杂的非线性被控对象就能够达到有效的控制，但是获取监督学习中的教师信号仍然存在困难[5]；进化算法自适应PID控制器[6]，虽然对于先验知识要求较少，但是在实际工程中难以实现实时控制；强化学习自适应PID控制器[7]，利用强化学习非监督特性解决了教师信号难以获取的问题，这类控制器需要较少的先验知识而且控制过程无需复杂的参数优化。其中执行器-评价器(Actor-Critic，AC)自适应PID[8]是应用最为广泛的强化学习控制器，该控制器提出了一种结合AC结构实现在线调整参数并采用神经网络逼近马氏决策过程中的值函数和决策函数的设计思路，但由于AC算法中前后学习数据的相互关联性，影响了控制器的收敛速度[9]。

Google的DeepMind团队提出的异步优势执行器评价器(Asynchronous Advantage Actor-Critic，A3C)学习算法[10]利用CPU多线程并行的特性，在CPU多线程上异步地训练多个智能体(agent)，并行中的agent会经历不同的学习状态，从而打破了学习样本的相关性[11]，这种高效的异步结构执行方式已经应用到多个领域[12]。本文结合A3C结构多线程异步训练的方式以及强化学习的无模型在线学习能力，使用BP神经网络作为函数逼近器，最终研究提出了一种基于异步优势执行器评价器的自适应PID控制器设计方法，并在仿真实验中验证了该方法的优越性和有效性。

1 系统结构及原理

1.1 增量式PID控制原理

数字PID控制可分为两类，其中包括位置式PID与增量式PID[13]。增量式PID是一种通过对控制量的增量进行PID控制的算法，其计算公式见式(1)：

u(t)=u(t-1)+Δu(t)=u(t-1)+Ki(t)e(t)+

Kp(t)Δe(t)+Kd(t)Δ2e(t)

(1)

其中：

e(t)=y′(t)-y(t)，

Δe(t)=e(t)-e(t-1)，

Δ2e(t)=e(t)-2*e(t-1)+e(t-2)

y′(t)表示当前的实际信号值，y(t)表示当前系统的输出值，e(t)表示当前误差，Δe(t)为一次误差，Δ2e(t)为二次误差。kP为比例系数，决定了控制程度的强弱，比例系数越大，系统的响应速度就越快，但是容易使系统发生震荡和超调。kI为积分系数可以消除系统的静态误差。kD为微分系数有助于减少系统超调量，提高系统的控制精度。不同的PID参数造成了控制系统的差异，控制过程中，根据系统的动态特性从而调整PID参数，往往会得到满意的控制效果。

在控制结构上，增量式PID控制较位置式PID控制取消了PID控制中积分环节的累计求和，节省了大量的计算性能和储存空间，为A3C算法的学习速率和学习样本的存储提供了保障。此外，增量式PID的每一次的输出为控制量的增量，在系统发生故障时对系统的影响程度较小，使得环境奖励更加稳定，保证了算法学习的收敛速度。

1.2 A3C学习算法结构

A3C算法是一种深度强化学习算法，该算法在Actor-Critic框架基础上引入了异步训练的思想，在提升控制性能的同时大大加快了训练速度。A3C学习框架由一个中央网络(Global Net)和多个Actor-Critic结构以及仿真环境组成，如图1所示。

图1 A3C算法结构图

由图1可见，A3C算法创建了多个agent，每个agent即为一个AC结构，包括一个决策网络和评价网络，算法将agent放置在相同的环境实例中并行执行和学习，提高了每个agent的学习速率。此外，A3C采用了中央网络的学习机制，打破了agent学习样本的相关性，其主要作用为更新和存储AC结构中决策网络和评价网络的参数，不同agent将自身的学习数据传递给中央网络用以更新自身参数，从而提高了收敛速率。其中，决策网络即Actor网络，负责学习最优策略，使得agent可以针对不同环境状态选择最优的决策，而评价网络即Critic网络，负责拟合价值函数，增强了agent对于环境的奖励感知能力。决策网络和评价网络的组合使用保证了学习算法的有效性和鲁棒性。

2 A3C-PID控制器设计

2.1 A3C-PID控制器结构

基于A3C学习的自适应PID控制器的设计思路就是在增量式PID控制器的基础上结合了A3C异步学习结构，其结构设计如图2所示。

图2 A3C-PID控制结构图

rm(t)=α1r1(t)+α2r2(t)

(2)

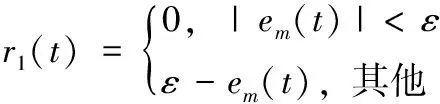
2.2 基于多层前馈神经网络的A3C-PID学习

多层前馈神经网络[14]又称BP神经网，是一种多层前向网络的反向传播算法，具有较强的非线性映射能力，适合于求解内部机制复杂的问题。因此，本文使用两个BP神经网络分别实现Actor策略函数和Critic值函数的学习，其网络结构如图3、图4所示。

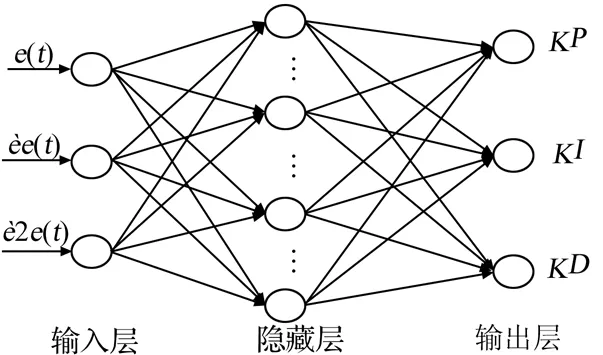
图3 Actor网络结构图

如图3所示，Actor网络共有3层：

第1层为输入层共有三个结点，输入向量S=[em(t),Δem(t),Δ2em(t)]T代表状态向量。

第2层为隐藏层设有20个结点，隐藏层与输入层之间没有设置激活函数，其隐藏层的输入为对输入层直接加权求和，如公式(3)：

(3)

其中：k表示隐藏层神经元的个数。隐藏层的输出使用了Relu6激活函数，其输出公式见式(4)：

hok(t)=min(max(hik(t),0),6)k=1,2,3…20

(4)

第3层为输出层设有三个结点，输出层的输入直接对隐藏层的输出进行加权求和，输出公式如式(5)所示：

(5)

输出层的输出使用softplus激活函数，其输出公式如式(6)：

yoo(t)=log(1+eyio(t))o=1,2,3

(6)

图4 Critic网络结构

δTD=qt-V(St,W’v)

(7)

qt=rt + 1+γrt + 2+ … +γn-1rt + n+γnV(St + n,W’v)

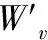
(8)

在计算出TD误差后，为打破学习样本的关联性，A3C结构中的每个Actor-Critic网络并不会直接更新自身的网络权值，而是用自身的梯度去更新中央网络存储的Actor-Critic网络参数，更新公式见公式(9)、公式(10)：

(9)

(10)

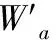
2.3 A3C-PID控制器网络初始化

网络的初始参数直接影响了闭环控制系统的稳定性，神经网络PID控制由于教师信号难以获取，需要按照经验或人工试凑确定网络参数。强化学习的非监督学习特性使得控制器通过K次迭代学习便可获取最优的网络初始参数。然而，AC-PID控制器由于AC算法获取的学习样本具有前后关联性，导致了较慢的收敛速度。相比之下，A3C-PID在CPU的多线程中异步学习网络参数，破坏了样本关联性，提高了收敛速率。A3C-PID网络参数学习过程与2.1节中叙述相似，但不同在于A3C-PID在迭代学习时设置m值为计算机CPU核心线程数，而当A3C-PID在线控制时m值设置为1。

2.4 A3C-PID控制器设计流程

基于A3C并行学习的体系结构和以n步TD误差为性能指标的网络学习方式，归纳出A3C-PID控制器的设计流程如下：

a)设置采样周期ts，A3C算法的线程个数m，更新周期n，通过K次迭代学习，初始化每个AC结构的网络参数；

b)计算系统误差em(t)，构造出系统状态向量Sm(t)，作为Actor(m)和Critic(m)的输入；

d)Actor(m)输出kP、kI、kD值，根据式(1)计算系统输出um(t)，并观测下一采样时间系统误差em(t+1)，根据式(2)计算奖励值函数rm(t)；

g)判断是否满足控制结束条件，若满足结束条件，退出控制，否则更新Sm(t)并返回步骤c)。

3 仿真实验

阶跃响应能够很大程度上反应系统的动态特性，是分析系统性能的重要手段。因此，为测试控制算法能够在系统特性动态改变的同时自适应地调整PID参数，进行了阶跃信号控制实验。被控制对象选为：

y(t)=1.2(1-0.8e-0.1·k)y(t-1)+u(t-1)

(11)

被控对象的初始状态取[0,0]，设采样时间为1 ms，A3C学习自适应PID控制的各个参数为：

m=4,αa=0.001,αc=0.01,ε=0.001

γ=0.9,n=30,K=3000

仿真结果见图5～8及表1。

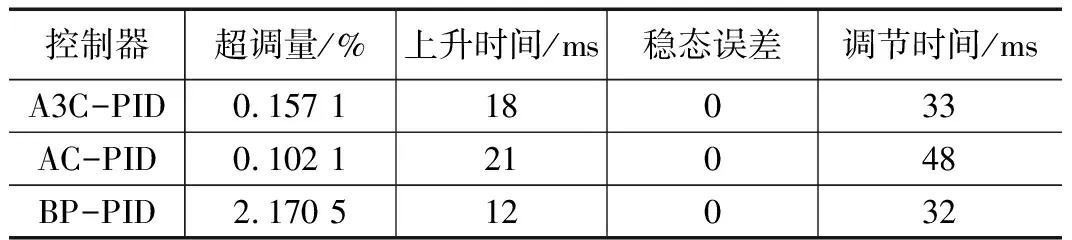
表1 控制器性能对比

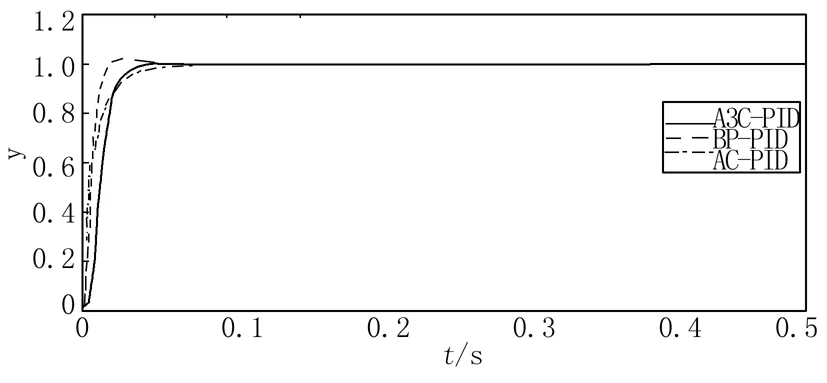
图5 位置跟踪

图5为A3C,BP,AC自适应PID控制器对于参考模型的位置跟踪结果；表1为A3C,BP,AC自适应PID控制器性能对比。从表1可以看出，三个控制器都有着较好的控制精度，即稳态误差都为0。在动态性能方面，见图5，在仿真初期(大约20个仿真周期内)，BP-PID控制器有着更快的响应速度，上升时间更短，为12 ms，但是BP-PID具有2.1705%的较高系统超调量。相反AC-PID和A3C-PID都具有较小的0.1571%和0.1021%的系统超调量，但是AC-PID的调节时间较长，为48 ms，上升时间21 ms。相比之下，A3C-PID控制器有着更好的控制稳定性和快速性。

图6 位置跟踪误差

图7 控制器参数整定结果

图6和图7分别为A3C-PID的跟踪误差以及PID控制器的参数自适应变换的过程。由图6～图7可以看出，A3C-PID控制器能够根据不同周期内的误差自适应调整PID参数值。在仿真开始阶段，由于系统跟踪误差较大，为保证系统有较快的响应速度，kP不断增大，kD逐渐减小，同时为避免系统出现较高的超调量，限制了kI的增加；随着误差不断减小，kP开始减小，为消除累计误差kI值逐渐增加，但同时造成了少量的超调，由于此阶段kD值于系统影响较大，所以趋于稳定；最终跟踪误差为0，kP、kI、kD值达到稳定状态。仿真结果可以看出，A3C-PID控制器有着良好的自适应能力。

强化学习的目标是学习最优策略从而最大化由起始状态到终止状态的折扣回报值U，计算公式见式(12)：

(12)

图8 强化学习折扣回报值曲线

图8为AC-PID与A3C-PID折扣回报值曲线。从图8可以看出，在进行3000次迭代训练后，A3C-PID相比AC-PID获得了更高的回报值。除此之外，A3C-PID在约1800次迭代训练后渐渐趋于稳定状态，而AC-PID在2500次迭代后才出现收敛的趋势。由此可得，A3C-PID相比AC-PID有着更快的收敛速度。

4 结束语

本文详细分析了多种自适应PID控制器，并在增量式PID控制器的基础上引入了A3C的异步学习体系。结合该体系，把多个AC结构置于相同环境中并行进行学习，为使控制器搜索到最优整定策略，使用BP神经网逼近每个AC

结构中的策略函数和值函数，并采用n步TD学习策略和Global Net机制异步更新Actor-Critic参数。最后通过仿真实验验证了A3C-PID有着较好的收敛速度和自适应能力，具有良好的系统跟踪性能。由此可见，本文提出了一种有效的自适应PID控制器，为实际控制应用奠定理论基础。