金属磁记忆信号屈服点特征

(中国石油西部管道公司,乌鲁木齐 830013)

20世纪90年代，俄罗斯科学家DOUBOV提出了金属磁记忆检测技术[1-2]，近年来，该技术在输油输气管道以及航天等领域有了极其普遍的应用[3-5]。金属磁记忆检测技术的检测机理是：金属构件受到载荷作用后，其应力集中区域的晶体内部会有一个不可逆的磁畴组织定向移动，相当于产生了一个磁极并在金属表面形成了漏磁场；应力消失后，磁场状态会被保留，可以认为是漏磁场“记忆”了金属构件的应力集中区[6-10]。其是一项不需要耦合剂，对被测试件无损坏，设备轻便的无损检测技术，近年来应用越来越广泛，而这项技术还有许多专业问题没有得到明确的解释，许多研究方向还有待开发，未来的发展潜力不容小觑。在实际检测中, 按照DOUBOV提出的磁记忆判定准则，有时并不能准确判断出缺陷的位置，因此，磁记忆信号测量的准确性也受到怀疑[11]。研究表明，在弹性范围内的应力集中的磁记忆信号特征已较为明确，而达到塑性变形时的磁记忆信号特征还没有确切解释，无法对铁磁金属的使用情况进行准确预测[12]。

笔者基于密度泛函理论建立了磁力学耦合模型，计算了应力作用下Fe晶体的晶格结构、差分电荷密度等的变化情况，从而分析了铁磁性材料屈服前后的磁记忆信号特征，为进一步研究金属磁记忆检测提供了理论依据。

1 磁力学模型建立理论

量子力学理论指出，轨道由内向外由电子一层层填满，物质磁性主要由外层电子提供，原子磁矩就是外层电子的总自旋磁矩[13-15]。根据量子理论，材料的晶体结构、自旋密度分布、能量变化会影响到物质的磁性，因此可通过计算系统的能量泛函E[ρ]和电子态密度ρ(r)来研究铁磁性材料的磁力学性质[16-18]。基于密度泛函理论的第一性原理表明，密度泛函理论实质上就是将多电子问题转变为单电子方程，这样物质的性质就可以用一个极其简单的单电子方程描述，而无需多余的条件。物质的基本物理性质可由电子态密度ρ(r)来表示。第一定理为：对于相互作用的多粒子系统，系统基态能量的基本变量由电子态密度ρ(r)表示。

将ρ(r)定义为

ρ(r)=〈Φ|Ψ+(r)Ψ(r)Φ〉

(1)

式中:Φ为基态波函数；Ψ+(r)为在r处产生一个粒子的费密子场算符；Ψ(r)为在r处消失一个粒子的费密子场算符。

第二定理为：当总粒子数不变时,将能量泛函E[ρ]对电子态密度ρ(r)取极小值，即为系统的基态能量。

对于给定的υ(r)，能量泛函E[ρ]为

(2)

式中:T为电子动能，MeV;U为库仑排斥项;V为局域势υ(r)对外场的影响。

将式(2)对密度函数ρ(r)变分，得到系统的基态能量为

(3)

即可得到：

(4)

式中：εi为拉格朗日乘子；Veff为有效势，由外势、库仑势及交换关联势组成。

式(4)为单电子方程，可求解多粒子体系磁力学关系，其中有效势Veff[ρ(r)]为

(5)

式中：Exc[ρ(r)]为交换-关联泛函。

在量子力学中，自旋的工作方式与经典力学的角动量相似。它是粒子的内在特征，并会由此产生磁场。自旋与自转实际上是两种完全不同的性质，自转其实是物体相对于质心的旋转。材料受到载荷作用时，可通过求解电子密度分布函数ρ(r)来研究多粒子体系的磁力学特性[19-21]。

2 铁磁金属的第一性原理仿真分析

2.1 模型建立

文章主要讨论铁磁金属在应力到达临界屈服点前后时的晶体性质以及磁记忆信号特征[22]，由于铁磁金属主要含有Fe元素，因此，利用CASTEP软件，建立Fe晶体模型，分别建立了α-Fe的单原胞结构和2×2×2超原胞结构模型，如图1所示。

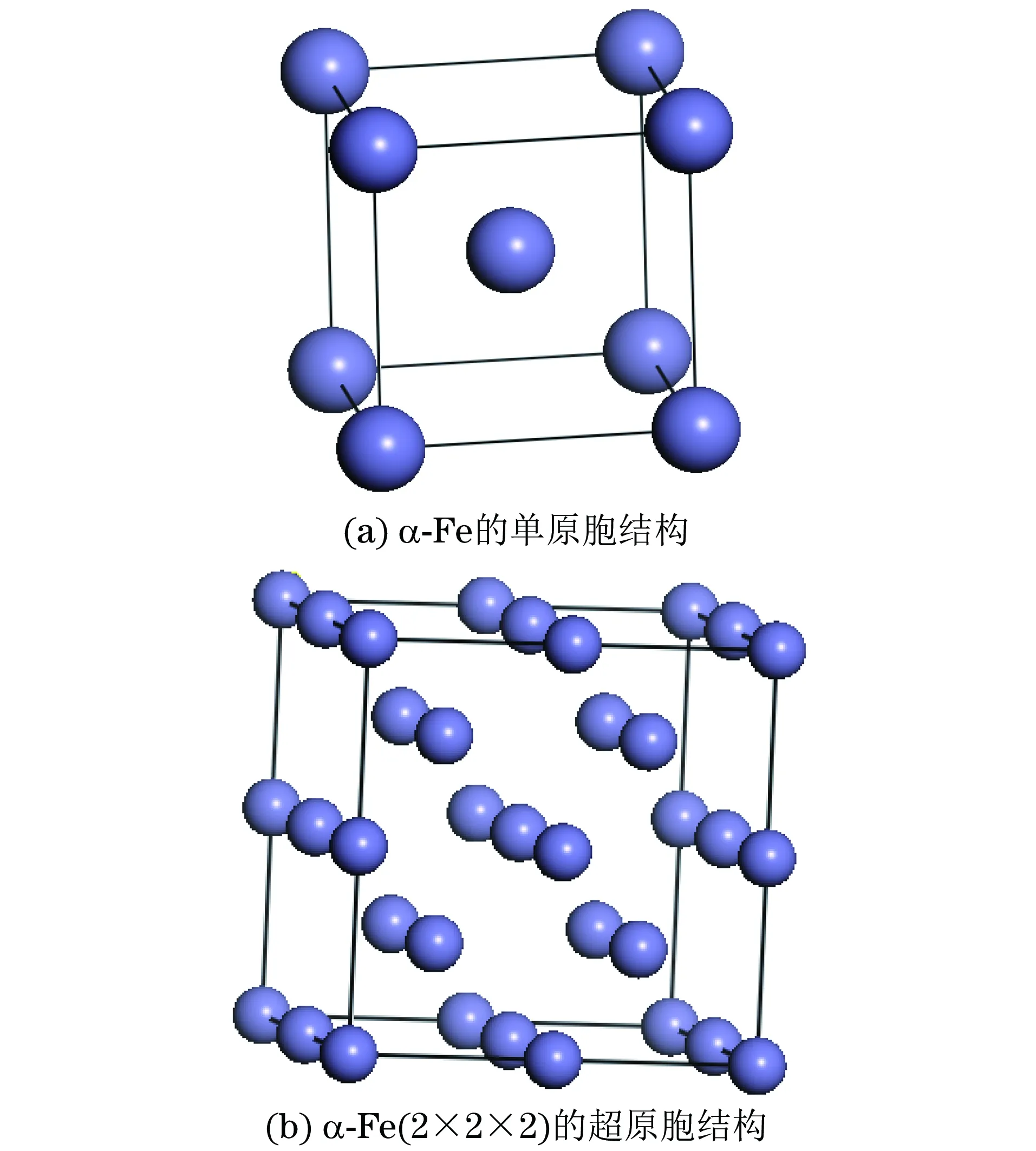
图1 Fe的力磁耦合模型

对Fe的体心立方(bcc)和六角密堆积(hcp)结构在平衡状态下采用不同算法进行计算，结果如表1所示。

由表1对比发现，PBE和RPBE两种交换关联能算法所计算的晶格常数与c/a(晶格常数比)值和试验值的差异有些悬殊，作为计算使用，误差比较大，因此不宜选用PBE和RPBE这两种交换关联能算法。而PW91算法计算出的晶格常数和c/a值与试验值非常接近，作为计算使用误差比较小，由此可知，计算Fe晶体的磁力学关系最适合的函数应为PW91。

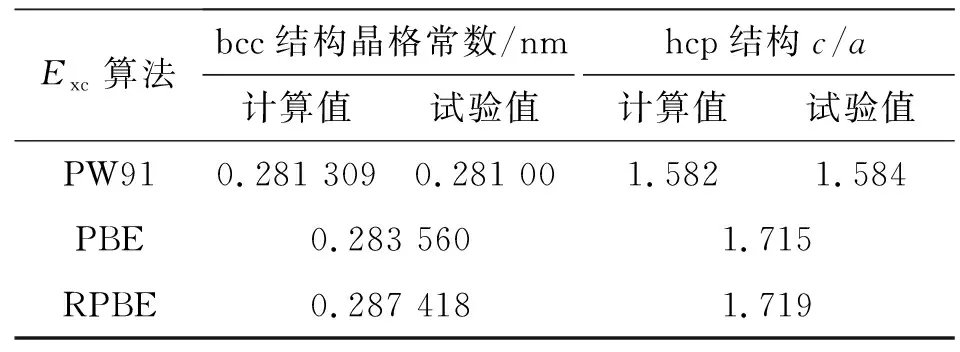
表1 Fe的两种结构的平衡状态下交换关联

2.2 差分电荷密度的计算

外部载荷作用于材料时，材料受到应力作用，其内部原子也会受到应力作用，从而产生一系列的微观变化。晶体内部原子之间的相互作用将被改变，进而使得自旋极化差分电荷密度分布受到影响，从而改变固体的磁特性。图2为不同压力下Fe的差分电荷密度分布。

图2 Fe在不同压力作用下的差分电荷密度分布

由图2可以看出，应力增加时，处于中心的原子作用面积减小，并且四周不同原子层上的电子密度分布面积有所变化，这表明原子彼此的作用力随着应力的增大而逐步减弱，晶体内部原子之间的成键能力减弱，进而降低了晶体结构的稳定性。并且，当应力集中到达一定水平时，晶体结构发生改变，即由bcc结构转变为hcp结构。

2.3 临界屈服点的计算

物质在不同阶段之间的相互转变叫相变。广义上来说，物质的相由特定分界面与其他部分分离开，物质不同的相具有相同的物理性质。金属在特定条件下会发生相变，一般来说,相变总是发生在一定的压力和温度下。当应力超过Fe晶体晶格的屈服点时,随着应力的增加,原子形态逐渐沿变形方向延伸,逐步导致晶格的完全畸变,Fe从bcc结构转变为hcp结构，形成新相，而晶体处于塑性变形状态。

笔者利用焓相等的条件，计算了Fe从bcc结构转变为hcp结构的临界屈服压力，约为10.5 GPa，与其他文献研究一致。两种Fe相的压力与能量关系曲线(见图3)约在10.5 GPa处相交。

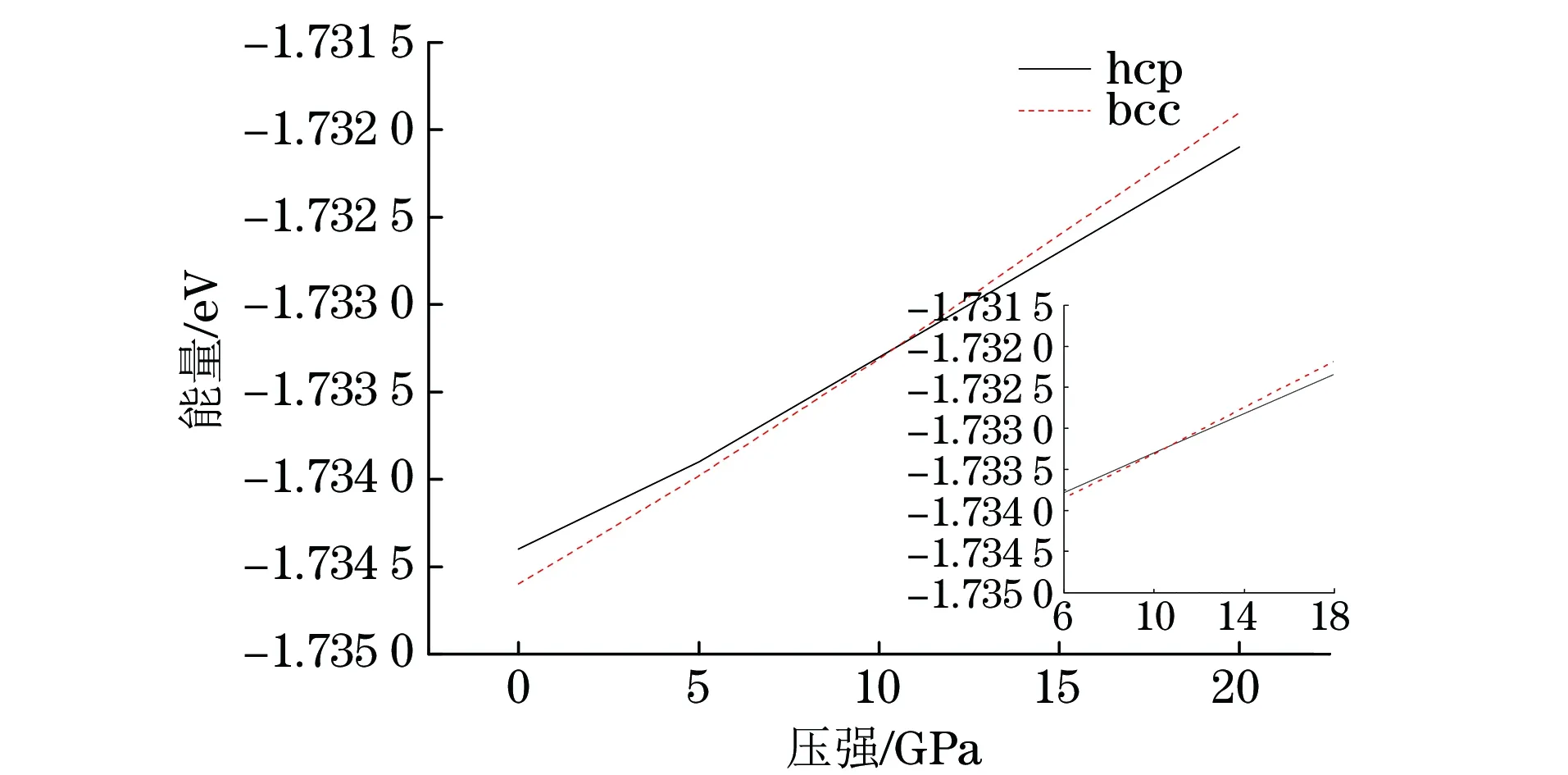
图3 两种Fe相的能量与压力的关系曲线

根据Stoner定律[22]，原子磁矩与材料的磁记忆信号(以B表征)具有如下关系

(6)

式中：B0为外界磁场的磁感应强度；Bi为材料本身的磁感应强度；M为磁化强度；H为外界磁场强度；μ0为真空磁导率；μi为原子磁矩。

由式(6)可知，在地磁场环境下，随着应力的变化，磁记忆信号也将发生一定变化。当应力集中达到临界屈服点时，铁磁性材料内部晶体结构将发生相变，原子磁矩发生突变，磁记忆信号也将发生突变。

材料内部广泛存在一种缺陷，即位错。位错的存在对材料的机械性能有着十分显著的影响。由于理想晶体不存在实际晶体内部存在的位错等缺陷，因此理论上的滑移切应力要比实际晶体的滑移切应力大得多，理想晶体的屈服应力比实际晶体的屈服应力大。所以，仿真时需要引入校正因子，但实际晶体的屈服应力与理想晶体的屈服应力的对应关系还需进一步研究。

3 试验与结果分析

文章进行了钢管打压试验，研究铁磁金属弹性形变到塑性形变过渡点前后的磁记忆信号变化特征。试验前，先将高压盲板焊接在钢管的两边，并将水喷嘴焊接在每个封口处，在钢管两边封品处分别接一个注水口和一个压力传感器；然后，对测试钢管进行网格划分, 并在所有网格点上安装磁记忆传感器探头。通过磁记忆检测系统，在钢管打压前后采集了磁记忆信号。磁记忆传感器探头的分布示意如图4所示。

对具有应力集中的管道进行5次循环加压，每次都从0 MPa开始打压，分别打压到6，10，12.5，12.5，12.5 MPa，所采集的磁记忆信号为铁磁材料表面磁场信号的切向分量。图5为5次循环打压后的磁记忆信号随应力的变化曲线。

由图5(a)，5(b)可见，在钢管的第一次和第二次打压过程中，磁记忆信号随着压力的增加呈线性增加，信号曲线斜率变化不大，表明材料的晶体结构没有变化，物理性质没有受到影响。由图5(c)可见，在压力达到12 MPa之前,信号先随着压力的增加而增加，随后约在12 MPa左右，信号曲线出现拐点，曲线斜率突然增大。如图5(d)，5(e)所示，压力越大，信号呈线性增加，但与第三次打压相比，信号的曲线斜率明显减小，表明在第三次打压后，材料的晶体结构发生了变化，该物质的磁性受到了很大影响。

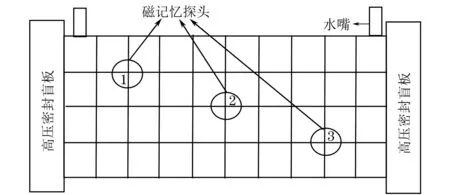
图4 磁记忆探头分布示意

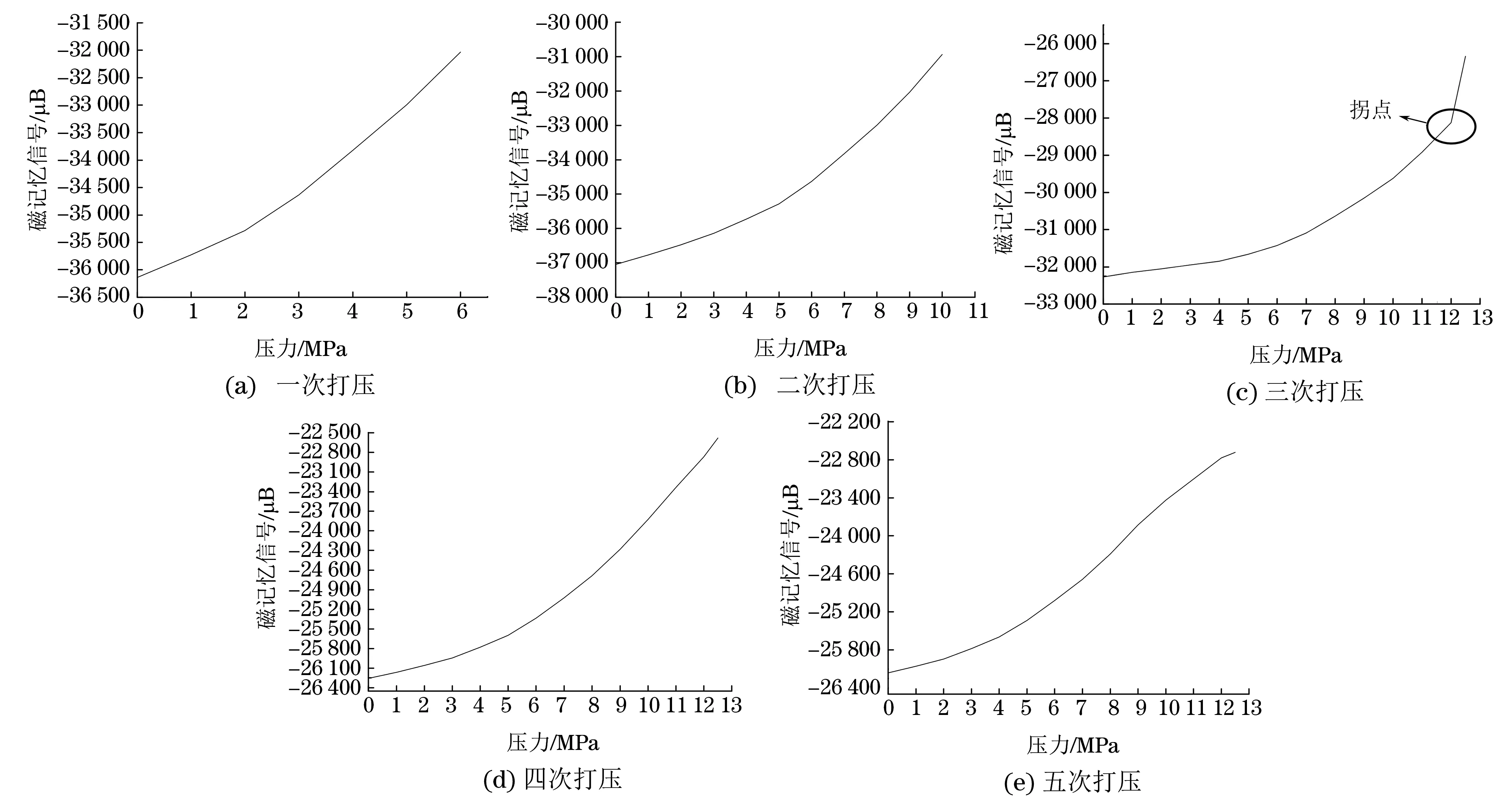
图5 5次循环打压过程中磁记忆信号与应力的关系曲线

4 结论

基于密度泛函理论建立了磁力学耦合模型，详细讨论了钢管屈服前后的磁记忆信号特征及相变后Fe的磁特性变化情况。结果表明：随着应力增加，晶体内部原子之间的成键能力减弱，晶体结构的稳定性降低，当应力集中达到一定水平时，铁磁金属Fe由bcc结构转变为hcp结构；当应力集中程度达到铁磁性金属构件的临界屈服点时，金属的磁力学特性开始减弱。通过计算可得，Fe从bcc结构到hcp结构发生相变的临界压力约为10.5 GPa，试验结果中，铁磁性金属构件的临界屈服应力约为12 MPa，二者具有一定的对应关系，需引入一个修正因子，其具体对应关系还需进一步研究。