小径钛钢爆炸复合棒材超声检测信号时频分析

, ,

(南昌航空大学 测试与光电工程学院,南昌 330063)

爆炸复合材料是两种不同的金属材料在炸药的能量(爆轰波)作用下，实现高速碰撞形成的新的复合材料，常见材料有钛/钢、不锈钢/钢、锆/钢、铜/钢等，从外形上来分又有板材和棒材两种[1]。爆炸复合材料在高温高压及要求较高的抗腐蚀等场合，有着广泛的应用。

爆炸复合的本质是在外力的作用下将两种金属接合在一起，金属的接合面形态表现出波纹状。一般来说波纹波幅越大，结合强度越好。行业标准NB/T 47002.1-47002.4-2009《压力容器用爆炸焊接复合板》中，除要求对复合材料的剪切、拉伸、冲击、弯曲等力学性能进行检验外，还特别规定需采用超声无损检测方法来评价复合面接合品质。

超声检测信号是一种非平稳时变信号，超声始波从发出经被检工件到回波信号被接收，有着非常显著的幅值、频率随时间变化的特点。时频分析作为分析时变非平稳信号的有力工具，提供了时间域与频率域的联合分布信息，清楚地描述了信号频率随时间变化的关系。利用时频分析方法来分析信号，能得到各时刻的信号瞬时频率及其幅值，该方法也成为现代信号处理研究的热点[2]。将该方法应用于爆炸焊接复合材料、超声检测的信号处理中，可以得到复合面的形态特征，为爆炸复合工艺水平的评价提供参考。

1 短时傅里叶时频分析[3]

利用时间和频率的联合函数来表示信号特征简称为信号的时频分析，时频分析是处理非平稳时变信号的强有力工具。其中,傅里叶变换建立了信号从时域到频域的变换桥梁，但它的不足是在整体上将信号分解为不同的频率信息，不能揭示某种频率分量出现在什么时候及其随时间变化的情况。为达到时域上的局部化，Gabor提出了短时傅里叶分析方法。该方法的基本思想是在信号傅里叶变换前乘上一个时间有限的窗函数，并假定非平稳信号在分析窗的短时间内是平稳的，通过窗在时间轴上的移动而使信号逐段进入分析状态，从而得到信号的时变特性。其定义如下所述。

给定一个时间宽度很短的窗函数η(t)，让窗滑动，则信号z(t)的短时傅里叶变换(STFT)定义为

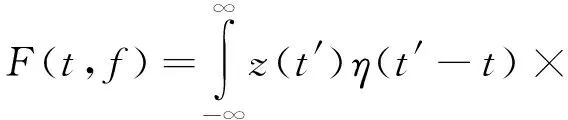
exp(-j2πft′)dt′

(1)

式中：t为时间；f为频率。

由式(1)可见，正是窗函数η(t)的存在，使得短时傅里叶变换具有了局域特性，其既是时间的函数，也是频率的函数。对于给定的时间t，F(t,f)可看作是该时刻的频谱。特别地，当窗函数取η(t)=1,∀t时，短时傅里叶变换就退化为传统的傅里叶变换。

式(1)表明，信号z(t′)在时间t处的短时傅里叶变换就是信号乘上一个以t为中心的“分析窗”η(t′-t)后所作的傅里叶变换。因为信号z(t′)乘以一个短窗函数η(t′-t)等价于取出信号在分析时间点t附近的一个切片，所以短时傅里叶变换F(t,f)可以理解为信号z(t′)在时间点t附近的傅里叶变换，即“局部频谱”。

窗函数η(t)的中心E{η(t)}和半径Δ(η)分别定义为

(2)

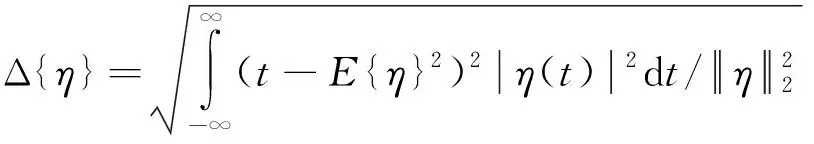
(3)

窗函数η(t)的宽度为2Δ(η)。根据定义，短时傅里叶变换得到时窗[E{η)+t-Δ{η},E{η}+t+Δ{η}]和频窗[E{Γ}+f-Δ{Γ},E{Γ}+f+Δ{Γ}]中信号的局部信息。选定窗函数η(t)之后，这个时频窗是一个与两坐标轴平行、与时间t和频率f无关的矩形，具有固定的面积4Δ{η}Δ{Γ}。短时傅里叶变换的时频分析能力可以用时频窗矩形的形状和面积来度量：在时频窗的形状固定不变时，窗口面积越小，说明时频局部化描述能力就强；窗口面积越大，说明时频局部化描述能力越差。单一的时间-频率变化称为线性时频，即将信号分解为基本的分量;而将信号在时频面上的能量分布，称为二次变换，常用谱图来表示。二次变换定义为短时傅里叶变换模的平方，即

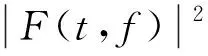
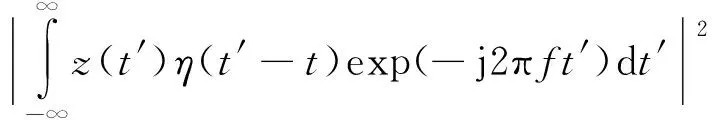
(4)

从式(4)可看出，其是实值、非负的二次型分布。

2 小径棒材超声检测

某一小径爆炸复合棒材工件实物及水浸超声检测的扫查方式如图1所示，图中D1为钛直径,D2为棒材的外径。

图1 爆炸复合棒材工件实物及水浸超声检测扫查方式

棒材芯部为钛,外部为钢，钛直径D1为24 mm，整个外径D2为28 mm。为了保证耦合良好，采用水浸超声检测方法，探头频率为15 MHz，检测仪器为OLYMPUS 5077 PR，数据采集器型号为PicoScope 3206D，采集频率为500 MHz，沿工件轴向步进0.5 mm扫查采集A扫信号。

2.1 信号特点

超声在钢和钛中的传播速度分别为5 900,6 100 m·s-1，采样频率为500 MHz，在时域分辨率上为2 ns，约合12 μm。采集到的某帧信号如图2所示。

从图2可以看出，小径爆炸复合棒材水浸超声信号较为复杂，其中有效信号(①～⑥)经过水层、外部钢层，芯部钛层等多次反射，从时域上看接收信号幅值有较大的误差。为了分辨出复合面形貌，从时域上读出③～④或⑤～⑥之间的值，通常取时域上的最大值经声速换算成长度值，如图3所示。

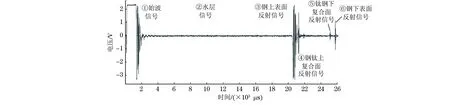
图2 小径爆炸复合棒材水浸超声信号

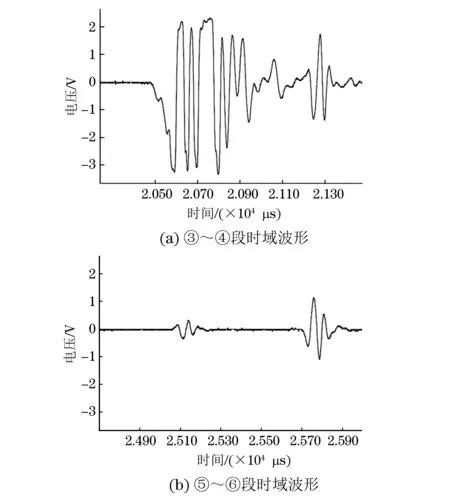
图3 复合层时域信号

将复合层信号放大后发现，由于受信号干扰及衰减等因素影响，时域上会出现多个最大值，无法准确读取时间点。

2.2 检测信号分析

短时傅里叶变换可以将时间-幅值转换成时间-能量的二次时频分析，将接收信号能量的最大值作为信号时间点，可以有效克服时域信号无法解决的问题。对整个信号进行短时傅里叶变换，结果如图4所示。

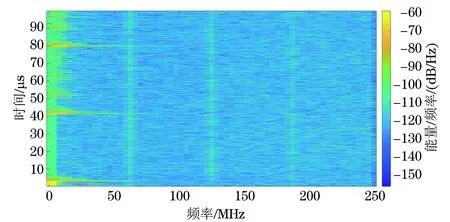
图4 全部信号的短时傅里叶变换

选用Hanning窗，窗函数的长度为128，从图4可以看出，在始波及复合层处能量有集中，频率集中在7.812 5 MHz～15.625 MHz之间。分别取两个复合层之间的信号做短时傅里叶变换，如图5,6所示。

从图5，6中经短时傅里叶时频二次分析，可以得出时间-能量关系曲线具有以下特征：

(1) 将接收信号能量最大值作为时间分析点，随着接收信号时间的不同，信号能量逐渐减小，符合超声检测的基本原理；

(2) 相比时间-幅度信号，二次时频信号曲线光滑且具有极大值点，便于读取时间点信号；

(3) 能量最大值发生在时域上第一个最大值附近，与时域判别一致且有较高的准确性。

列出在2种不同频率处能量的最大值时间点，如表1所示。

2.3 测试结果

在中心频率为11.7 MHz和15.625 MHz处读取能量最大值,换算成差值后误差很小，都能够作为读取时间点。这是因为探头中心频率为15 MHz，实际会有一定的偏差；而且超声信号经钢和钛两种不同声阻抗材料散射后会有相应的频率偏移。取中心频率为11.7 MHz处计算：500 MHz采样率时间分辨率为2 μs/格，声速为6 000 m·s-1(6 μm·ns-1)，从图5中读出上表面钢层厚度为3.672 mm，下表面钢层厚度为3.864 mm，与实际测试值误差在200 μm范围以内。

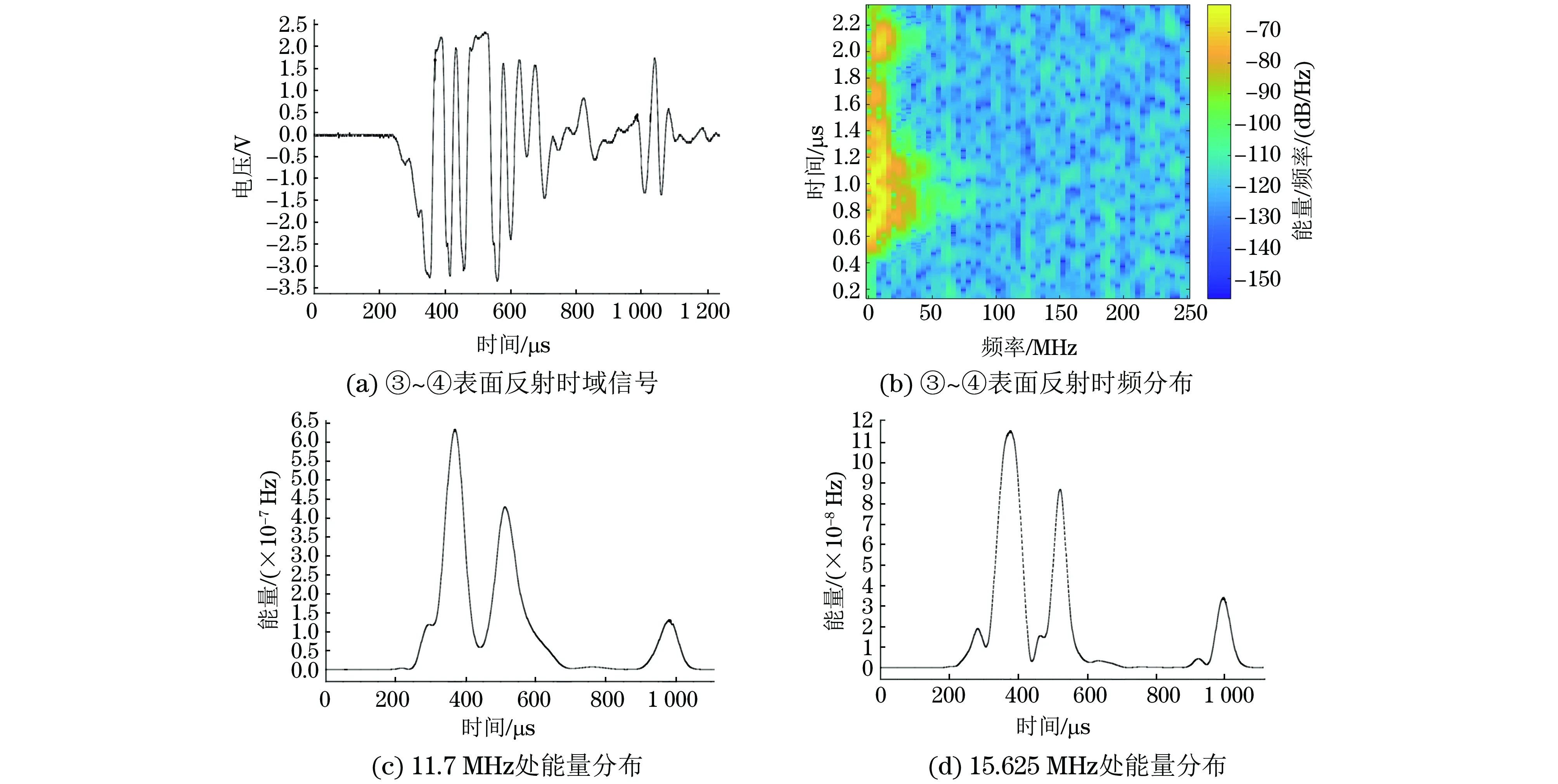
图5 ③～④复合面信号的短时傅里叶变换

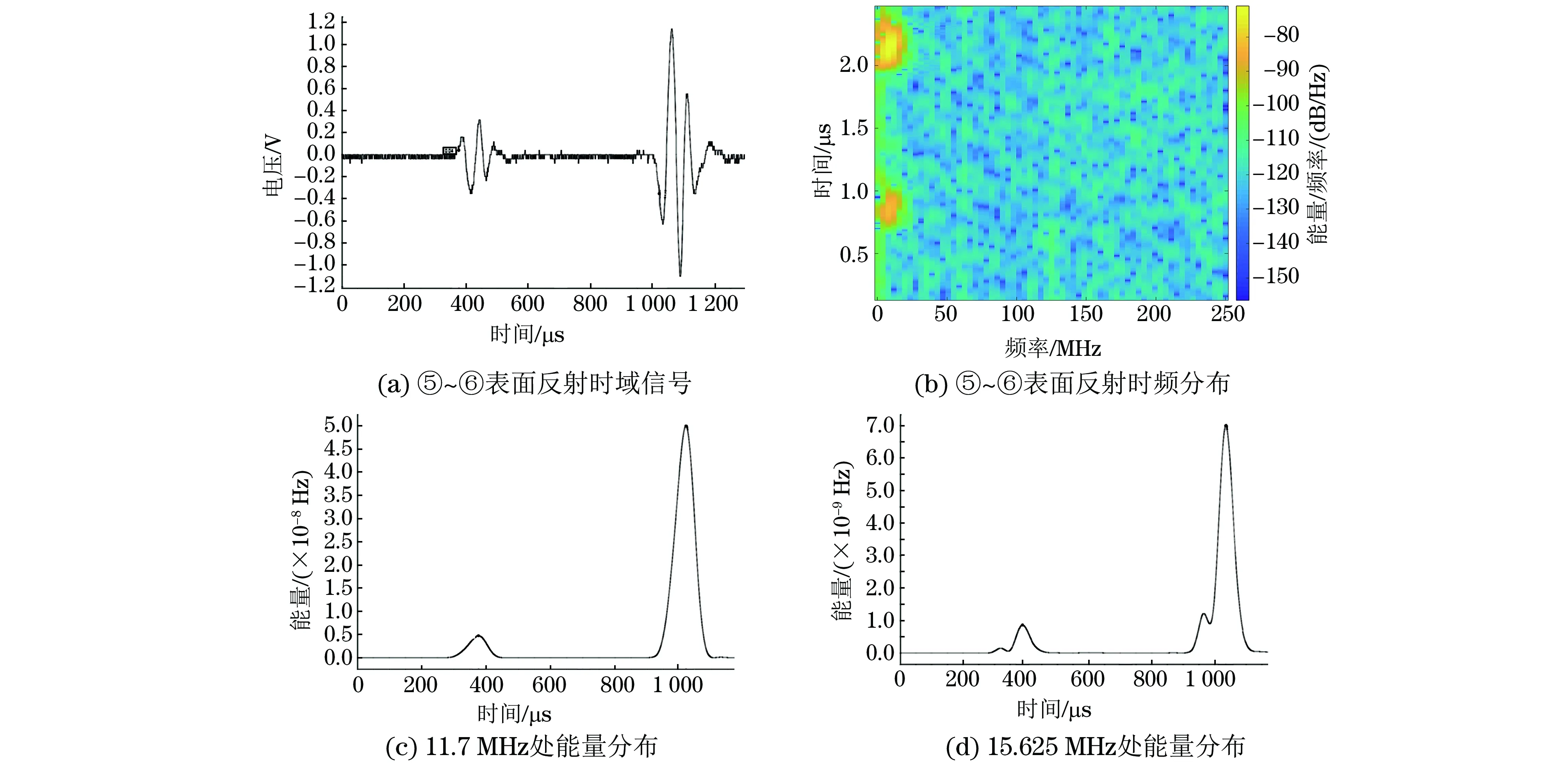
图6 ⑤～⑥复合面信号的短时傅里叶变换

μs

3 结论

将短时傅里叶变换时频分析方法用于小径管爆炸复合棒材复合面的检测中，可以有效分辨出时间-能量分布点，为检测复合面形态提供了一种方法。

由于接收的超声非稳态信号在时间上还有频率变化，其他时频分析方法，如分数阶短时傅里叶变换、连续小波变换、小波模极大值和Hilbert变换瞬时频率等，都可以从时间上分辨出频率畸变点，以畸变点作为信号点判别依据，有待进一步研究。