基于自适应随机优化的连续阵风关键载荷预测
2019-03-04肖宇
肖宇
中国商飞上海飞机设计研究院 结构强度研究所,上海 201210
对于民用客机来说,连续阵风载荷是设计载荷的关键组成部分,对民机设计与取证都具有极其重要的意义[1]。适航条款针对阵风载荷,提出在设计范围内,须满足相应的强度要求,以确保整个设计包线内飞机结构的完整性。为此,设计人员需要在包线边界上以及内部选择足够多的载荷工况进行评估,确认飞机结构所有部件对应的关键受载工况都可被准确识别,用于下游专业进行强度校核。
因此,一方面,对于一轮载荷分析,理论上需要计算的工况会达到100万的量级,其中对于常规构型的民用飞机,设计员可以通过现有经验筛选,进而缩减至10万的量级[2]。然而,对于目前的载荷分析模型,其结构上相临2站位的关键工况极有可能一致,实际上供下游专业强度校核的严重工况较少,因此大量的工况无计算的意义。
另一方面,对于非常规布局的民用飞机[3],如采用大展弦比机翼等设计[4],可能涉及到各种非线性效应[5],导致其飞行包线以及关键载荷工况将会与现有型号截然不同,因此将无法从现有经验来实现载荷工况的缩减,进而导致设计周期及费用的大幅增加,而考虑到其中大量载荷工况的不必要性,有必要开展关键载荷的主动识别技术研究,通过对这些关键工况的搜寻,避免大部分不构成包线工况的计算,从而显著提高阵风载荷计算的效率。
近些年,国外在此领域进行了较多的研究[6],如欧盟在FFAST(Future Fast Aeroelastic Simulation Technologies)项目中第1项专题便是关键载荷的识别,在该项目资助下,Khodaparast等[2]采用Kriging建立代理模型,并基于基因优化算法实现了对1-cos型离散阵风的关键载荷识别,随后Khodaparast和Cooper[7]又应用于模型更改后的快速载荷计算中。Cavagna等[8]则采用神经网络构建了代理模型,并与阵风气弹求解器耦合,开发了软件Fast-GLP(Fast tool for worst case Gust Load Prediction),通过数值模拟,表明了关键载荷预测的准确性。Castellani等[9]则采用参数化模型降阶的方法进行了动载荷的快速预测,效率同样获得了较为显著的提升。
但上述研究中大都针对连续的变量进行识别,同时商载、油载等重量分布情况也未予以考虑,而国内民机阵风载荷计算中[10],在各特征重量、各飞行高度下,必须真实考虑燃油消耗逻辑次序进行重量分布计算,因此在工程中只能事先对关键特征参数进行离散,从而形成大量的工况文件。对于这些真实考虑燃油消耗逻辑的阵风载荷工况,对其进行关键载荷的准确识别,具有较大的挑战。
鉴于此,本文针对国内民机型号工作,创新性地提出了一种采用自适应随机优化算法的阵风关键工况分析流程。首先,通过DoE(Design of Experiment)[11]方法,计算初始工况并建立初始代理模型,同时采用自适应随机优化算法,在极值载荷工况附近寻找新的可能极值工况,进行计算并更新代理模型,在迭代收敛后即可确定所关注载荷的全局最大值。然后,以某型民机侧向连续阵风模型作为算例,结果显示,在现有阵风模型计算过程中,本文方法由于避免大量不必要工况的计算,可以有效地提高连续阵风关键载荷的预测效率。
1 计算方法
1.1 初始值设定
采用DoE方法生成计算模型的初始样本点,以尽量少的计算次数,获取到尽量多的模型特性。DoE方法可以分为3类:一是因子类设计(factorial designs),二是响应面类设计(response-surface designs),三是随机类设计(randomized designs)。图1依次给出了三维空间内,3种模型产生的样本点对比,其中黑色点即为样本点。从图1可以看出,二水平全因子(2LFF)采样与Box-Behnken采样的样本点都在边界上,而拉丁超立方采样(Latin hypercube sampling)则大部分样本点存在于内部、且具有随机性,考虑到目前工程中阵风载荷计算工况出现在边界的概率较大,本文基于前2种方法开展对比分析研究。

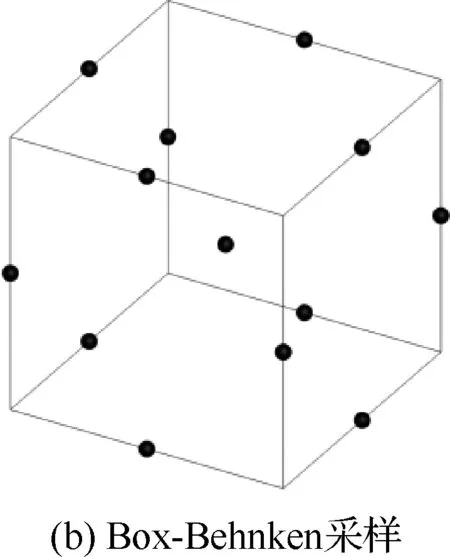
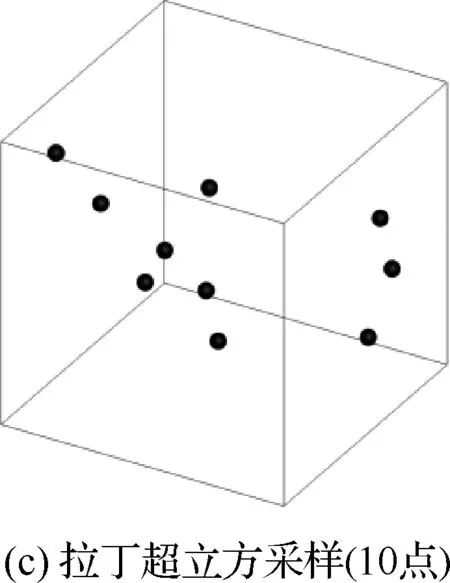
图1 3种典型DoE方法对比Fig.1 Comparison of three typical DoE approaches
1.2 代理模型构建
考虑到单个工况计算耗时较多,有必要建立一个可以快速评估的代理模型来替代原有的阵风计算模型,进而降低计算量,便于后续优化工作的开展。代理模型典型的有多项式响应面[12]、Kriging[13]、径向基函数[14]、人工神经网络[15]、支持向量机[16]等,综合考虑计算效率、精度以及模型透明性,本文采用多元自适应回归样条(MARS)模型[17]进行构建,该方法相对Kriging法,其计算效率较高,同时无需像径向基函数法一样事先假设复杂非线性基函数形状,因此具有一定的优势。
MARS方法由Friedman[17]首次提出,其采用简单的铰链函数(hinge function)及其积作为基函数,基函数形式及个数可以按精度要求自动确定,因此具有较强的自适应性,研究表明,该方法在样本数50~1 000,以及变量维数3~20具有较明显的优势[17]。
MARS所采用的铰链函数为
(1)
(2)
式中:下标+表示函数取正部分;t为节点坐标值。两者可构成一个映射对,所有的映射对可构成集合C,即
C={(xj-t)+,(t-xj)+}
t∈{x1j,x2j,…,xNj},j∈{1,2,…,p}
(3)
式中:N为样本空间维数;p为样本点个数。MARS构建过程中采用的基函数皆来自于集合C中的任意一个或多个铰链函数的乘积。
整个建模分为前向和后向2个过程,最终的代理模型为
(4)
式中:hm为基函数;βm为各基函数的权重;M为基函数总数。具体过程参见文献[17]。
1.3 基于自适应随机算法的优化模型
本文采用自适应随机优化算法开展关键工况的挑选[18]。假设可能的未知关键工况位于当前关键工况的附近,且满足截断正态分布规律,图2给出了参数x在标准差σ为0.2、0.5、0.7下的概率密度曲线对比,其中x取值范围为[1,7],最优点(即当前关键工况)为4。从图2可以看出,概率密度在最优点达到最大值,随着与最优点的距离增大概率逐渐趋近于0,同时在取值范围外概率则严格等于0,确保只在参数的有效范围内取值。另外,随着标准差σ减小,搜索范围逐渐减小。
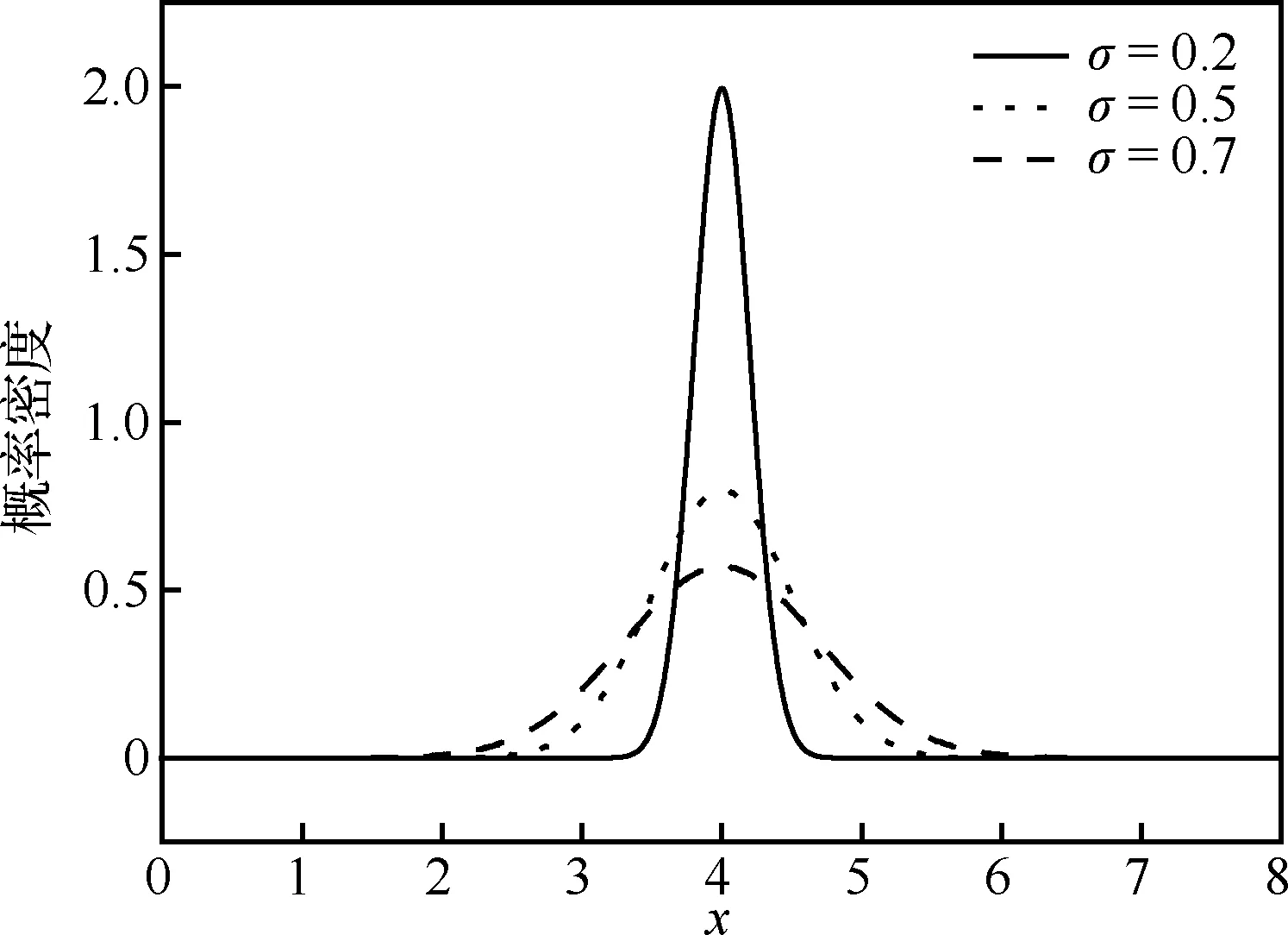
图2 截断正态分布概率密度曲线Fig.2 Function of probability density for truncated normal distribution
获取得到当前最优工况后,在其附近随机生成的若干个样本点,计算样本点与最优点的距离值,同时采用所建立的代理模型,评估得到所有工况的目标值,在此基础上,将归一化的目标值与距离值以一定的权重系数求和,从而得到下一次计算的工况。
考虑到本文所有计算针对的是离散的工况文件,上述样本点计算时都需采取一定的策略映射到真实的工况集,本文假定样本点定义域为整数域,从而可快捷地实现映射的目的。
另外,为提高鲁棒性及收敛性,在随机数生成的过程中,采用自适应技术确定标准差σ,给定σmax和σmin,初始标准差设定为σmax,在进行nf次连续的失败关键工况识别后将减小标准差,而在进行ns次连续的成功关键工况识别后增大标准差以提高收敛速度,最终在标准差值达到σmin后认为计算得到收敛,从而达到实现自适应调节计算参数的目的。
1.4 阵风关键载荷计算
本文阵风关键载荷的计算流程如图3所示。首先,依所选用的DoE方法确定初始工况,并通过建立的阵风气弹模型计算得到各载荷值;然后,在此基础上通过MARS方法建立初始代理模型,在极值载荷工况附近通过随机优化方法得到下一个可能的极值工况,通过记录比较连续失败次数nf和连续成功次数ns,实现自适应的调整标准差,重复进行迭代,直到计算流程收敛。
2 模型验证
2.1 模型介绍
针对某高平尾、下单翼、尾吊型飞机的侧向连续阵风关键载荷开展建模研究,其外形如图4所示,主要计算参数如表1所示。
采用梁架单元、偶极子网格法建立阵风载荷气弹耦合分析模型,如图5所示。系统、燃油、商载、发动机等质量以等效方式挂载至相应节点,另外,在机翼和平尾上布置若干单元用于气动与结构的插值。
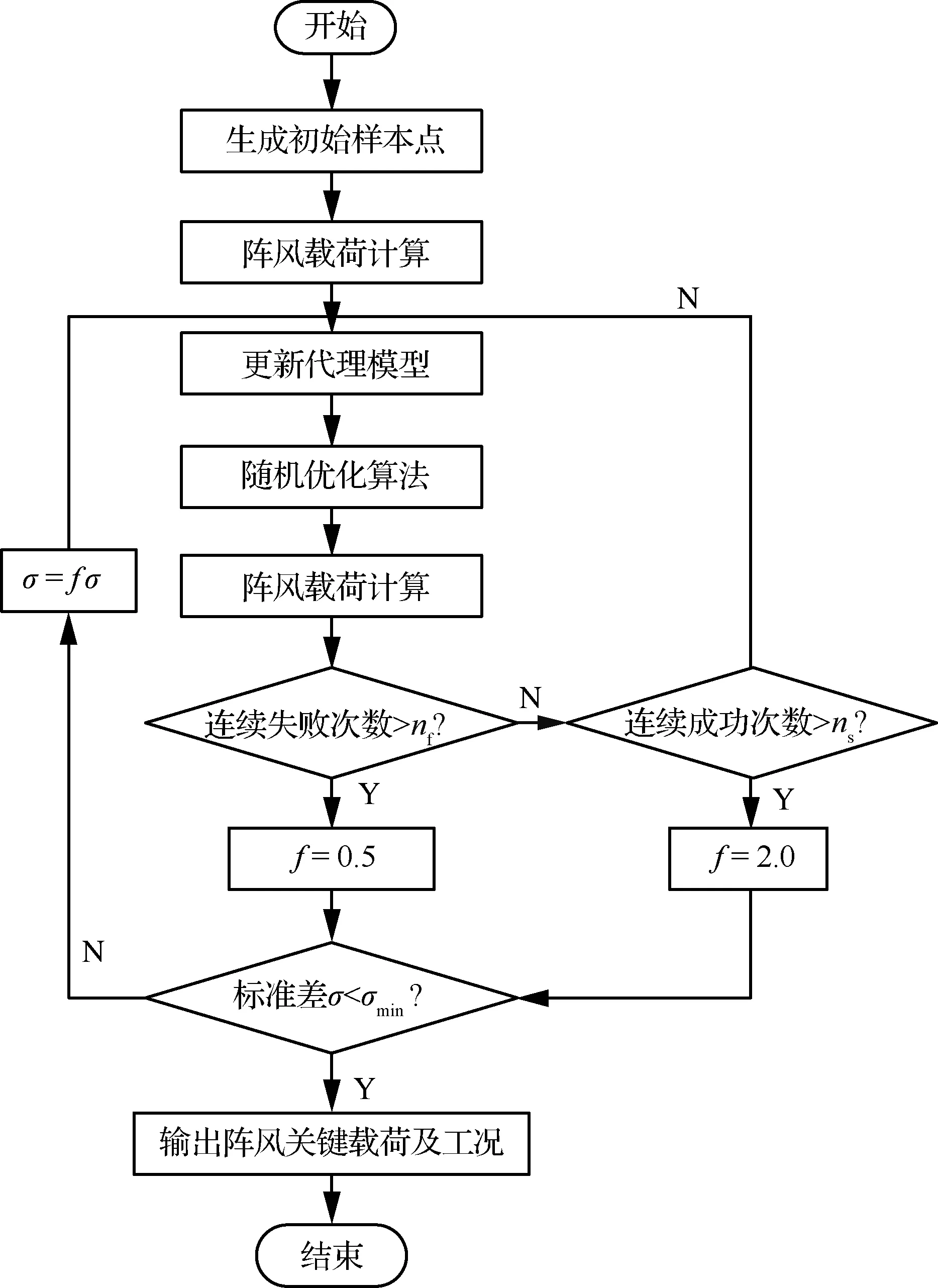
图3 阵风关键载荷的计算流程图Fig.3 Flow chart of computation of critical gust load

图4 模型外形示意图Fig.4 Schematic diagram of model’s shape表1 主要参数Table 1 Main parameters
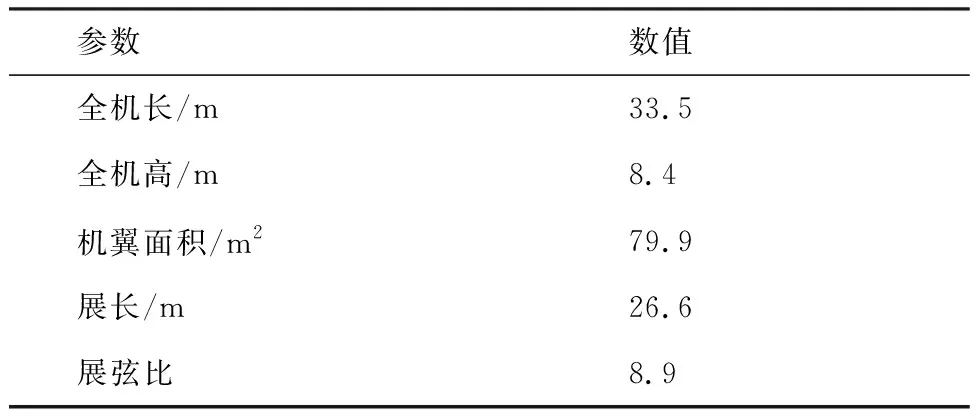
参数数值全机长/m33.5全机高/m8.4机翼面积/m279.9展长/m26.6展弦比8.9
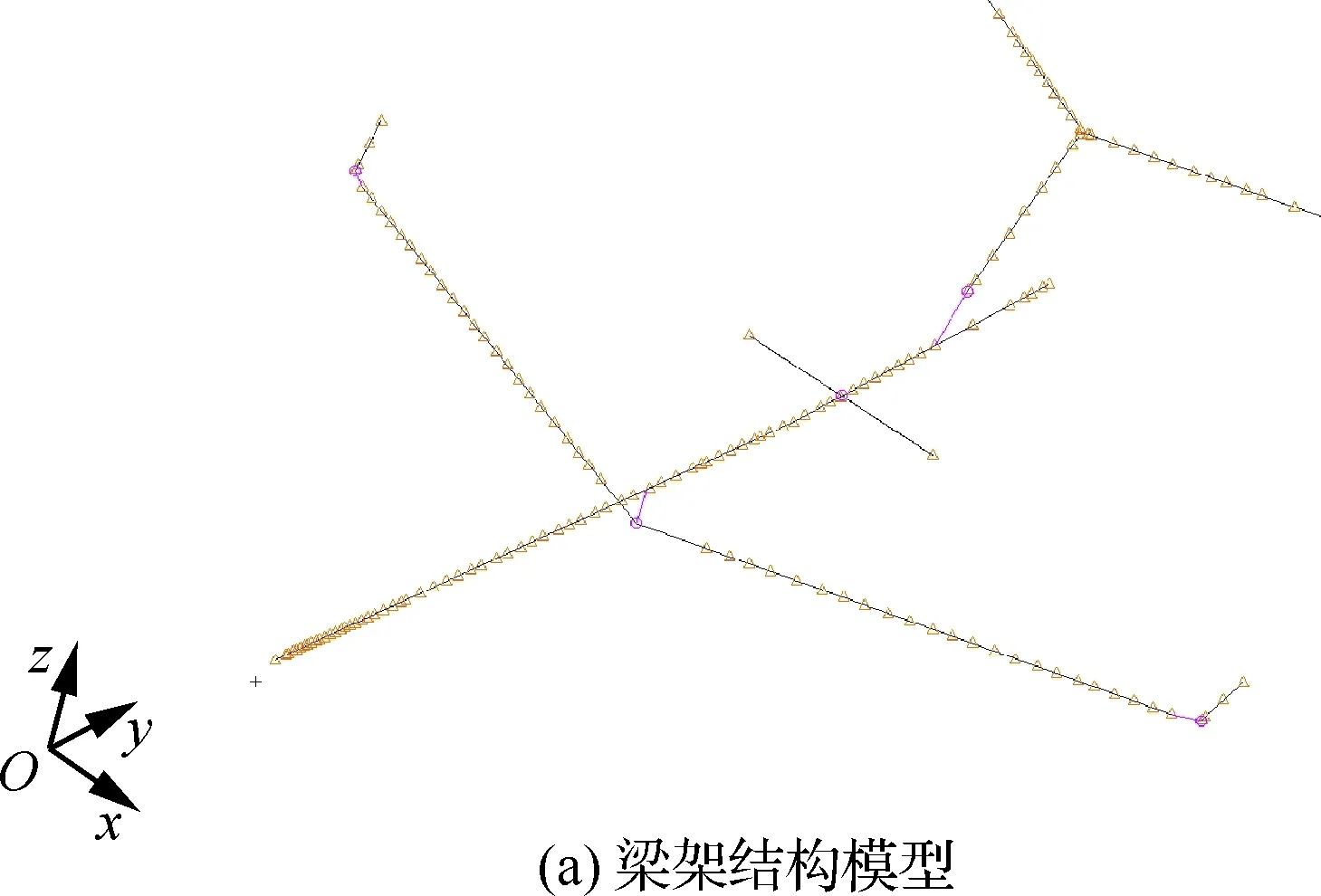
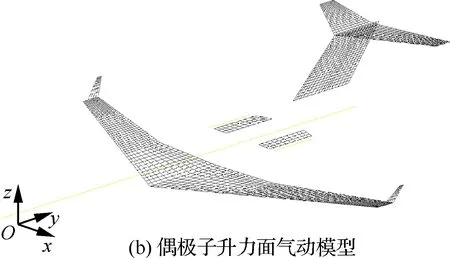
图5 阵风载荷计算模型示意图Fig.5 Schematic diagram of gust load computation model
在模态空间内进行阵风气弹耦合计算[10],控制方程为
(5)
式中:u为广义位移解;ω为圆频率;ρ和v分别为空气密度和速度;g为结构阻尼系数;M、C和K分别为广义质量矩阵、阻尼矩阵和刚度矩阵;Q为广义气动力系数矩阵;P为阵风引起的广义外部激励,其主要由阵风模型决定。本文计算采用适航条款规定的von Karman谱来定义阵风形状:
(6)
式中:w为阵风速度均方根值;L为阵风尺度;Ω为折算频率[10]。
计算模型中将飞行高度离散为0~12 000 m的8个特征高度(H0,H2,…,H7),速度离散为对应最大阵风强度的设计速度(V0)、设计巡航速度(V1)和设计俯冲速度(V2),飞行特征重量有最大设计起飞重量(C0)、最大设计着陆重量(C1)、最大设计零油重量(C2)、45 min余油重量(C3)4种,其各高度的重量分布已经充分考虑燃油的消耗逻辑,另外还有前重心(G0)、后重心(G1)2种不同的重心分布,构成192个阵风计算工况,如表2所示,该工况集的载荷包络值作为本文关键载荷预测对比的基准值。

表2 计算参数Table 2 Parameters for computation
2.2 方法验证
针对3个感兴趣的站位载荷进行对比分析,分别为机头、机身(机翼连接处)和垂尾根部,如图6 中黑色六角形所示,主要关心的载荷为以均方根值表示的增量弯矩、剪力以及扭矩。计算中最大标准差值σmax设置为0.02,最小标准差值σmin设置为0.005,nf和ns分别为5和3。
图7给出了机头无量纲弯矩收敛曲线,其中以机头处的弯矩基准值作为无量纲参数,从图中可以看出,虽然机头弯矩量值较小,但是本文建立的方法依旧可以找出关键工况,另外,采用Box-Behnken迭代次数比2LFF采样要多,表明对现行阵风载荷计算,采用2LFF选取初始样本点具有较大的优势。
图8给出了机身无量纲弯矩收敛曲线,对于机身机翼连接处,其弯矩具有较大的量级,2种方法都可以找到该站位的关键工况,其中Box-Behnken相对迭代次数较多,对于2LFF来说,其样本点恰巧包括了关键载荷工况,但本文优化模型计算依旧进行了若干次迭代,直至标准差达到收敛阈值σmin。图9给出了垂尾根部无量纲扭矩的收敛曲线,从图中可以看出,与机身类似,Box-Behnken收敛需要较多迭代,2LFF相对优势较为明显。
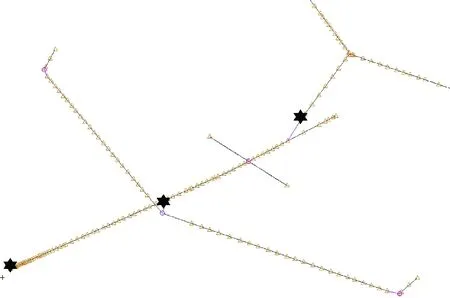
图6 站位示意图Fig.6 Schematic diagram of stations
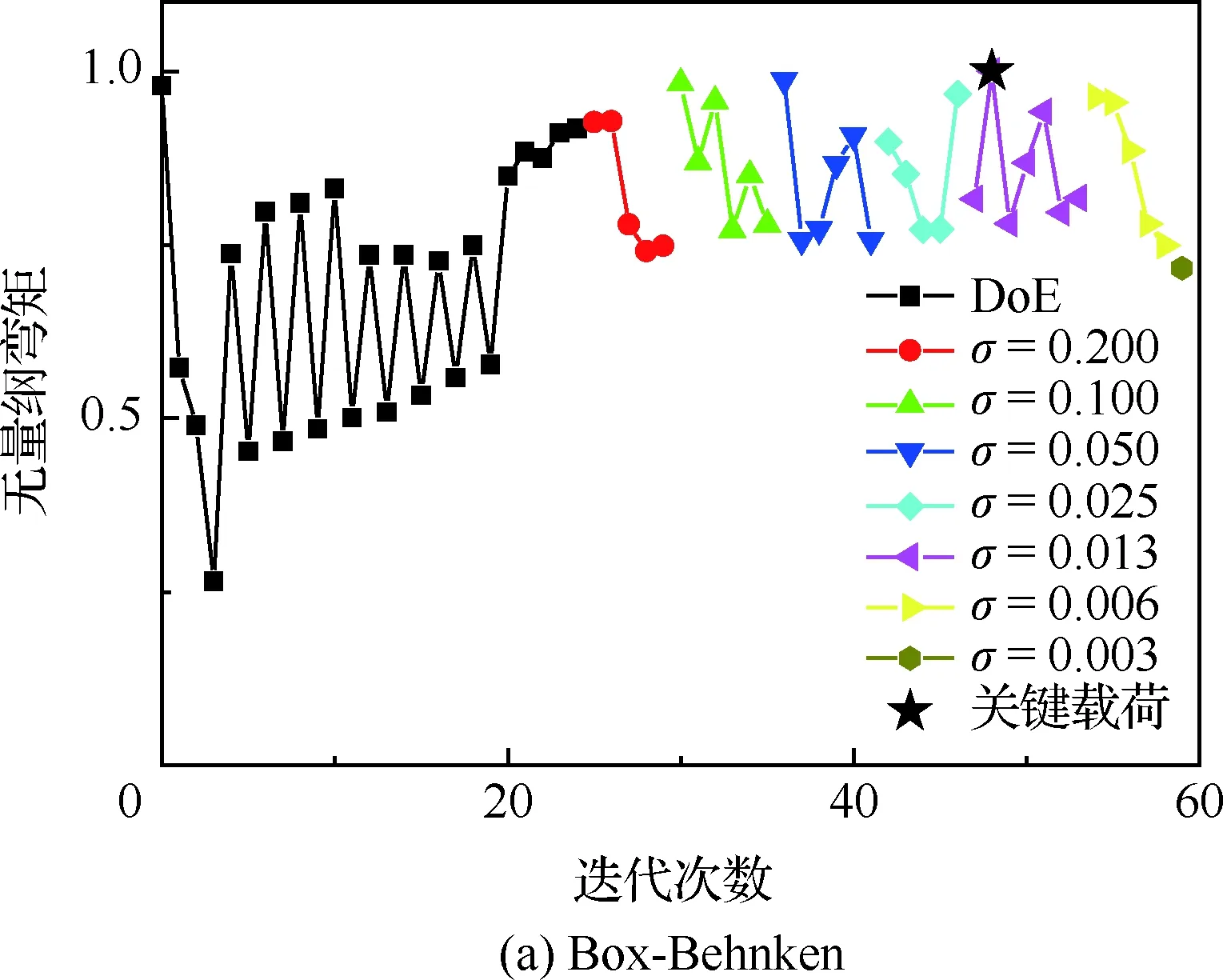
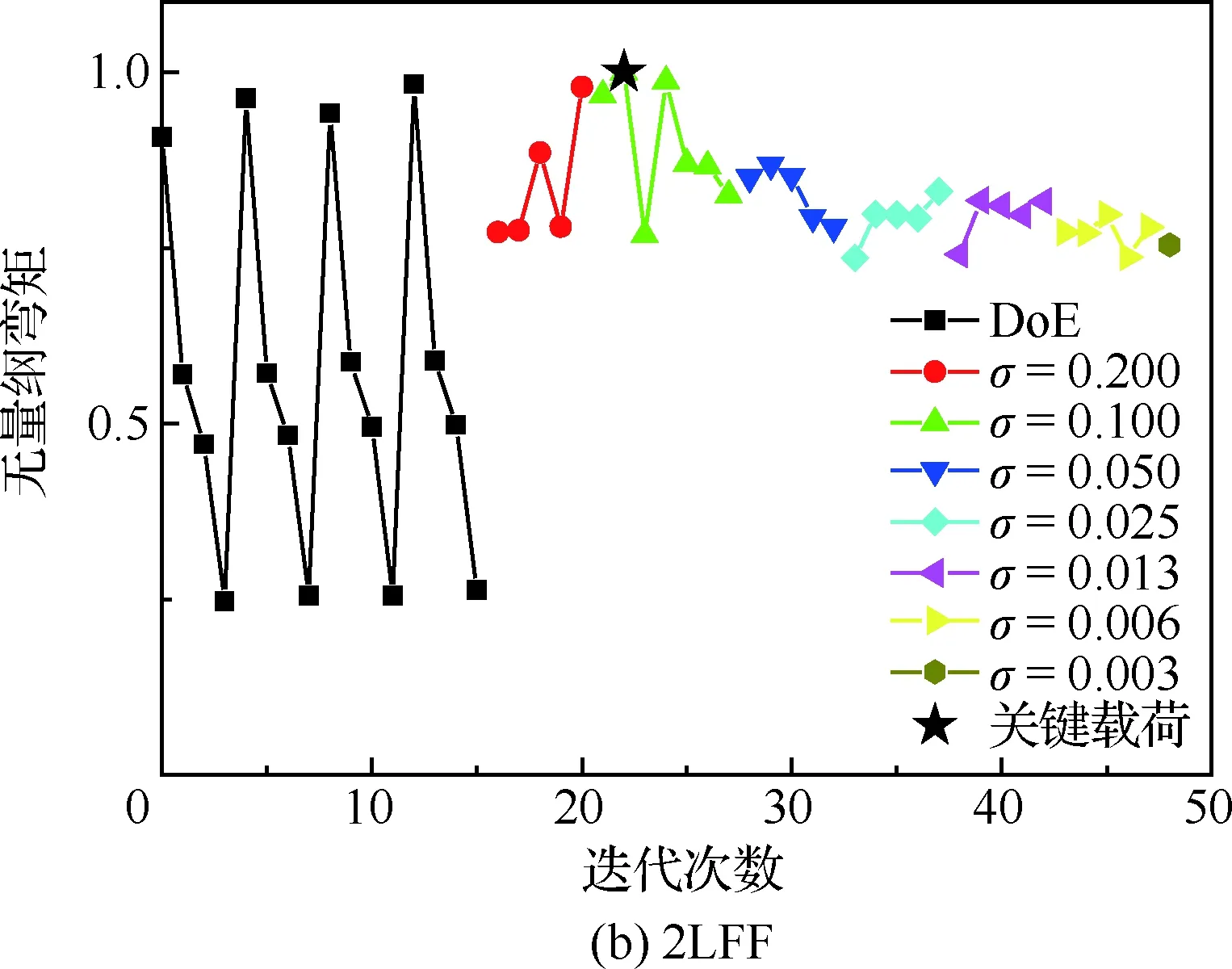
图7 机头无量纲弯矩收敛曲线Fig.7 Convergence curve of dimensionless bending moment of nose
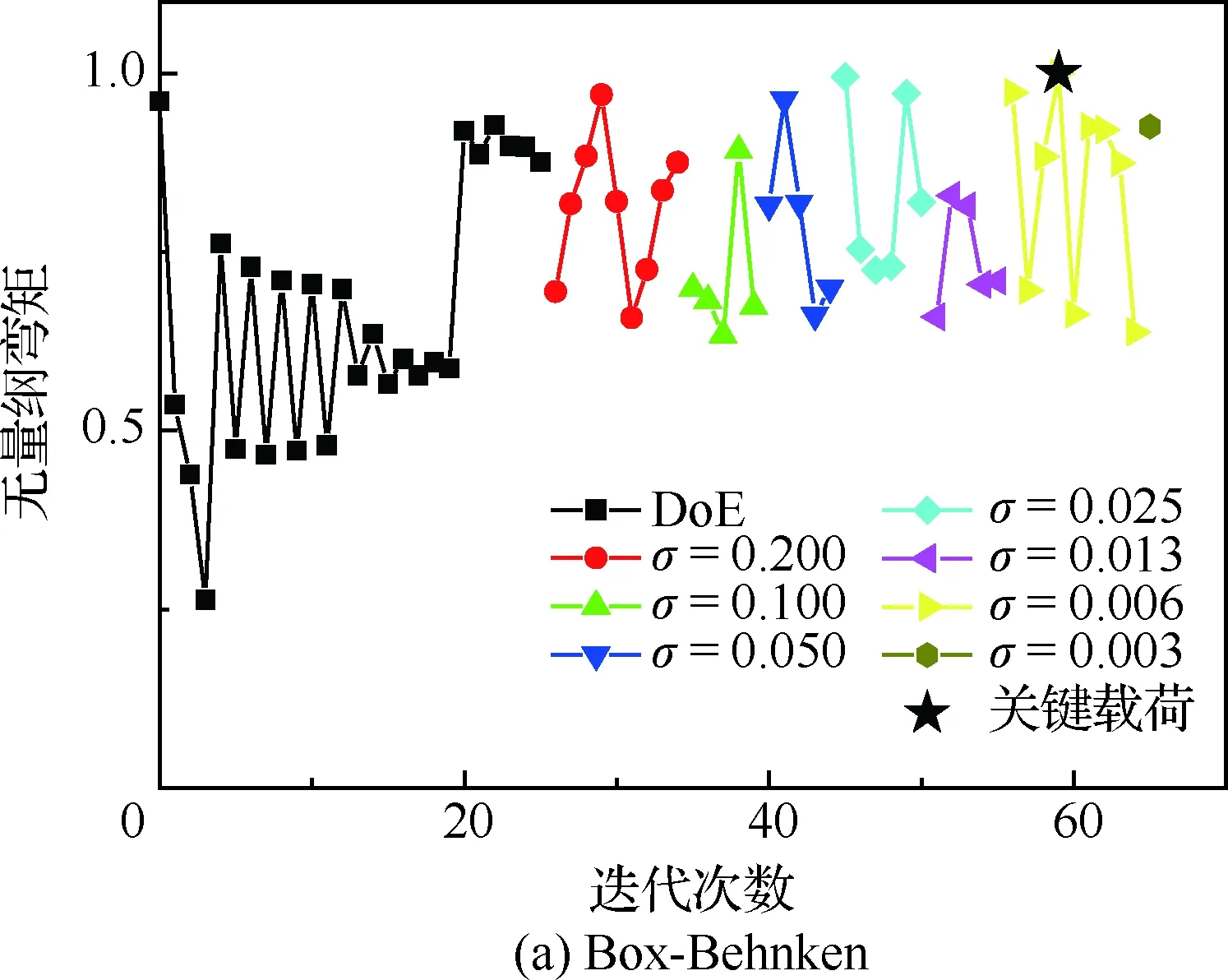
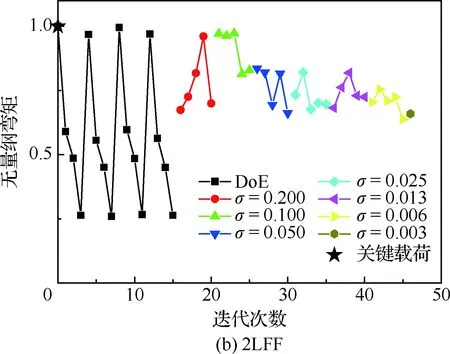
图8 机身无量纲弯矩收敛曲线Fig.8 Convergence curve of dimensionless bending moment of mid-airframe
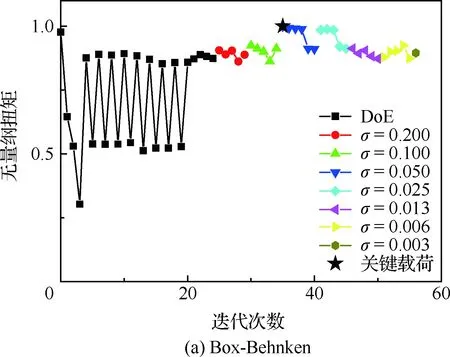
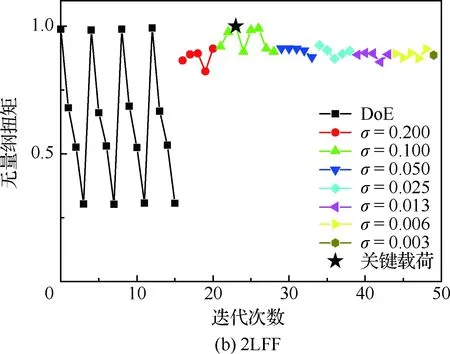
图9 垂尾根部无量纲扭矩收敛曲线Fig.9 Convergence curve of dimensionless root torque of vertical tail
3 参数评估
3.1 代理模型评估
下面对收敛后的代理模型MARS-2LFF进行评估。首先给出机身弯矩结果,如图10所示,其中黑色网格为实际模型计算得到的基准值,绿色直线为代理模型计算得到的值,蓝色点为代理模型构建所取的点,C1G0表示在最大设计着陆重量、前重心的组合下,载荷随速度、高度的变化。从图10可以看出,除个别边界点外,本文采用MARS方法构建的代理模型一定程度上可以模拟真实物理模型的特性,同时本文方法可以准确地寻找确定最大载荷值,而对于边界及外部点的预测,现有代理模型都不可避免地存在问题,本文方法同样不例外。
图11给出了垂尾根部扭矩代理模型与基准值对比结果,从图中可以看出,代理模型与基准值同样吻合得较好,同时结合图10(c)与(d)可以看出,连续阵风载荷的量值受特征重量参数的影响较弱,其很大程度上取决于飞行高度与速度。
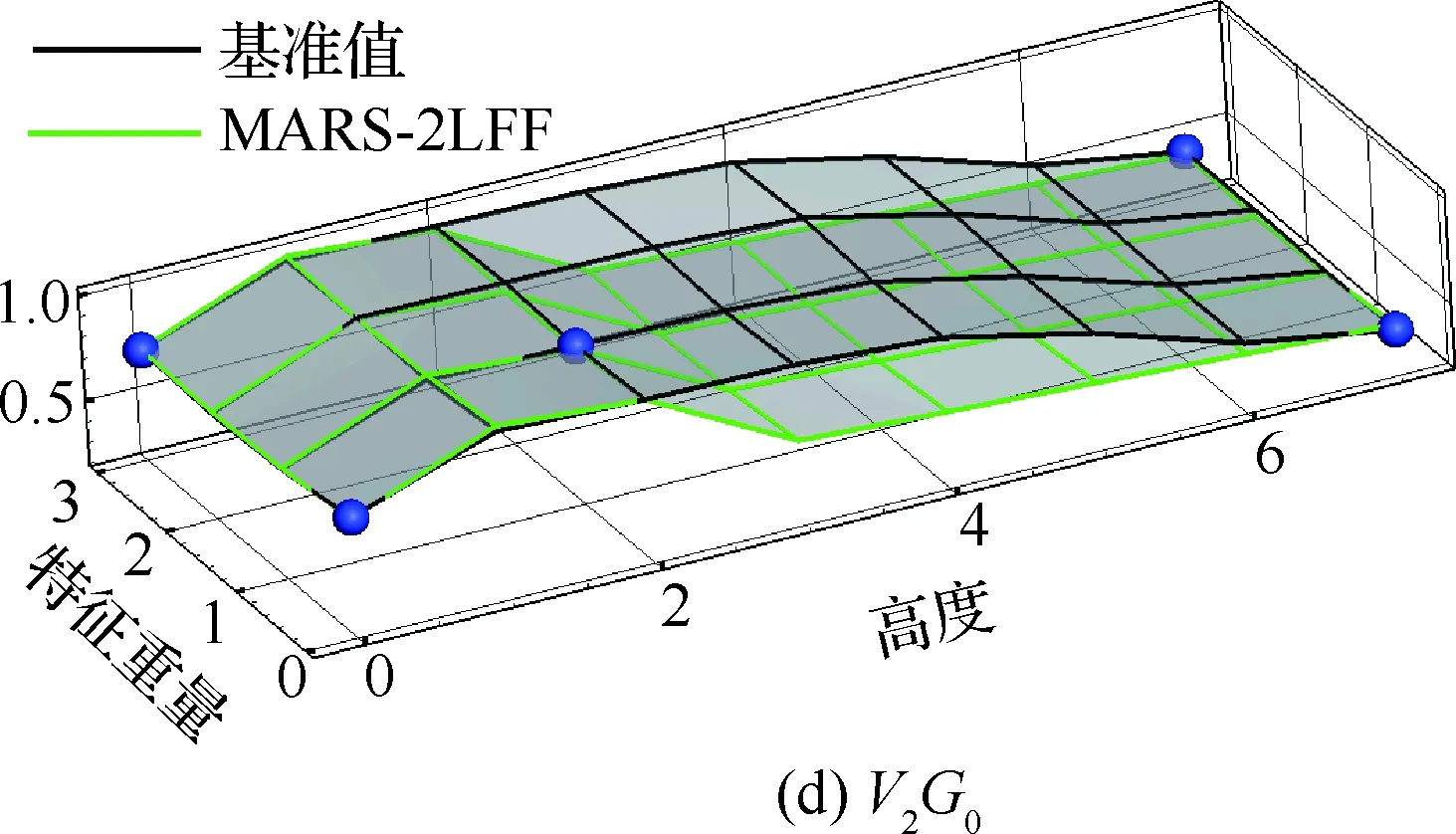
图10 机身弯矩代理模型评估Fig.10 Evaluation of bending moment of mid-airframe

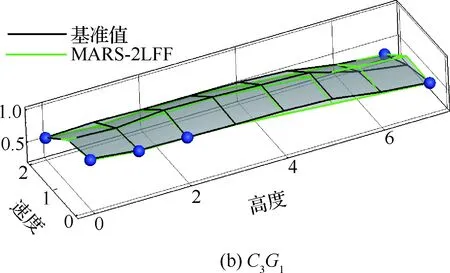
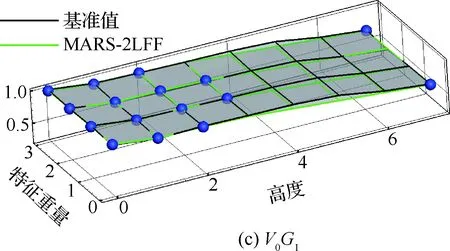
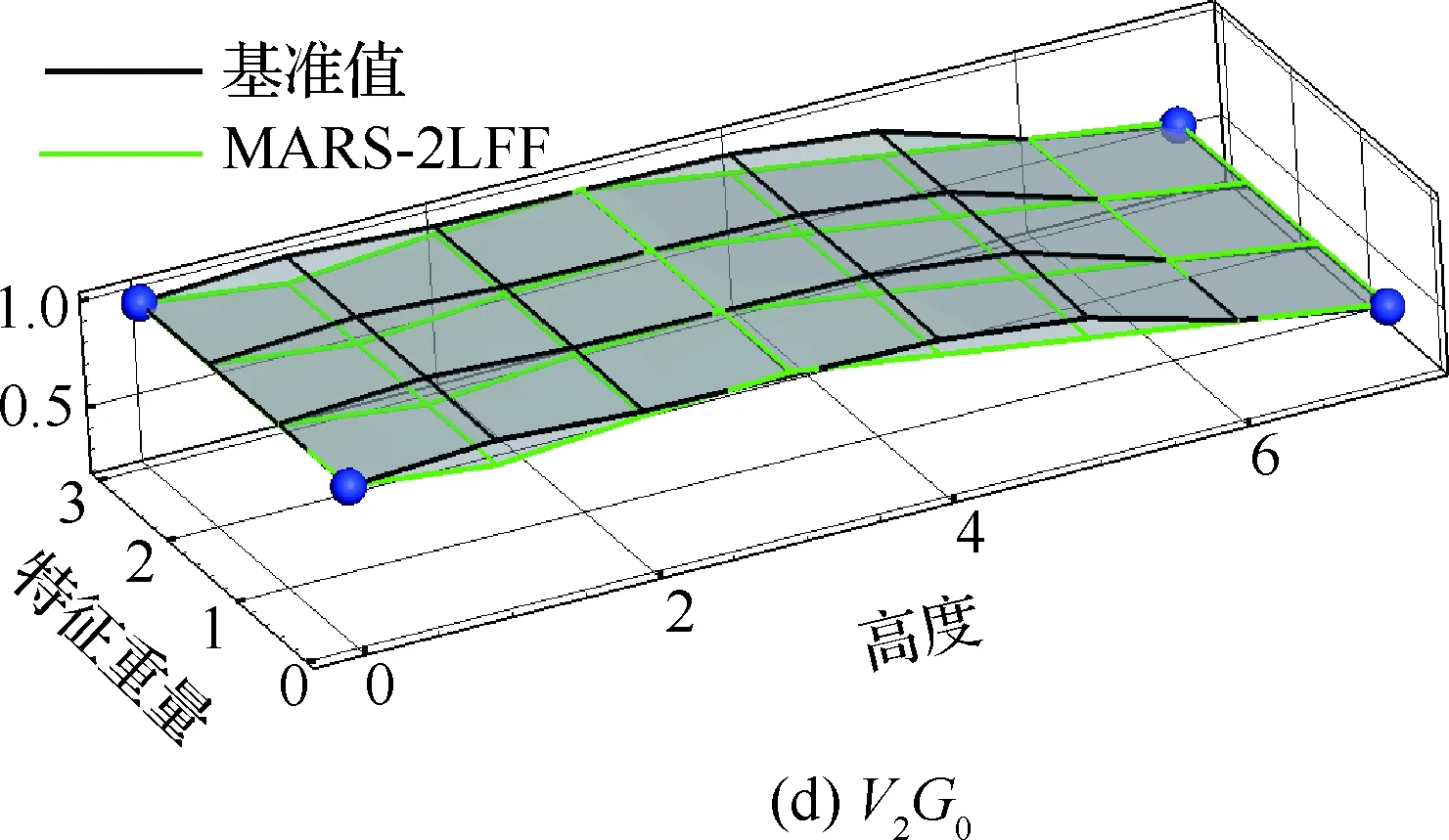
图11 垂尾根部扭矩代理模型评估Fig.11 Evaluation of root torque of vertical tail
图12和图13给出MARS-2LFF预测值与基准值的相关性对比图,分别对应192种工况的机身及垂尾根部弯矩和剪力。相比之下,垂尾的预测结果较好,这可能是由于垂尾根部受载情况相对简单,而机身与机翼连接处环境相对复杂。另外,由于MARS模型构建过程中为提高泛化能力进行了后向过程,因此对于关键工况及附近载荷预测同样存在误差,但是偏差总体较小。
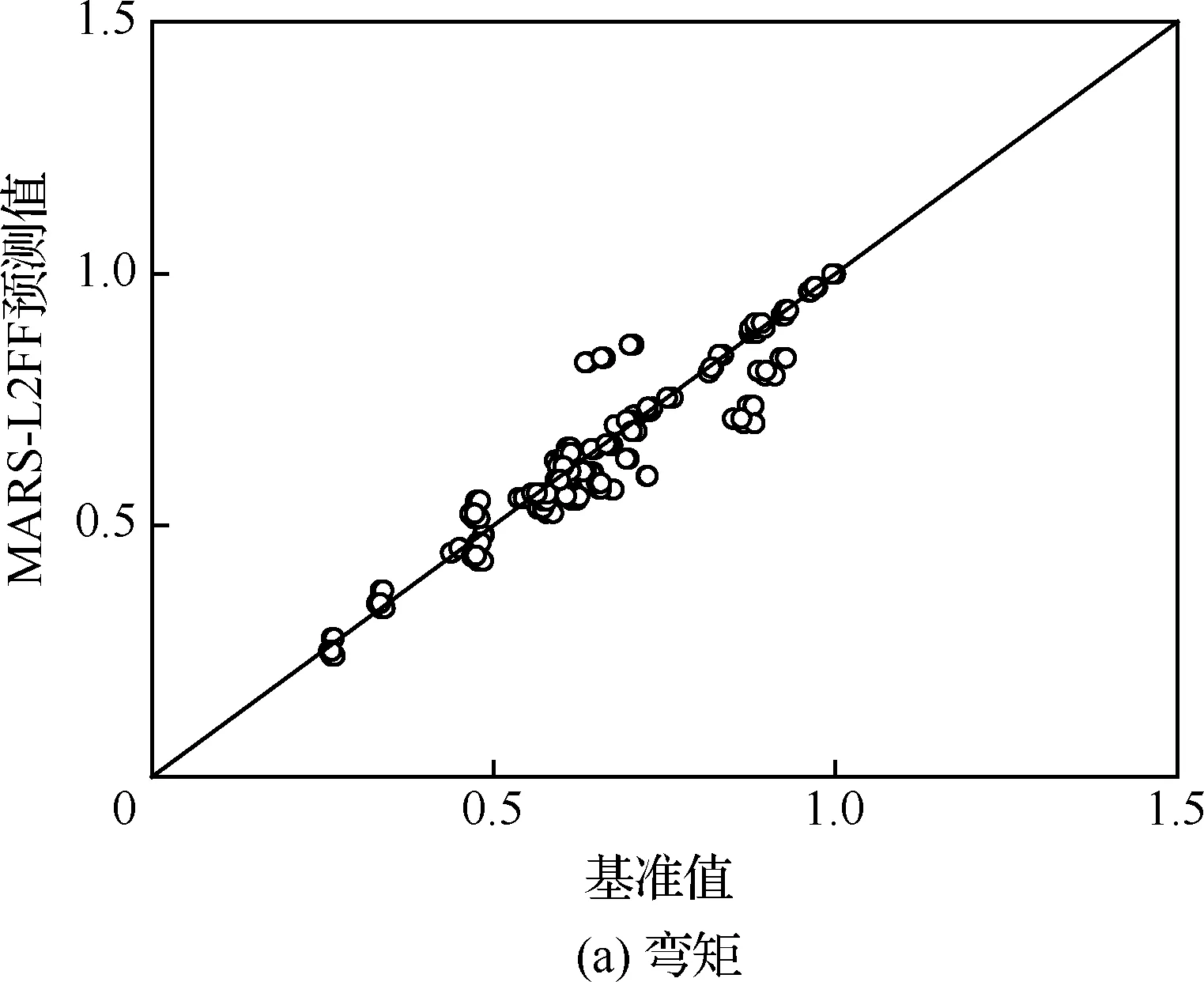
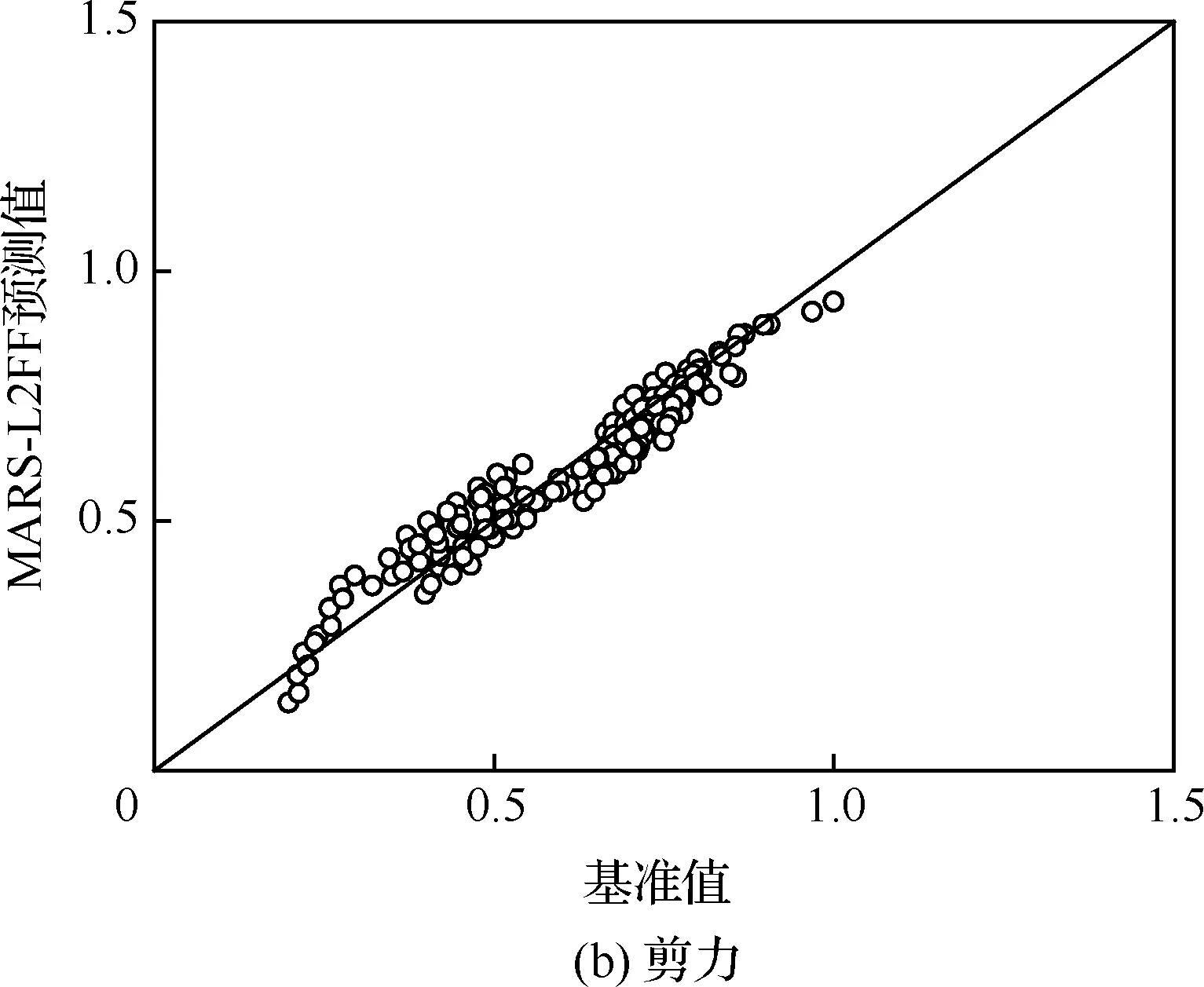
图12 MARS-2LFF代理模型相关性(机身)Fig.12 Correlation plot of MARS-2LFF surrogate model(mid-airframe)
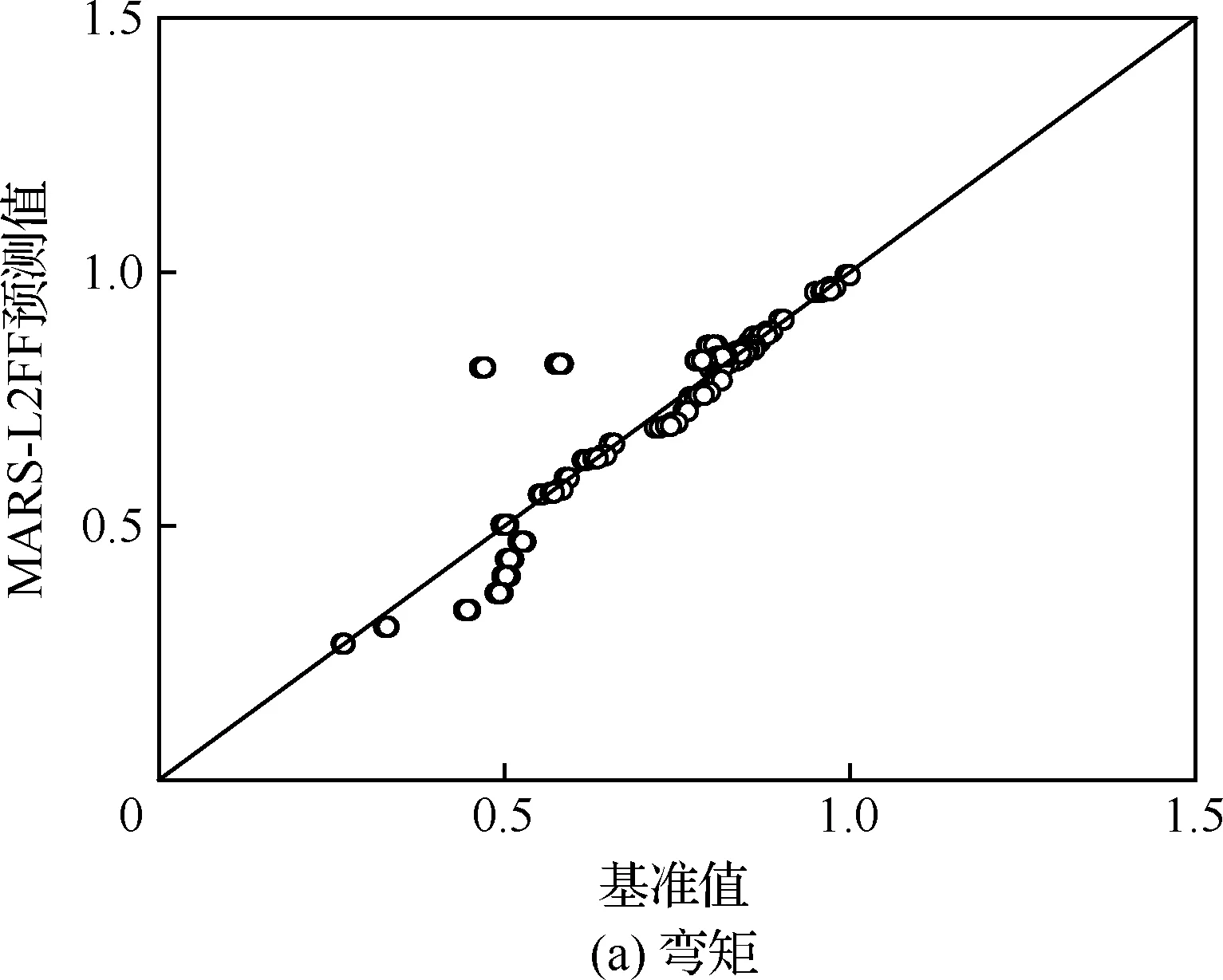
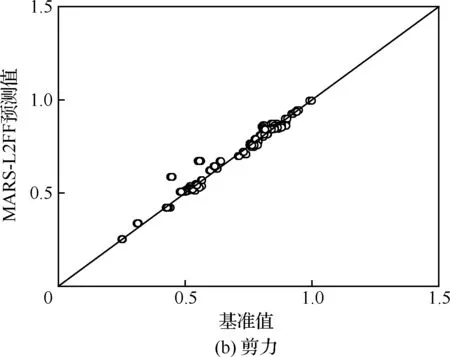
图13 MARS-2LFF代理模型相关性(垂尾)Fig.13 Correlation plot of MARS-2LFF surrogate model(vertical tail)
3.2 收敛性评估
针对自适应随机优化算法,并结合本文建立的侧向连续阵风气弹模型,进行参数影响的研究。模型涉及到参数主要有4个,分别是影响搜索半径的标准差最大值σmax、最小值σmin以及2个自适应参数ns、nf。
表3~表6给出了机身、垂尾根部扭矩随参数的变化规律。由表3~表6可知,一方面,本文模型可以较准确地预测关键工况及其载荷,即使设置标准差最大值、最小值相同,即仅进行一次图3 中的自适应循环,误差最大也仅为0.8%,且分布在对角线附近,这表明模型的准确性只取决于σmax与σmin的相对倍数,其绝对值对结果影响较小。另一方面,自适应参数ns和nf的减小一定程度上可以降低总迭代次数,而对精度影响较小。同时,针对本文模型,最多56次的工况迭代即可得到准确的关键载荷,相对工程实际的192次计算效率至少提升70%。
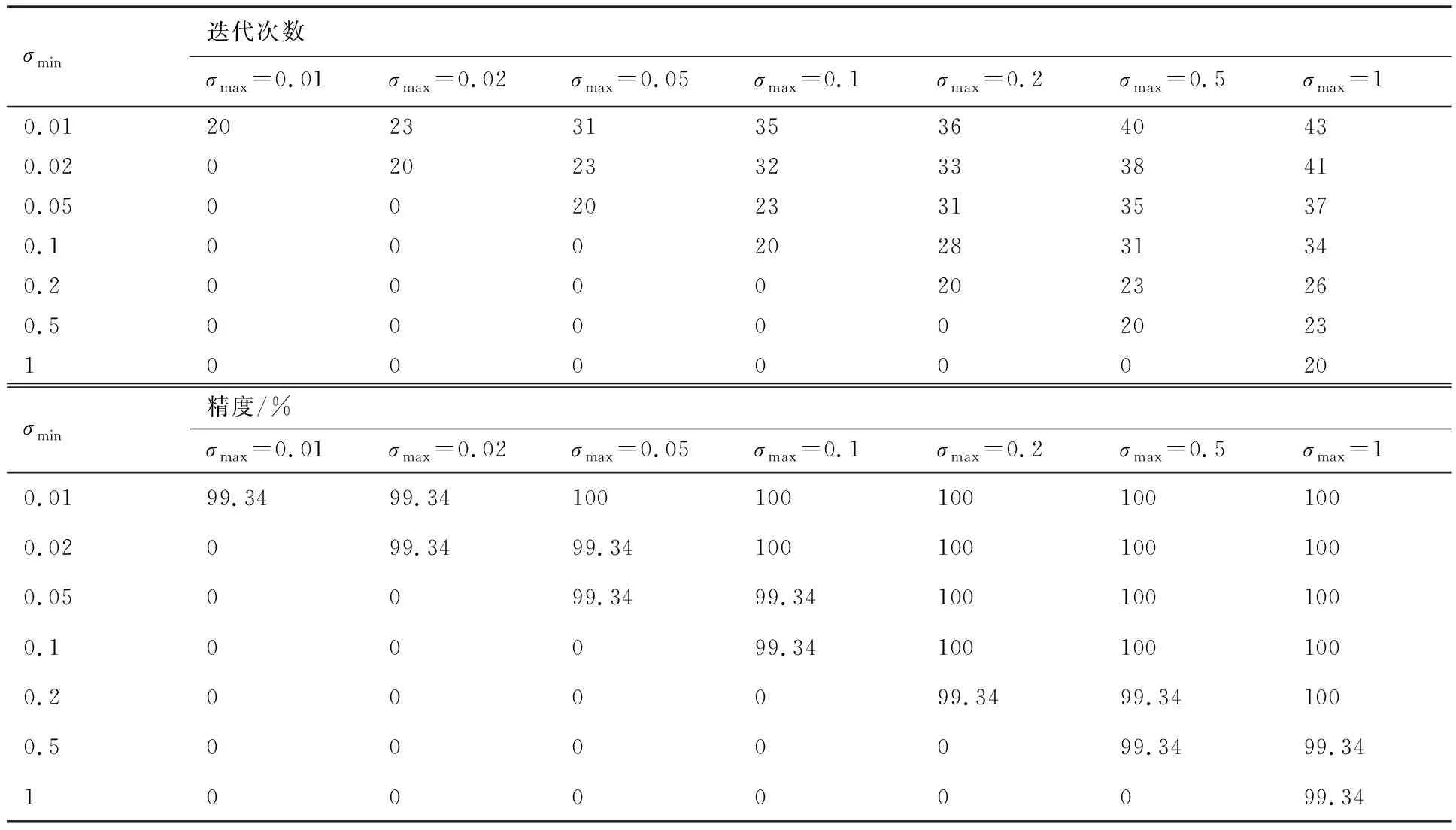
表3 标准差对机身扭矩预测影响(ns=1,nf=3)Table 3 Influence of standard deviation on prediction of mid-airframe torque (ns=1,nf=3)
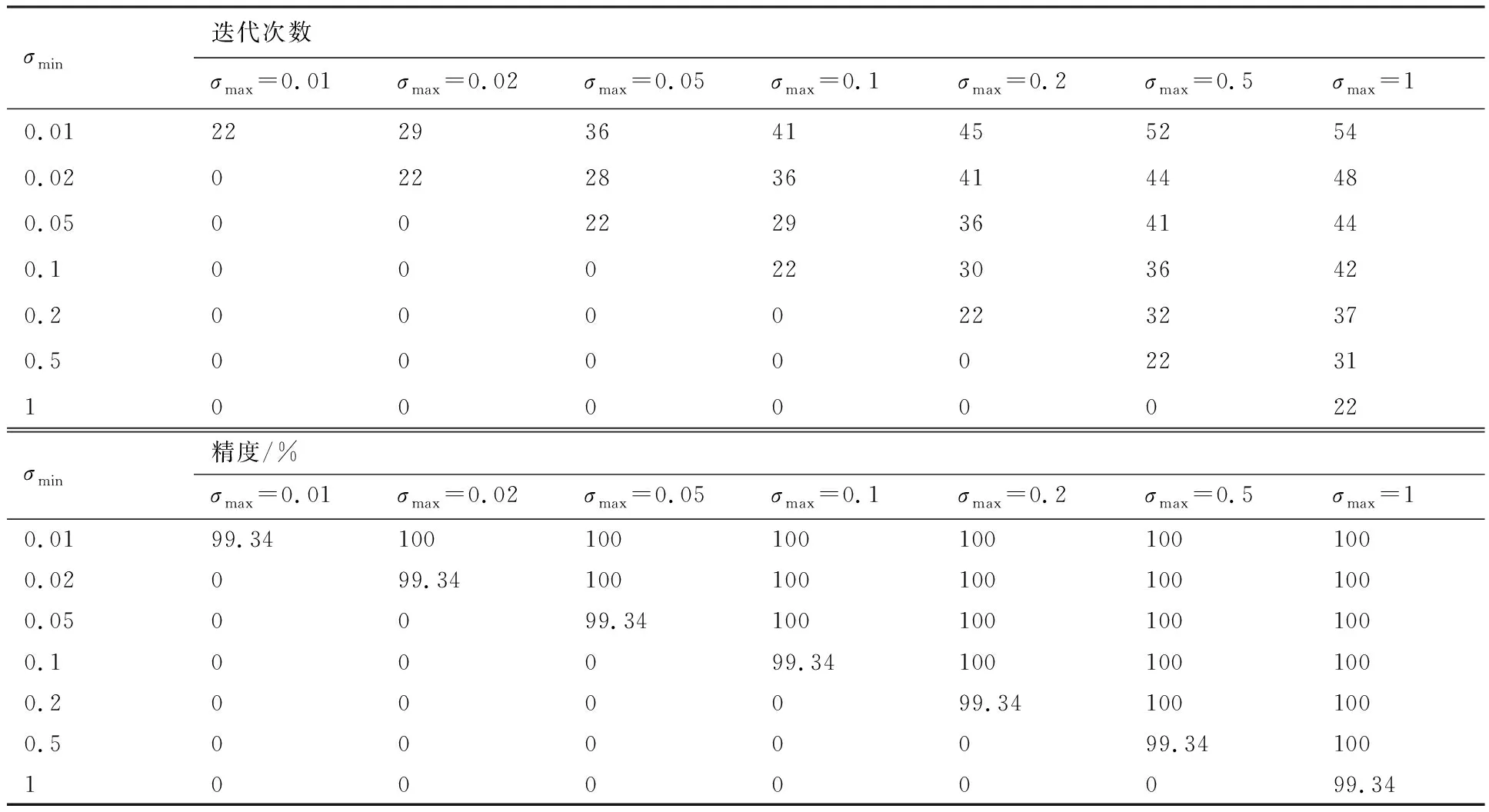
表4 标准差对机身扭矩预测影响(ns=3,nf=5)Table 4 Influence of standard deviation on prediction of mid-airframe torque (ns=3,nf=5)
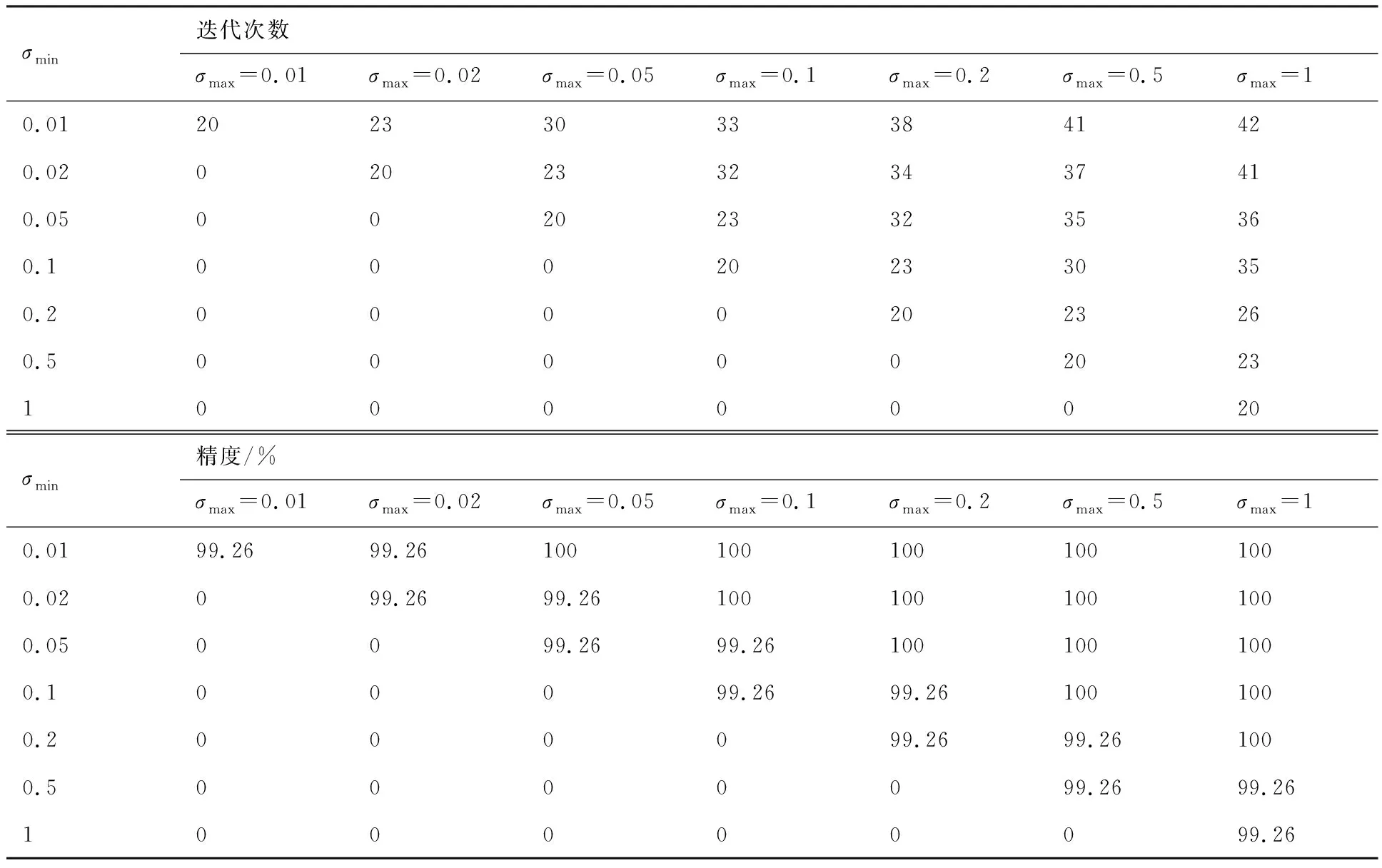
表5 标准差对垂尾根部扭矩预测影响(ns=1,nf=3)Table 5 Influence of standard deviation on prediction of vertical tail root torque (ns=1,nf=3)
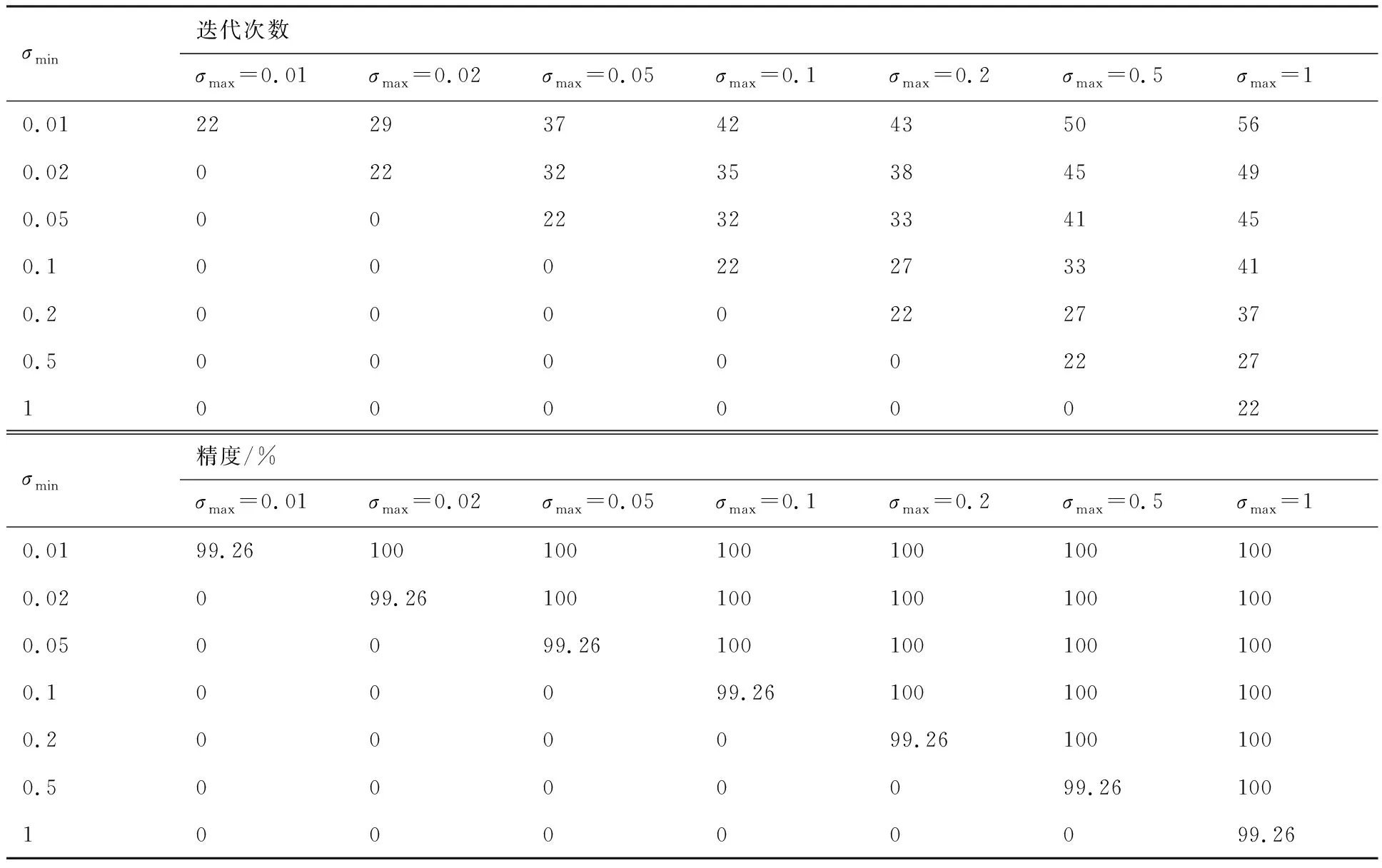
表6 标准差对垂尾根部扭矩预测影响(ns=3,nf=5)Table 6 Influence of standard deviation on prediction of vertical tail root torque (ns=3,nf=5)
表7给出了采用参数σmin=σmax=1、ns=1、nf=3预测得到的结果,虽然该参数迭代次数较少,但仍可成功实现对高度(H)、速度(V)和重心位置(G)的准确识别,仅对特征重量项(C)的预测错误,即便如此,扭矩误差值也在1%以内。
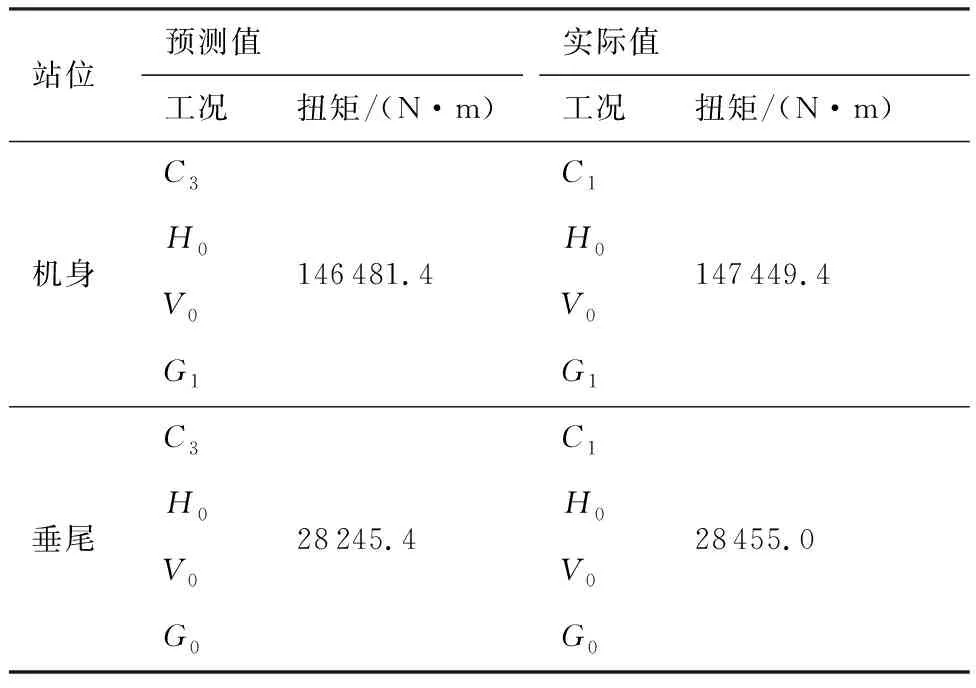
表7 关键工况及载荷对比Table 7 Comparisons of critical cases and loads
4 结 论
本文采用2LFF采样技术结合MARS方法,建立了一个可进行快速预测的代理模型,并基于自适应随机优化算法,发展了一套阵风关键工况及载荷的主动识别预测方法,并以某型民机侧向连续阵风计算模型为例,进行了验证,同时对所建立算法各参数的影响进行了深入的研究,结果表明:
1) 2LFF采样相对于其他DoE方法可更有效地用于目前阵风载荷代理预测模型的构建。
2) 采用MARS构建的代理模型,结合自适应随机优化算法可有效地识别阵风关键工况及载荷,可有效避免大量不必要工况的计算从而显著提高效率。
3) 自适应参数对预测精度影响较小,适当减小可以有效地降低总迭代次数。
