基于并行模型自适应滤波的空间目标相对位姿估计*

熊 凯，魏春岭，辛优美

1. 北京控制工程研究所,北京 100094;2.空间智能控制技术国家级重点实验室,北京 100094.

0 引 言

作为典型的非线性系统信息融合方法，扩展卡尔曼滤波(EKF)及其改进算法在航天器自主导航和姿态确定中得到广泛应用[1-2]，并已形成标准化算法.在EKF算法设计过程中，通常假设模型中的系统噪声和测量噪声方差是精确已知的.然而，在工程实践活动中，受应用条件和环境因素的影响，这一假设往往得不到满足.对于本文所研究的空间目标相对位姿确定系统，通过观察卫星上的双目立体视觉相对导航敏感器指向目标卫星进行观测，受观察卫星平台姿态抖动和空间光照条件等因素的影响，敏感器误差特性往往会发生变化，此时，测量噪声方差会偏离通过地面测试获得的标称值.对于测量噪声统计特性的变化，传统EKF算法不具备自适应能力.在实际敏感器测量噪声方差不同于其标称值的情况下，会导致EKF性能下降.

针对噪声统计特性不确定性的影响，以往研究中已给出多种策略，主要目的是增强滤波算法的自适应能力.举例来说，鲁棒扩展卡尔曼滤波(REKF)基于噪声方差的上界进行设计，但是，基于先验信息选定的噪声方差上界往往具有某种保守性，不利于提升滤波器的估计精度.多模型滤波采用一种更为精巧的方式描述噪声统计特性不确定性的影响[3]，具体方法是基于多个不同的噪声方差阵建立多个模型，并基于各个模型分别设计并行滤波器，各个滤波器实施并行计算，最终的状态估计结果是各个并行滤波器状态估计值的加权和.该方法的局限性体现在，为了全面覆盖噪声方差的取值范围，往往需要建立一个庞大的模型集构成空间网格，相应地，需要设计大量的并行滤波器并同时实施解算，较重的计算负担限制了该方法的应用范围.

近些年来，具有噪声统计特性在线估计能力的自适应滤波算法得到广泛重视[4-5].对于线性时不变系统、线性时变系统和非线性系统，分别给出了多种不同方法，包括自适应卡尔曼滤波(AKF)[6]、自适应扩展卡尔曼滤波(AEKF)[7]、自适应无迹卡尔曼滤波(AUKF)[8]，以及自适应鲁棒平方根容积卡尔曼滤波(ARSCKF)[9-10]等.对于噪声统计特性未知的情况，应用以AEKF为代表的自适应滤波算法能够取得较好的效果.但是，在噪声统计特性已知的情况下，受噪声方差在线估计误差的影响，AEKF的性能往往不及传统EKF.

空间目标相对位姿确定系统的敏感器测量噪声方差的标称值可通过地面测试得到，但对于部分应用场景，实际敏感器测量噪声方差会偏离其标称值.针对上述问题，本文基于特定的自适应率将EKF和AEKF结合起来，设计了一种并行模型自适应滤波(PMAF)算法，该方法在测量噪声统计特性不确定性存在和不存在两种情况下，均能取得较好的状态估计结果.

本文内容安排如下：首先，针对带有统计特性不确定性的非线性状态空间模型，设计了PMAF方法；其次，给出了空间目标相对位姿确定系统的数学表达式；进而，展示了对比研究和仿真分析的结果.

1 并行模型自适应滤波

考虑如下所示的离散时间非线性系统

xk=f(xk-1)+wk(1)

yk=h(xk)+vk(2)

其中，xk和yk分别为l维状态向量和m维观测向量，f(·)和h(·)是连续可微状态转移函数和测量函数，wk和vk分别为l维过程噪声和m维测量噪声.假定wk和vk为不相关的高斯白噪声，噪声统计特性为

(3)

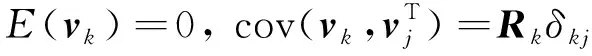
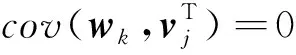
其中，Qk和Rk为正定对称阵，δkj为克拉姆尼克-狄拉克算子，当k=j时，其取值为1，其他情况下取值为0.假定系统噪声方差Qk是精确已知的，而测量噪声方差Rk在应用过程中可能会发生变化，其取值范围如下

(6)

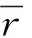
以往研究表明，对于测量噪声方差错误的取值会显著降低滤波性能.针对上述问题，提出一种基于EKF和AEKF并行计算的PMAF算法，两个并行滤波器各分配一个权值，通过设计自适应率调节权值的大小，将两个并行滤波器估计结果的加权和作为全局状态估计.基于上述设计，在测量噪声方差的真值等于标称值时，令EKF在状态估计中起主导作用，相反，在测量噪声方差的真值偏离标称值时，令AEKF起主导作用，从而扬长避短，充分发挥EKF和AEKF各自的性能优势.

(7)

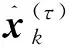
(8)

PMAF算法的迭代计算过程如下：

Step1.并行滤波

对于k∈{1,2,…,∞},两个并行滤波器分别对状态向量和估计误差方差进行预测和更新.状态预测基于系统模型进行

(9)

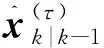
(10)

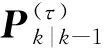
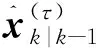
(11)

其中，

(12)

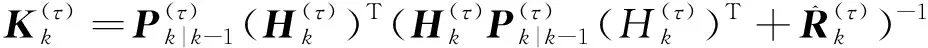
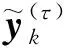
(14)

估计误差方差根据下式进行更新

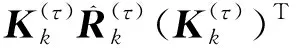
两个并行滤波器的主要区别体现在测量噪声方差的取值.对于第1个并行滤波器，测量噪声方差取标称值

(16)

对于第2个并行滤波器，通过滑动平均法对测量噪声方差进行在线估计

(17)

其中，

(18)

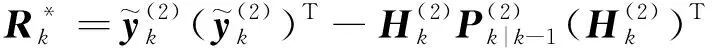
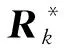
Step2.权值更新

利用测量新息更新两个并行滤波器的权值，并进行归一化.

(20)

其中，

(21)

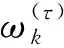
Step3.加权融合

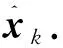
(22)

在权值收敛的情况下，PMAF的状态估计值近似等于其中一个并行滤波器的状态估计值.

所设计的PMAF算法结构可归纳如图1所示，其特色在于：能够自适应地在不同滤波算法之间进行切换或折衷，这使其在应对模型不确定性，或敏感器受环境影响测量特性发生变化时，能够体现出优于EKF或AEKF的性能水平.

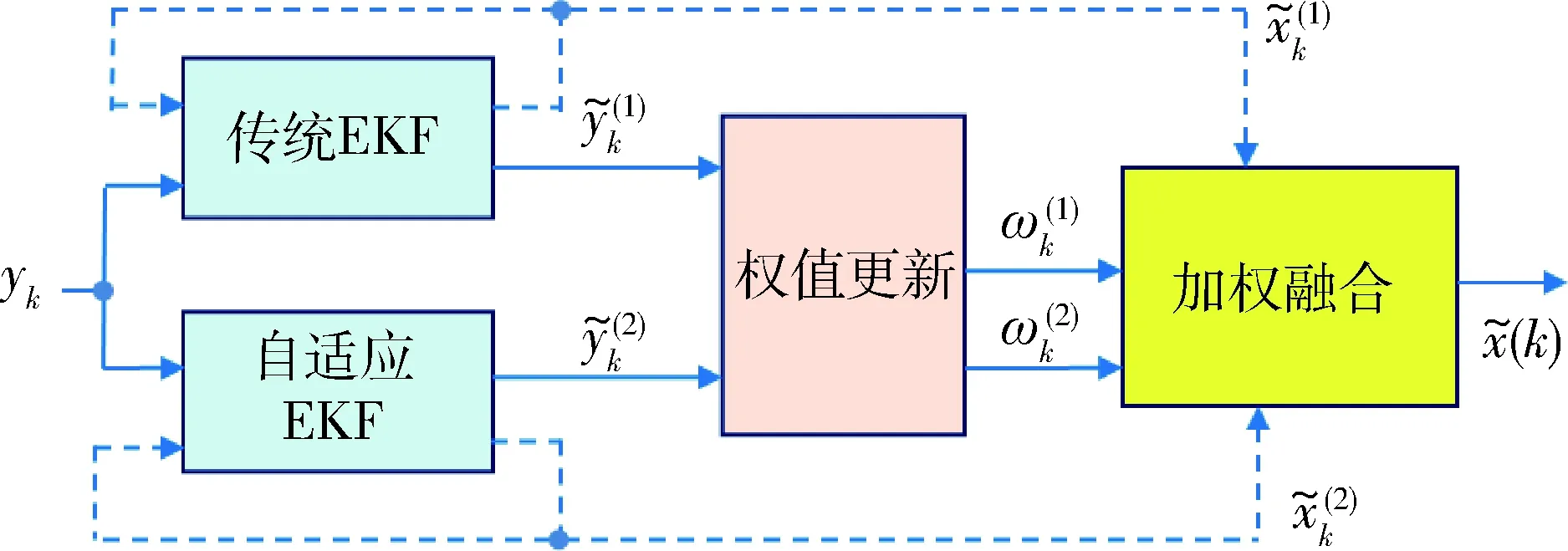
图1 并行模型自适应滤波算法结构示意图Fig.1 Structure of parallel-model adaptive filter algorithm

2 空间目标相对位姿确定

空间目标相对位姿确定系统能够提供目标卫星与观察卫星的相对姿态和相对位置信息，是空间操控任务成功的重要保障，基本方法是以敏感器获得的目标卫星特征点位置矢量信息作为观测量，以相对姿态、惯性角速度、相对位置和相对速度作为状态向量，利用相对导航滤波算法，结合轨道姿态动力学模型，对空间目标的运动状态进行估计.

系统的状态向量定义为

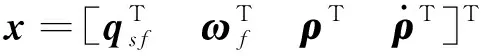
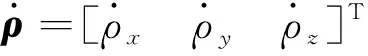
受篇幅所限，在此仅给出线性化后的系统误差方程[12]：

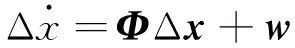
其中，

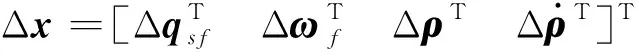
A(qsf)是根据四元数计算得到的从目标卫星体坐标系到观察卫星体坐标系的转换矩阵，矩阵中元素为姿态角速率的各个分量ωo是目标卫星的轨道角速率，Ix、Iy和Iz是目标卫星的惯量参数，w表示未建模噪声.

利用观察卫星上的双目立体视觉相对导航敏感器对目标卫星上的位置已知的特征点进行观测，测量方程可写为式(25)，相应的观测矩阵可参见文献[12]

(25)

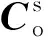
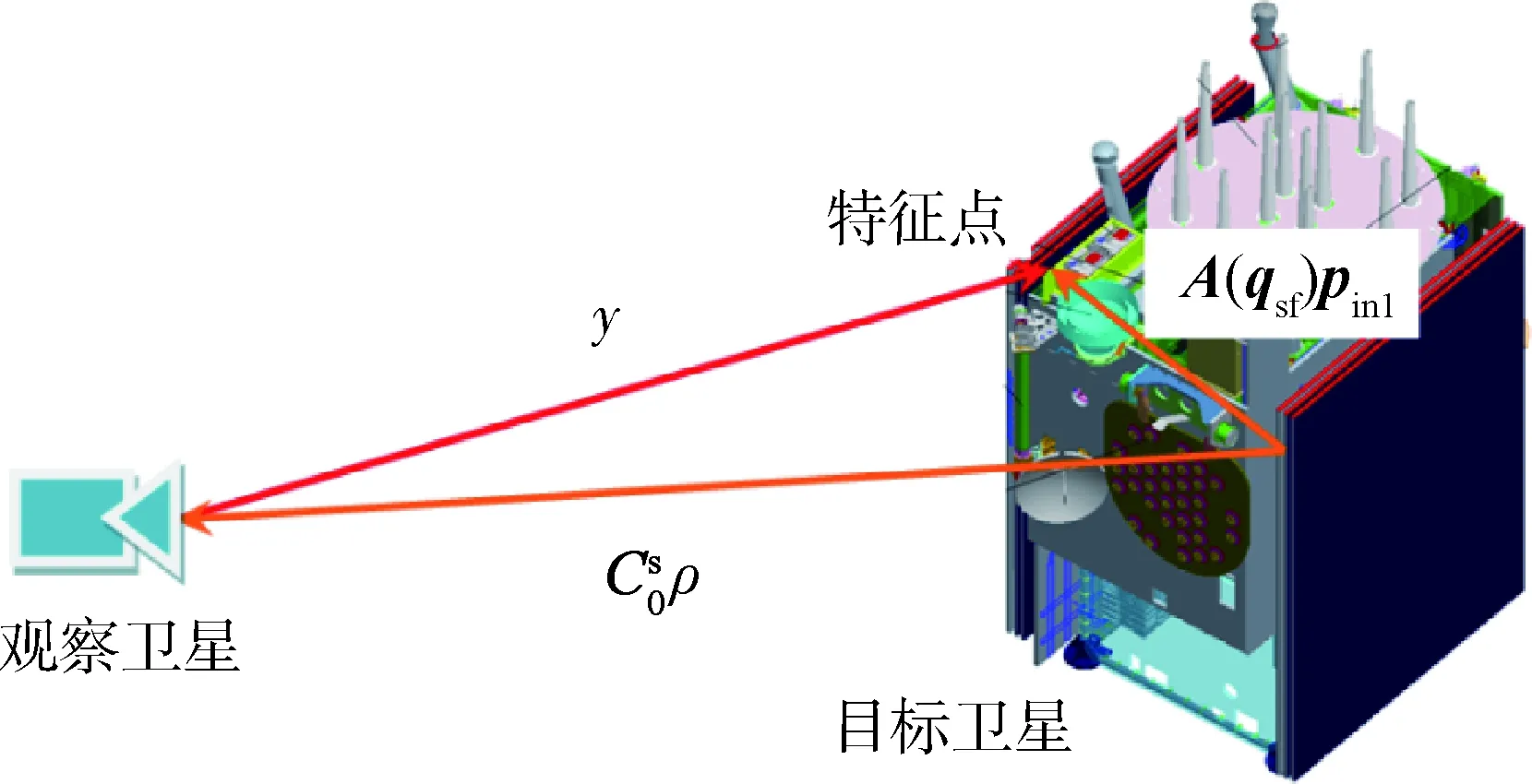
图2 特征点位置矢量测量示意图Fig.2 Position vector measurement of feature points

3 仿真结果

为了说明所提PMAF算法的有效性，通过仿真将其与EKF算法和AEKF算法进行了对比研究.目标卫星和观察卫星的真实运动状态通过高精度姿态轨道仿真器获得，根据真实运动状态数据和观测模型产生测量数据，利用EKF、AEKF和PMAF这3种不同的滤波方法对测量数据进行处理，产生状态变量的估计值.将状态变量的估计值与真实运动状态数据进行比对，得到状态估计误差.

假定目标卫星在半长轴为6 878 km、轨道倾角为98°的近圆轨道飞行，其惯量参数为Ix=100 kg·m2，Iy=100 kg·m2，Iz=200 kg·m2,特征点位置矢量在星体系的坐标为pin1=[1 0 0]Tm,pin2=[1 1 1]Tm,pin3=[0 1 0]Tm,pin4=[-1 1 -1]Tm.观察卫星在距离目标卫星100 m左右位置形成自然绕飞，双目立体视觉相对导航敏感器的测量精度为1 cm，数据更新频率为1 Hz.

为了公平起见，三种滤波算法中取同样的初始误差方差及系统噪声方差.测量噪声方差的标称值为pk=(0.01 m)2I12×12,AEKF中选择参数LR=100,权值更新过程中，选择矩阵Sk=Rk.

下面分两种不同情况进行仿真.

Case1：测量噪声方差的真值等于标称值

基于不同的随机噪声进行20次仿真，得到EKF、AEKF和PMAF的三轴相对姿态估计误差均方根的范数，如图3所示，相应地，两个并行滤波器的权值变化曲线如图4所示.从图中不难看出，不存在模型不确定性的情况下，PMAF的性能优于AEKF，原因在于PMAF中的第1个并行滤波器不会受到测量噪声方差估计误差的影响.基于EKF设计的并行滤波器权值收敛于1，在总体状态估计中起主导作用，结果符合预期.

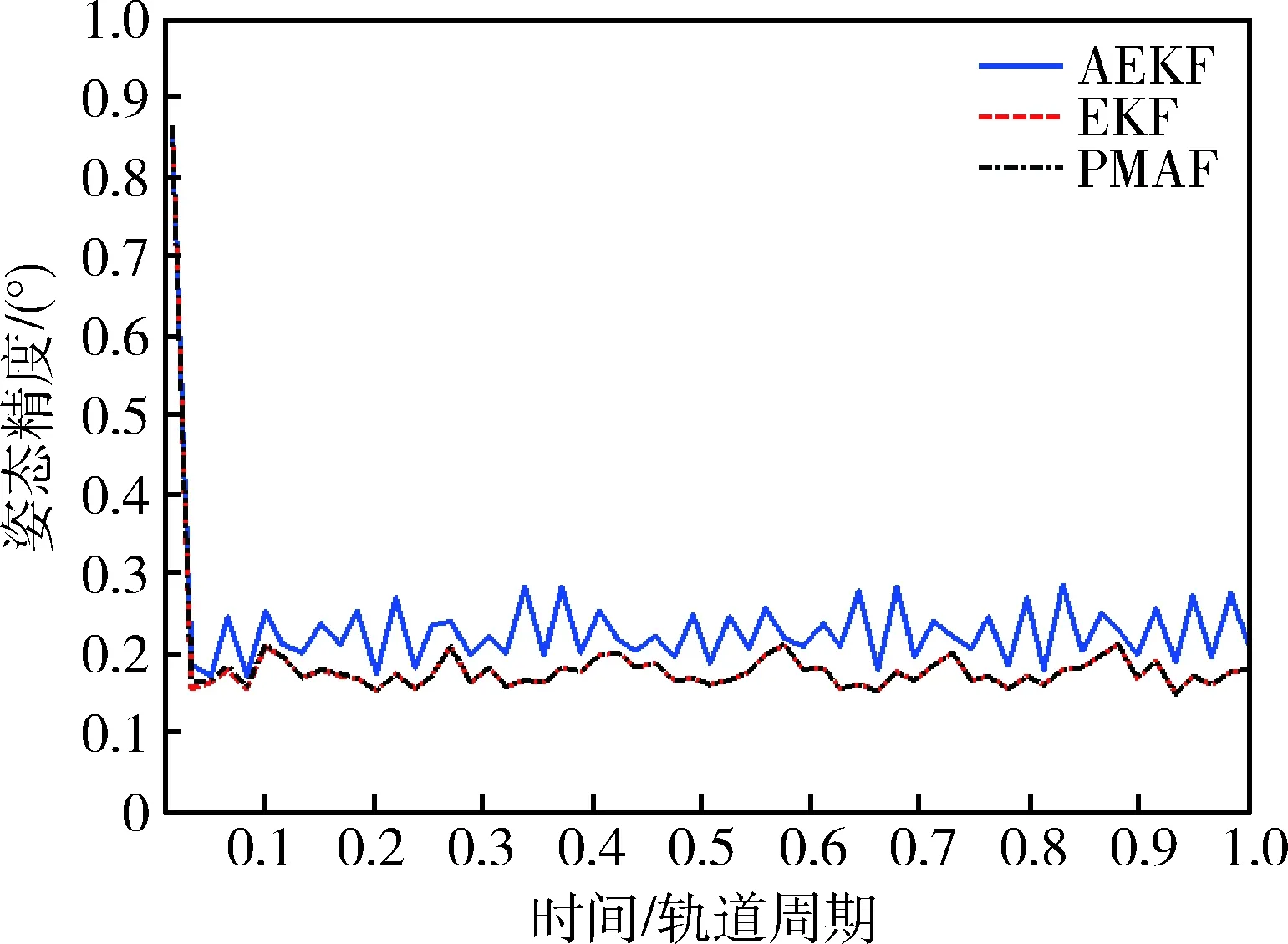
图3 相对姿态估计误差(Case 1)Fig.3 Relative attitude estimation errors in normal case

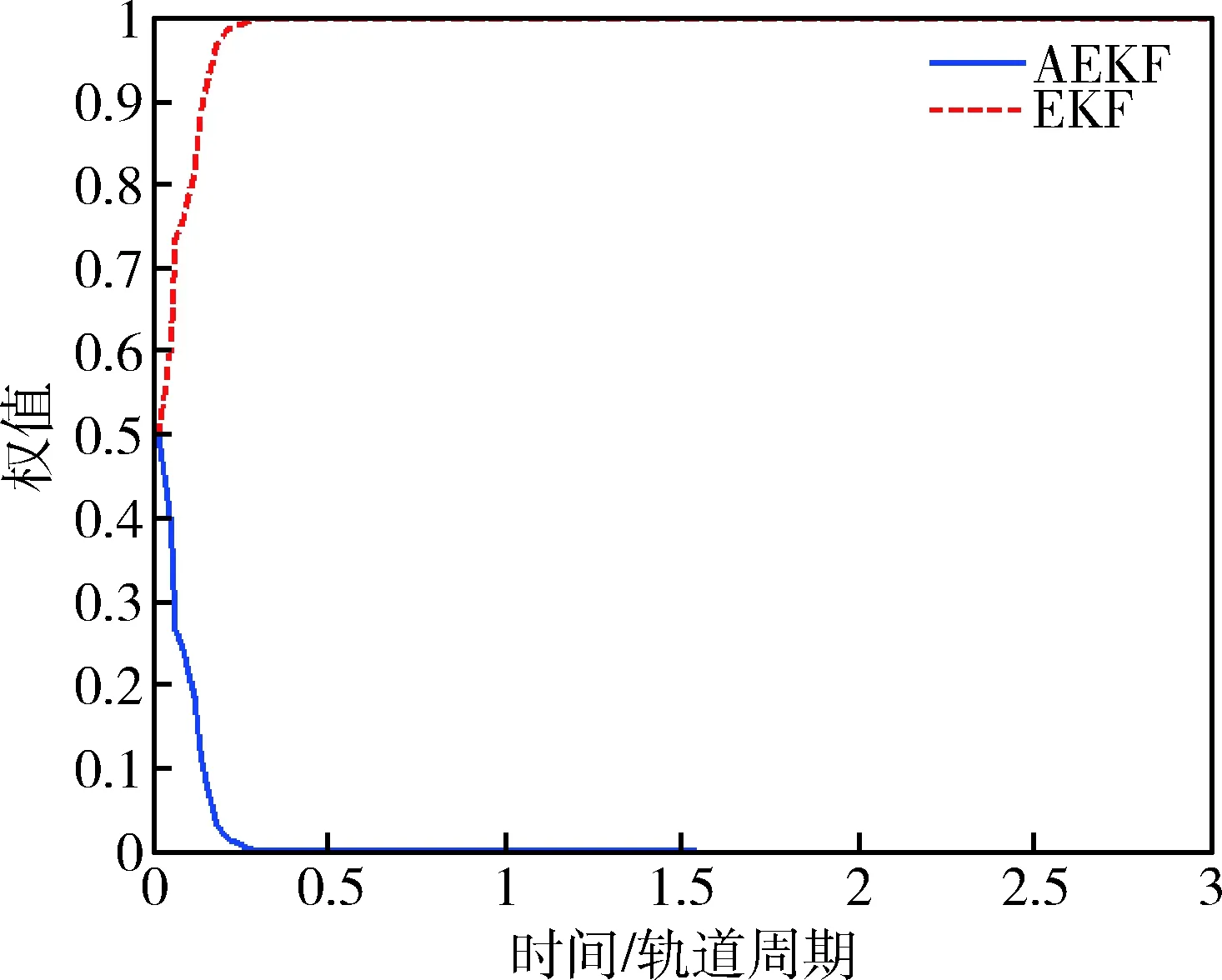
图4 并行滤波器权值变化曲线(Case 1)Fig.4 Weights for two parallel filters in normal case

Case2：测量噪声方差的真值不等于标称值

在实际的测量噪声方差增大为(0.1 m)2I12×12的情况下，通过20次仿真得到三种算法的姿态估计误差，如图5所示，相应地，两个并行滤波器的权值变化曲线如图6所示.显然，存在模型不确定性的情况下，PMAF的性能优于EKF，原因在于PMAF中的第2个并行滤波器具备在线估计测量噪声方差的能力.基于AEKF设计的并行滤波器权值收敛于1，表明所提算法可以自适应地选取适当算法进行处理.

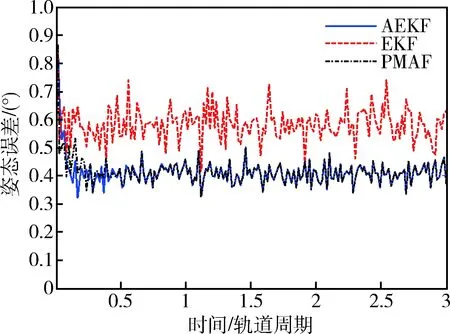
图5 相对姿态估计误差(Case 2)Fig.5 Relative attitude estimation errors indisturbance case

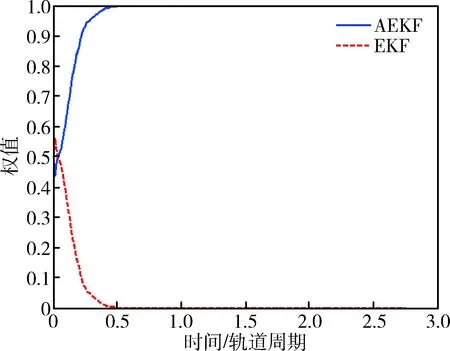
图6 并行滤波器权值变化曲线(Case 2)Fig.6 Weights for two parallel filters in disturbance case

4 结 论

本文针对带有噪声统计特性不确定性的非线性系统，提出一种并行模型自适应滤波方法，该方法充分利用了EKF和AEKF算法各自的性能优势，能够根据应用环境的变化选择适当的滤波算法进行加权融合和自适应处理，从而增强系统应对各种复杂场景的能力.以空间目标相对位姿确定为背景开展了仿真研究，结果表明，所提PMAF算法能够在不同仿真条件下取得优于传统EKF或AEKF的滤波性能.

新的滤波算法层出不穷，每种方法都有其特定的优势和适用范围，通过并行计算和智能融合，充分发挥先进滤波方法在对抗环境下多源信息处理方面的效能，是未来研究中需要重点关注的内容.