基于线性回归模型的颜色与物质浓度辨识应用研究

韦碧鹏，黎金清，刘剑锋，杨雪

（柳州职业技术学院，广西柳州545006）

1 问题背景

比色法是目前常用的一种检测物质浓度的方法，即把待测物质制备成溶液后滴在特定的白色试纸表面，等其充分反应以后获得一张有颜色的试纸，再把该颜色试纸与一个标准比色卡进行对比，来确定待测物质的浓度档位。由于每个人对颜色的敏感差异和观测误差，这一方法在精度上存在很大的不确定性。随着照相技术和颜色分辨率的提高，希望建立颜色读数和物质浓度的数量关系，即只要输入照片中的颜色读数就能够获得待测物质的浓度。试根据附件所提供的有关颜色读数和物质浓度数据完成下列问题：

（1）附件Data1.xls中分别给出了5种物质在不同浓度下的颜色读数，讨论从这5组数据中能否确定颜色读数和物质浓度之间的关系，并给出一些准则来评价这5组数据的优劣。

（2）对附件Data2.xls中的数据，建立颜色读数和物质浓度的数学模型，并给出模型的误差分析。

（3）探讨数据量和颜色维度对模型的影响。

具体附件请查看全国大学生数学建模竞赛官网（http：//mcm.blyun.com/），且下载2017年全国大学生数学建模竞赛C题进行查看。

2 问题分析

2.1 问题（1）的分析

结合附件1（Data1.xls），要研究5种物质在不同的浓度下颜色读取和物质浓度的关系。由于附件1中给出的5种物质在不同浓度下颜色读数的数据有一组，二组或者多组。首先对5种物质溶液下的数据进行求平均值，接着从不同物质溶液的角度出发，分别对颜色读取和物质浓度进行多元线性回归分析。对于物质浓度不能进行回归分析的数据，运用相关分析进行分析。最后，从方差和极差的两个角度出发对5组数据的优劣进行评价。

2.2 问题（2）的分析

结合附件2（Data2.xls），要研究颜色读数与物质浓度的关系，采用多元线性回归模型进行拟合，当采用多元线性回归模型中的Enter法进行拟合时，发现所得到的模型不满足显著条件。为了能够更好地研究颜色读数和物质浓度的数学模型，先对附件2中的数据进行双变量相关分析，运用Pearson相关系数，得出二氧化硫的浓度与颜色读数R，G，B，H，S的相关关系，接着采用多元线性回归模型中的逐步法进行拟合，得出附件2中二氧化硫浓度与颜色读取的关系模型。最后，考虑所得出模型的误差，引入了绝对误差和相对误差对其进行分析。

2.3 问题（3）的分析

为了探讨数据量对模型的影响，结合附件2中的数据，分别从数据量多少和颜色维度的多少两个角度进行分析，做4组数据实验。首先，考虑数据量多少对模型的影响，做如下两组实验。实验组A：删掉二氧化硫浓度为20 ppm与50 ppm的数据；实验组B：删掉二氧化硫浓度为100 ppm与150 ppm的数据。通过数学软件SPSS分别对实验组A、B的数据进行多元线性回归，然后用问题（2）所得出原模型的数据与实验组A、B所得出的数据进行比较，分析数据量多少对模型的影响；其次，考虑颜色维度的多少对模型的影响，我们从增加颜色维度和减少颜色维度方向出发，取附件Data2.xls中的数据做两个实验组。实验组C：减少颜色维度，删除掉H和S两个维度的数据；实验组D：增加颜色维度I。最后，用问题（2）所得出原模型的数据与实验组C、D所得出的数据进行比较，分析颜色维度对模型的影响。

3 模型假设

(1)假设题目所给附件1和附件2中的数据无误；

(2)假设各种物质的实验组数据都是在同样的环境下进行的。

4 模型建立与求解

4.1 问题（1）模型的建立与求解

4.1.1 组胺溶液的浓度与颜色读数的关系

在组胺溶液中，题目附件1给出了两组同一组胺物质浓度的数据，为了减少实验的误差，取两组实验数据的平均值，得出组胺溶液在不同的浓度下的R，B，H，S值，见表1。

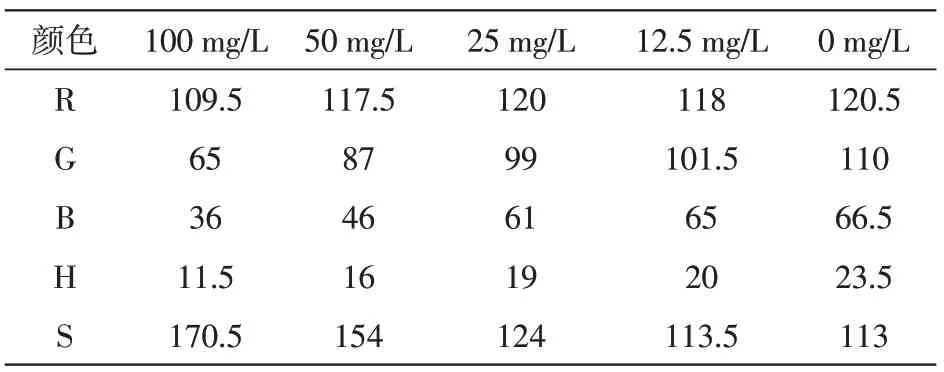
表1 两组组胺溶液的RGBHS平均值

组胺溶液中，为了研究物质浓度与颜色读数的关系，对其做多元线性回归拟合，具体模型如下：

其中y1表示组胺溶液的浓度，xR、xG、xB、xH、xS分别表示变量红色、绿色、蓝色、色调、饱和度，a1、a2、a3、a4、a5分别表示它们的系数，b表示常数。

通过数学软件SPSS22，对表1中的数据代入进行多元线性回归拟合，运用输入回归法可得结果见表2，3。

表2 变异数分析a

表3 系数a

从表2，3中可知，模型的显著性概率为0.00小于0.01，因此，该线性回归模型有效。又因为模型中常数、变量G，R，H，S的显著性概率为0.00均小于0.01，则该模型通过检验，具体模型为：

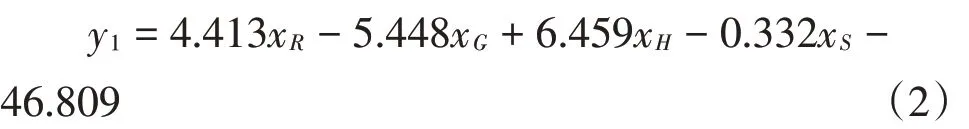
4.1.2 溴酸钾溶液的浓度与颜色读数的关系

在溴酸钾溶液中，题目附件1给出了两组同一溴酸钾物质浓度的数据，为了减少实验的误差，取两组实验数据的平均值，得出溴酸钾溶液在不同的浓度下的R，G，B，H，S值。为了研究溴酸钾溶液浓度与颜色读数的关系，同理，对其做多元线性回归拟合，通过SPSS22软件，进行多元线性中的输入回归可得结果，从中可知，模型的显著性概率为0.00小于0.01，因此，该线性回归模型有效。又因为模型中常数、变量G，R，H，S的显著性概率为0.00均小于0.01，因此该模型通过检验，具体模型为：

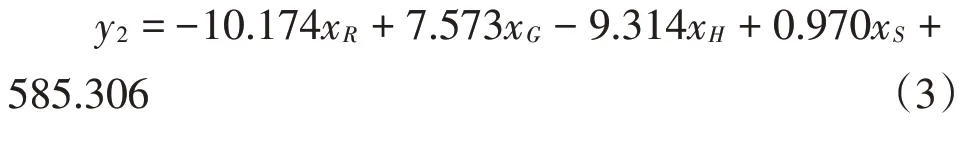
4.1.3 工业碱溶液的浓度与颜色读数的关系

在工业碱溶液中，为了研究物质浓度与颜色读数的关系，我们首先求出同一个颜色在不同浓度下的颜色读数极差，见表4。

表4 工业碱的RGBHS值

根据前面的理论，对其进行多元线性回归，发现其模型显著性都大于0.05，模型不显著。为了更好地分析物质浓度与颜色读数之间的关系，对工业碱溶液中的数据进行变量之间的相关分析，具体结果见表5。

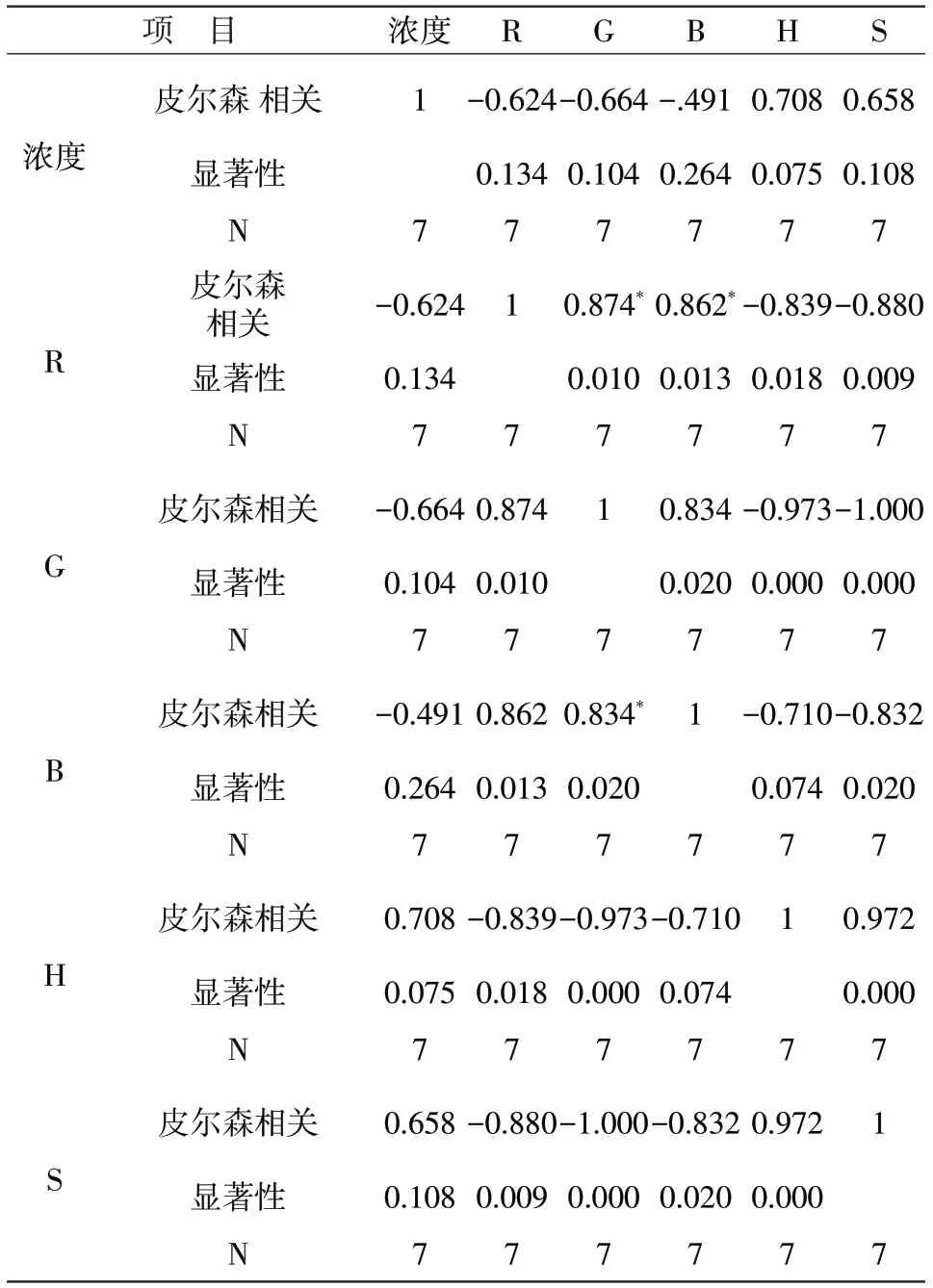
表5 工业碱溶液中的数据进行变量之间的相关分析

从表5中可以看出工业碱溶液浓度与B，G，R，H，S的相关系数都低于0.8，显著性均大于0.05，所以显著性不明显，该线性回归无效。由表5可知颜色R，G，B都随着工业碱溶液浓度的增加而减少，而色调H和饱和度S则随着工业碱溶液浓度的增加而增加，因此工业碱溶液浓度与颜色R，G，B成负相关，与H，S成正相关，从极差可以看出饱和度S对工业碱溶液浓度的影响比较大，R的影响最小。

4.1.4 硫酸铝钾溶液的浓度与颜色读数的关系

在硫酸铝钾溶液中，题目附件1给出了6组同一硫酸铝钾物质浓度的数据，为了减少实验的误差，取6组实验数据的平均值，得出硫酸铝钾溶液在不同的浓度下的R，G，B，H，S值。根据前面的做法，对数据进行多元线性回归拟合，结果发现模型的显著性不高。为了研究硫酸铝钾溶液的浓度与颜色读数的关系，对数据进行双变量分析，通过SPSS22软件计算，得出结果见表6。

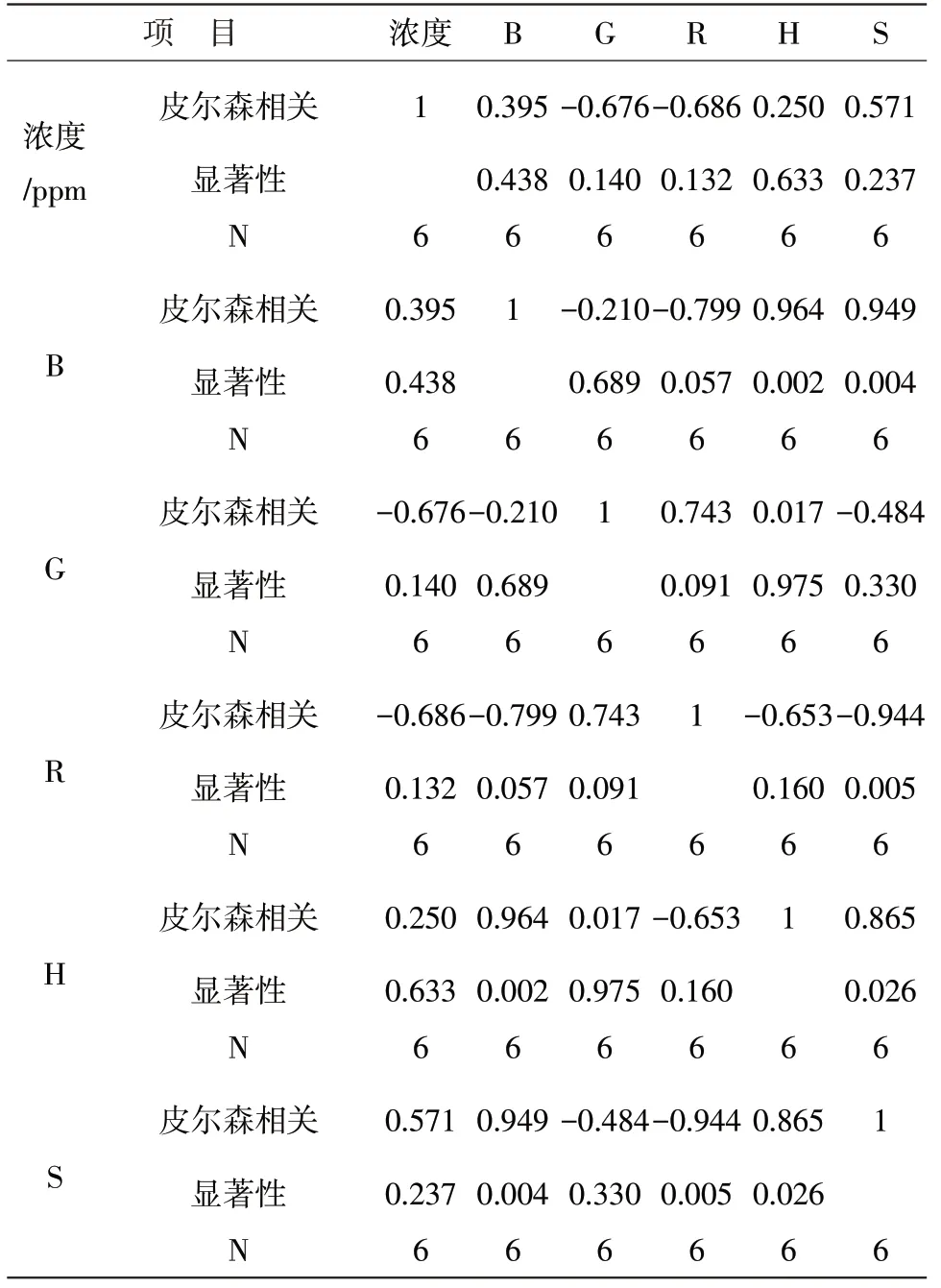
表6 硫酸铝钾溶液的浓度与颜色读数的关系

由表6可以看出硫酸铝钾溶液浓度与B，G，R，H，S的相关系数都低于0.7，显著性均大于0.05，线性回归无效，通过分析表6可以得出R随着硫酸铝钾溶液浓度的增大而减少成负相关，G随着硫酸铝钾溶液浓度的变化值不明显，成不相关，颜色B，H，S随着硫酸铝钾溶液的增大而增大，成正相关，其中S与硫酸铝钾溶液浓度的极差最大，即影响最大。

4.1.5 奶中尿素溶液的浓度与颜色读数的关系

在奶中尿素溶液中，题目附件1给出了两组同一奶中尿素物质浓度的数据，为了减少实验的误差，取两组实验数据的平均值，得出奶中尿素溶液在不同的浓度下的R，G，B，H，S值。同理，对其进行多项式拟合，通过数学软件SPSS可以得出结果，该模型的显著性为0.027小于0.05，回归系数B，R，H，S的显著性均小于0.05，所以线性回归方程有效，B，R，H，S的线性回归方程为：

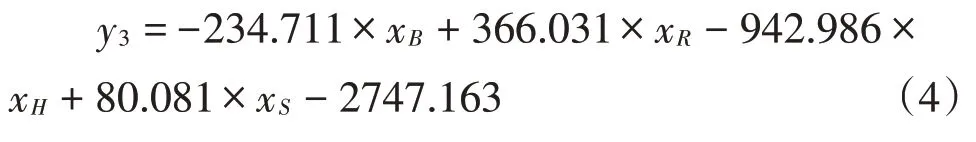
4.1.6 评价5组数据优劣性的模型

（1）从方差角度判别数据的优劣。要判别5种物质数据的优劣，采用整理取平均值后的数据进行分析，用Excel软件求取各组物质浓度与颜色读数关系的方差，从而求出各种物质浓度的方差平均值见表7。

表7 各种物质浓度方差

根据统计学知识，数据方差的值越小，即数据越稳定。因此，这5组数据从优到劣的顺序依次为：组胺＞奶中尿素＞溴酸钾＞硫酸铝钾＞工业碱。

（2）从极差角度判断数据的优劣性。同上所示，采用整理取平均值后的数据进行分析，用Excel软件求各组物质的浓度与颜色读数关系的极差，从而求出各种物质浓度的极差平均值，见表8：

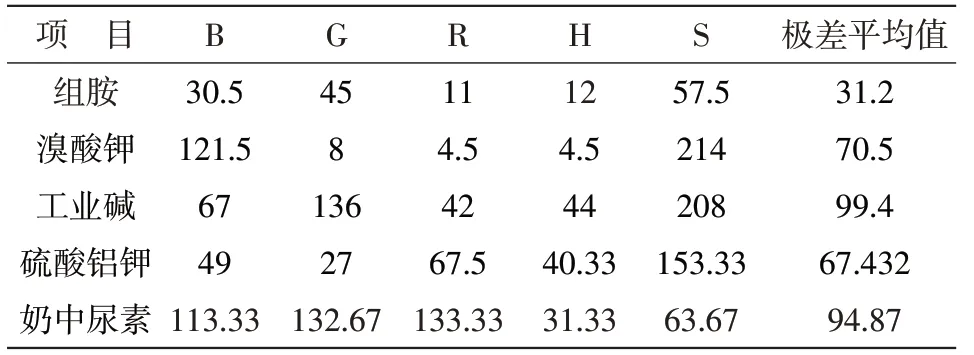
表8 各种物质浓度的极差

研究不同物质溶液对不同颜色读数数据的优劣性，根据极差越小，证明数据越稳定原则。这5组数据从优到劣的顺序依次为：组胺＞硫酸铝钾＞溴酸钾＞奶中尿素＞工业碱。

4.2 问题（2）模型的建立与求解

4.2.1 建立颜色读数和物质浓度的数学模型

首先对附录2中的数据进行补充完整，要研究颜色读数与物质浓度之间的关系，根据问题（1）的思路，建立多元线性回归模型。运用SPSS软件对其数据进行拟合，拟合方法选取Enter法，得出如下结果（见表9，10）。

表9 变异数分析a

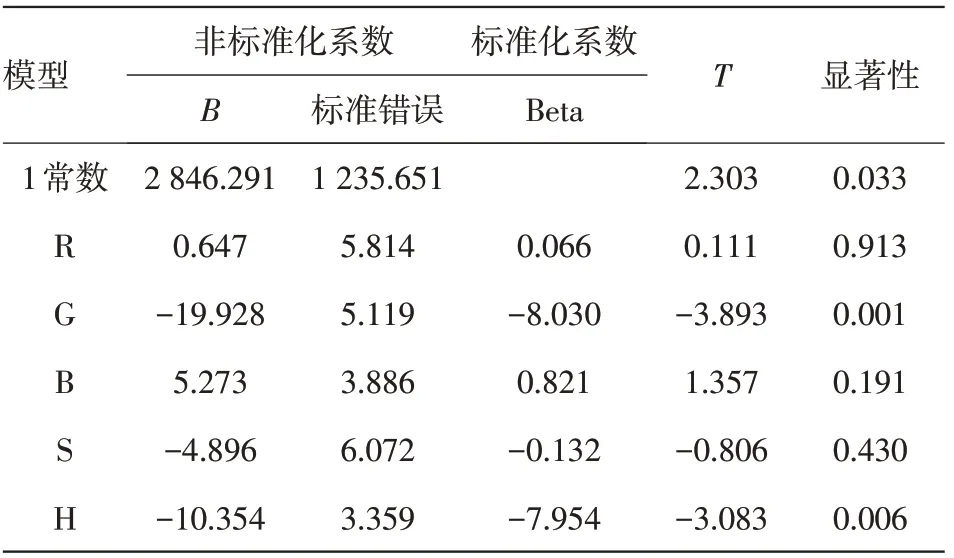
表10 系数a

根据以上结果，虽然该模型的显著性小于0.01，然而，可以看出模型中颜色变量G，B，S的显著性大于0.05。因此，运用多元线性回归模型Enter输入法进行拟合的线性回归模型失效，因此该模型不好。为了能够更好地研究颜色读数和物质浓度的数学模型，我们先对附件2中的数据进行双变量相关分析，运用Pearson相关系数，得出相应的结果。从结果中可以看出，二氧化硫的浓度与R，G，H的相关系数较高，从而可判断，二氧化硫的浓度与R，G，H有关。接着，通过SPSS22软件进行多元线性中的逐步回归得出结果，见表11，12。

表11 模型摘要

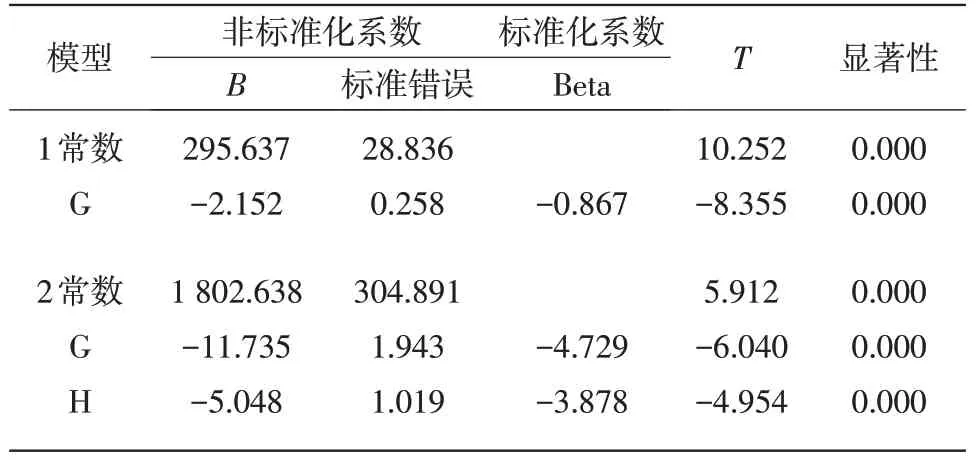
表12 系数a

可以得出，在显著性相同的情况下，模型2的R值比模型1的R值大，因此选择模型2更为合理。由此可得数学模型：

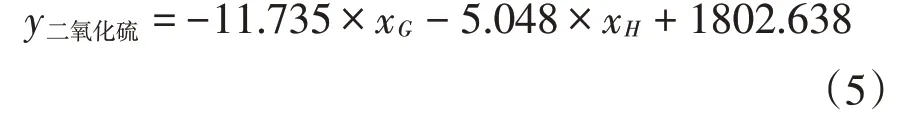
其中y二氧化硫表示的是二氧化硫的浓度，xG表示颜色绿色的读数，xH表示色调的读数。

4.2.2 模型的误差分析

为了考虑所得出模型的误差，我们引入了绝对误差和相对误差对其进行分析，具体公式如下：绝对误差公式为：

其中：L为绝对误差，N为真实值，M为预测值。

相对误差的公式为：

结合附件2-1中的数据，在模型（5）的作用下，我们得出模型（5）的预测值，接着，运用公式（6）和公式（7），得到表13：

从表13可以看出该模型数据的相对误差0～1.8的范围内，产生如此大的误差，可能是由于数据的不稳定造成的。

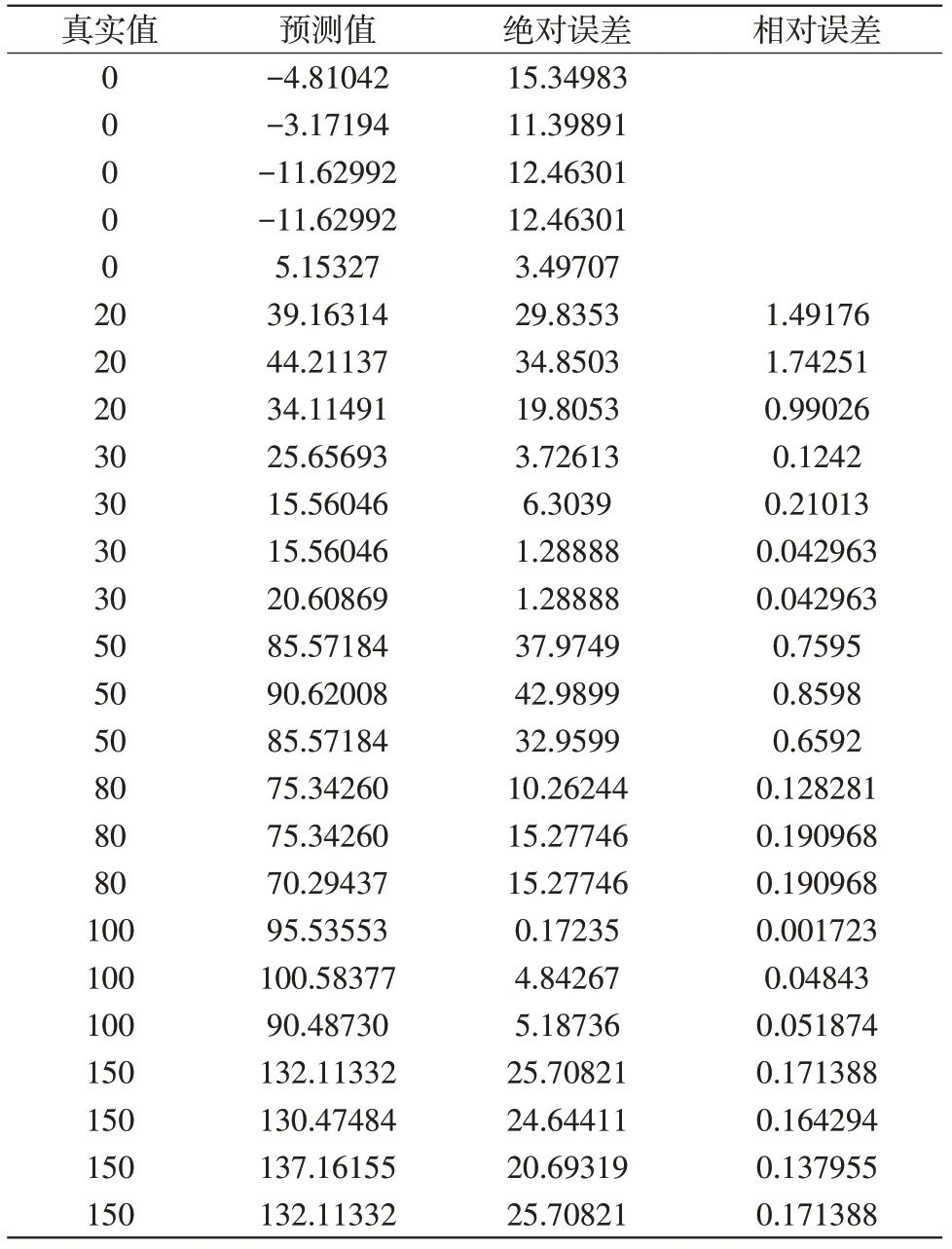
表13 预测、绝对误差与相对误差的值

4.3 问题（3）模型的建立与求解

4.3.1 数据量对模型的影响

为了探讨数据量对模型的影响，取附件2中的数据，做两组实验，实验组A：删掉二氧化硫浓度为20ppm与50ppm的数据。实验组B：删掉二氧化硫浓度为100ppm与150ppm的数据。通过数学软件SPSS对实验组A中的数据进行多元线性回归拟合，运用逐步法可得结果，见表14，15。

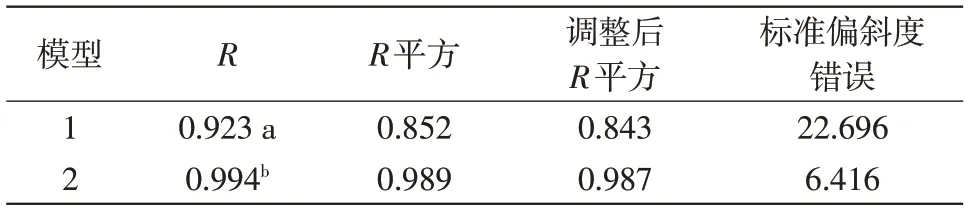
表14 模型摘要

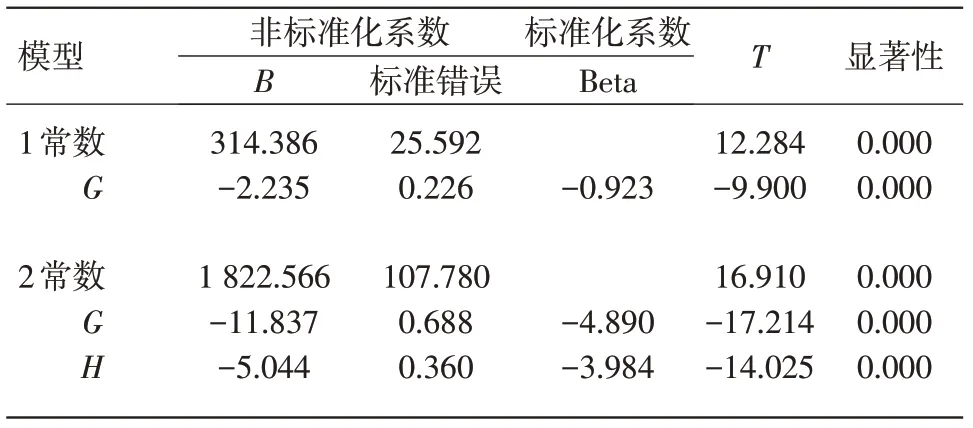
表15 系数a

从问题（2）的模型，可以知道在二氧化硫浓度下，未删减数据时模型的R值为0.940，显著性均为0。然而，实验A模型的显著性也为0。因此，删除数据的实验A与未删除数据中问题二模型的显著性是相同的。但是，通过做回归发现，实验组A中的R相比原数据的R值大，可以看出数据量对模型是有影响的。为了能够减少实验中一些非主要因素的干扰，我们在做一组实验进行分析。同理，运用实验组B中的数据进行多元线性回归拟合，得出结果，见表16，17。

表16 模型摘要b

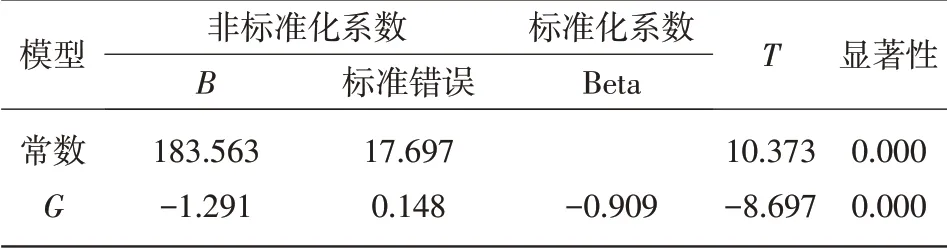
表17 系数a

在模型显著性一样的前提条件下，可以看到实验组B模型的R值小于原数据模型的R值。因此，从两组实验组综合起来比较，可能实验B中删除时删掉了在浓度中主要的数据这种情况。通过用原数据与实验组数据之间预测值差距，进一步判断数据量对模型的影响，见表18。

表18 原数据与实验组数据预测值比较

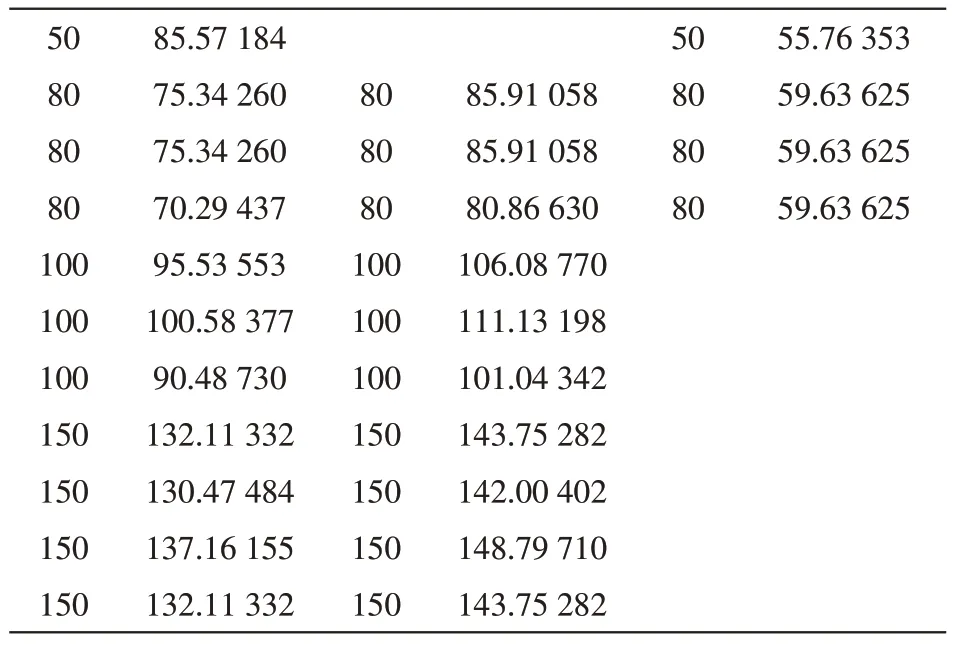
50 80 80 80 100 100 100 150 150 150 150 85.57 184 75.34 260 75.34 260 70.29 437 95.53 553 100.58 377 90.48 730 132.11 332 130.47 484 137.16 155 132.11 332 80 80 80 100 100 100 150 150 150 150 85.91 058 85.91 058 80.86 630 106.08 770 111.13 198 101.04 342 143.75 282 142.00 402 148.79 710 143.75 282 50 80 80 80 55.76 353 59.63 625 59.63 625 59.63 625

从表18中，可以明确地看出，未删减过的数据与删减过的数据对模型有着很明显的影响，因此，可以得出数据量的多少与模型是有显著影响的。

4.3.2 颜色维度对模型的影响

为了更好探讨颜色维度对模型的影响，我们从增加颜色维度和减少颜色维度的两个方向出发，同样，取Data2.xls中处理过的数据做两组实验。

根据参考文献[3]可知，颜色维度I等于颜色维度R、G、B三者的平均值。

实验组C：减少颜色维度，删除掉H与S中的数据；实验组D：增加颜色维度I的数据。通过数学软件SPSS对实验组C中的数据进行多元线性回归拟合，运用逐步法可得结果，见表19，20。

表19 模型摘要

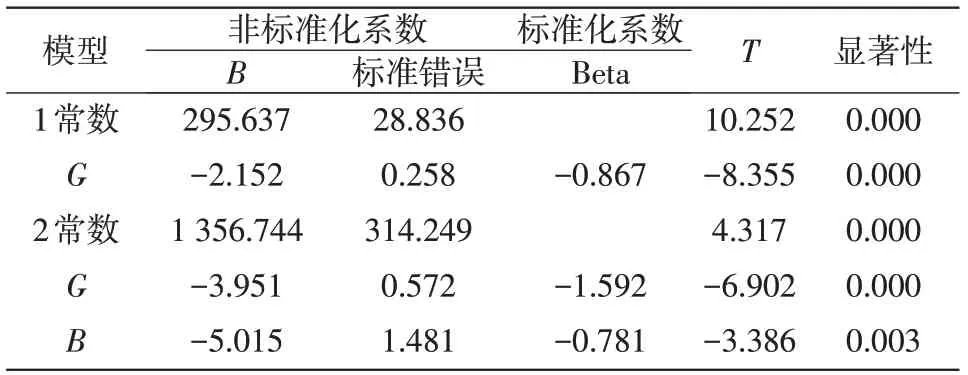
表20 系数a

从问题（2）的模型，可以知道在二氧化硫浓度下，原来模型的R值为0.940，显著性均为0。然而，实验C模型的显著性也为0。因此，删除维度的实验C与问题二模型的显著性是相同的。同时，我们通过做回归发现，实验组C中的R相比原模型的R值相差不大。为了能够更好地分析颜色维度对模型的影响，同理，继续做实验组D中的数据进行多元线性回归拟合，得出结果。在模型显著性一样的前提条件下，实验D模型的R与原模型相差也不大。因此，我们继续通过原模型数据与实验组数据之间的预测值进行比较，见表21。

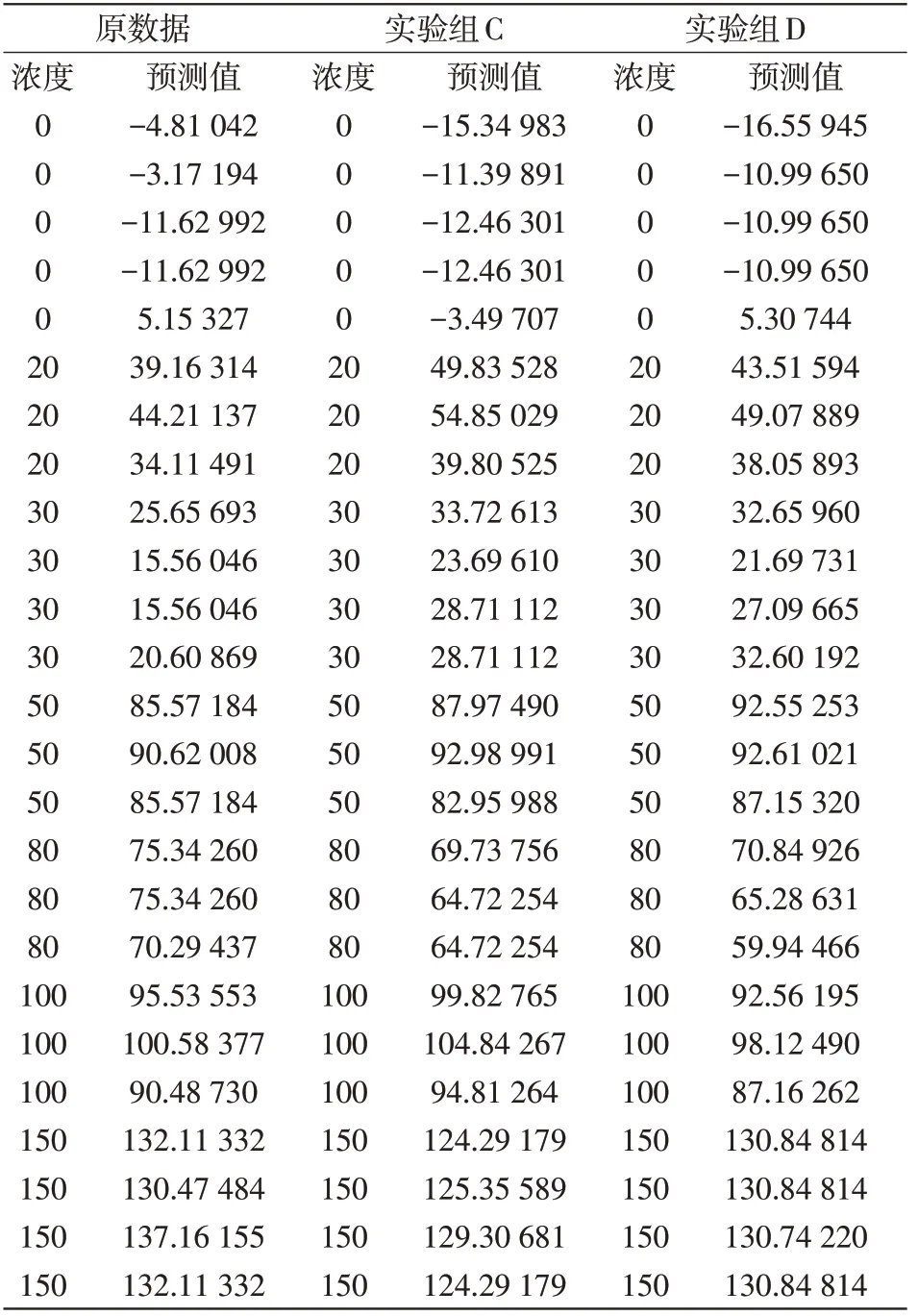
表21 原数据与实验组数据预测值比较

由表21可知，颜色维度的增减对于模型的影响还是较为明显的。

5 结语

为了研究颜色读数和物质浓度之间的关系，本文结合2017年全国大学生数学建模竞赛C题目，详细地对不同物质颜色读数和浓度之间的关系进行研究，且通过4组实验探索数据量增加与减少、颜色维度增加与减少对模型的影响。其次，本文考虑问题能够从多个角度对问题进行分析，给出分析结果，准确性高；通过数学软件Excel、SPSS对数据进行分析和处理，操作简便，适用性强；且该模型具有较大的普遍性，便于应用到类似的实际问题中，如：解决有关医学研究、药物测量与制作及化学等领域。