5轴数控机床空间误差模型及辨识方法研究*

左 维，李 巍

(天津中德应用技术大学 机械工程学院，天津 300350)

0 引言

5轴数控机床加工零部件范围广，加工形式灵活，可加工叶轮、曲轴等包含复杂曲面的零件。由于CAD/CAM在设计制造中应用普及性增强，5轴机床的应用也越来越广泛，5轴数控机床的运动精度问题就显得尤为重要。随着对数控机床的运动精度研究不断深入，尤其是3轴机床21项误差及5轴机床37项独立误差的确定[1]，对数控机床的误差研究从基于统计学转变为基于数值方法[2-3]。在加工曲面或曲线过程中，误差的耦合是大量存在的。许多学者对单根进给轴的误差进行了解耦分析，并取得了一定成果[4-5]。而正确、高效的误差辨识技术正是误差解耦补偿的前提[6]。

球杆仪作为一种快速误差检测仪器，具有高效率、高精度的特点。在工业中有着广泛应用，但球杆仪的算法及误差模型并不开放，进行误差辨识研究有一定的难度，许多学者采用球杆仪进行过误差辨识方面的研究[7-8]。其中，梁莹莹等提出了改变球杆仪杆长及测量高度的方法进行误差辨识，可有效检测出同一坐标系下全部6个误差元素[9]，该方法具有高精度、易进行数值等优点。

近来，有学者提出球杆仪安装尺寸对检测过程的影响不容忽略[10]。为了避免频繁调整球杆仪安装尺寸对最终检测结果的影响，本文以自主设计的五轴数控机床和国产开放式数控系统作为研究对象，建立了五轴机床空间误差模型。并在该模型基础上，组合使用球杆仪和激光干涉仪，针对工件坐标系及刀具坐标系间的联动插补开展辨识研究。

1 机床综合误差建模及辨识原理

1.1 机床综合误差模型

本文研究对象为一台5轴数控机床，其机械结构为摆头——回转台式，由三根直线轴X、Y、Z，两根旋转轴A、C组成。其中A轴为机床摆头，围绕X轴旋转；C轴为机床回转工作台，围绕Z轴旋转，机床进给轴运动范围为1200mm×950mm×1100mm，如图1所示。拓扑结构为树形结构，有两条运动支链，如图2所示。

根据多体理论进行机床坐标系建模，MCS为机床坐标系，与地面固定。TCS和WCS为刀具坐标系与工件坐标系，将球杆仪固定在TCS与WCS中，则二者分别是运动的两个末端。XCS、YCS、ZCS为轴的进给轴坐标系，ACS、CCS为带动刀具坐标、工件坐标系旋转的两个旋转轴坐标系。球杆仪在图中标记为DDB，直接工作在机床摆头与回转工作台所两个坐标系之间，反映由MCS—>YCS—>ZCS—>ACS—>TCS和MCS—>XCS—>CCS—>WCS两条运动支链形成的综合误差：

(1)

式(1)中即为单摆头——回转台五轴系统综合误差，球杆仪测量的机床空间误差反映了机床两条运动支链分别累计的误差，即机床综合空间误差。

图1 5轴机床机械结构及各轴定义

图2 5轴机床拓扑图

1.2 球杆仪误差辨识原理

已有的球杆仪辨识方法，大体是通过改变球杆仪杆长及改变球杆仪安装位置的方式，一次辨识出同一坐标系内6个误差元素。这种辨识方式，将误差认定为发生在一组坐标系内，忽略了多体拓扑结构中坐标系之间的误差，因此多适用于三轴机床的误差分析；且安装位置的精确度要求极高，尤其是拆装过程重复定位精度效果较差，否则会影响辨识准确性。

对于5轴空间插补复杂的机床误差，因其空间坐标系间联动决定曲面成型质量，需要考虑如前述坐标系之间的相对误差，传统辨识方法则不适用。通过本文中的方式可以有效避免球杆仪的二次装配，提高辨识准确性；采集空间内不同平面的特征点进行分析运算的方法，大大降低了计算难度，对于提升辨识效率有较大提升。将球杆仪一端安装在工作台上，其理论中心位置用O1表达，在坐标系中位置为(x1,y1,z1)；另一端安装在主轴上，理论中心位置用O2表达，在坐标系中位置为(x2,y2,z2)。根据空间勾股定理可得到球杆仪的长度与坐标位置关系：

(2)

(3)

用式(3)减去式(2)，可以得到：

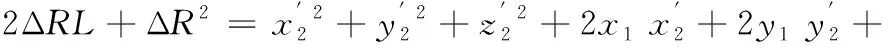
(4)

将上式化简，可得关于球杆仪半径变化与各进给轴误差分量的关系：

(5)

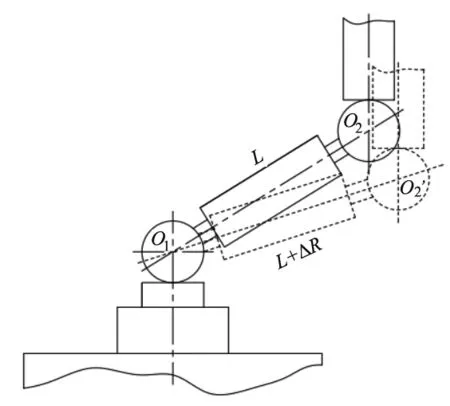
图3 球杆仪工作状态

2 空间误差测量模型

一个旋转轴在运动过程中会产生6个自由度的误差，以O1为原点建立坐标系，设球杆仪浮动端中心O2在WCS下齐次坐标为P。对其齐次坐标变换进行推导，若将O1在Z方向位置与回转台工作中心Z轴重合，设球杆仪沿杆方向与X轴夹角为θ，杆长为一固定数值L。其工作状态如图2所示，通过X轴与Y轴进行圆弧插补工作，此时两个旋转轴及垂直位移轴为静止状态，ACS、CCS、ZCS矩阵的误差传递矩阵退化为单位矩阵。浮动端中心O2理想初始齐次坐标可描述为Pi=[cosθL,0,sinθL+h,1]T，X、Y轴进行圆弧插补工作时，设在X-Y平面内旋转角度为α，此时θ为一常数，则一般状态下的齐次坐标可以表示为:

Pi=[cosαcosθL,sinαL,sinθL+h,1]T

忽略二阶项，可将上式修正为式(6)：

(6)

O2′在考虑误差影响情况下的实际坐标Pa：

(7)

式(7)已知量θ、L、h，未知量εxx′、εyx′、εxy′、εyy′、εxz′、εyz′、δxx′、δxy′、δxz′。其中，δxx′、δxy′、δxz′为X轴运动对三个进给轴产生的位置误差，即直线度误差。Pa与Pi之差即为球杆仪长度变化，从齐次坐标矩阵中提取X、Y、Z三个方向上的分量即为Δx、Δy、Δz，代入式(5)可得出ΔR关于各误差分量的方程：

ΔR={[cosαcosθL+sinαL(-εxz′+εyz′)+(εxy′-εyy′)
(sinθL+h)+δxx′](x2-x1)+[cosαcosθL(εyz′+εxz′)+
sinαL+(sinθL+h)(-εxx′+εyx′)+δxy′](y2-y1)+
[ cosαcosθL(εxy′-εyy′)+sinαL(-εyx′+εxx′)+
sinθL+h+δxz′](z2-z1)} /L

(8)

由式(8)可知，9个未知量需要9组不同方程组才能解出，为了简化计算过程，其中三个直线度误差δxx′、δxy′、δxz′可视为静态误差，先行通过激光干涉仪进行消除。简化后可通过6个独立方程对式(8)进行误差辨识并将误差因素进行分离，如式(9)所示。该方程式表达球坐标下TCS坐标系相对于WCS坐标系6个旋转误差分量的产生导致球杆仪长度变化这一现象。

ΔR′={[cosαcosθL+sinαL(-εxz′+εyz′)+(εxy′-εyy′)
(sinθL+h)](x2-x1)+[cosαcosθL(εyz′+εxz′)+sinαL+
(sinθL+h)(-εxx′+εyx′)](y2-y1)+[ cosαcosθL(εxy′-
εyy′)+sinαL(-εyx′+εxx′)+sinθL+h](z2-z1)} /L

(9)

3 五轴空间误差测量实验

3.1 实验方法与数据

使用激光干涉仪对直线度误差进行辨识与补偿，待通过螺距补偿方法消除了三个方向直线度误差对机床坐标系的影响后，将雷尼绍QC20-W球杆仪安装在五轴机床上，见图4。对机床参与XOY平面插补的两个坐标系XCS及YCS进行总计12个角度误差因素进行辨识。在实验中，选用球杆仪测量条件为：L=100mm，h=100mm，并在θ=0°,15°,30°,45°,60°,75° 6种角度进行插补工作。由于插补实验采集信息量较大不利于后期分析，采用选取其特征点的工作方式进行简化，将每个工作圆面间隔60°进行取值。由于在工作过程中伴随着热误差存在，且其与机床几何误差耦合，为了使测量结果为稳态误差结果，机床测试前进行了6h热机，测试时严格保证外界环境温度条件为20°C，分为顺时针与逆时针两次进行。

(a)θ=0°球杆仪实验工作状态图 (b)θ=60°球杆仪实验工作状态 图4 球杆仪实验时工作状态

3.2 实验结果处理与分析

将实验数据代入式(9)中，可以得知矩阵满秩，此时有特定解。利用高斯消元法可计算出6个方向分量计算结果分别为：

εxx′=0.0006、εyx′=0.0007、εxy′=0.0009、
εyy′=0.0009、εxz′=0.0003、εyz′=-0.0006。

将部分空间角度对应的数据进行整理，可以得出在指定角度平面中的旋转误差元素。由表1中数据可见，由不同θ组成的空间平面内误差元素是有变化的，且其变化成线性关系，其数值变化在空间圆平面内呈连续变化状态，这是由于球杆仪在测量时的轨迹遵循空间圆平面而产生的。按照如上方法，在XOY平面上进行了旋向为逆时针的空间圆弧轨迹测试，并得出部分旋转误差元素大小如表2所示，其在相同特征点位置上的数值大小基本相同。即在进行静态补偿的基础上，数控机床做顺时针运动与逆时针运动，其旋转误差的大小基本相同。

表1 XOY平面顺时针旋转角度误差

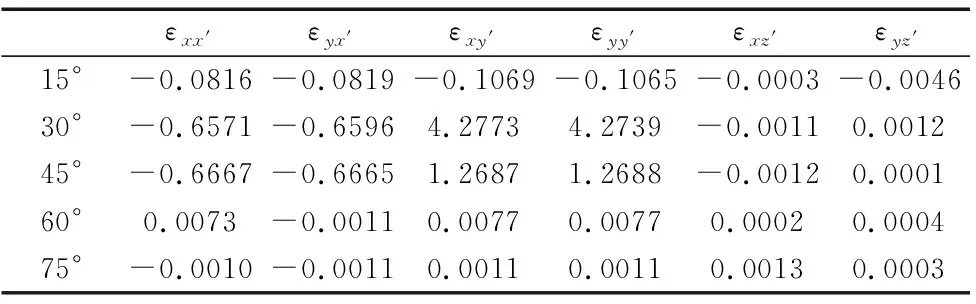
表2 XOY平面逆时针旋转角度误差

由两表中数值对比分析，可以得出：

(1)在同一空间中，不同轨迹形成的旋转误差元素并不相同。

(2)同一运动轨迹所形成的平面中，旋转误差元素呈连续变化规律。

(3)误差变化趋势基本满足运动圆弧直径越大误差越大的规律。

(4)将静态误差中的直线度误差消除后，仍将产生坐标系间旋转误差。

(5)坐标系间产生的旋转误差，其误差量大小基本与轨迹旋转旋向无关。

4 小结

通过误差建模与实验，本文提出了一种基于球杆仪测量5轴机床工作误差的方法，通过采集空间不同平面特征点的方式，快速计算出机床空间误差。通过该方法可以有效辨识出TCS与WCS两个坐标系下6项不同回转误差元素的具体数值。联合激光干涉仪，则可以辨识出加工误差中全部12项误差元素。以5轴数控机床作为实验载体，验证了空间中不同圆形轨迹产生的旋转误差并非常量这一机床误差特性。在此基础上揭示了不同角度对应误差元素数值的规律。实验结果精度等级，超过数控机床加工精度要求一个数量级，可满足加工及补偿要求。可以此辨识方法为依据，进行误差运动解耦分析及误差补偿等工作，也为5轴数控机床进行后续插补轨迹优化及误差对曲面精加工的影响等研究打下基础。