基于电路计算的理性安全多方求和协议*

张恩,朱君哲,范海菊,李功丽

1.河南师范大学 计算机与信息工程学院,新乡 453007

2.智慧商务与物联网技术河南省工程实验室,新乡 453007

1 引言

安全求和协议作为安全多方计算的一种实例,在分布式环境下的隐私保护、电子选举、社会网络分析中有着广泛应用.安全求和协议是指有n个参与者,其中Pi输入为si,i=1,···,n,经过运算,最后每个参与者得到s=si.当协议结束时,如果参与者仅知道自己的输入和输出,那么称协议是安全的.目前已经有一系列文献[1-9]对安全求和协议进行了研究.文献[1–3]均采用的方法是,假设s=∑的范围在[0,···,l]中,P1从[0,···,l]中随机选择一个数R,将(R+s1)modn发送给P2,因为R是随机选择的,所以(R+s1)modn是均匀分布的.P2不会了解s1的值,然后P2加上自己的值发给P3,依此类推,即Pi收到S=R+sj,i=2,···,n,Pn将最后的结果发给P1,P1减去R得到最终的求和值,然后告诉其他人,在这个过程中,没有参与者能够了解自己输入和输出之外的信息.但是该方案不能抵抗合谋,因为Pi-1和Pi+1能够通过比较他们发送和接收的值算出Pi的输入si.Shepard等[4]提出一种分割圈安全求和算法(CPSS),在他们的算法中,有C个不同的汉密尔顿圈,P1首先将s1和R相加,然后分成C个不同的随机数沿着不同的汉密尔顿圈发送.最终P1收到不同汉密尔顿圈发来的值后,将随机数消去得到结果.Mehnaz等[5]提出了一种基于诚实模型的安全求和协议,并且应用到了机器学习中.Liu等[6]提出了一种基于双粒子Bell态的量子安全多方求和协议.Jung等[7]提出了一种没有安全通信信道或没有可信密钥分发者的安全求和协议,该协议可抵抗K个敌手的攻击后将字符串模式匹配问题转化成集合成员判定问题,Ashouri-Talouki等[8]提出了无需安全信道的3个安全求和协议.

但是,以上所有的方案都有一个共同的缺陷,当参与方第一个了解求和的值之后,其没有动机将结果发给其他人,即协议的公平性无法保证.虽然有一系列协议[9-13]对安全计算中的公平性进行了研究,但都限于两方参与者.田有亮等[14]提出一种通用可组合安全的公平多方计算协议.文献[15–17]分别对理性安全多方计算进行了研究.Zhang等[15]提出基于声誉系统的服务器辅助的隐私集合交集协议,该协议允许参与各方使用不同的对称密钥,最终所有的用户都可公平的得到计算结果，但该协议只适用于隐私集合比较.Kargupta等[16]基于博弈论提出一种理性安全求和协议,诚实者通过将计算量加大等措施,对发出合谋邀请的参与者惩罚,使其在协议执行时没有合谋的动机,但在他们的协议中,参与者可以在协议执行之后合谋攻击,从而获得诚实者的隐私输入.王伊蕾等[17]介绍了理性安全多方计算的发展状况及典型成果,并提出一些需要进一步研究的问题.

针对以上问题,本文结合密码学与博弈论,构建了一种基于电路计算的理性安全多方求和协议.电路计算是设计安全多方计算协议的关键,在密码学中起到了举足轻重的作用.本文主要工作如下:(1)结合密码算法和博弈论对参与者的策略和效用进行了分析和设计,构建了电路计算的概率效用模型;(2)参与者遵守协议的收益比背离协议的收益大,所以参与者有动机遵守电路计算的每一步;(3)不需要拥有大多数诚实参与者这个强条件,该协议也能够保证每个成员在点对点通信网络环境下公平地获得求和结果并且能够抵抗至多n-2个成员的合谋攻击.

2 定义与模型

2.1 基础定义

定义1安全多方求和.在交互概率图灵机集合(M1,···,Mn)中,每一个图灵机有公开输入带、私有输入带、私有随机带、隐私输出带和公开输出带,令1k为安全参数,xi为Pi的输入,Di为xi选择的域,令f:D1×D2×···×Dn→S,是一个单输出的多方求和函数.

定义2安全计算.令sum是一个求和功能,π是可以计算sum的多方求和协议,=(x1,···,xn),辅助输入为z,如果对每个概率多项式算法A(代表真实模型下的敌手策略),存在一个概率多项式算法B(代表理想模型下的敌手策略)满足

其中REALπ,A(z)()表示协议π在真实模型下的联合执行,IDEALf,B(z)()表示f在理性模型下的联合执行.则称协议π安全计算sum.

定义3多方输入承诺功能[18].

其中,r在{0,1}|x|2上均匀分布.

定义4多方扩展投币[18].对任意多项式l:N→N和多项式时间可计算功能g,多方扩展投币的定义为:

其中,r在{0,1}l(n)上均匀分布.

定义5多方认证计算[18].令f:{0,1}∗×{0,1}∗→{0,1}∗,h:{0,1}∗→{0,1}∗是多项式时间可计算的.h-认证f-计算的m-方功能定义为:

如果βi=h(α)则否则

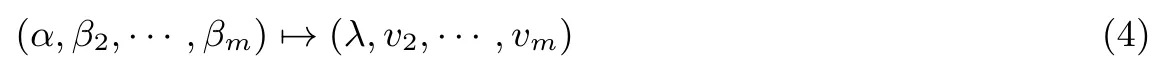
定义6纳什均衡.在博弈中,策略组合a=(a1,···,an)∈A是一个纳什均衡,如果任一博弈方i的策略都是对其余博弈方策略的最佳对策,也就是说博弈保持

因为纳什均衡具有一致预测的特性,每个博弈方都可以预测某个结果,也可以预测对手会预测它,还可以预测对手会预测自己会预测它······,通过预测来了解每个博弈方的策略及博弈的结果.

2.2 电路计算模型

电路计算在密码学中有着非常重要的作用,是安全多方计算协议的关键环节,一个算法电路是一个有向非循环图,每个逻辑门相当于一个节点,其有输入和输出边,称作逻辑门的输入线和输出线,首先每个参与者将自己拥有的电路的输入线分成n个子份额,通过电路计算,每个参与者得到每个电路输出线的子份额,然后每个参与者将子份额发给其他参与者,这样可以得到电路计算结果.而逻辑门是一种电子装置,它有一个或者两个输入,只有一个输出.常用的有与门、非门、或门和异或门等,利用与门、或门、非门三种基本的逻辑门电路可组成复杂的复合门电路,且任何逻辑电路都可以由与门和异或门组合实现.

例如:图1为半加器结构图.为了完成两个一位二进制数相加,在不考虑相邻低位的进位的情况下,完成两个一位二进制数相加称为半加,半加功能电路图的实现称为半加器.半加器由一个与门和一个异或门组成.显然,与门具有进位功能,异或门具有半加器求和的功能.输出逻辑表达式为式(6).

以安全多方电路求和为例,假设有m个参与者,Pi(i=1,···,m)的隐私输入串为xi=0,1}n,协议在结束后,如果每个参与者都了解f(x1,···,xm)=∑,且没有人了解其他参与者的输入,那么认为此协议是安全的.下面首先构造加法电路,不能简单使用前面介绍的半加器,因为这时不仅要考虑两个本位数相加,还要考虑将低位向本位的进位一起相加的运算,而实现全加功能的电路叫全加器.为了描述方便,以两方为例,如果用Ai,Bi表示第i位的两个加数,用Ci-1表示相邻低位的进位,Ci表示往相邻高位的进位,Si表示本位相加和,那么构造的一位加法器如图2所示.

图2 1位全加器Figure 2 One bit full adder

输出逻辑表达式为:

多位的加法器可以采用将一位加法器串行或者并行的方法实现,这里不再赘述.

假设每个参与者拥有逻辑求和电路每条输入线值的子份额,等计算完成时,参与者拥有这个求和电路每一根输出线值的子份额,此外不产生任何其他的附加信息.具体如下:首先每个参与者分割自己的输入,将输入值的每一位产生m个子份额.也就是说Pi(i=1,···,m)方产生(),其中然后Pi将子份额发给相应的参与者,例如第一方将发给第二方,将发给第m方.经过电路计算后,Pi分别拥有电路输出线zi=0,1}n每一位的子份额.这样计算完成后,每一方只知道自己的输入和输出结果,其余的信息都不了解.传统的电路计算可以保证参与者输入的隐私性,但是却很难保证计算的公平性.针对这个问题,本文结合博弈论和密码算法,构建了理性电路计算模型,在所设计的模型中,理性的参与者没有合谋的动机,参与者根据自身效用得失,选择诚实地遵守协议,最终每个参与者能够公平地得到计算结果.

2.3 理性电路计算模型

在理性电路计算模型下,参与者不会像半诚实攻击者那样严格遵守协议规则,也不像恶意攻击者那样任意偏离协议,而是每个参与者都是理性的,所有策略都是为了使自身利益最优化,理性的参与者根据收益的大小,可能会在协议开始时就拒绝参与协议,也可能替代他们的本地输入,在得到计算结果后,也可能早期中断协议.或者合谋偏离协议.但是,如果诚实地遵守协议是参与者最优策略的话，那么参与者将没有偏离协议的动机,为了使参与者具有合作的动机,本节构建的电路概率效用模型如下.

我们用ai表示参与者Pi的策略,a=(a1,···,an)表示所有参与者的策略组合,a-i表示除Pi外其他人的策略,()=(a1,···,ai-1+1,···,an)表示参与者Pi的策略改为,r为参与者行动组合最后出现的结果,info(r)是一个多元组(s1,···,sn),其中如果si=1,表示Pi获得计算输出,否则表示没有获得,我们让infoi(r)=si表示用num(r),表示了解计算结果的人数,那么有如下效益假设:

(1)如果info(r)=info(r′),那么ui(r)=ui(r′);

(2)如果info(r)＞info(r′),那么ui(r)＞ui(r′);

(3)如果info(r)=info(r′)且num(r)＜num(r′),那么ui(r)＞ui(r′).

即在安全多方计算中,理性的参与者首先想了解计算结果,然后希望越少的人了解计算结果越好.这保证了只要参与协议的收益足够大,那么理性的参与者就有参与协议的动机.用U+,U,U-,U--表示参与者在以下几种情况下的收益:(a)当r表示Pi了解秘密信息,而其他参与者不了解秘密信息时,那么ui(r)=U+;(b)当r表示Pi了解秘密信息,而至少有一个其他参与者也了解秘密信息时,那么ui(r)=U;(c)当r表示Pi不了解秘密信息,其他参与者也不了解秘密信息时,那么ui(r)=U-;(d)当r表示Pi不了解秘密信息,而至少有一个其他参与者了解秘密信息时,ui(r)=U--.他们间的关系是U+＞U＞U-＞U--.

本文所设计的模型采用了多轮博弈,并且不让参与者知道博弈何时结束.为了及时的发现参与者欺骗,在每一轮中利用可验证的方法对参与者的行为和策略进行检验.将秘密s∈Zq放在某一轮中,用k表示,其余的为无意义的测试轮.当协议在第r轮时,如果其他参与者采用指定的策略σ-i(即诚实的发送子秘密的份额),而参与者Pi采用策略进行欺骗,用cheat表示这个基本事件.当r＜k,用early表示,此刻,Pi只能通过猜测秘密进行欺骗;当r=k,用exact表示,即Pi正好在第k轮偏离协议;当r＞k,用late表示,即参与者在k轮之后进行欺骗;correct表示Pi输出了正确的秘密值;Pr[·]表示事件发生的概率.那么参与者Pi在第r轮欺诈的期望收益为:

且

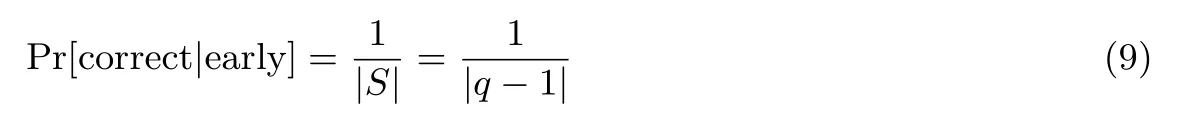
(因为s∈Zq),及可得:

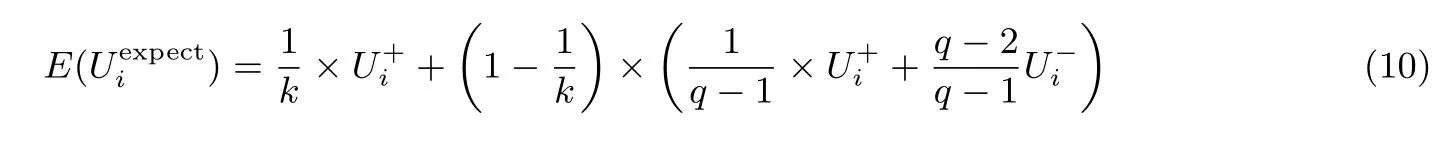
由此可知如果满足式(11)

则协议能够保证博弈达到均衡状态,使得参与者不会背离协议,从而正确的执行协议.

3 Beaver构造的有偏向投币协议

在Beaver构造的有偏向的投币协议[19]中,设d是明确公平性约束的参数,令R(x1,···,xn)=x1⊕···⊕xn.如果对于任意xi是均匀随机比特,那么R也是均匀随机的比特.对于ϕ功能来说,如果x1+···+x2kd≥kd+1,那么ϕ(x1,···,x2kd)=1,否则ϕ=0.如果ϕ的输入是均匀随机的,那么输出则是以概率偏向0.协议伪代码如算法1.

代码中EVALUATE功能表示安全多方计算功能,详细内容请参考文献[19].协议的思想是产生一系列偏向0的投币,然后将投币值和计算值异或,诚实者能够及时发现恶意者中断协议或者有欺骗的行为并且此时所有参与者获得的信息量基本相等(最多差一个采样点).但是Beaver的协议仅适用于布尔类型的函数值,为了能将其扩展到多方求和协议,本文结合博弈论的思想改进了Beaver设计的协议,根据参与者的收益函数,生成一个随机字符串,利用随机字符串隐藏多方求和的值,然后参与者按位揭示随机串,最终恢复求和的值.

4 基于电路计算的理性安全多方求和协议

在我们的协议中,除保证参与者有执行协议的动机之外,还有以下要求:(1)保证每个理性的参与者的输入需要独立于其他参与者的输入;(2)在每个阶段,保证合谋集团都能发送正确的信息;具体步骤如下.

Algorithm 1:有偏向的投币协议for l=1,···,k3d do for m=1,···,2kd do Each player i chooses a random bit bim.Run EVALUATE-R(b1m,···,bnm),and let cm be the output.end Enddo Run EVALUATE-ϕ(c1,···,c2kd)to obtain a secret,biased coin,ej.Run EVALUATE-exor on V and ej to obtain the masked result rj.Each player i broadcasts his piece of rj.Each player i interpolates rj if n-t pieces have been broadcast,otherwise he outputs cheating.end Enddo Output:Majority(r1,···,rk3d)

(1)根据所求功能,首先设计相应的逻辑电路,假设有m个参与者,Pi(i=1,···,m)的输入串为希望电路输出得到为了描述方便,本文首先设计了有两个参与者的两方安全求和电路,每个参与者输入为2位的电路,如图3,其中表示xi的最低位,y0表示电路求和值f(x1,···,xm)的最低位.其次设计了4个参与者的四方安全求和电路,每个参与者的输入为2位的求和电路,如图4.对于n人多位的电路可以类推设计.

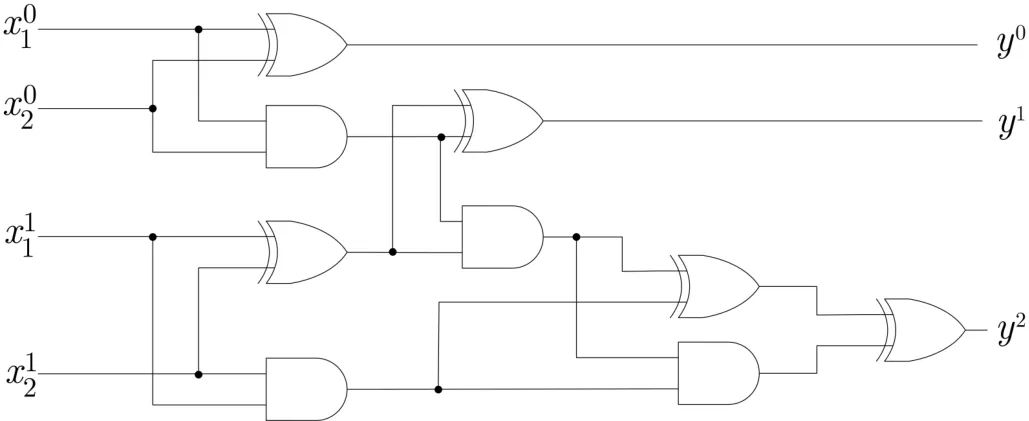
图3 两方安全求和电路Figure 3 Two-party secure sum circuit

(2)利用传统的多方计算协议产生一个随机二进制串R(可以将R视为一个向量),|R|取决于参与者的效益且满足具体过程如下:每个参与者随机选择一比特σi,令功能Coin-gen(σ1,···,σn)=σ1⊕···⊕σn,运行传统的GMW多方电路计算[18]产生一系列投币(承诺但隐藏的)br=Coin-gen(σ1,···,σn),令br(1,···,|R|)为第r个比特.这样,每个参与者拥有R串中每一位比特的子份额.

(3)利用传统的GMW多方电路计算[18]输出f(x1,···,xn)+R的子份额,此时,如果每个参与者将子份额发给其他参与者,不会对公平性造成影响,因为有随机数R对f(x1,···,xn)进行了随机隐藏,这样,每个参与者获得f(x1,···,xn)+R的值.

(4)然后循环|R|轮来取得R中的每一位,获得的具体步骤如下:在r(1,···,|R|)轮,利用Beaver等[19]投币协议来揭示R中的每一位br.具体如下:循环k3d次,每次运行EVALUATEϕ(c1,···,c2kd),获得概率偏向0的投币ej,运行多方电路计算,每个参与者获得ej⊕br的子份额,然后每个参与者依次发送子份额,循环k3d之后,参与者可以获得k3d个采样点,根据0和1数量的多数原则可确定br的值,通过|R|轮循环后,所有参与者都能获得R.最后,和前面获得的f(x1,···,xn)+R相减,即每个参与者可公平地得到求和值.

(5)为了保证参与者能诚实的执行协议,利用GMW编译器,对以上每一步骤进行编译.

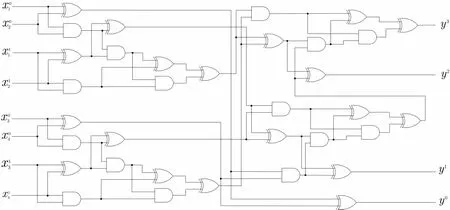
图4 四方安全求和电路Figure 4 Four-party secure sum circuit

5 协议分析

定理1在基于电路计算的安全多方求和过程中,参与者在获得最后求和结果时,不会泄露自身的隐私输入.

证明:在一个逻辑电路计算中,假设有m个参与者,Pi(i=1,···,m)的输入串为{0,1}n,每个参与者分割每一位输入,对于每个数字i=1,···,m,j=1,···,n和k/i,Pi随机选择一位发送Pi,使其为第(i-1)n+j根电路输入线值的子份额,而Pi的子份额为由于任何逻辑电路都可以由与门和一个异或门组合实现,而与门代表乘法门、异或门代表加法门,所以只需考虑这两种门的计算即可.因为不经意传输协议在多方安全计算中占有至关重要的作用,下面考虑加法门和乘法门的计算.

在逻辑电路中加法门的计算,每个参与者将zi=ai+bi作为逻辑加法门输出线值的子份额,这些子份额满足: 可以看到这正是理想的值,所以加法门平凡地满足要求.

在逻辑电路中乘法门的计算,如果仍采用上面的方法来计算乘法门,计算结果则不符合要求,下面看一下通过乘法门进行计算后所得结果:

从式(13)看出,Pi知道ai,bi,而可以由Pi和Pj执行安全两方电路计算获得,计算过程如下:

Pi随机选择一位比特ci,并将ci作为与门输出线值的子份额即另外Pi准备四个值Pi和Pj执行不经意传输协议.

调用不经意传输协议后,Pj得到与门输出值的子份额,即

下面分四种情况讨论:

(1)当(aj,bj)=(0,0)时,令=ci+(ai+0)·(bi+0),即=,这时满足式(14):

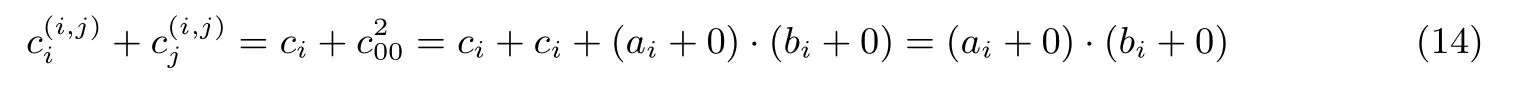
(2)当(aj,bj)=(0,1)时,令即=,这时满足式(15):

(3)当(aj,bj)=(1,1)时,令即=,这时满足式(16):

(4)当(aj,bj)=(1,0)时,令即=,这时满足式(17):

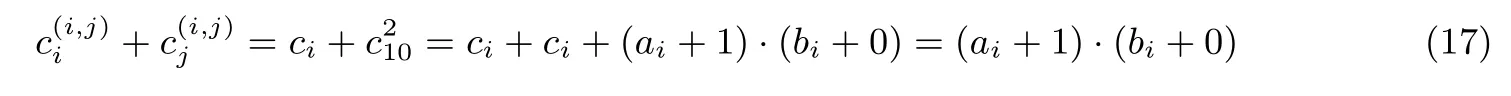
我们可以看到经过与门的计算P1得到得到,满足式(18):

下面Pi将作为乘法门输出线的子份额,可知乘法门满足式(19):

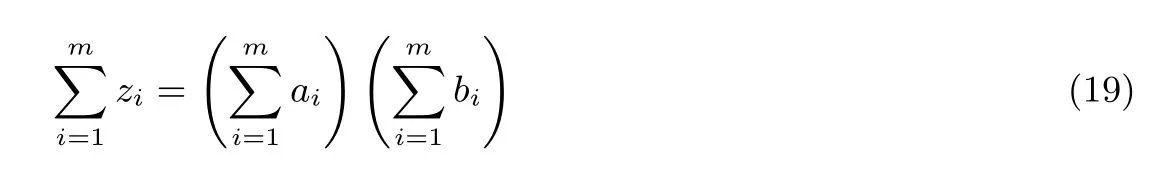
将加法门和乘法门组合后,就形成了一个逻辑求和电路,通过对逻辑电路中的每一个逻辑门运算,Pi会获得电路输出线的子份额si.最终,Pi将自己的电路输出线的子份额si发给其他人,这样每个人都能够得到电路计算结果

定理2方案在满足式(21)的条件下,参与者没有合谋偏离协议的动机,协议能保证公平性.

证明:在方案中,每一个合谋集团C⊂[n],|C|≤m-1中的合谋者不能通过合谋获得R,如果合谋者通过猜测R,猜对的概率为合谋者Pi获得效益为.猜错的概率为1-,合谋者Pi获得效益为合谋者Pi的期望收益为

而当

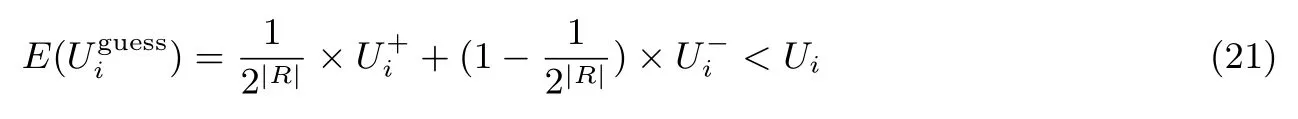
即

也就是当

时,参与者没有偏离协议动机,当参与者执行协议第四步,在取得R中的最后一位时,如果合谋者提前中断协议,将会使得所有参与者有的概率获得R,这里有两种情况:一种是合谋者在诚实者前面发送子份额,另一种是合谋者在诚实者之后发送子份额.在第一种情况中,当合谋者中断协议时,合谋者和后发送子份额的诚实者了解的信息采样点相同.在第二种情况中,当合谋者中断协议时,合谋者比先发送子份额的诚实者多了解一个信息采样点(信息量几乎相等).所以合谋者没有偏离协议的动机,最终每个参与者都能公平的得到计算结果.

6 小结

本文结合密码学与博弈论,对安全多方求和过程中,参与者遵守和背离协议的策略、效益进行了分析与设计,构建了一种安全多方求和电路的概率效用模型.我们所设计的理性安全多方求和协议消除了成员欺诈的动机并且不需要拥有大多数诚实参与者这个强条件,解决了参与者在多方求和计算过程中合谋问题,能够保证每个成员在标准点对点通信网络下公平地获得求和结果.