博弈论在区块链中的应用研究*

宋丽华,李涛,王伊蕾,2

1.鲁东大学 信息与电气工程学院,烟台 264025

2.曲阜师范大学 信息科学与工程学院,日照 276826

1 引言

博弈论(game theory)主要研究整个博弈中激励结构件的相互作用,根据是否可以达成具有约束力的协议,博弈可以分为合作博弈(cooperate game)和非合作博弈(non-cooperate game)[1].合作博弈指的是博弈环境中的某些(或者全部)参与者以同盟、合作的方式进行博弈,研究的是参与者的收益分配问题.非合作博弈则把所有参与者的行为都看作是单独的行为,与环境中的其他参与者无关,研究的是参与者在利益相互影响的局势中如何选择决策使自己的收益最大,即策略选择问题.现实中的绝大多数博弈会包含参与者之间的合作和冲突行为,因此通常看作是合作博弈与非合作博弈的混合物.博弈论广泛应用于经济学、管理学、社会学、政治学、军事科学等领域.近年来,博弈论在密码学领域引起了研究学者的重视,催生了博弈密码学的新兴交叉学科:理性密码学[2-5].例如,传统密码协议中的参与者被分为诚实参与者,半诚实参与者和恶意参与者,而理性密码协议中参与者被认为是理性的.博弈论在密码学领域的研究主要集中在理性多方安全计算领域,利用理性参与者最大化其收益的特性,约束他们的行为,促使他们选择合适的策略保证协议的安全性,多数情况下用来解决公平性[6-8].然而,理性多方安全计算中最大的一个瓶颈就是理性参与者的动机,即收益函数的定义.目前大多数理性协议中理性收益函数都来源于某个已知博弈(例如囚徒困境博弈、连锁店博弈),然后再根据具体协议定义每个参与者的收益函数.这些收益函数的定义诟病在于,缺乏足够的经济动机作为理性参与者收益函数的支撑.

安全多方计算中公平性指的是敌手和诚实参与者同时获得输出,然而Cleve指出,当敌手控制的参与者超过半数以上时,公平性是不可能实现的[9].因此,针对公平性实现的研究一直被忽视.博弈论的引入解决这个问题,收益函数为理性参与者提供了诚实参与安全多方计算的动机,纳什均衡将理性参与者的策略约束在协议允许范围内,使得诚实参与者都可以获得输出,实现公平性.然而,理性安全多方计算中的收益函数,貌似专门为实现公平性精心设计的,缺乏真实的背景环境支撑.为了解决这个问题,学者们从经济学角度出发,将比特币(Bitcoin)[10,11]中的经济激励引入安全多方计算中,为参与者参与安全多方计算协议提供了充分而又真实的动机,基于比特币的安全多方计算也可以实现公平性[12].另外,比特币本身就是一种货币,用博弈论来分析其中的激励机制是一种必然的方式.博弈论中的合作博弈和非合作博弈可以用来分析矿池策略的设计.总之,博弈论、比特币和安全多方计算之间联系紧密、互相渗透,其连接纽带就是参与者的动机,他们之间的关系如图1所示.

2 博弈论、比特币和安全多方计算之间的关系

2.1 理性安全多方计算

理性安全多方计算(rational secure multi-party computation,RSMPC)是博弈论和安全多方计算的一个综合,利用博弈论中的一些概念和方法解决安全多方计算中的某些问题[13-15].在RSMPC中,参与者被看作是理性的或自私的,称为理性参与者(rational parties),以追求利益最大化为行为的动机.按照博弈论的方法,参与者的“利益”用所谓“效用函数”描述,理性安全多方计算协议的执行,就是理性参与者根据其效用函数的定义,以最大化效用为目的,使用各自的策略进行多轮交互的过程.传统的“诚实参与者”和“敌手”均可看作是特殊的理性参与者.换句话说,协议的执行就是理性参与者采取一系列策略的过程,理性参与者可以遵循协议,也可以偏离协议.遵循协议或偏离协议都取决于他们能否最大化其效用.协议设计的最终目标是:每个参与者都遵循协议,都没有偏离协议的动机.从博弈论的角度解释这一目标就是:每个参与者都遵循协议可以达到纳什均衡(Nash equilibrium),没有一个参与者可以通过偏离它而获得更高的效用.

图1 比特币、博弈论和安全多方计算之间的关系Figure 1 Relationship among Bitcoin,game theory,and secure multi-party computation

2.2 基于比特币的安全多方计算的研究进展

比特币作为一种电子货币可以解决参与者的动机问题[16,17],其中理性参与者参与多方计算的动机可以理解为要么获得计算结果,要么获得一些经济补偿(例如比特币).Bentov和Kumaresan[18]定义了几个理想元语(ideal primitive):认领或退款函数性(claim-or-refund functionality)[19],带惩罚的安全计算(secure computation with penalties)和带惩罚的安全彩票(secure lottery with penalties).他们构造的多方计算协议只需要调用常数次即可.Kumaresan和Bentov研究了如何使用比特币激励参与者实现正确计算[20],他们的工作包括四个方面:

(1)可验证云计算(verifiable computation):委托人把一个计算外包给云服务器,如果云返回了正确的计算结果,委托人就支付给云服务器一定的酬劳.他们设计了一个协议可以实现公开和私有验证机制.

(2)带有限制泄露的安全计算(secure computation with restricted leakage):基于Huang et al[21]的工作他们提供了一个高效的安全计算协议,一旦恶意敌手被发现试图获得1比特的信息,都会受到惩罚(例如扣除比特币).

(3)公平安全计算(fair secure computation):当参与者提前中断协议时,会受到金钱方面的惩罚.他们在比特币网上构造了一个常数轮的理想交易函数性(ideal transaction functionality),并且基于该函数性设计了一个混合世界下的常数轮安全计算协议.

(4)非交互式悬赏(non-interactive bounty):他们提供了一个基于比特币网络的非交互式捐款机制,使得领赏人只要完成既定任务就可以领到赏金.

Kumaresan等还讨论了如何利用Bitcoin实现去中心化扑克[22].2017年Kumaresan等又分别对CRYPTO 2014[18]和CCS 2015[22]中的方案进行了改进[23],提出如何利用惩罚机制优化安全计算模型.Kiayias等提出了使用区块链来实现公平且具有健壮性的多方计算协议[24].他们的工作包括以下三个方面:(1)提出了一个带有补偿的安全多方计算的形式化模型;(2)该模型是UC安全的[25];(3)首次提出了一个常数轮健壮性多方计算协议.

2.3 基于博弈论的比特币协议

从经济学角度上看,比特币中的激励机制解决了挖矿者的动机问题,而博弈论在经济学领域的应用已经非常成熟,因此从博弈论的角度分析比特币和区块链中的一些问题水到渠成,更加方便.众所周知,比特币中最重要的一个机制就是挖矿(mining).Tschorsch和Scheuermann给出了比特币的基本概念和工作流程[26].矿工想要获得比特币就需要解决特定的数学难题,即,找到一个比特币区块,矿工就可以获得12.5个比特币.截止到2018年12月23日,一个比特币的价值为27 706.77元人民币.因此,挖矿的收益还是很可观的,这为矿工提供了最足够的挖矿动机.然而解决这些难题需要具备一定的计算能力,通常单个矿工需要花费几个月甚至几年才能挖到一个比特币区块.然而比特币网络大概10分钟就会出现一个新的区块,所以大部分的矿工徒劳无获.为此,部分矿工组成矿池(mining pool),将他们的计算能力作为一个整体,如果在合适时间内挖到一个有效区块,他们就按照每个人的计算能力分享挖矿所得的奖励.然而,从博弈论的角度出发,如果激励机制设计有漏洞,导致偏离矿池策略能够带来更大的收益,理性的矿工都有偏离矿池策略的动机,这与博弈论中合作博弈与非合作博弈相似.

Schrijvers等从博弈论角度出发,在单个矿池中定义了一个矿池支付函数[27].矿池中的矿工一旦挖到一个区块,可以选择何时向矿池管理员报告.他们定义了支付函数的三个特性:激励相容(incentive compatibility),按比例支付(proportional payments)和预算平衡(budget balanced).Schrijvers等分析了目前几种矿池分配策略的支付函数是否满足这几个特性.按算力比例分配的支付函数(proportional reward function,记为Rprop)指的是按照每个矿工的计算能力来分配收益,这是一种较早的矿池分配策略.然而Rprop满足按比例支付和预算平衡的特性,但它不是激励相容的.按份额比例分配的支付函数(per-per-share reward function,记为Rpps)满足激励相容的特性,但不满足预算平衡的特性.因此Schrijvers等提出了一个新的激励相容支付函数(incentive compatible reward function,记为RIC),该支付函数不仅考虑到每个矿工的份额还考虑到发现区块者的身份,使得收益分配更加合理.他们证明RIC满足激励相容,按比例支付和预算平衡这三个特性.但是矿工不允许加入到其他矿池或者独立挖矿,他只能在矿池中贡献自己的份额,也没有考虑矿工的合谋问题.Eyal和Sirer研究了比特币协议的激励相容问题[28],在允许矿工合谋的情况下,理性矿工(rational miner)最终会变成自私矿工(selfish miner),这些自私矿工合谋组成一个自私矿池(selfish pool),能够吸引越来越多的自私矿工加入,最后矿池会变成控制超过多数矿工的一个矿池,比特币又变成了一种中心化货币,这违背了比特币的初衷.也就是说任何一个自私矿池都可以发展为一个控制绝大多数矿工的自私矿池,从而破坏比特币的去中心化.这种攻击称为自私挖矿攻击(selfish mining attack).为了抵御这种攻击,他们提出了一个比特币协议的改进版本,这个新版本是逆向兼容的(backwards-compatible).当矿工发现区块有两个相同长度的分叉(fork)时,同时在全网广播他们并且随机均匀地在这两个分支上继续挖矿.改进版本的比特币协议可以阻止那些控制少于1/4资源的自私矿池成为一个控制绝大多数资源的矿池,优于改进之前的门限值0.Nayak等扩展了挖矿策略的空间[29],其中包括了“顽固”策略(“stubborn”strategies),他们证明了对于较大规模的策略空间来说自私挖矿并不是一个好的策略.Nayak等主要研究了两类挖矿攻击:类自私挖矿攻击(“selfish-mining”-style)和网络层次的攻击,又称之为日食攻击(eclipse attack).一个矿工可以将挖矿供给和网络层次的日食攻击结合起来增大他的收益.也就是说,当给定最优策略时,某些日食攻击的受害者可以在攻击过程中受益.

Heilman引入了首选重置(freshness preferred,FP)机制[30],该机制通过使用不可伪造时间戳来惩罚那些不及时释放区块的自私矿工.他们将Eyal和Sirer[28]中的门限由0.25提升至0.32.然而该机制不是激励相容的,而且对于可伪造的时间戳不具备健壮性.也就是说FP机制的实现依赖于不可伪造的时间戳,但是不可伪造的时间戳又很难实现[31,32],因此该机制的实现具有一定的局限性.Solat和Potop-Butucaru针对自私挖矿攻击和截留攻击(withholding attack)提出了一个解决方案:ZeroBlock[33],该方案不需要使用时间戳(timestamp)技术,因为时间戳可以被伪造.在ZeroBlock方案中,如果一个自私矿工持有区块的时间超过幅度间隔(mat interval),例如,最大的可接受一个新区块的等待时间,那么诚实矿工就会拒绝接受这个新区块.

Sapirshtein等扩展了文献[28]的工作,提出了一个高效算法[34],该算法可以计算ε-optimal的自私挖矿策略,其中ε＞0.他们证明了算法的正确性,并分析了其误差范围.使用这种高效算法,矿工可以计算自私挖矿策略获得更大的收益,而且自私矿工需要控制的资源也少于1/4,也就是说攻击者及时控制的资源少于1/4也有利可图,这样就增加了攻击者的能力,使他们有机可乘.他们还证明如果考虑区块在网络传播中的延迟,门限值又变为0,即,攻击者不论控制多少资源,总存在一个自私挖矿策略,其带来的收益高于诚实挖矿的收益.最后他们总结了自私挖坑和双花(double spending)之间的相互作用.文献[27,28,34]讨论的都是一个矿池对诚实矿工的攻击.Eyal讨论了两个矿池之间的攻击[35],两个矿池之间存在个人理性与集体理性的矛盾,这类似于公共地悲剧博弈.Eyal提出了两个矿池之间的截留攻击,一个攻击矿池(attacking pool)的管理者首先在另一个受害矿池(victim pool)注册为正常矿工,他从受害矿池接受若干任务并把这些任务指派给攻击矿池中的渗透矿工(称之为infiltrating miners),渗透矿工在攻击矿池中的比例称之为渗透率(infiltration rate).攻击矿池会把渗透矿工的部分工作能力提交给受害矿池,让受害矿池评估渗透矿工的能力,当渗透矿工提交完全的工作证明时,攻击矿池忽略这些工作.截留攻击的缺陷在于受害矿池的总体计算能力没有增加(渗透矿工不工作),但是它的平均预算却降低了.一方面攻击矿池分出一部分计算能力给受害矿池,其自身的计算能力也受到了损害.因此,总体来说截留攻击降低了整个网络的计算能力.对于两个矿池来说,采取截留攻击是唯一的纳什均衡,然而如果双方都不采取截留攻击,他们的收益会更大.从博弈论角度分析,是否采取截留攻击对矿池来说是一个矿工的困境(miner’s dilemma),矿工不断的挖矿过程就类似与一个重复囚徒困境博弈.Rosenfeld建议修改区块结构来解决这一问题[36].

在挖矿过程中,除了是否构建自私矿池以及合适释放新挖区块等问题,还有很多更加细致的问题有待探索.如果矿工在一个区块中包含更多的交易,一旦他挖出一个新的区块,他获得的交易费就会更多.但是如果他们的区块中包含较少的交易,他们的区块在整个网络中传播的时间就会较低,这可以提高他们区块到达其他节点的速度.因此包含多少交易对于矿工来说也是一个难题.Houy在矿工之间定义了一个比特币挖矿博弈(Bitcoin mining game)[37],假设包含在一个区块中的交易(transaction)条数是一个博弈的结果(outcome),研究了博弈的纳什均衡.Houy讨论了从经济学角度研究交易费对比特币区块规模(block size)的影响[38],任何一个拥有固定交易费的情况,都可以等价转化为设置一个区块允许的最大规模(maximum block size)问题.而且给交易规定一个固定交易费就相当于给每一个交易强制收税,这无疑会破坏比特币的经济生态环境.但是如果不对每个区块的最大规模加以限制,交易费又会降为0,这样矿工都没有挖矿的动机.当一个矿工试图挖掘新区块时,交易已经存在于网络中,这种情况下,矿工类似于斯塔克伯格博弈(Stackelberg game)中的跟随者,在自己有限的区块规模中,为了最大化自己的收益,矿工的动机是在区块中包括尽可能多的交易1关于比特币安全的详细内容,读者可以参阅文献[39]..

3 智能合约与博弈论

1996年尼克·萨博(Nick Szabo)提出了智能合约的概念,“一个智能合约是一套以数字形式定义的承诺(promises),包括合约参与方可以在上面执行这些承诺的协议.”事前合约参与方制定承诺,智能合约在满足触发条件后自动执行,事后任何参与方都无法更改合同承诺.智能合约能够自动执行,无需事前审查和预付高昂违约成本,避免了合同纠纷等棘手问题[40].但是因为缺乏行之有效的技术支撑和信任平台,智能合约迟迟未能应用到实际产业中.以太坊(Ethereum)借鉴了区块链技术去中心化、不可篡改性、过程透明可追踪等特性,为智能合约提供了一个可实施的开发平台[41].以太坊提供了图灵完备(Turing complete)的脚本语言,能够嵌入更多额外信息.因此,任何智能合约一旦被精确定义,就可以在以太坊上构建并自动实施.在以太坊系统的支持下,智能合约迅速应用到数字社会的各个领域.2016年12月由数字商务商会(Chamber of Digital Commerce)和智能合约联盟(Smart Contracts Alliance)共同发布的“智能合约:12种商业及其他使用案例”(Smart Contracts:12 Use Case for Business & Beyond)白皮书中指出,智能合约可以应用在包括抵押贷款、物联网[42]、医疗研究等诸多领域[43].

3.1 智能合约中的安全问题

智能合约的安全问题可以概括为两个方面:内部安全和外部攻击.Luu等介绍了一种新的智能合约安全问题,并且提出了一种加强智能合约鲁棒性的方案[44].Kosba等提出了一个去中心化系统:Hawk,该系统主要解决智能合约内容的隐私性问题[45].Bhargavan等将智能合约编译成F*语言,验证了智能合约中的运行时间安全和智能合约的正确性问题[46].Atzei等针对以太坊上的智能合约进行了总结[47],他们主要关注了合约的健壮性,并且分类叙述了程序中的陷阱(programming pitfalls).Dika对所有已知合约的脆弱性进行了分类总结[48],他们还分析了以太坊上的智能合约(例如Oyente,Security和SmartCheck)中代码安全问题.最近,Nikolic等对近百万份智能合约进行了分析[49],发现其中有34 200份智能合约本身具有一些脆弱性,很容易受到黑客的攻击.另外,他们还利用MAIAN这个工具对智能合约的有效性进行了分析.在对3759份智能合约抽样调查后发现,其中有3686份智能合约含有漏洞,包含漏洞的概率高达89%.智能合约的漏洞还会造成客户电子财产被锁死在以太坊中,在2017年11月就有媒体爆料,因为一些以太坊智能合约使用者的误操作,导致了约3亿美元永久被冻结在以太坊之中.

除了智能合约本身具有一些安全问题外,专门针对智能合约的攻击也有很多.Velner等介绍了一种基于智能合约的攻击模型[50],攻击者通过智能合约可以破坏矿池的正常工作.Juels等提出了犯罪智能合约(criminal smart contract)的概念[51],犯罪分子可以利用智能合约实施一些违法活动,例如非法售卖盗版影片.他们着重讨论了刑事智能合约的可行性以及危害性,文章的最后他们呼吁出台相关的法律政策以及提高技术防范措施.Alharby和van Moorsel甚至认为目前没有合适的方法阻止犯罪智能合约[52].目前的研究加剧了人们对智能合约所带来危害的担忧,学者们试图寻找其他方法研究如何抵御智能合约带来的负面作用.Bigi等综合了博弈论和形式化分析方法(formal method)验证了智能合约的有效性[53].他们主要分析了由智能合约引入的保证金(deposit)对系统带来的不确定性,进而研究了如何提高智能合约的有效性.

3.2 基于博弈论的智能合约

尽管智能合约还不完美,存在各种安全问题,但是它的应用范围依然很广泛.在服务外包云服务中,如果试图付费最小,委托人(client)通过付费(pay as you go)的形式把服务外包给一个云计算.例如,委托人将自己的输入x发送给云,云负责计算f(x).云诚实计算f(x),计算的花费是c,随后云将结果返回给委托人,委托人支付酬劳r.至此为止,云计算的外包服务结束,云的收益是r-c.云计算正常结束的前提条件是云是诚实的,一旦云是恶意的或者被其他实体腐败(corrupted),外包服务的安全性就存在隐患.例如,云为了最大化其收益,令f(x)等于一个随机数并将其返回给委托人.委托人无法验证返回值的正确性,因此委托人默认返回值为正确的,此时云得到收益r,大于正确计算时得到的收益.也就是说如果将计算外包给一个云,该云为了最大化其收益,具有欺骗委托人的动机.为了解决这个问题,可以采用Set@Home的方法,将计算委托给多个云,每个云返回一个计算值,当大多数云的返回结果达到一致时,委托人认为该值是正确的,支付给每个云一个费用.这种方法可以很好地解决计算结果正确性的问题.但是存在两个问题:(1)委托人的花费较高;(2)一旦大多数云合谋,委托人仍然无法得到正确值.

Dong等针对这个问题[54],结合智能合约和博弈论,提出了可验证云计算中抗合谋的智能合约.他们假设委托人和云都是理性的参与者,委托人在保证计算结果正确性的前提条件下,力争最大化其收益.因此他把计算外包给尽可能少的云以减少其支出,在这里Dong等选择了两个云做相同的计算.在云和委托人之间建立一个囚徒智能合约(记为Prisoners’smart contract),它的主要作用是完成保证金和报酬的交易,从而保证两个云诚实地完成计算.然而从两个云的角度考虑,他们有充分的动机达成合谋,因为合谋的收益明显大于不合谋的情形.如果双方希望达成合谋,就需要签订一个合谋智能合约(Colluders’smart contract),一旦有一方违反合约,将会受到惩罚.他们可以成功地用一个随机数合谋欺骗委托人.委托人最终花较高费用得到一个随机数,与此同时,两个云不需要任何计算就可以获得酬劳.这对委托人来说显然不公平,因此委托人需要采取一些措施阻止两个云的合谋.Dong等在委托人和某个云之间构造了一个背叛智能合约(Traitors’smart contract),通过给某个云提供一些奖励机制，阻止两个云之间的合谋.至此,在囚徒智能合约、合谋智能合约和背叛智能合约的相互作用下,给定合适的参数设置,两个云没有合谋的动机,最终诚实地完成计算.

4 犯罪智能合约的有效性研究

Juels等提出的犯罪智能合约的概念[51],其中包括一个智能合约PublicLeaks,不法分子可以利用该合约出售一些非法文件,例如盗版影片.PublicLeaks首先将影片割分成若干小片段,为了验证依赖于智能合约收集捐款,当捐款金额达到一定数量时,释放影片的所有权.Juels等人分析了PublicLeaks,分析了这个智能合约的可行性,但是他们没有讨论PublicLeaks的运行条件.例如,他们规定当捐款金额达到一定数量时,Dealer可以非法售卖盗版影片.但是他们没有讨论观众的捐款动机,有没有涉及在什么条件下捐款金额能够达到一定数量,观众的捐款动机对于智能合约的执行有何影响,有什么因素对PublicLeaks的可行性产生影响.为了解决这个问题,我们借鉴文献[53]的思路结合形式化方法,在PublicLeaks中引入了一些随机变量,重新构造了一个智能合约Random-PublicLeaks.随机变量的含义如表1所示.

表1 Random-PublicLeaks中的变量列表Table 1 Parameters list of Random-PublicLeaks

智能合约Random-PublicLeaks的详细流程如图2所示.

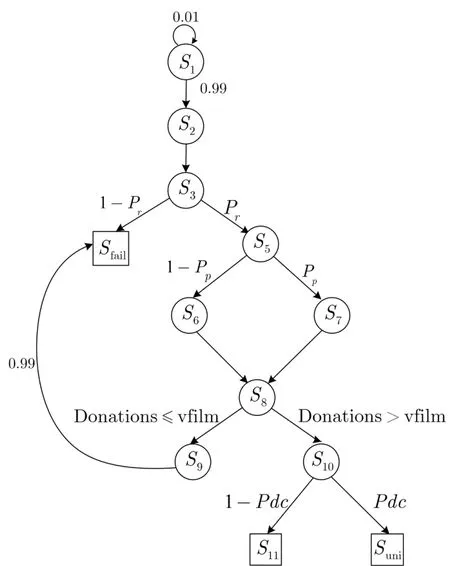
图2 智能合约Random-PublicLeaks的基本流程Figure 2 Basic flow of Random-PublicLeaks

(1)状态S1:Dealer将影片film分割成n个片段filmi(i∈[1,n]),他使用密钥ski把每一个片段加密.与此同时Dearer需要提交部分保证金,如果他不提交保证金(假设概率为0.01),状态就维持在S1,否则就转入状态S2.

(2)状态S2:感兴趣的观众下载所有的加密片段c={ci}i∈[1,n]={Encki(fi)}i∈[1,n].

(3)状态S3:合约随机地在[1,n]中选择一个子集n′,然后Dealer被要求解密n′所对应的片段.如果Dealer不能够正确解密这些片段,那么合约就转入最终状态Sfail.否则转入状态S5.

(4)状态Sfail:Dealer的保证金被扣除,智能合约终止.

(5)状态S5:一旦Dealer正确解密n′所对应的片段(说明Dealer拥有解密整个影片的能力),观众选择捐款或者不捐款.如果不捐款就转入状态S6,否则转入状态S7.

(6)状态S6:观众不捐款,转入状态S8.

(7)状态S7:观众捐款amt,转入状态S8.

(8)状态S8:假设捐款观众数为k,Dealer从他们那里收集到总的捐款额为Donation=k×amt.捐款额和影片价值之间满足关系Donation≤vfilm,则转向状态S9,否则转向状态S10.

(9)状态S9:Dealer没有解密影片的动机,转向状态Sfail.

(10)状态S10:Dealer解密影片,转向状态Suni.然而对于非理性的Dealer来说,他仍然会以很小的概率(例如1-Pdc)错误地解密影片,导致状态转入S11.

(11)状态S11:返还Dealer的保证金,合同终止.

(12)状态Suni:Dealer得到捐款并且返还了保证金,观众(不论捐赠与否)可以解密所有片段.

我们采用PRISM进行了方针,PRISM是一款用于概率模型检测(probabilistic model checking,PMC)的开源工具,PMC是一种验证存在随机行为系统的分析技术,可以应用在安全领域,例如概率合约签署、概率公平交换和博弈论,例如市场投资预测、稳定匹配.Bigi等综合了博弈论和形式化分析方法利用这个工具对智能合约中Deposit进行了仿真[53],讨论了如何设置Deposit的值来促进合约的执行.本文也利用这个工具,对于各个随机参数对于犯罪智能合约的有效性进行了仿真.当给定Pr=0.9,Pp=0.7,amt=30,vfilm=30,k=10时,智能合约单次运行时各个参数的变化情况如表2所示.

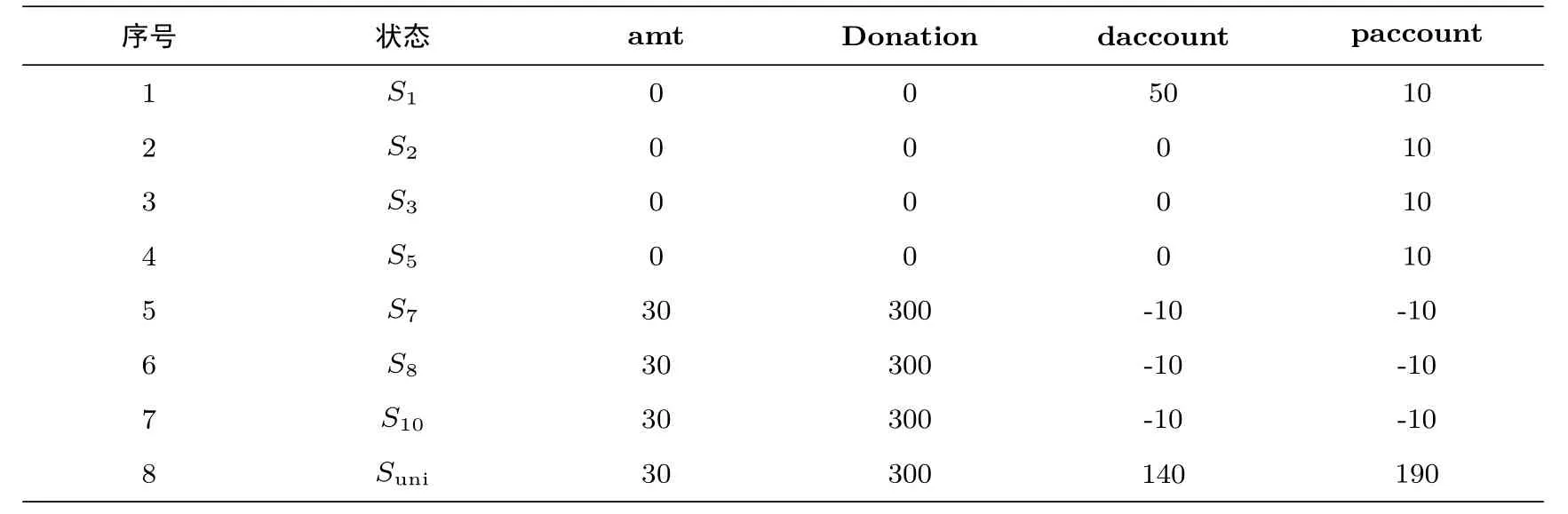
表2 智能合约运行过程中参数的变化情况Table 2 Parameters in smart contract

从表2可知,因为存在随机变量,合约运行到每个状态的情况不同,导致每次参数有波动.即使捐款额达到一定金额,Dealer的余额也会发生波动,这是因为每个状态对于余额的处理不同,Dealer余额随时间变化的情况如图3所示.

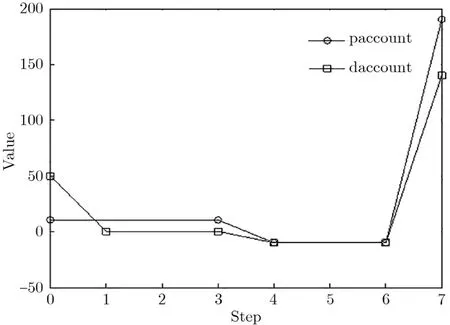
图3 Dealer余额随时间的变动情况Figure 3 Fluctuation of balance

Juels等的研究结果表明[51],Dealer可以通过犯罪智能合约非法卖掉盗版影片.也就是说,智能合约达到状态Suni,但是他们没有研究到达这个状态的概率.本文研究了在各个参数下,智能合约Random-PublicLeaks到达状态Suni的最大概率.我们首先设定Pr=0.8,Pdc=0.8,amt=10,vfilm=200,Donation=k×10,仿真结果如图4所示,当Pp固定时,能否到达12的最大概率只与k的值有关.而当k值固定时,Pp越大,到达12的概率也越大,最大是65%.刚刚超过50%,所以说,即使所有的参与者都捐赠,也未必一定能达到状态Suni.因此可以看出Dealer使用智能合约贩卖盗版影片的成功率较低,犯罪智能合约的有效性制约了其应用.

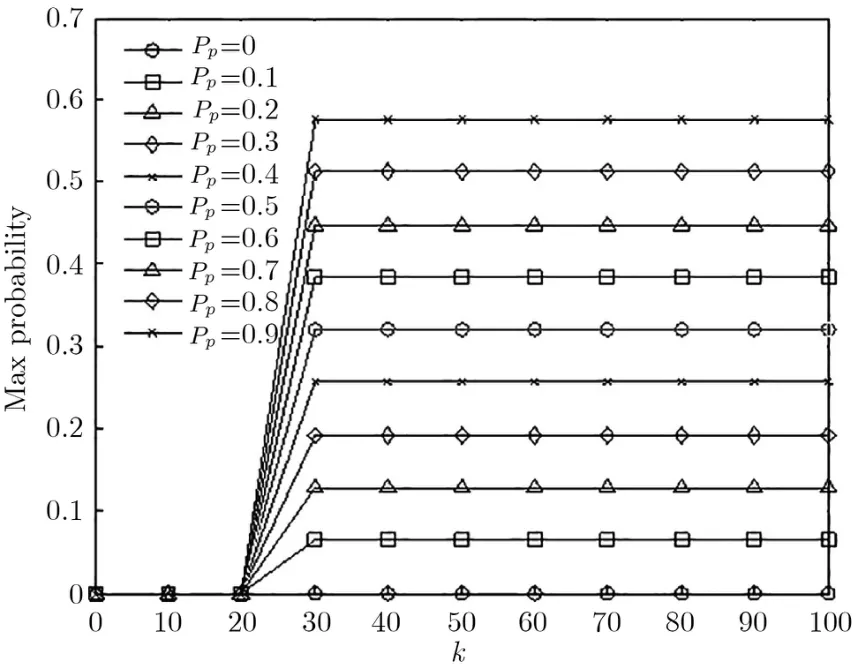
图4 到达状态Suni的最大概率Figure 4 Maximum probability when reaching state Suni

5 结束语

区块链技术是一种全新的分布式基础架构与计算方式,它主要利用块链式数据结构验证和存储数据,通过分布式节点之间的共识算法产生和更新数据.同时为了保证数据传输和访问的安全性,还引入了密码学技术.另外,区块链还利用由自动化脚本代码组成的智能合约来编程和操作数据.区块链技术的去中心化的特性引起了各行业的广泛关注,其中的激励机制设计是区块链技术的瓶颈问题.本文探讨了博弈论与区块链的交叉研究现状,分析了博弈论在比特币的激励机制设计中的若干问题.讨论了智能合约中内部和外部的安全隐患,并应用智能合约解决了可验证云计算问题,利用博弈论的思想,为云计算中的委托人设计了抗合谋的智能合约.最后还通过引入随机参数的方法,验证犯罪智能合约的有效性,降低了犯罪智能合约成功的概率.区块链技术方兴未艾,区块链3.0,其中包括:区块链自洽组织(DAO)、区块链自洽公司(DAC),是今后的发展方向.如何利用博弈论设计更加合理的激励机制仍然是区块链与博弈论交叉学科的研究热点.另外,区块链在大社会中的应用,例如,科学领域,医疗领域,教育领域等,也为区块链技术产业化提供了更多的发展契机.