基于旅客计划延误的航班频率优化研究*

姜思露 朱金福 孔明星 周秦炎

(南京航空航天大学民航学院 南京 211106)

0 引 言

航班计划是航空公司一切生产运营活动的基础和核心，对航空公司的经营状况与市场竞争力起着决定性作用.航班计划的编制步骤环环相扣，紧密联系，航班频率的确定作为其中的关键环节，对航空公司的生产运营有着深刻影响.而旅客计划延误是旅客选择航空公司和航班的重要依据之一，在考虑旅客计划延误的前提下进行航班频率的优化研究对旅客和航空公司都具有重要意义.

国外关于旅客计划延误和航班频率的相关研究始于20世纪70年代，Douglas等[1-2]提出了“计划延误(ScD：ScheduleDelay)”和“随机延误(StD：Stochastic Delay)”的概念.Chang[3]以旅客计划延误成本最小，研究了航班时刻待定情况下1 d的航班频率和航班时刻.Hsu等[4]应用模糊逻辑理论研究了航空公司之间航班频率和平均票价的竞争关系.Bao等[5]提出了一种针对多机场系统的航班时刻和航班频率优化模型.Abdelghany等[6]提出了一种竞争环境下的航空公司航班计划建模框架.

国内较为代表性的研究有：朱金福[7]建立了利润最大化的航班频率优化模型；朱星辉[8]基于航空运量预测对航班频率进行了研究.国内其他针对航班频率的研究大多只讨论了单机型情况下的优化，数学模型较为简单，难以在实际运用过程中为航空公司提供决策支持.相对于国外在航班计划、航班频率优化和旅客计划延误方面丰富的研究成果，显然国内在这几个方面的研究还不够全面和系统.本文的研究目标是在综合考量旅客计划延误和航班运营成本的基础之上，根据航空公司实际需要引入约束条件，解决航班频率优化建模问题，提出一种航班计划优化方法，旨在为航空公司航班计划编制提供理论支持和决策参考，最终实现降低航空公司运营成本的目的.

1 航班频率优化问题概述

航班计划是在市场分析和预测的基础之上，对航空公司有限的资源(飞机、航线时刻、人力、资金等)进行科学分配，从而确定正班飞行的航线、频率、时刻、机型和执飞的飞机、机组[9].航班频率，又称航班班次或航班架次，是指航空公司在一定周期内(可能是1 d、1周、1个月乃至1个季度等等)在各条航线市场上的航班量.航班频率的优化和确定是航空公司制定航班计划的核心环节，涉及航线需求，可用机型，运力供给，竞争对手市场占有率等方面，对航空公司的生产运营有着深刻影响.只有确定了各条航线的航班频率，才能进一步对时刻和机型进行分配，从而完成航班计划的编制.

为了将航班频率的确定量化考虑，本文假设航班计划周期为1周，在已知航线需求的基础上介绍旅客计划延误计算公式，进而对航班频率进行优化.最小化旅客计划延误时间，等价于最小化旅客计划延误成本，其本质是最大化需求获取.而对于民航运输企业来说，旅客需求的增长意味着运营收入和市场占有率的上升，进而意味着航空公司市场竞争力的提升.因此，以旅客计划延误成本作为目标函数的主要组成部分进行航班频率优化具有重要的研究价值.

2 航班频率优化建模

在航班频率方面，国内相关研究大多只讨论了单机型情况下的优化，对拥有多机型的航空公司来说实用性不佳.国内最具参考价值的研究是文献[7]以利润最大化为目标函数建立的多机型多航线航班频率优化模型，该模型考虑了旅客需求、运力供给和航班频率整数约束.与该利润最大化模型不同，本文模型以旅客计划延误和航班运营成本之和最小为目标函数，除了旅客需求约束和运力供给约束外，还考虑了飞机最低利用率约束和航线容量约束，并将市场竞争因素纳入其中.

2.1 成本分析

所谓的旅客计划延误是指旅客计划的(期望的)出行时间与可供旅客选择的最近一班航班的计划离港时间之间的间隔.例如，某旅客计划出行的时间为10:00，而在该航线市场上与这个时间相隔最近的航班是10:30，那么对于该旅客来说，其计划延误时间为30 min.如果假设该旅客计划延误的单位成本为80元/h，那么该旅客的延误成本为40元.

为了降低计算难度，假设一个航班计划周期(1周)内，旅客需求在每天的运营时间段平均分布，例如，航空公司每天的运营时间段从06:30—22:30，则在每天的这16 h内旅客需求平均分布，且在1周运营的112 h内旅客需求平均分布.由于本文的研究对象是从总需求角度计算旅客计划延误和确定航班频率，而没有进一步考虑航班时刻的确定，所以在保证总需求等价的情况下，旅客需求在运营时间段内是否均匀分布不影响旅客计划延误计算和航班频率优化结果.为使旅客计划延误计算公式意义明确，进一步作出以下假设：①旅客的计划出行时间是一个确定的时刻；②旅客乘坐航班时，会选择离计划出行时间最近的航班.

文献[4]给出了基于Simpson分担率公式的旅客计划延误时间计算公式.取β=1，针对市场分担率公式考虑多种机型，即以本航空公司的航班座位数为标准，根据座位数对航线上其他航空公司的航班频率进行标准化处理，再乘以平均每旅客计划延误时间，可得本航空公司在所有运营航线上的总旅客计划延误时间.

(1)

式中:l∈{1,2,…,L}为航线市场；a∈{1,2,…,m,…,A}为运营同一航线市场(参与竞争)的所有航空公司；m为本航空公司；Rlm为本航空公司在航线市场l上的旅客需求，平均每位旅客的计划延误时间Sdlm等于航班时间间隔的1/4；T为一个航班计划周期内的总运营时长；Rl为航线市场l上的总旅客需求；Fla为a公司在航线市场l上的航班频率.

由式(1)可知，若直接将最小化旅客计划延误作为目标函数优化航班频率，优化所得的航班频率等于航空公司总运力允许的最大值.但这样的结果显然不符合实际需要，因为航空公司不可能只考虑旅客需求来安排航班，为了达到成本最小化的目的，航空公司还需要考虑运营过程中其他的成本因素.

为了使建立的航班频率优化模型更具有实用性，本文考虑两种成本：①从旅客角度出发考虑旅客计划延误成本，用平均单位延误成本与计划延误时间相乘后代入模型进行计算；②从航空公司角度出发考虑航班运营成本，根据航空公司历史数据，计算各航线平均每架次航班运营成本代入模型进行计算.

2.2 多机型多航线竞争环境下的航班频率优化建模

基于前文讨论的旅客计划延误计算公式，建立多机型多航线竞争环境下的航班频率优化模型.本文模型以最小化总成本为目标函数，总成本等于旅客计划延误成本和航班运营成本之和.国内外已有的航班频率模型多以利润最大为目标函数，或以运营成本最小为目标函数，运用线性整数规划法进行优化.也有以旅客计划延误最小为目标函数的相关研究，模型虽然是非线性的，但能使用拉格朗日松弛等方法转化为线性整数规划模型进行求解.目前，还没有同时考虑航班运营成本和旅客计划延误成本的研究，其原因在于同时考虑这两种成本时，模型是非线性的且难以转化为线性模型，进而导致求解的难度大幅度提高.而本文建立的模型为兼顾旅客和航空公司利益，同时考虑了两种成本，在后续的运算过程中讨论了求解方案，所得结果对航空公司来说更具有参考价值.

在研究航班频率优化的约束条件时，本文在总结常用约束的基础之上，进一步根据航空公司的实际需要，引入了新的约束.国内外有代表性的航班频率模型通常考虑如下约束：旅客需求、运力供给、飞机流平衡、机场最大出发航班数等.本文在此基础之上，一方面考虑满足所有航线上的旅客需求，即不允许旅客溢出，另一方面考虑优化得到的结果需要迎合航空公司的运力供给能力和对飞机使用经济性的要求，还需针对航线考虑最大容量约束[10].为此，模型考虑如下约束条件：旅客需求约束、运力供给约束、飞机最低日利用率约束、航线最大航班频率约束.由于研究对象是航空公司执飞的各条航线，所以不考虑飞机流平衡约束和机场最大出发航班数约束.新增的飞机最低日利用率和航线最大航班频率约束虽然进一步增加了模型求解的复杂度，但更符合航空公司运营实际情况，使模型更具有实用性.

为了将目标函数和约束条件表达为数学公式，首先定义模型的集合、参数和变量为：

①集合，L为航线集合，有l∈L；K为机型集合，有k∈K.②参数，cSD为旅客计划延误单位成本；cl为航班运营成本，即在航线l上每增开一个架次的航班所增加的成本；T为航班计划周期，h；Td为航班计划周期，d；Rl为一个航班计划周期内，航线l上的旅客需求；MSl为本公司在航线l上的市场分担率；ul为航线l上的平均客座率；sk为机型k的可供座位数；tlk为机型k执飞航线l的轮挡时间，用航线的轮挡距离除以机型的巡航速度求得；μk为机型k的最大日利用率；ηk为机型k的最小日利用率，若机型的日利用率低于该数值则认为优化所得到的结果是不经济的；nk为一个航班计划周期内，机型k的可用飞机架数；fl为一个航班计划周期内，航线l上允许的最大航班频率.③变量：Flk为航线l上机型k的航班频率；C为总成本，包括旅客计划延误成本和航班运营成本两部分.

综上所述，使用式(1)计算总旅客计划延误，则可建立如下数学模型

(2)

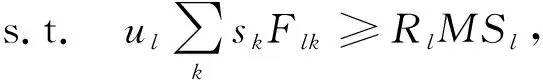
(3)

(4)

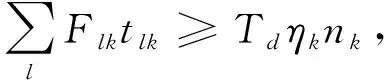
(5)

(6)

Flk≥0,∀l∈L,∀k∈K

(7)

式(2)为最小化总成本的目标函数；式(3)为旅客需求约束，保证航空公司提供的运力大于等于航线上的旅客需求；式(4)为运力供给约束，限制航班频率与轮挡时间的乘积不得大于航空公司所能提供的最大运力；式(5)为飞机日利用率约束，保证了各机型飞机的日利用率不小于最低水平，确保飞机使用的经济性；式(6)为航线容量约束，由于每条航线容量有限，不可能在航线上无限增开航班，因此，给出航班计划周期内航线上允许的最大航班频率来加以限制，以保证优化得到的航班频率不超过航线的容量；式(7)为航班频率取值约束，保证优化得到的航班频率不小于零.

2.3 模型求解分析

由于所建立的航班频率优化模型是非线性的规划模型，需要使用分支定界法求整数解，选用优化软件LINGO进行案例的计算求解.在进行小规模试运算时，发现全局最优求解程序花费的时间过长，程序运行4 h以上仍未得到最优整数解，因此考虑采用启发式算法求解.启发式算法是相对于最优化算法提出的，一个问题的最优算法求得该问题每个实例的最优解，启发式算法则定义为一个基于直观或经验构造的算法，在可接受的花费(指计算时间和空间)下给出待解决组合优化问题每个实例的一个可行解.对于航空公司来说，只有首先确定了各条航线的航班频率，才能进一步对时刻和机型进行分配，从而完成航班计划的编制.因此严格控制运算时间，在较短时间内得到具有参考价值的航班频率优化结果，才能迎合航空公司的实际应用需要.本文在LINGO软件全局最优求解程序运行30 min时人为终止求解，得到实例的可行解.

在航空公司利用优化模型制定航班计划的过程中，可能会根据实际运营情况事先确定某条甚至多条航线的航班频率，即模型的部分变量等于固定值；也可能进一步考虑旅客溢出等情况，增加对变量的约束.在这种情况下，由于可行域范围缩小，运行求解花费的时间将会相应缩短，可以考虑选用最优化算法求得模型的最优解.

3 案例计算

某航空公司经营10条航线，各航线市场的航线长度、旅客需求、航线容量、客座率、市场分担率和平均每架次航班运营成本见表1.表1中，航线长度指航线的轮挡距离，航线容量指航线一周内允许的最大航班频率，航线需求、客座率和市场分担率是根据历史数据预测得出的该航空公司2017年某1周的航线需求、客座率和市场分担率，各航线平均每架次航班运营成本根据航空公司运营历史数据计算得到.该公司使用B737-300、B737-800和B767-300三种机型，分别标号为1，2和3并给出相关参数见表2.用航线的轮挡距离除以机型的最经济巡航速度，保留两位小数，只入不舍，可得各机型执飞各航线的轮挡时间见表3.该航空公司航班计划周期为1周，每天的运营时间段从06:30—22:30共计16 h，则T为112 h，Td为7 d.根据经验估算，平均每位旅客计划延误时间的单位成本cSD为60元/h.

表1 航线参数

表2 机型参数

使用案例中的参数和数据，利用LINGO软件对航班频率优化模型求解，在运行30 min时人为终止求解，得到的结果见表4，总成本C为6 142 621元.此时目标函数的下界值(Objective Bound=6 122 705)与目前得到的最好的可行解的目标函数值(Objective Value=6 142 621)相差的值已经在可接受的范围内，可以认为已经得到了全局较优解.

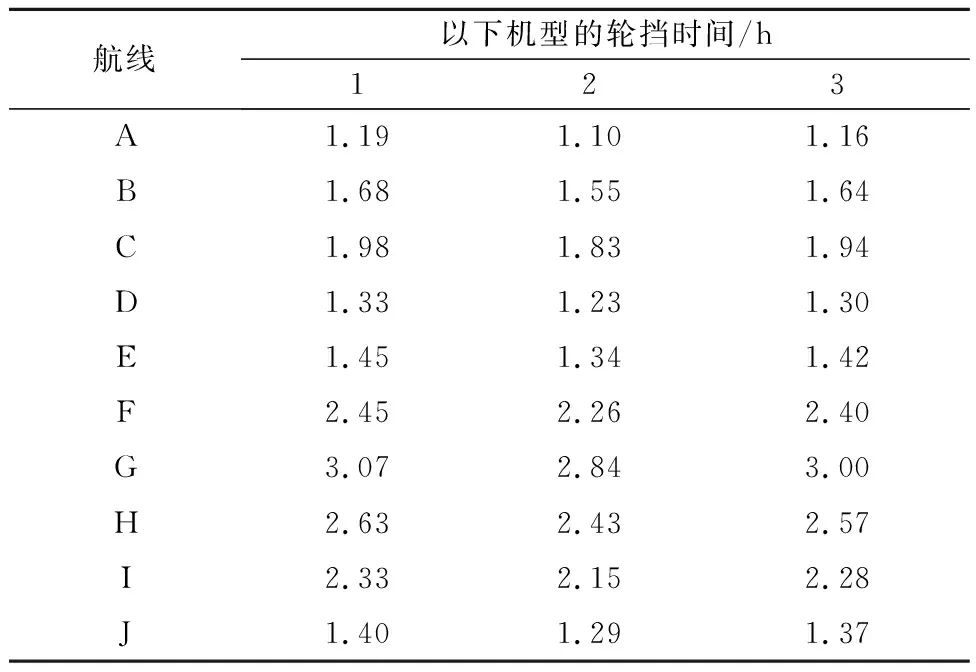
表3 各机型执飞航线的轮挡时间

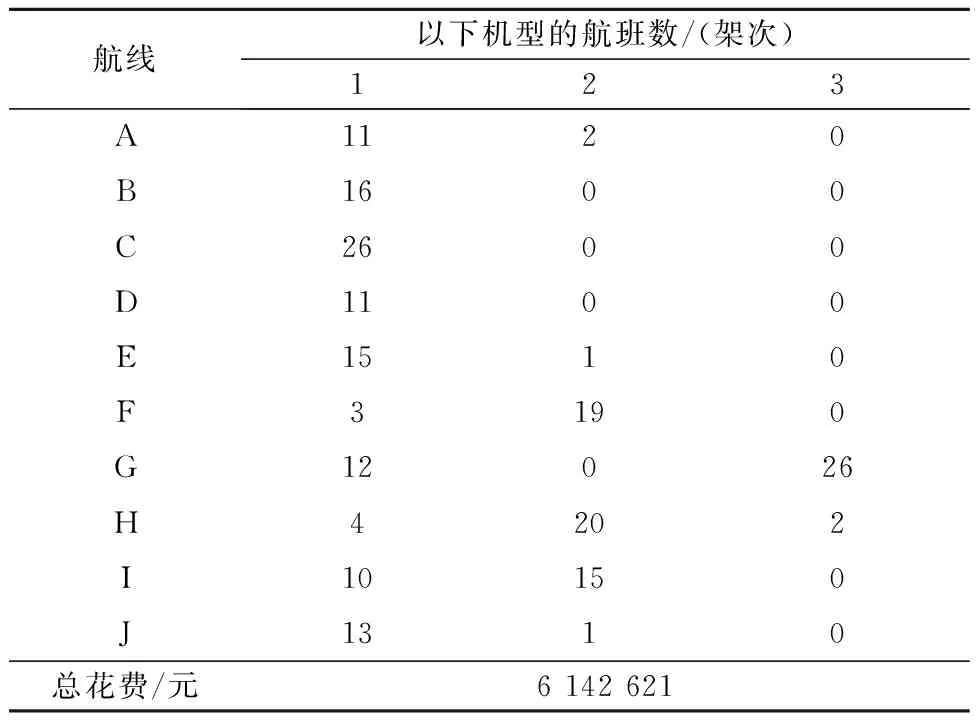
表4 软件优化结果

上述案例计算证明，本文建立的航班频率优化模型不仅同时考虑了旅客计划延误和航班运营成本，而且具有较好的可行性和实用性，能在航班频率优化方面为航空公司提供参考.

4 结 束 语

合理地编制航班计划能为航空公司节约运营成本，并且在很大程度上提高航空公司的运营管理效率，从而提高收益.本文针对航空公司航班计划的编制与优化，研究了旅客计划延误计算和航班频率优化，建立了多机型多航线竞争环境下的航班频优化模型，提出了一种航班计划优化方法.通过案例计算，运用优化软件LINGO对模型进行了求解，验证了模型的效用.优化结果表明，本文所建立的模型能为航空公司航班计划编制提供理论支持和决策参考，在一定程度上降低航空公司的运营成本.