基于VAT的信号交叉口危险变道行为风险特性分析*
2019-03-01郝艳萍徐良杰王啸啸
郝艳萍 徐良杰* 王啸啸
(武汉理工大学交通学院1) 武汉 430063) (河南城建学院土木与交通工程学院2) 平顶山 467036)
0 引 言
信号交叉口危险变道行为易引发交通事故.相关统计结果表明,车辆换道产生的碰撞事故占总碰撞事故的4% ~10%,多是由于驾驶人对目标车道前后车辆车头时距判断失误,进而诱发交通事故[1].
目前,国内外学者在危险变道行为方面的研究主要集中在危险变道行为的影响因素及基本特性[2-3]、对交通流及交通安全的影响等[4],通过行车轨迹建立不同的数学模型,对危险变道行为进行分析及判定[5-6].针对信号交叉口危险变道行为风险特性分析方面的研究较少.对于碰撞时间(TTC)模型的研究,则主要集中于跟驰车辆的交通冲突[7],缺乏对于变道行为冲突的研究.
文中提出了风险特性参数车辆接近时间(VAT)模型,利用Lasso-LARS算法对数据集进行训练,确定车辆接近时间(VAT)与各自变量之间的相关性系数,通过算例分析验证了VAT模型的准确性.
1 危险变道行为界定
在信号交叉口上游路段、渐变段进行变道属于正常变道,车辆在进入信号交叉口实线段后进行变道属于违章变道行为,见图1.
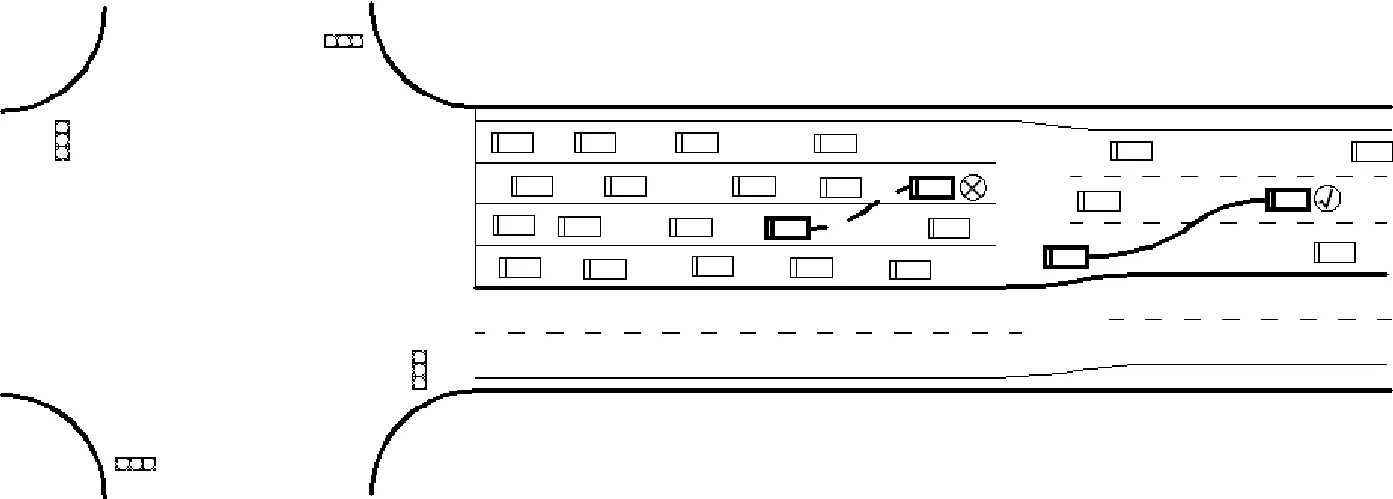
图1 允许和禁止变道范围图
违章变道对交通流影响较大,容易引发交通事故.除此之外,非实线段驾驶员的变道行为也可能会对近信号交叉口路段及信号交叉口功能区车辆通行的正常秩序和行车安全造成影响.因此,本文界定的危险变道行为根据危险变道行为发生的位置分为两大类:实线段危险变道、非实线段危险变道.
车道变换行为的多样性决定了危险变道行为的多样性,根据危险变道行为发生时车辆的行驶轨迹,将每一类危险变道行为进行划分,实线段危险变道行为分为强制变道、随意穿插变道、未成功变道三类,非实线段危险变道分为强制变道、随意穿插变道、连续变道三类.
2 危险变道行为风险特性参数建模
2.1 数据采集
本研究选择武汉市青山区友谊大道的两个信号交叉口进行交通调查.调查时段为2018年3月1—3日早晚高峰(07:30-09:00;17:00-18:30)及平峰(09:00-10:30;14:30-17:00)的代表时段.调查数据统计见表1.
2.2 数据预处理
对采集到的危险变道车辆行车数据进行分析,具体见表2.

表1 危险变道调查数据样本统计
注:1-友谊大道到工业路;2-友谊大道到建设一路.Q-交通量,pcu;R-危险变道数量,pcu.
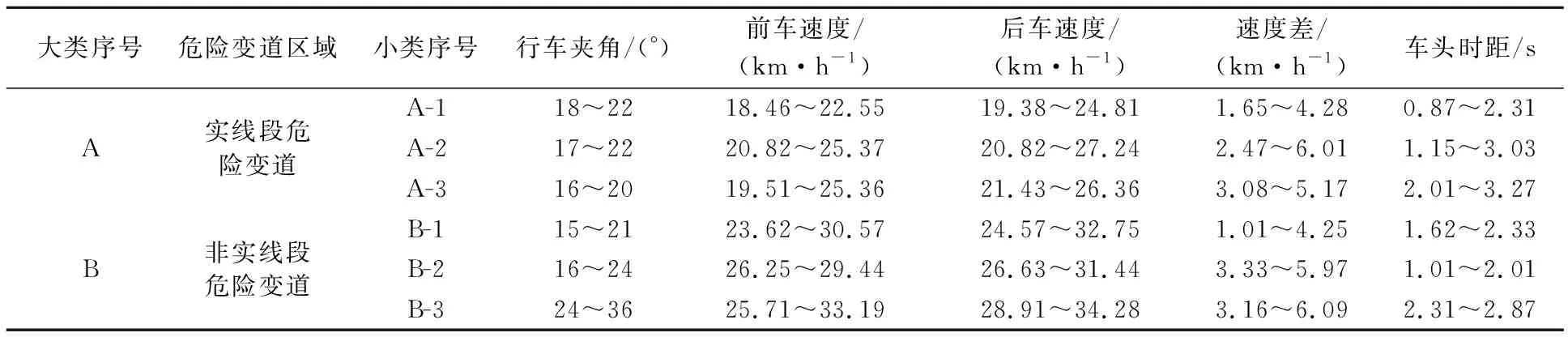
表2 危险变道行为交通参数统计
如表2统计所得危险变道行为发生时该进口道交通参数,不同参数之间存在不同程度的交叉,无法具体分析各类危险变道行为的风险特性,故考虑建立车辆接近时间(VAT)模型对其风险特性进行分析.
道路交通系统的运行状态受到人、车、路和环境的影响不断发生变化,危险变道行为也是如此.由于调查手段及调查结果的制约,同时考虑到不影响交叉口处车辆的正常通行,故本研究中不考虑驾驶人因素,本文涉及的影响因素包括:变道行为发生的时间、变道车辆的车型、转向角、变道持续时长、原车道及目标车道前后车的车速及车头时距等因素.
2.3 车辆接近时间(VAT)模型
本研究将VAT定义为在信号交叉口危险变道行为中,当目标车辆变道至目标车道,若前车(目标车)速度小于目标车(后车)速度,前后两车距离较小而产生交通冲突,目标车(后车)未采取制动措施,则两车会发生碰撞,从产生交通冲突到碰撞的时间称为车辆接近时间.基本原理见图2.

图2 车辆接近时间(VAT)模型图
传统TTC模型适用于跟驰车辆碰撞时间的计算,不可直接用于危险变道行为风险特性的评价,考虑加入转向角θ变量以提出VAT模型,具体计算公式为

(1)
式中:VATi为第i辆车与前车(i+1车)或后车(i-1车)的车辆接近时间,s;xi(t)为第i车在道路上的位置,m;vi(t)为第i车从危险变道行为发生至可能发生碰撞的行程车速,m/s;θi为第i车(目标车辆)的转向角,(°);li为前车的车长,m.
车头时距与车头间距的关系为
di=xi(t)-xi-1(t)=vi-1·hi-1
或di=xi+1(t)-xi(t)=vi·hi
(2)
式中:di为车头间距,m;hi为第i+1车与第i车之间的车头时距(t).
故式(1)可以表示为
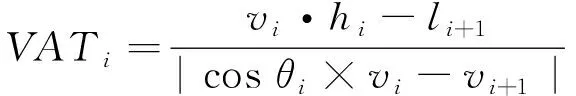
(3)
实地调查和视频观测时发现,若目标车辆采取变道行为,则目标车道后车会及时采取制动措施,使用VAT模型时需考虑驾驶人反应时间.若计算所得VAT值小于目标车道后车驾驶人反应时间,则可直接根据式(3)进行计算;若计算所得VAT值大于目标车道后车驾驶人反应时间,则需要根据后车制动后的速度及车头时距进行计算.在此处计算时需考虑前后两车的车速及加速度,所以在计算模型中采用平均车速进行计算,而非瞬时速度,提高模型的准确性.基于计算所得的VAT值,可分析得到不同危险变道行为的危险程度,VAT值越小,表示车辆接近时间越小,即发生碰撞的可能性越大,危险程度越高;反之则危险程度较低.
3 基于lasso-LARS算法的危险变道行为风险特性分析
3.1 变量标准化
利用Lasso-LARS算法对数据集进行训练,确定各因素的相关性系数.利用友谊大道-工业路交叉口处调查数据基于Lasso-LARS(最小角回归)算法训练数据.预处理后每组数据包含10项自变量及1项因变量.自变量中包含数值变量和分类变量,具体描述见表3.因变量为利用碰撞时间模型计算所得的车辆接近时间(数值变量),用向量Y表示.

表3 自变量变量描述
3.2 Lasso-LARS算法
考虑到危险变道行为发生时相关影响因素较多,使用Lasso-LARS算法[8]可对其不同因素的相关度进行拟合和求解,对于高维特征问题:
Y=Xθ
(4)
式中:Y为m×1的向量;X为m×n的矩阵;θ为n×1的向量;m为样本数量;n为特征维度.
把矩阵X看做n个m×1的向量Xi(i=1,2,…,m),在Y的X变量Xi(i=1,2,…,m)中,选择和目标Y最为接近(余弦距离最大)的变量Xk,用Xk来逼近Y,则:
(5)
(6)

定义自变量矩阵为
(i=1,2,…,270;j=1,2,…,10)
(7)
Y是对应的因变量的集合,求解Lasso-LARS问题公式为
Yij=θ1xi1+θ2xi2+…+θjxij
(i=1,2,…,270;j=1,2,…,10)
(8)
式中:θj为系数.
3.3 训练结果分析
将自变量向量X及因变量Y代入3.1中算法,通过R语言编辑并调整参数,基于Lasso-LARS算法得到模型训练结果(见图3),及自变量和因变量的相关系数矩阵,见式(9).

图3 模型训练结果
由图3模型训练结果观察,从左往右分析,每条折线表示每个变量的系数的变化情况,带数字的竖线表示变量加入的步骤.可以看到有些折线在左端时系数都是0,到达某一条竖线时系数开始变化,表明系数加入.不同的变量对危险变道行为VAT的影响程度不同,各变量相关性系数矩阵为
θT=
[0 5.569 663×10-26.983 032×10-5
1.948 074×10-18.637 113×10-1
2.103 403×10-13.903 212×10-1
9.738 479×10-27.713 337×10-1
8.381 305×10-2]
(9)
根据训练结果及相关性系数矩阵可以看出,不同变量的相关性系数不同.根据式(9)中相关性系数矩阵,将θj代入式(8)即可求得各变道行为的VAT.
4 案例验证
4.1 友谊大道-建设一路交叉口数据
信号交叉口的危险变道行为在不同VAT取值范围内发生的频率有显著差异,采用视频调查中20个信号周期的调查数据进行分析,初步统计结果见图4.
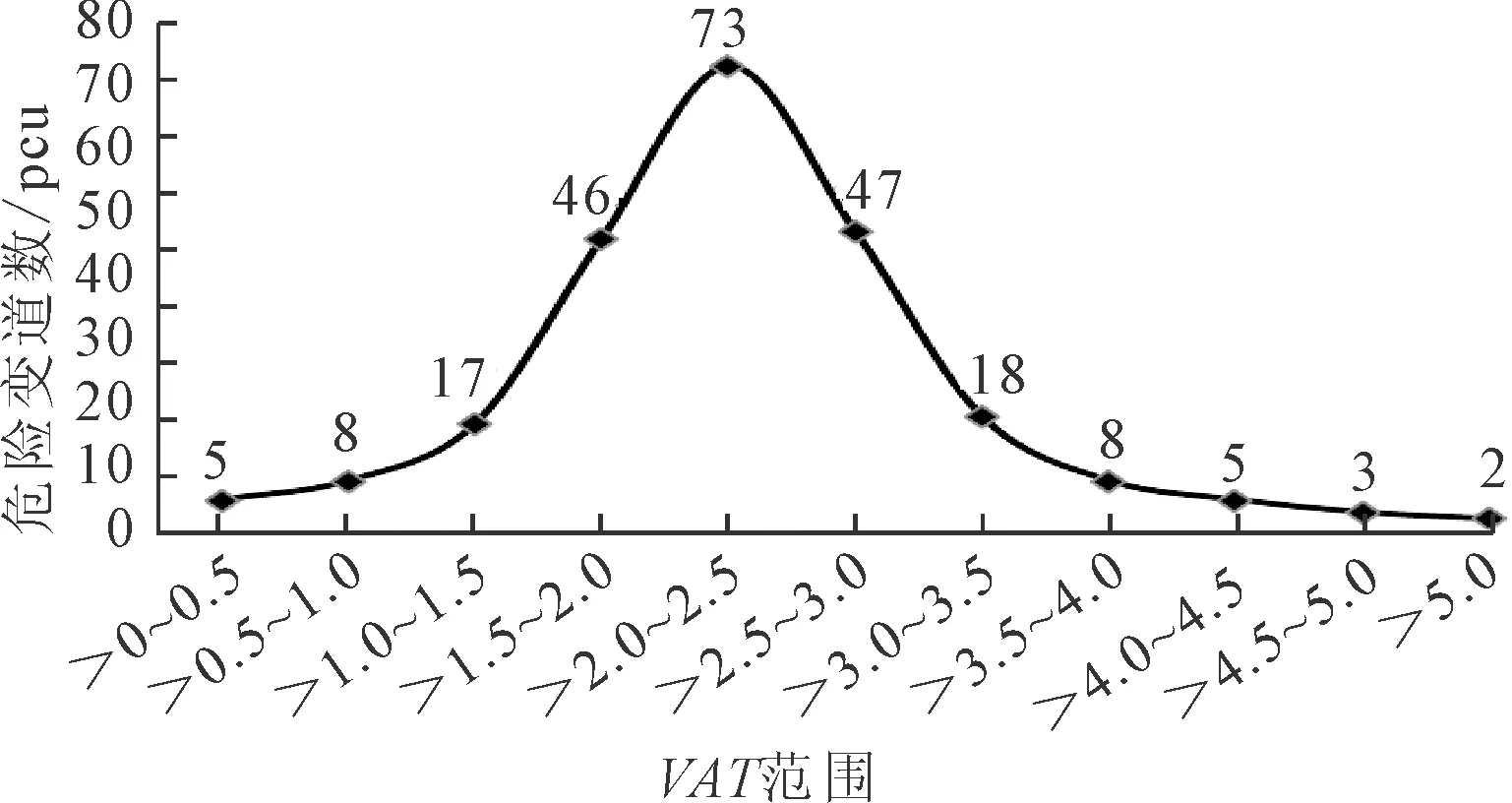
图4 不同VAT范围内危险变道行为频率分布
由图4观察可知,危险变道行为在VAT范围的分布频数先上升后下降,危险变道行为在VAT范围的分布频数先上升后下降,使用MATLAB数据分析软件对数据进行正态分布拟合,发现VAT曲线服从置信度为0.95的正态分布,在VAT为2.5 s左右时,危险变道行为发生的频率最高;根据美国各州公路工作者协会推荐,驾驶人风险判断时间为1.5 s,行为时间为1 s,故本研究以VAT=2.5 s为界定标准,对危险变道行为进行分析研究.
郝艳萍危险变道行为一般分为三个阶段:判断-决策-操作.部分驾驶人会忽视交通环境进行变道操作,导致危险变道行为的VAT较小.当VAT<2.5 s时,危险变道行为发生的频率高达64.22%;VAT>2.5 s时,发生频率为35.78%,由于变道过程中驾驶人及时作出反应操作,均未出现交通事故.
4.2 不同类型危险变道风险分析
根据1中对危险变道行为的分类,对友谊大道-建设一路信号交叉口危险变道行为统计分析,见表4.
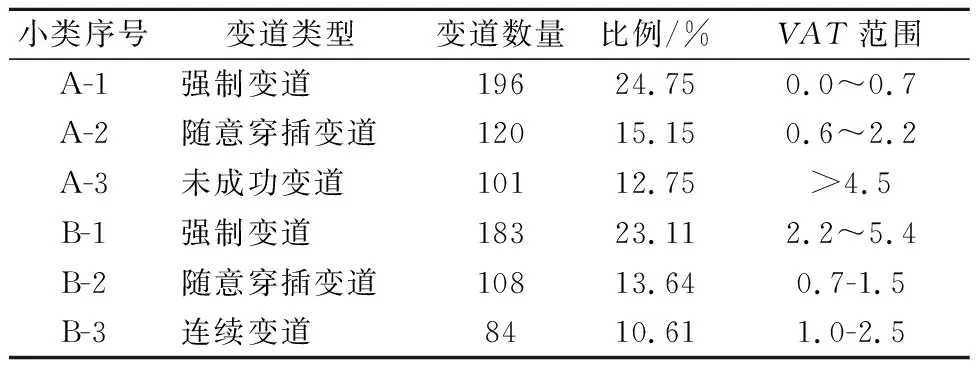
表4 不同类型危险变道行为分布情况
由表4可知,不同危险变道行为危险程度不同,进一步分析得出以下结论:①信号交叉口危险变道行为多发生在信号交叉口进口道实线段,占危险变道总数的52.65%,同时实线段危险变道行为危险程度也较高,这是由于信号交叉口渐变段距离较短或交通标志边线设计不合理,导致驾驶人反应时间不足;②强制变道占危险变道行为总数的47.85%,这是由于信号交叉口交通环境复杂,变道需求较大,其中实线段强制变道行为危险度最高;③有28.79%的选择在信号交叉口随意穿插变道,驾驶人为追求自由行驶速度而随意变道,其中渐变段危险程度更大,这是由于在渐变段驾驶人行车速度较大,较为危险;④连续变道行为在非实线段进行变道,当信号交叉口交通流较大或其后跟驰车辆速度较大时,连续变道较为危险.
4.3 结果分析
由3中模型训练及结果,根据相关性系数式(9)及式(8)计算可得危险变道行为的VAT值.利用SPSS统计分析软件,将危险变道行为的VAT模型计算值与Lasso-LARS算法计算值做配对T检验,置信度为95%,检验结果见表6~7.
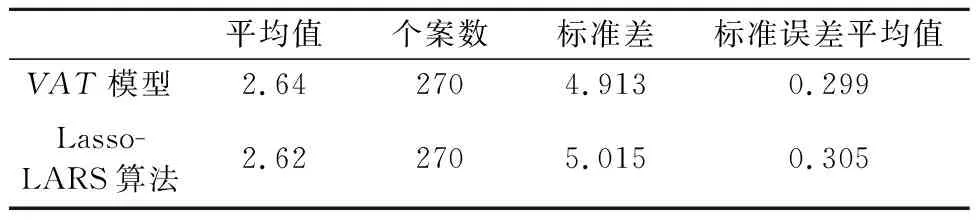
表5 配对样本统计
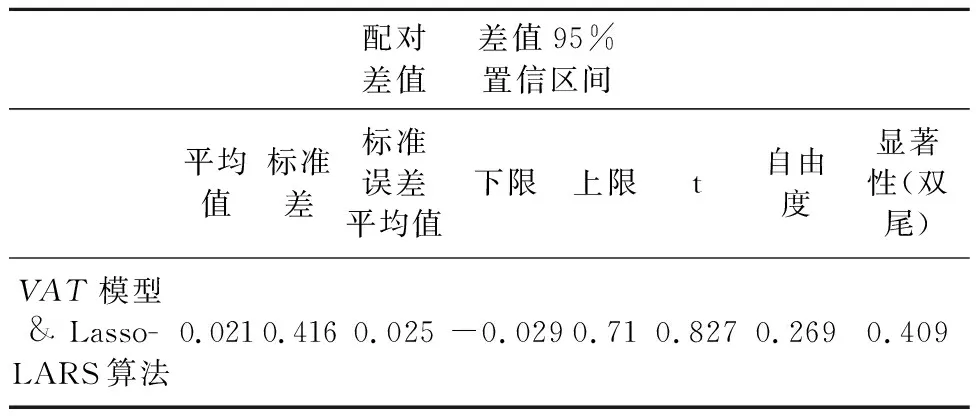
表6 配对样本检验
由检验结果分析知,VAT计算值与观测值在95%的置信度,两者结果基本吻合,说明了VAT模型的适用性及有效性.
5 结 束 语
针对信号交叉口危险变道行为进行调查及风险程度的研究,构建了描述变道行为的VAT模型,通过Lasso-LARS回归分析得到的VAT计算值对比分析发现,在95%置信区间范围内,二者不存在显著差异,验证了改进VAT模型的准确性.研究成果可为信号交叉口危险变道行为的安全性分析提供理论支撑.
