FPSO防护圆管在碰撞载荷下的变形研究*

2019-03-01刘清扬孔杰灵陈明胜

武汉理工大学学报（交通科学与工程版） 2019年1期

刘清扬朱凌孔杰灵陈明胜

(武汉理工大学交通学院1) 武汉 430063) (高新船舶与深海开发装备协同创新中心2) 武汉 430063)

0 引言

圆管在海洋工程中的应用十分广泛，如海底管道、海洋平台的支柱以及防护结构等.在一些大型的浮式平台如FPSO上，会配置有防止碰撞的圆管结构.当发生碰撞时圆管首先与撞击物接触以保护平台设备，这类防护圆管的直径与厚度的比通常在20～40[1].圆管受到撞击作用产生的变形不能过大，否则会影响设备的正常工作.而圆管的变形分为整体和局部变形，主要影响设备的是整体变形，因此，区分防护圆管的整体与局部变形显得尤为重要[2].

对圆管受到撞击产生的变形问题，大部分的研究都参考了Thomas等[3]对圆管三个变形阶段的定义.Jones等[4-5]通过系列实验研究了钢制圆管在侧向撞击载荷作用下的变形问题，并用壳理论对圆管的变形进行了理论分析.武勇忠等[6-7]采用实验和有限元相结合的方法对圆管的撞击进行了研究.雷建平等[8]进行了三组两端刚固的不锈钢焊管的撞击实验，给出了圆管局部变形与侧向载荷之间的关系.Jone等[9]对以往的实验进行了总结，并且提出了一种理想化的剖面用来从最终变形中分别计算出整体变形和局部变形，并对以往估算圆管受侧向冲击载荷产生最终变形的经验公式提出了一些改进建议.随着有限元商业软件的发展，很多动力学的问题都可以借助有限元软件来进行模拟.周丽军等[10]对自由圆管受平头弹体的冲击动力学行为进行了仿真，主要研究了圆管的变形时间历程、最终变形模态,以及能量的分配.Liu等[11]研究了球状冲头冲击有初始刻痕的梁的冲击响应，并用LS-DYNA得到了较好的有限元结果.杨庆丰等[12]对两端固支的圆管的抗侧向冲击性能进行了分析，讨论了径厚比、冲击角度、冲击速度等对冲击力和失效模式的影响.

近年来，圆管的撞击问题受到越来越多的关注.Travanca等[13]总结刚性体和变形体撞击变形体的问题，并给出了需要考虑的影响参数如管径、壁厚、应变率等等.Zhu等[14]对圆管受侧向冲问题进行了系列实验研究，重点关注了产生的整体与局部变形.Yu 等[15]专门对于海洋工程中的圆管受到船舶撞击的问题进行了综述.由此可见，圆管的撞击一直是研究的热点问题.而对于防护圆管，不仅需要对最终变形进行评估，整体和局部变形的区分也对保证设备的安全有重要意义.目前对于整体和局部变形的区分方法比较复杂，且存在很多理想化的假设.本文针对这一问题进行了一系列的研究.

1 圆管的实验研究过程

1.1 圆管尺寸与拉伸实验

实验按照钢制圆管尺寸的不同分为五组，分别用A～E编号表示，具体的尺寸参数见表1.

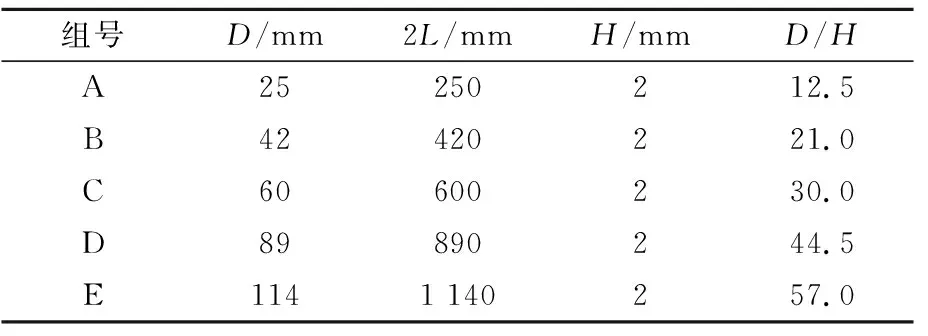
表1 实验圆管尺寸

注：D为直径；2L为管长；H为壁厚

钢制圆管的材料拉伸试样按照文献[16]规定选取.为了得到较为可靠的结果，对每组圆管分别切取四个试样在万能试验机上进行拉伸实验.根据式(1)可以将得到的工程应力-应变曲线转变为真实应力-应变曲线.

(1)

但式(1)仅在试样发生紧缩之前适用，紧缩之后通常会假设应力-应变符合指数关系[17]，为

(2)

式(2)系数的确定采用文献[18]的方法，分别表示为

n=ln(1+Ag)；C=Rm(e/n)n

(3)

式中：Ag为应力最大时对应的应变；Rm为最大的拉伸应力；e为自然对数底.

图1为D组圆管的工程应力-应变曲线和经过上述公式处理过后得到的真实应力-应变曲线.根据这一处理方法，依次汇总每组圆管的真实应力应变曲线，见图2.所得的材料曲线供后续实验结果分析和有限元中建立材料模型使用.

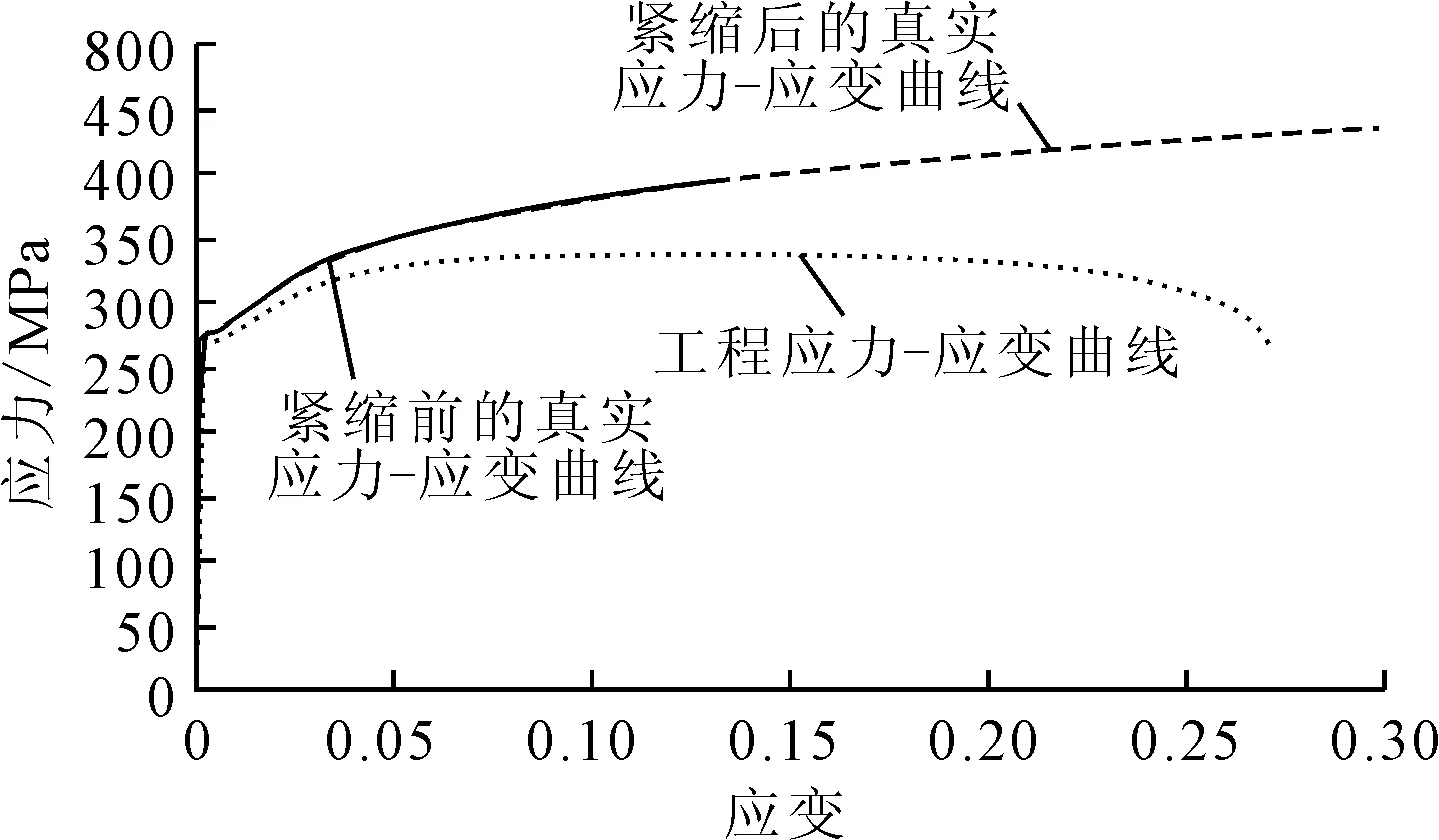
图1 D组圆管材料拉伸实验结果处理

图2 各组圆管真实应力应变曲线

1.2 圆管撞击实验

不同组圆管的系列实验在落锤冲击机上进行，其有效高度为2.7 m.落锤被安置滑轨上以保证竖直下落.落锤与起吊绳之间用电磁铁连接，起吊绳直径为10 mm.落锤冲击机的冲击速度完全依靠落锤自由落体产生.实验中使用GEN7t高速数据采集系统，采样频率选择 100 kS/s以保证在撞击瞬间记录足够数量的点.速度采用光电开关进行测量.本实验的撞击速度范围为2～6 m/s，撞击能量范围为60～1 400 J.冲头形状为楔形，端部宽度为2.5 mm，倾斜角度为15°.

实验采用自主设计的基座和夹具保证圆管两端刚性固定.在圆管两端钻孔并插入插销以限制圆管的轴向位移.径向位移采用垫片和夹具进行限制，固定不同管径的圆管时采用不同厚度的垫片.

实验圆管共约100根，去除重复实验及无效实验，有效实验圆管共68根.本文中主要关注圆管受到撞击后产生的变形.A组的变形圆管见图3，在撞击能量较小时圆管的局部变形明显；撞击能量较大时圆管的整体变形变得显著，整体变形与局部变形相互耦合.有关实验设备和过程的具体细节，可以参考文献[17].

图3 A组受撞击后的圆管

2 圆管的实验结果分析

2.1 上下表面撞击处的最终变形

实验中测量得到各组圆管管在不同冲击能量下的上下表面冲击处最终变形见图4.

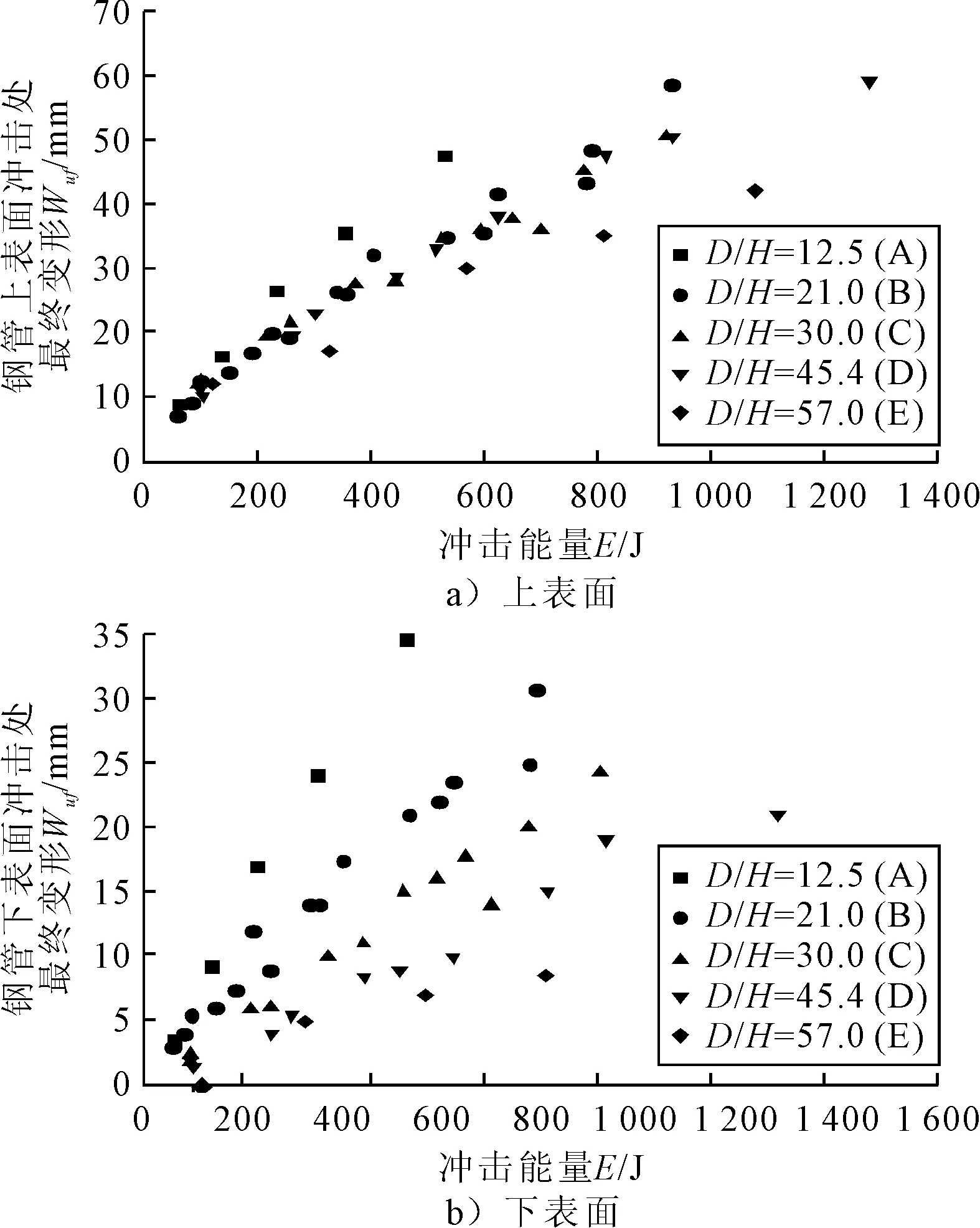
图4 各组圆管上下表面撞击处的最终变形

不同组的圆管用D/H这一参数区分，D/H的大小可以反应圆管具有薄壁还是厚壁的特性.由此可以得到D/H对上下表面最终变形的影响.由图4可知，D/H对于上表面最终变形和下表面最终变形的影响大小不同.不同D/H的圆管在一定的撞击能量范围内上表面最终变形仅略微发散，而下表面最终变形因D/H的不同而呈完全的发散状.这表明在相同的撞击能量下，D/H对于上表面变形影响较小，对于下表面变形影响较大.这为在相同的撞击能量下D/H较小的圆管局部变形不明显，而D/H较大的圆管局部效应明显这一现象提供了比较合理的解释.

进一步分析，D/H通过对圆管上下表面影响的不同而最终影响整体与局部变形的相对大小.这种对上下表面的影响不可能相同，否则无法体现圆管整体变形与局部变形耦合的特性.基于这一特点，可以借助撞击处上下表面最终变形的大小来定性反映整体与局部变形占最终变形的比重.仅测量两个点的最终变形较分析整个圆管的变形情况要更加简单.

2.2 整体与局部变形的区分

实验中还有一个现象需要注意，即圆管受到撞击后会出现下表面上移的现象.因为下表面会上移，所以上表面最终变形是整体变形Wg与上表面局部变形Wul之和，而下表面最终变形是整体变形Wg与下表面局部变形Wll之差，即

(5)

由于整体变形是圆管绕端部发生的转动，所以圆管的上下表面的整体变形是相同的.可得

Wuf-Wul=Wlf+Wll

(6)

即

Wlf/Wuf+(Wul+Wll)/Wuf=1

(7)

若Wlf/Wuf=0，即Wlf=0.则表示下表面不发生任何变形，这时Wul/Wuf=1，即上表面只发生局部变形，整个圆管上下表面均不发生整体变形，见图5a)，这也是Thomas等定义的圆管变形的第一阶段.

若Wlf/Wuf=1，即Wlf=Wuf，则上表面撞击处的最终变形等于下表面撞击处的最终变形.可以认为整个圆管是一根刚性很强的梁，这时Wul+Wll=0，而上下表面的局部变形不可能为负值，所以整个圆管上下表面均不发生局部变形，即Wul=Wll=0.这时圆管只发生整体变形，见图5b).但是对于本文所示的薄壁圆管来说，这种变形模式只是一种理想状况.

图5 圆管变形模式假设

由以上分析知，Wlf/Wuf的大小能够反映出圆管整体变形和局部变形的相对大小.通过Wlf/Wuf的值可以定性表征整体与局部变形占最终变形的比重.Wlf/Wuf越接近1，整体变形所占比重越大，Wlf/Wuf越接近0，局部变形比重越大.这一结论可以快速地对整体变形和局部变形进行分析而不必进行复杂的测量.

3 有限元分析与经验公式

3.1 有限元模型

对圆管撞击的有限元仿真采用软件ABAQUS/Explicit进行.圆管模型见图6，Z轴为圆管管长方向，Y轴为冲头下落方向.圆管冲击处为坐标面Y=0，Z=0.由于模型具有对称性，仅建立1/4的模型进行仿真，设置关于XY平面和YZ平面的对称边界条件，分析结束后可以显示完整模型的情况.

图6 有限元模型示意

圆管单元选择S4R三维可变形壳单元，经过验证网格大小取为2 mm时分析结果稳定.实验中的冲头接近于刚体，所以冲头的模型只建立与圆管表面接触的宽度为2.5 mm的矩形，采用解析刚体表征冲头性质.对冲头模型建立参考点，将冲头的质量和初速度都赋在参考点上.所有的几何参数均按照上文中实验的实际参数确定.冲头与圆管的接触设为面面接触，摩擦系数设置为0.15，圆管端部的边界条件为刚性固定.材料非线性通过在ABAQUS/Explicit中输入材料的应力-应变关系定义.各组圆管的材料模型按照1.1节中的结果，再将其变为塑性应力-应变输入.材料密度为7 850 kg/m3，弹性模量为206 GPa，泊松比为0.3.

3.2 有限元与实验结果对比

在对实验结果进行批量仿真之前，首先选择一组实验进行试算，将实验测量的加速度时程曲线与有限元中的结果进行比较，C13M组的结果见图7.

图7 C13M加速度时程曲线实验与有限元对比

实验结果和有限元结果基本吻合，实验曲线有一些高频信号造成的波动，可以通过滤波进行消除.实验的撞击结束时间较有限元的略长，可能是由于实验中的边界条件不能实现完全的刚性固定导致的.实验和有限元的加速度时程曲线与横坐标包围的面积基本相同，表明冲量基本一致.总体上，在ABAQUS中进行的有限元仿真能够较为真实的模拟圆管受到楔形体撞击的情况.

对各组实验圆管进行仿真，并将实验和有限元的结果汇总如下.图8为圆管上表面撞击处最终变形的有限元与实验结果的比较.各组圆管在不同撞击能量下的实验和有限元数据均吻合较好.撞击能量较大时，实验略高于有限元结果，但误差都在10%以内.考虑到实验中的不可控因素，认为能使用这些结果进行进一步的分析.

图8 实验与有限元结果对比

由图8可知，撞击能量较小时不同尺寸的各组圆管上表面最终变形差别不大.随着撞击能量不断增大，不同组圆管受D/H不同的影响开始显现.这一现象表明在一定的撞击能量范围内，不同组圆管的上表面最终变形符合相近的规律.结合对圆管受撞击后产生的变形模式分析，圆管在受到撞击后会首先产生局部变形，这一阶段是局部变形阶段；随着撞击能量的增大圆管将进入局部变形与整体变形耦合的阶段.在图8的能量范围内，由实验观察和有限元分析，圆管都仍处于局部与整体变形耦合的阶段.由此认为在一定的撞击能量范围内，各组圆管的局部变形可能具有相同的性质，而随D/H不同造成的差异则与整体变形关系较大.如果以上分析成立，那么不同尺寸圆管的局部变形可以用统一的经验公式进行计算.

3.3 经验公式拟合

根据实验和有限元的结果，若进行公式拟合还缺少关键的撞击能量较小的情况.为了使拟合的公式符合实际的物理意义，需要保证拟合曲线过零点.用有限元补充撞击能量较小的情况，设置冲头速度在0.2～2 m/s.

结合小冲击能量的特点，认为圆管圆截面二分之一高度的位置是可以表征整体变形的中性轴.从分析结果中输出冲击处截面的中性轴与管壁相交节点的最终位移表示圆管的整体变形，最终变形减整体变形就得到局部变形.中性轴是一个假设，认为中性轴将变形的圆截面分为周长相等的两部分.虽然这是一个理想化的假设，但是在小冲击能量下圆管局部变形较小无法影响到中性轴的位置时，得到的中性轴与管壁相交节点的位移可以近似认为是整体变形.这一方法在冲击能量较小的范围内能够得到较为准确的局部变形.将所得结果与实验结果进行汇总，结果见图9.

为了使经验公式更具一般性，采用无量纲化的结果进行拟合.撞击能量的无量纲化公式为

(8)

图9 各组圆管局部变形拟合

式中：σy为圆管的屈服应力；Ek为撞击能量.采用对数函数进行拟合，结果为

(9)

这一表达式足够简洁而且具有相当的准确度，其R2的值为0.96，这个值越接近1表示拟合的误差越小.另外，拟合的公式还具有较好的物理含义，当撞击能量为零时，局部变形为零.公式中量纲一的量化圆管局部变形与量纲一的量化撞击能量取对数后的倍数关系为0.1.此拟合的经验公式可以用于不同撞击能量下不同尺寸圆管的局部变形的计算.