温度和空隙率对沥青混合料疲劳断裂特性的影响*

蒯海东 薛金顺 高兴阳

(新疆交通建设集团有限公司1) 乌鲁木齐 830011) (长安大学公路学院2) 西安 710064) (新疆农业大学交通与物流工程学院3) 乌鲁木齐 830052)

0 引 言

重复交通荷载及低温应力引起的疲劳破坏是热拌沥青混凝土路面一个主要的早期破损形式.目前，最为传统的研究沥青混合料疲劳性能的方法是力学-经验方法.该法以材料的力学特性为基础，将轮载等输入因素与路面响应如应力、应变等输出因素联系起来.近几年，一些学者提出了连续损伤力学方法，该法能更合理地研究沥青混合料的疲劳行为[1].

这些常规的对沥青混合料疲劳特性的研究没有考虑在裂纹产生后，裂纹处产生的应力再分布.Jacobs等[2]提出可以采用断裂力学来研究沥青混合料的疲劳特性.但由于沥青混合物具有黏弹性，所以该研究存在一定的缺陷.针对沥青混合料独特的黏弹塑性，Song[3]提出了黏弹性内聚区的方法，以适当地考虑在较大的裂纹产生区域内沥青混合料的逐步软化和黏弹性特征.该文对沥青混凝土断裂特性进行了较为深入的研究，但是仅考虑了单调加载条件，而没有进一步探究在循环负载条件下沥青混合料的疲劳裂纹扩展情况.Schapery[4]曾经开发出一套基于广义J积分法，在重复加载条件下的沥青混合料疲劳裂纹扩展模型.在该模型的开发过程中，对三种沥青混合料进行了一系列实验室测试，施加了不同大小和频率的荷载.通过实验，笔者认为广义J积分是表征沥青混合料断裂行为的较为合适的参数，并最终建立了基本形式的疲劳裂纹扩展模型.

文中依据前述的基本形式的沥青混合料疲劳裂纹扩展模型，设置不同的温度和空隙率条件，对三种不同的沥青混合料进行了试验，获取了模型中相关参数的数值变化情况，进而研究了温度和空隙率与沥青混合料疲劳特性的关系.

1 基本模型

1.1 广义J积分法

在一定的条件下，可以通过应力强度因子K表征疲劳裂纹的生长特征.如果材料是线弹性的，比如，水泥混凝土，裂纹尖端的产生取决于当前的K值；此外，在重复荷载作用下，裂纹的生长速度可以通过如下的Paris-Erdogan法则为

(1)

ΔK=Kmax-Kmin

(2)

式中：Kmax，Kmin为每一次加载循环中K值的最大和最小值；a为裂缝长度；N为循环加载次数；C和m为—回归系数.

由于沥青混凝土是黏弹塑性材料，对温度有较强的温度敏感性，因此，相较于应力强度因子K，Schapery理论[5]中的J积分更适合用来描述在裂纹尖端处发生的裂纹扩展.用广义J积分表征在大屈服条件下沥青混凝土的裂纹扩展，表达式为

(3)

式中：D(t-τ) 为蠕变柔量；KⅠ为模式一中的应力强度因子；t为积分下限，定义为在塑性区刚达到裂纹扩展点的时间点；t0为积分上限，定义为塑性区穿透裂纹扩展点的时间点.

用广义积分J替代式(1)中的应力强度因子K，可得到沥青混合料这类黏弹性材料的疲劳公式为

(4)

式中：ΔJ 为式(3)中每个加载循环里积分J的最大值和最小值的差值；A和n为回归系数.

1.2 裂纹扩展模型

由1.1可见，Schapery理论本质上仍是沿用Paris公式，即用广义J积分理论发展了一个与Paris-Erdogan方程同样形式的裂纹扩展方程，但只是利用沥青材料的黏弹材料特性预测Paris公式中A和n两个材料参数值，进而分析沥青混合料在不同环境下的疲劳特性.

在笔者之前的工作中，应用不同大小和频率的荷载对三种沥青混合料进行了测试分析，并分别用Paris-Erdogan法则和广义J积分的公式对其中的参数C(A)和m(n)进行了回归分析.结果表明，传统的Paris-Erdogan法则中的ΔK能够考虑到混合物的荷载大小的依赖性，但不能考虑到荷载频率的依赖性；而ΔJ积分可以有效地考虑到荷载频率的依赖性.此外，式(4)中的回归系数A和n保持恒定.

2 试样制备和试验设计

2.1 试样制作

在实验室试验中制作了三种不同的沥青混合料，每种沥青混合料的材料组成见表1.

表1 不同类型沥青混合料的材料组成

首先将旋转压实的混合料切成了两个盘状的样本：直径为150 mm，厚度为(50±1) mm.再通过动态模量实验，选择间接拉伸模式，获得了每种沥青混合料的黏弹性参数.最后进行了疲劳裂纹扩展实验.在疲劳裂纹扩展试验中用水喷机械切割试样以形成装载孔，初始裂纹槽口和平边缘切口见图1.

图1 切割后的沥青混合料样品

2.2 试验设计

在间接拉伸动态模量试验中应用Kim等[6]提出的试验安装和分析程序.在七种不同的温度和四种不同的频率下进行了试验.基于时间-叠加原理，应用试验数据构造了动态模量主曲线.依据Park等[7]提出的相互转换过程，将动态模量值转换了蠕变柔量值.

最后，应用Prony级数对蠕变柔量主曲线进行了数学表达，表达式为

(5)

式中：D(t)为蠕变柔量对时间的函数；D0，Di为材料常数；τi为第i次弛豫时间.

在一个能控制温度在-20 ℃和40 ℃之间(误差在±0.1 ℃内)的环境室内，用MTS材料测试系统，进行了相关实验.荷载用10 kN测力传感器监测.

用Wagoner等[8]提出的装载夹具尺寸，以确保将试验所需的预期载荷正确地施加于样品上.荷载的具体施加形式采用了没有间歇时间的正弦波.疲劳裂纹扩展过程由两个数码相机监控.以1 min的间隔拍摄样品两侧的裂纹扩展情况(以JPG格式记录，分辨率为1 600×1 200像素).具体实验过程见图2.

图2 加载试验设备和相机

为了研究温度和空隙率对沥青混合料疲劳特性的影响.选取了五个不同的温度(-10，0，10，20和30 ℃).为了模拟现场条件，每种温度下还选择了三种不同的空隙率(小、中和大).

由于荷载条件如振幅和频率已经在笔者之前的工作研究过了，所以在实验中用10 Hz的恒定荷载频率.但是，为了节省时间，加快破裂过程，采用了不同的荷载振幅.因为J积分可以考虑到荷载振幅与裂纹扩展速度的相关性，所以如果保持其他实验条件不变，就可以在不同的荷载振幅条件下得到同样的J值.

每个实验持续进行，直到有一个主裂纹扩展完全穿过样品.应该注意到的是，要将样本的缺口进行(凹口长度为27.5 mm)预破裂直到初始裂纹长度达到30 mm以消除每个样本不同的切口尖端尺寸的影响.

3 试验结果与分析

参考文献[5]用式(3)中的蠕变柔量值和应力强度因子K值计算了J积分的值.计算沥青混合料疲劳断裂试验中每种温度下相应的蠕变柔量值.代入到式(4)中并进行了一系列的回归分析，进而确定回归系数A和n，结果总结见表2.

3.1 温度的相关性分析

为了研究温度对沥青混合料的裂纹扩展影响，结合前述的疲劳扩展模型分析温度变化(-10～30 ℃)对沥青混合料断裂影响.

将3种样品均设定为标准的空隙率，考察它们分别在不同温度下的裂纹扩展情况,因此，以温度为横坐标，参考A值(AR)为纵坐标，得到了图3所示的折线图.

图3 AR与温度的关系

样品号温度/℃空隙率/%ARAA/ARn1-1001020303.615.566.883.475.936.620.945.936.881.083.615.567.384.205.117.382.36×10-64.47×10-61.14×10-54.50×10-42.10×10-32.05×10-60.871.601 05.02×10-62.131.549 61.97×10-58.351.561 24.00×10-60.891.607 36.76×10-61.511.578 17.90×10-61.771.60773.97×10-60.351.597 92.00×10-51.751.607 63.49×10-53.051.558 62.05×10-40.461.604 63.33×10-40.741.629 66.30×10-41.401.561 31.62×10-33.601.587 22.15×10-31.021.512 03.97×10-31.891.571 98.69×10-34.141.600 43-1001020303.115.746.692.735.776.702.755.576.703.405.776.462.825.746.466.93×10-77.34×10-66.93×10-51.96×10-34.73×10-37.15×10-71.031.597 91.01×10-61.461.604 61.01×10-61.461.632 15.23×10-60.711.565 61.47×10-52.001.607 71.13×10-51.541.62146.43×10-50.931.594 69.22×10-51.331.570 28.61×10-51.241.606 11.68×10-30.861.555 16.64×10-40.341.566 25.79×10-40.301.579 45.08×10-31.071.540 43.36×10-30.711.558 34.25×10-30.901.554 1

注：AR为每种沥青混合料在一定温度和空隙率条件下系数A的参考值.空隙率条件：样品1和2的标准空隙率为4.0%，样品3的标准空隙率为3.0%.AR的具体数值都通过回归分析计算得出.

图3显示了在不同温度下，每种沥青混合料的裂纹扩展速度.由图3可知，随着温度的升高，裂纹扩展速率明显加快.换言之，当其他条件不变时，在相对较高的温度下，沥青混合料更容易断裂.同时，由于图3的纵坐标采用的是指数形式，因此，对于每种沥青混合料，在裂纹扩展速度(A值)和温度之间存在近似的指数关系.

同时，由表1可知，随着温度的变化，无论是哪种沥青混合料的n值的变化，几乎可以忽略不计.这表明，n值与温度间的相关性很小.

前述的分析也表明式(3)中J积分可以通过蠕变柔量考虑到沥青混合料的黏弹性，但是它不能完全考虑到温度和裂纹扩展速度的相关性.这是因为蠕变柔量是线性的黏弹性材料的性质.当实验温度变化时，材料的黏弹性和断裂特性都会变化.而蠕变柔量仅能考虑材料黏弹性的变化.

3.2 空隙率的影响

空隙率以直接和间接两种方式影响TD裂纹扩展.直接影响是指空隙率本身就影响材料的断裂特性.空隙导致连续介质产生不连续，它会影响介质的抗裂性.也就是说，较大的空隙率降低了介质的断裂强度.间接影响是指空隙率会影响路面材料的老化程度.因为材料的老化对TD裂纹扩展[14]有较大的影响，所以空隙率会间接影响TD裂纹.沥青混凝土中较大的空隙率不仅会加速材料的老化，也会降低材料的疲劳抵抗能力.因为空隙率对TD裂纹的间接影响涉及现场发生的复杂的老化现象，本研究只考虑空隙率的直接影响.

实验室中可以观察到空隙率对裂纹扩展的直接影响.对于同一沥青混合料来说，如果荷载的振幅和频率一致，在高温条件下，疲劳裂纹扩展更快.相应地，在高温条件下，A值也相对较高.为了清楚地观察空隙率对A值的影响，按照参考A值将表1中的所有A值标准化，得到了A/AR.每种测试温度下不同空隙率的A/AR见图4.

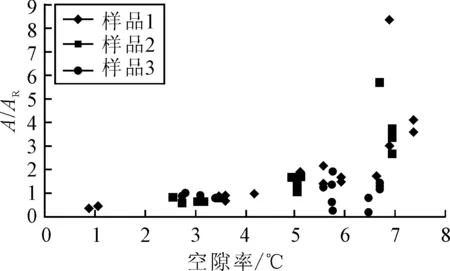
图4 A/AR与空隙率的关系

由图4可知，样品1和样品2的表现较为一致，随着空隙率的增大，A/AR的值也明显变大，表明随着空隙率的增大，这两种材料的裂纹扩展速度明显加快.以样品2在-10℃的表现为例，在该温度下，随着沥青混合料的空隙率增加1.60%，标准化的A值由1.77增加至最大值5.71.这意味着在实验室中，由于空隙率增大了1.60%，裂纹扩展速度可以变快3倍，这是非常显著的变化.此外，对于样品1和样品2，当空隙率接近7%时，A/AR值会陡然增大,因此，在密级配沥青混合料的材料设计中，有必要保证的空隙率低于7%.

与样品1和2不同的是，空隙率对样品3的裂纹扩展没有太大的影响.较大的空隙率并不总是引起裂纹的快速生长.一般来说，在最佳油石比下SMA的空隙率比常规的密级配混合料小,因此，在本研究中，样品3的空隙率均低于7.0%.对于密级配沥青混合料(即样品1和2)，临界空隙率约为7.0%，使得A/AR值突然增加.由于样品1的空隙率均低于7.0%，因此，无法确定，在样品1的空隙率大于7.0%时，是否会发生相同的现象.

通过样品1，2和样品3的不同表现的对比可以看出，由于SMA特殊的集料骨架结构，与密级配混合料相比，其对空隙率相对不敏感，因此，为研究SMA对更高空隙率的敏感度，需要做更进一步的疲劳破坏实验.

由表2可知，与A值不同的是，不管空隙率如何变化，n值的变化几乎可以忽略不计.为了更显著地显示出n值的变化情况，通过回归分析得到每种混合料的平均n值，见表3.

表3 不同类型混合料的平均n值

由表3可知，样品1和3的n值很接近，但样品2的n值有一定差别.样品1和3使用了相同的沥青胶结料PG 64-22，而样品2使用了沥青胶接料PG 76-22.这表明，n值在很大程度上取决于沥青结合料的类型，但与荷载和温度条件无关.

4 结 论

1) 通过使用蠕变柔量，J积分考虑了沥青混合料的黏弹性影响.由于当温度变化时，混合料的黏弹性和断裂特性都会变化，所以J积分不能考虑断裂特性与温度的相关性，如裂纹速度.

2) 一般来说，较高的温度和较大的空隙率会降低沥青混合料的抗疲劳断裂性能.与密级配沥青混合料相比，SMA的抗疲劳断裂性能与空隙率相关性较小.

3) 损伤演化定律的系数n与空隙率和温度的相关性较小；与沥青胶结料的类型相关性更大.

4) 本文成功分析了温度和空隙率对沥青混合料疲劳特性的影响，后续研究可在此基础上修正裂纹扩展模型，并通过进一步的研究来验证提出的模型.