磁梯度张量系统结构的比较分析*

迟 铖,吕俊伟

(1.海军潜艇学院,山东 青岛 266199; 2.海军航空大学,山东 烟台 264001)

现代舰船大多由钢铁材料制成,放置于地磁场中,不可避免地会产生感应磁性,因此可以通过对目标磁场的测量来对舰船目标进行探测、识别和定位。磁探测[1]作为一种被动的目标探测方法,具有隐蔽性好、定位精度高等特点,是探测舰船目标的重要手段,已经成为各国海军研究发展的重点。目前常用的磁场探测方法主要有:磁场总场以及分量场探测、磁场总场梯度探测、磁梯度张量探测等。

磁梯度张量探测[2]最大的优点是能克服地磁场的干扰,提高目标的定位精度。目前常用的磁梯度张量系统主要由超导磁力仪[3]、磁通门磁力仪组成。磁通门磁力仪具有价格低、实用性强等优点而受到广泛关注,目前较为常见的基于磁通门磁力仪的磁梯度张量系统的结构形式主要有十字形[4-5]、三角形[6]、正方形、正六面体[7-8]等,文献[9]采用磁偶极子模型对不同结构形式的磁梯度张量系统进行仿真分析,但是磁偶极子模型是简化模型,文献[10]指出近距离时,磁偶极子模型不能成立,本文采用更接近舰船目标磁场的椭球体与磁偶极子阵列混合模型[11-12]对几种典型结构形式的磁梯度张量系统进行仿真分析,并对影响测量精度的因素进行分析。

1 磁梯度张量

磁梯度张量的定义为磁场三分量沿着空间三个方向的变化率,即

G=B=

(1)

在没有空间电流的区域,磁场的散度和旋度都为零,因此可得如下关系:

(2)

由上式可得磁梯度张量九个分量中只有五个分量是独立的。

2 椭球体与磁偶极子阵列混合模型

首先利用椭球体模型对舰船目标中均匀磁化铁磁物质产生磁场进行模拟,利用磁偶极子阵列对舰船目标的局部磁场进行模拟。椭球体与磁偶极子阵列混合模型如图1所示,设一个长半轴为a,短半轴为b的绕长半轴旋转而成的椭球体,磁化强度为M,坐标系的原点设置于椭球体的中心点位置处,设有N个磁偶极子位于椭球体长轴的轴线上,间隔距离为d。

图1 椭球体与磁偶极子阵列混合模型

椭球体模型产生磁场如式(3)所示:

(3)

式中，

位于(xi,0,0)的第i个磁偶极子在(x,y,z)坐标处产生的磁场为

(4)

式中,ri=(x-xi,y,z)为第i个磁偶极子指向测量点的距离矢量,mi为第i个磁偶极子的磁矩。

椭球体与磁偶极子阵列混合模型的磁场为椭球体磁场与N个磁偶极子产生磁场的矢量合成,由上述磁场的三个分量分别对x、y、z三分量求偏导即可得到磁梯度张量的理论值。

3 磁梯度张量系统

磁梯度张量系统的工作原理为利用相邻两个三轴矢量磁力仪的差值与矢量磁力仪之间距离的比值来近似求取磁梯度张量。差分计算公式如下:

(5)

式中,ΔBi为两个矢量磁力仪i分量之间的差值,Δrj为两个矢量磁力仪在j方向之间的距离差值,该距离定义为系统的基线距离。

不同的磁梯度张量系统的示意图及磁梯度张量的计算公式如下所示。

3.1 十字形磁梯度张量系统

十字形磁梯度张量系统由四个磁通门磁力仪组成,系统的结构如图2所示,1号与3号磁力仪位于x轴上,2号与4号磁力仪位于y轴上。

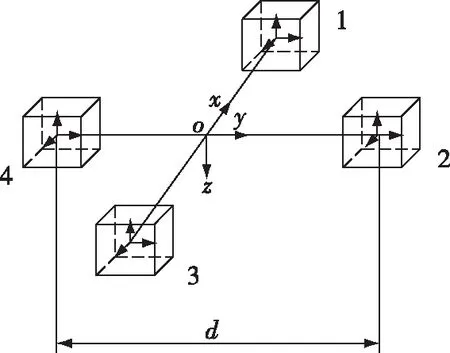
图2 十字形磁梯度张量系统

根据差分方程(5),可得十字形磁梯度张量系统的计算公式如下:

(6)

式中,Bx1代表标号为1的磁力仪所测量的x分量,d为系统基线长度,即同一坐标轴方向上的两个磁力仪之间的距离,十字形磁梯度张量系统不能测量磁梯度张量的全部九个分量,⊗所表示的分量可由式(2)求解得到。

3.2 三角形磁梯度张量系统

三角形结构所需要的磁通门磁力仪的数量最少,系统误差也相对较少,因此成为研究的热点。三角形测量系统由三个磁通门磁力仪组成,分别位于等边三角形的三个顶点。其磁梯度张量系统的结构如图3所示。

图3 三角形磁梯度张量系统

根据差分方程(5),三角形磁梯度张量系统的计算公式如式(7)所示：

(7)

式中,Bx1代表标号为1的磁力仪所测量的x分量,d为系统基线长度,即等边三角形的边长,⊗所表示的分量可由式(2)求解得到。

3.3 正方形磁梯度张量系统

正方形磁梯度张量系统由四个磁力仪组成,分别位于正方形的四个顶点处,而正六面体磁梯度张量系统的每个平面可以看作一个正方形磁梯度张量系统,因此本文以正方形结构为例进行分析,正方形结构示意图如图4所示。

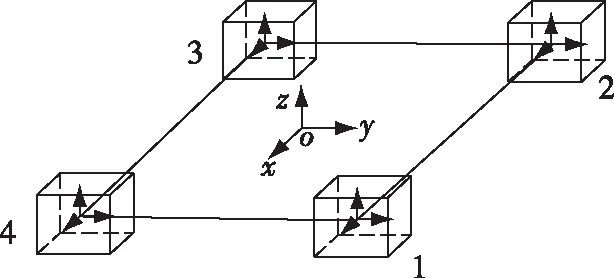
图4 正方形磁梯度张量系统

原点o处的磁梯度张量值为

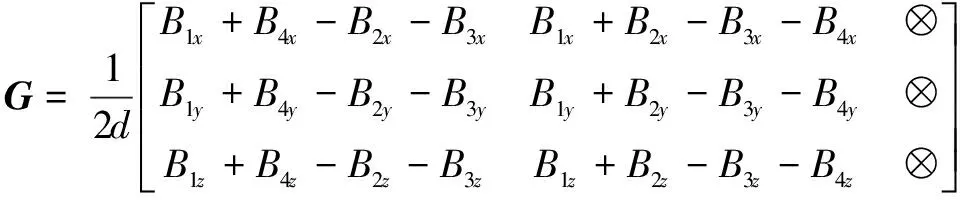
(8)

式中，Bx1代表标号为1的磁力仪所测量的x分量,d为系统基线长度,即正方形的边长,⊗所表示的分量可由磁梯度张量的对称性和无迹性求得。

4 仿真实验

仿真条件设定如下,建立如图1所示的坐标系,混合模型中的椭球体长半轴设为10 m,短半轴设为4 m,磁化强度的大小为1 A/m,在椭球体长轴的轴线上布置7个磁偶极子,相邻磁偶极子间的距离为3 m,磁偶极子的磁矩为(50,20,-50) Am2,磁梯度张量系统的基线距离为0.5 m,磁力仪的精度为0.1 nT,仿真实验时,将磁梯度张量系统从点(-15,1,5)出发,沿着x轴正方向,每隔1 m取一个点,测量得到的磁梯度张量Frobenius范数的测量误差如图5所示。

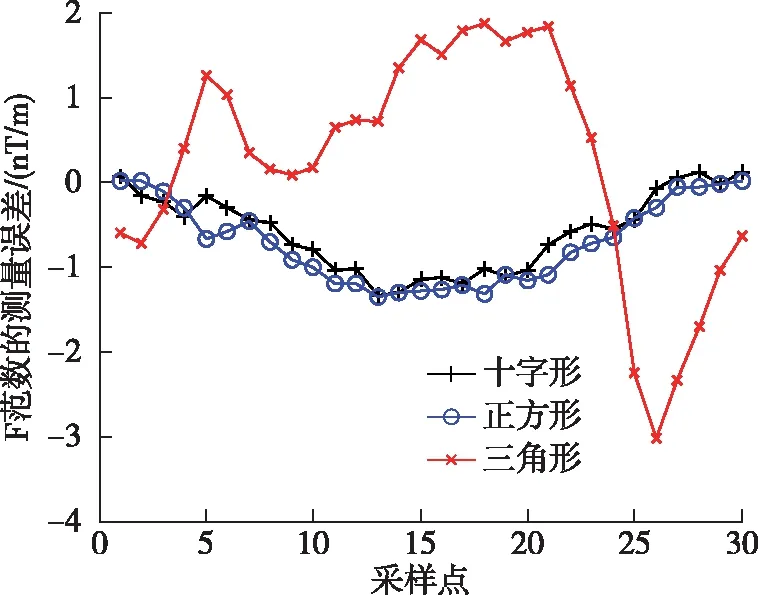
图5 磁力仪精度为0.1 nT、基线距离为0.5 m时的仿真结果

由图5可得,十字形磁梯度张量系统与正方形磁梯度张量系统的误差相对较小,最大的测量误差不超过1.5 nT/m,三角形磁梯度张量系统的误差最大,最大的测量误差超过3 nT/m。

仿真分析当磁力仪精度变为0.01 nT时,基线距离为0.5 m时,不同磁梯度张量系统的Frobenius范数测量误差如图6所示。

由仿真结果可得,随着磁力仪精度的提高,测量误差的波动变小,十字形磁梯度张量系统的测量结果最优,测量误差的最大值为1.2 nT/m,正方形磁梯度张量系统的测量误差最大值为1.4 nT/m,三角形磁梯度张量系统的测量精度最低,测量误差最大值为2.8 nT/m。

仿真分析当系统基线距离变为1 m时,磁力仪的测量精度为0.1 nT,不同磁梯度张量系统的Frobenius范数测量误差如图7所示。

图6 磁力仪精度为0.01 nT、基线距离为0.5 m时的仿真结果

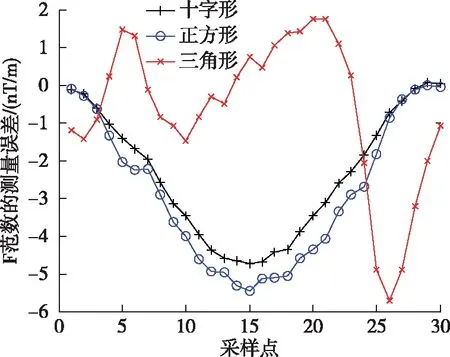
图7 磁力仪精度为0.1 nT、基线距离为1 m时的仿真结果

由仿真结果可得,基线距离增加到1 m之后,不同结构形式的磁梯度张量系统都出现了较大的测量误差,十字形磁梯度张量系统测量误差的最大值为4.7 nT/m,正方形磁梯度张量系统的测量误差最大值为5.4 nT/m,三角形磁梯度张量系统的测量误差最大值为5.7 nT/m。

为了更直观地看出不同系统的测量误差的大小,根据相对误差计算公式：

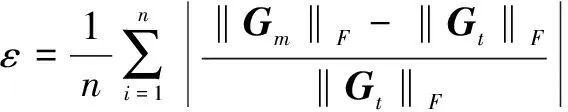
(9)

式中,‖Gm‖F为实测值的Frobenius范数,‖Gt‖F为理论值的Frobenius范数,n为采样点数,利用式(9)得到不同磁梯度张量系统的相对测量误差对比表如表1所示。

由表1可得,十字形磁梯度张量系统的相对测量误差最小,正方形磁梯度张量系统的相对测量误差略大于十字形磁梯度系统的相对测量误差,三角形磁梯度张量系统的测量相对误差最高,随着磁力仪精度的提高,不同结构形式的磁梯度张量系统的测量误差都减小,随着基线距离的增大,测量误差都增大。

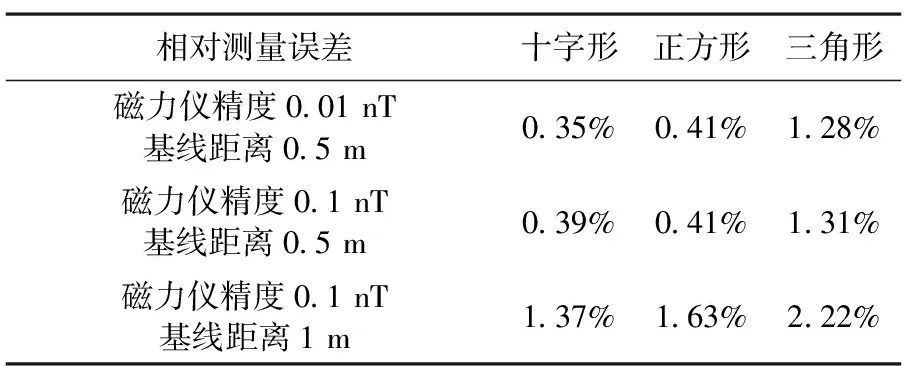
表1 不同磁梯度张量系统相对测量误差对比表

5 结束语

本文首先介绍了常见的几种磁梯度张量系统,接着利用更符合实际舰船磁场的椭球体与磁偶极子阵列混合模型对不同结构形式的磁梯度张量系统的结构误差进行仿真分析。通过分析可得,十字形磁梯度张量系统结构最优,正方形结构次之,三角形磁梯度张量系统的测量误差最大,但是三角形结构具有所需磁力仪最少,且需要校正的系统误差最少等优点,因此需要结合实际情况来对磁梯度张量系统的搭建进行选择。仿真分析得到磁梯度张量系统的测量误差随着磁力仪精度的提高、基线距离的减小而减小,本文的研究结果可为后续的磁梯度张量系统的搭建提供理论参考。