一种基于LMS滤波的单通道窄带干扰抑制平滑算法∗
2019-03-01
(武汉船舶通信研究所 武汉 430079)
1 引言
鉴于现今无线通信的需求,通常利用信道复用的方法来提升有限频谱利用率,其中信道复用具体包括时分复用、频分复用、码分复用等方法。信道复用提升有限频带内的用户容量的同时,由于信道中用户量的增多和信道传输的非理想性,使得通信过程中不可避免地受到干扰(人为干扰及自然环境干扰等)。干扰按照频谱宽度与信号带宽的关系可分为宽带干扰(Wideband Interference,WBI)和窄带干扰(Narrowband Interference,NBI),其中窄带干扰是指干扰所占带宽远小于扩频信号带宽的干扰,包括单音干扰、多音干扰、窄带高斯噪声及同信道的数字窄带信号[1~3]。由于窄带干扰容易产生且频谱峰值极大,通信过程中受到窄带干扰将使得通信系统接收端的信干比下降,会导致通信系统误码率急剧增大,影响通信效能。
为了提升系统的通信效能,需要针对抑制强窄带干扰的方法开展研究。现有的窄带干扰抑制方法大致可分为时域处理方法和变换域处理方法两大类。时域处理方法主要利用了相对宽带信号和窄带干扰不同的可预测性,利用最小均方(Least Mean Square,LMS)算法及递归最小二乘方(Recursive Least Squares,RLS)算法等对干扰信号进行估计。其中,基于 LMS 准则的线性预测算法[4~5,8~11]由于其计算过程简单、收敛稳定,在窄带干扰抑制中有较多的应用。WeePeng算法[6]引入平滑思想,通过对梯度向量的平滑减少噪声对接收机的影响;针对单通道输入的情况,Meyer等在GSM通信中基于单通道输入和BPSK调制讨论了可应用于LMS的干扰抑制方案[7],具有较低的计算复杂度但有一定的局限性。而变换域处理方法根据窄带干扰的能量谱较为集中的频域特性进行针对性的陷波处理,从而剔除干扰所在频带的信号。基于快速傅立叶变换(Fast Fourier Transform,FFT)的变换域干扰抑制技术具有较高的灵活性和便捷性,能够得到较高的线性动态范围,但窗函数的运用会导致频谱泄漏和信号损失[12]。基于小波变换的变换域干扰消除技术[13]由于小波变换优良的时域局域性和多分辨率,对干扰具有较好的抑制效果,同时存在分解层数和计算速度之间的取舍。变换域的盲源信号分离技术能够在缺乏信号与传输参数的情况下依据其统计特性对信号进行恢复,因此学者在单通道盲信号分离技术方面也进行了许多研究,如J.Lee等通过将单通道接收到的数据通过延时方法得到多通道的数据实现多信号分量分离[14];S.Hendari对码速率不同的数字信号在小波域构造与特定码速率信号正交的滤波器来实现单通道MPSK信号的分离[15]等。但由于单通道盲分离是一个极端的欠定盲源分离问题,存在严重的信息不对称,因此现有算法都要求有足够的先验信息或原信号在变换域满足稀疏的假设,同时由于盲信号分离运算量大,并不适合工程实现。
为了解决单天线接收时窄带干扰抑制的问题,在现有单输入LMS干扰抑制算法的基础上,本文提出了一种基于LMS滤波的单通道窄带干扰抑制平滑的方法,首先,将受到干扰污染的信号复制为两路输入;其次以一路信号作为参考信号,另一路信号进行延迟处理后作为主信号利用LMS滤波器进行窄带干扰抑制并获取滤波器响应与参考信号间的差值;最后针对低频单音干扰对输出的差值序列进行平滑处理,旨在解决在无其他参考信号的条件下进行干扰抑制的问题,提升接收机信干比,提高通信质量。
2 系统模型
2.1 窄带干扰抑制系统模型
天线在通信环境中接收信号的过程中同时会受到各种干扰的影响,包括自然环境干扰、周围其他设备产生的工频干扰,及其经过各种反射与散射路径被天线接收到的干扰量。其中,大部分设备的工频干扰及其反射、散射后产生的干扰为窄带干扰。
本文主要研究在信道中窄带干扰能量远大于通信信号的场景中进行窄带干扰抑制的问题。发信端发射的信号进入信道后受到窄带干扰和环境噪声的污染,在接收端使用单天线接收被污染的信号,则接收信号可表示为

其中,s(t)表示通信信号,w(t)表示服从高斯分布的白噪声,i(t)为窄带干扰信号。
窄带干扰信号建模大致分为单音干扰模型和窄带高斯干扰模型。此处选用单音干扰模型,为一列频率固定的正弦波信号,可表示为
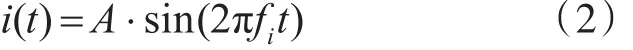
其中,A表示干扰信号的幅度,fi表示单音干扰的频率。
在窄带干扰抑制过程中,首先对接收信号进行预处理,而后送入LMS滤波器进行处理。系统模型框图如图1所示。图中M为自适应滤波器阶数,序列hM(n)为M 维向量,表示n时刻LMS滤波器的系数,即权矢量。 yM(n)为M 维向量,表示n时刻存储在滤波器延时部件中的M个输入信号矢量元素。ˆ(n)表示经过滤波器得到的n时刻预测样值,即自适应滤波器输出响应;e(n)为n时刻自适应滤波器输出误差,作为输出信号r(n)送入后续模块进行处理。
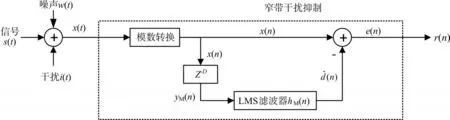
图1 窄带干扰抑制系统
2.2 单天线输入LMS窄带干扰抑制算法
下面对单天线输入的LMS窄带干扰抑制算法具体流程进行描述。
1)初始化
对自适应滤波器系数hM、输入滤波器的信号序列yM做初始化:
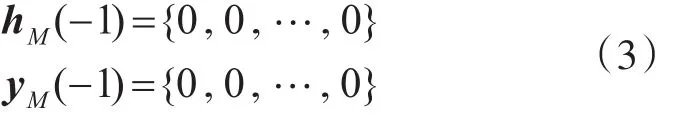
2)样值更新
在n时刻,需要对 yM(n)值进行样值更新,可表示为
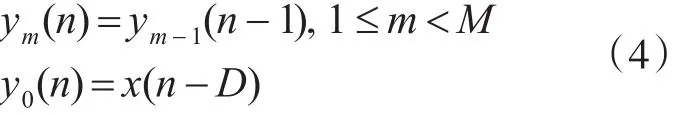
式中 ym(n)表示 yM(n)的第m个分量,0≤m<M ;D为延时参量,表示对信号引入D个采样周期的延时。
在n时刻对LMS滤波器的期望响应进行更新,期望响应d(n)=x(n)。本算法中n时刻的期望响应d(n)的时间坐标应注意与滤波器输出值的时间坐标匹配。
3)求输出响应
n时刻自适应滤
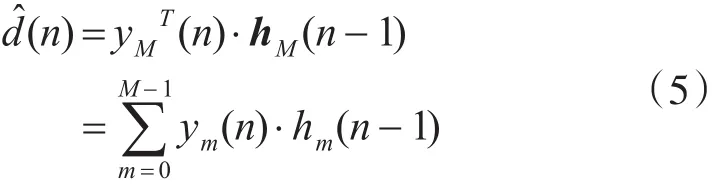
式中,yMT为 yM的转置矩阵,hm(n-1)为(n-1)时刻权矢量的第m个分量。
4)误差比较
根据d(n)求取n时刻自适应滤波器输出误差e(n):

所得e(n)即为所求信号序列。
5)权值更新
更新n时刻的权矢量hM(n):
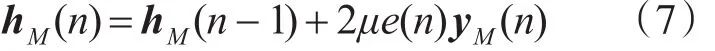
式中μ为迭代过程中的步长:

其中Pin为输入信号的平均功率。
3 基于LMS滤波的单通道窄带干扰抑制平滑算法
本文提出的基于LMS算法的单天线输入窄带干扰抑制算法,在原有算法的基础上引入平滑窗长度L和平滑补偿----em两个参数,针对残存的低频单音干扰进行处理,保证频域平滑,达到优化窄带干扰抑制效果的目的。
3.1 平滑算法推导
由于窄带干扰样值间的强相关性,使得当前值可以用过去的样值进行估计。而携带信息的信号样值之间相干时间较长,相较而言相关性更弱。当接收到的信号同时包含有信号及干扰,在对接收信号进行预测时,由于信号和干扰体现出不同的相关性,在对信号当前值的预测中对窄带干扰的预测值占主要因素。此时只要从接收信号之中减去当前预测值,即相当于减去窄带干扰的预测值。之后对信号进行相应的处理,能够减小窄带干扰对接收机性能的影响,达到抑制窄带干扰的目的,从而提高接收机的性能。
对于LMS算法,若希求最好的信号分离效果,需要求取最小均方误差对应的权矢量,即维纳解w*=R-1P,其中R为输入信号的自相关矩阵,即主信号的自相关矩阵;P为主信号和参考信号的互相关矩阵:
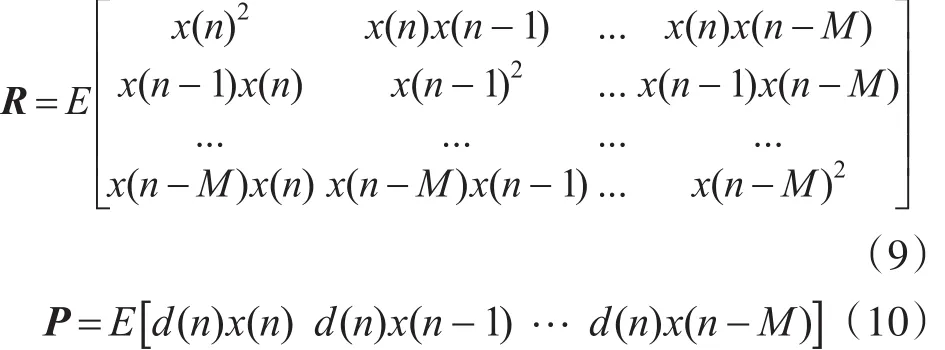
其中主信号为经过延迟的信号,即滤波器的延时参量:
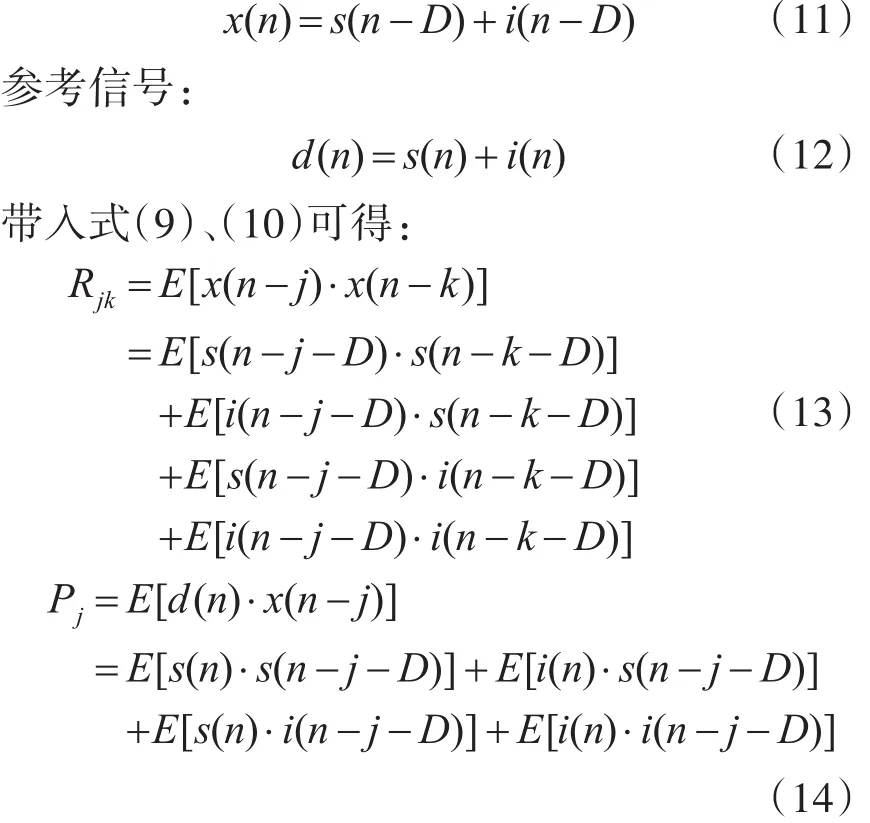
对于式(13),因 i(n)≫s(n),因此认为有E[i(n)⋅i(n-j-D)]是式中的最大项,因此是主信号自相关矩阵的主要参量。对于式(14),当所设置的延迟参量D大于需求信号s(n)的相干时间时,易得 E[s(n)⋅s(n-j-D)]=0 ;又 因 i(n)≫s(n),有E[i(n)⋅i(n-j-D)]≫ E[i(n)⋅s(n-j-D)] 和E[i(n)⋅i(n-j-D)]≫E[s(n)⋅i(n-j-D)],可 知 带 内干扰i(n)是影响维纳解w*的主要参量。在特殊情况下,会出现i(n)与in-j-D正交即E[in⋅in-j-D]=0的 情 况 ;此 时 式 中 仅 E[i(n)⋅s(n-j-D)]和E[s(n)⋅i(n-j-D)]两项非零,由于 i(n)≫s(n),从而仍可认为带内干扰i(n)是影响w*的主要参量。
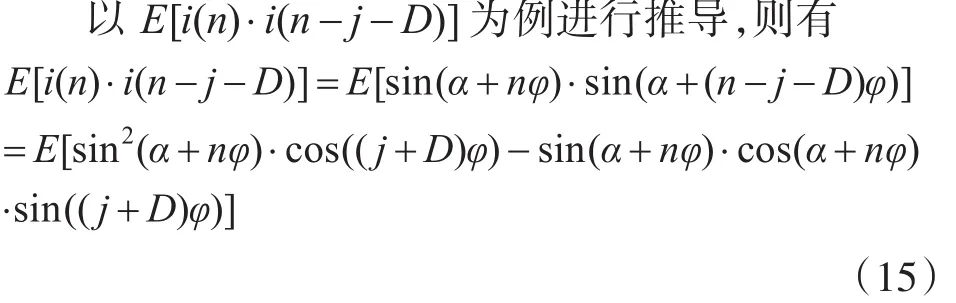
其中,α为i(n)序列的初始相位,即起始时刻信号i(0)的相位,通常视为常数。处理过程中D大于需求信号 s(n)的相干时间,0≤j<M 。 φ=2πfi/fs表示每个单音干扰采样点的相位增量。则对于每个n和 j的取值而言,期望的计算结果仅与φ值相关,由于系统中的接收端采样频率 fs已知,因此φ只与单音干扰频率 fi有关。由于相同的迭代过程中,n和 j的取值情况总是一致的,则可认为w*由fi决定。
此时LMS滤波器的频率响应函数为
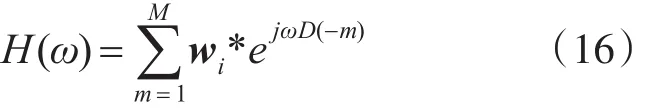
其中wi*是维纳解w*的第i个分量。可见,此时LMS滤波器在带内干扰i(n)频率 fi附近体现为通带,在其余频点体现为阻带。
因计算开销所限,在信号处理过程中通常不会长时间持续进行自适应过程的迭代计算,在认为信道慢变的一段时间内可能只在初始时间段内进行滤波器权值的更新。因此,在某些情况下训练阶段无法对单音干扰的特征做到完全掌握。虽然这一问题可以通过增加迭代次数得到部分改善,但迭代次数过多会有损系统处理过程的实时性,且由于迭代过程的固有硬件开销,在工程中较难实现。
在实际应用中可以发现,当 fi较高时,通过LMS自适应滤波已经能较好地滤除单音频率 fi的干扰。当 fi较低时,在同样的迭代次数结束后,窄带干扰抑制性能与 fi较高的情况相比较差。此处fi的相对高低与输入自适应窄带干扰抑制模块信号的采样频率 fs与设定的模块迭代次数Li相关,这两个参数在系统设计时已经确定,因此视为已知信息。
对于 fi≫fs/Li的情况而言,由于单音信号采样点幅度值的变化较快、单个波形周期持续时间短,因此在较少的迭代次数中获得的滤波器权值hM已经能较好地体现出单音干扰周围的通带效果。而对 fi较低的情况而言,此时带内单音干扰是一低频正弦波信号,由于单音干扰波长较长,在一段较短时间内可认为是缓变的信号,在较短时间内难以完全体现其频域特性,因此在滤波器的迭代阶段结束后滤波器权值序列hM在单音干扰频率 fi附近通带体现不明显,针对干扰的处理性能较差。但同时由于干扰采样点的幅度是缓变的,一段时间内可以看作直流信号,因此在一段信号s(n)均匀分布的时间T内求e(n)的均值所得的平均值eˉ可以看作是时间T内的持续直流偏置信号:
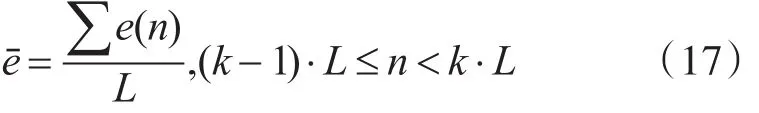
其中L表示时间T内的信号采样点数即平滑窗长度:

针对该段时间T,去除直流偏置补偿量即为信号e(n)进一步对低频单音干扰进行抑制后的估计值:
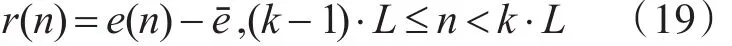
3.2 基于LMS滤波的单通道窄带干扰抑制平滑算法
文中基于LMS滤波的单通道窄带干扰抑制平滑算法系统模型框图如图2所示。
在接收到信号并做相应采样处理后,因为信号中含有需求信号与带内单音干扰,因此可表示为
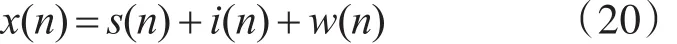
对各参数进行初始化。根据发端信号已知特性,确定延迟时间长度D,D取值需大于信号s(n)的相干时间,从而保证 E[s(n)⋅s(n-j-D)]=0对所有能取到的 j均成立;同时根据已知的发端信号参数及调制方式确定后续平滑窗长度L。
对信号 x(n)进行LMS滤波,权矢量长度为M ,迭代次数Li,步长按

确定,使用小步长可以增加收敛过程的稳定性。将输入信号x(n)复制为两路,一路成为主信号,另一路经D延迟处理后成为期望响应。
对于n时刻,更新当前抽头输入向量 yM和期望响应d(n),计算LMS滤波器输出对输入信号的响应:
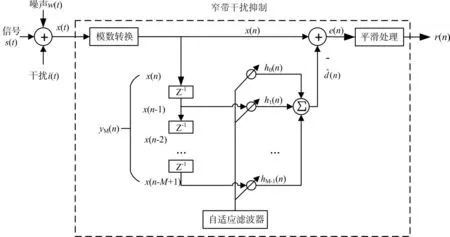
图2 窄带干扰抑制系统
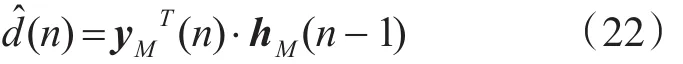
将输出响应与期望响应进行比较获得估计误差:

并根据估计误差调整滤波器抽头权值
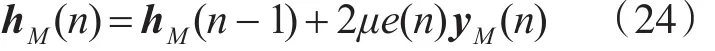
在迭代次数Li范围内对抽头权值进行循环更新,训练结束后停止对hM的更新,固定hM为常数值继续进行滤波过程。
由前述可知,此时权矢量主要由带内干扰分量i(n)影响,从而LMS滤波器的输出信号与i(n)接近,下一步两信号相减之后结果与s(n)趋近,从而滤除带内干扰i(n)的大部分能量。
对e(n)进行平滑处理,对每L个值求取其平均值:

针对这一段信号进行补偿:
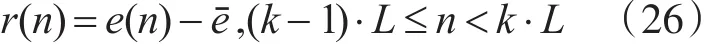
最终获得信号r(n)。
4 仿真与性能分析
为了验证算法的有效性,本文对窄带干扰抑制算法进行蒙特卡罗实验仿真分析,仿真中通信信号s(t)采用扩频信号,信源编码采用速率为1/2的卷积码,信道编码采用Walsh正交调制;干扰信号i(t)干扰为带内单音干扰,即频率范围处在携带信息的信号带宽范围之内的单音信号;白噪声信号w(t)服从均值为0、方差为1的高斯分布。接收端对所获信号进行采样后获得数字信号,并送入干扰抑制模块。仿真中以自适应干扰抑制方法的处理增益作为评价标准。处理增益即为自适应干扰抑制模块前端输入信号的输入信干比与经处理后信号的输出信干比的差值。
仿真1对本方法在一定信噪比、不同信干比情况下的性能进行仿真分析。仿真中信噪比为-5dB,计算精度为32位定点计算,由于实际工程中干扰严重时,信干比通常在-20dB~-30dB左右,本仿真将输入信干比取为[-40,30]dB。仿真结果如图3所示,对于不同的输入信干比,在本算法有效范围内,输入信干比越低则处理信干比增益越高。总体而言,经该方法处理过后,系统的输出信干比能够被提升至-3dB左右或更高。对于适用的经Walsh调制信号,鉴于其存在较高的扩频增益,因此在输出信干比为-3dB时已经能够获得较好的译码效果。
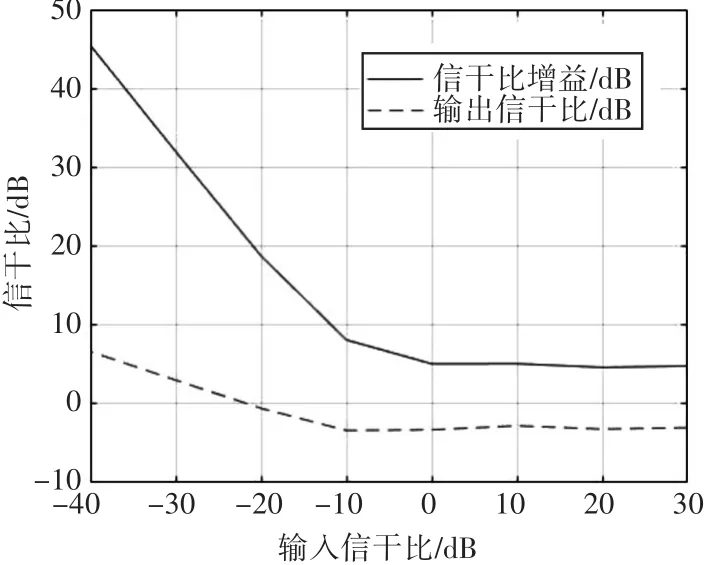
图3 处理增益分析
仿真2对本算法在不同量化位数的情况下的性能进行了仿真分析。仿真过程中设定计算字长分别为16位、20位、24位、28位、32位,单音干扰频率 fi分别为50Hz和1500Hz,信干比分别为-10dB和-20dB,对信干比增益进行仿真。仿真结果如图4所示,在自适应干扰抑制过程中计算字长将对抑制方法的处理增益产生影响,字长越长,计算的精度越高、量化误差越小,本方法的处理增益越高。16位字长计算得到的处理增益明显低于较长字长计算得到的结果。同时,对于不同的信干比,由于信号的归一化导致了携带信息信号绝对值下降,有可能出现信息被淹没在量化误差中的情况;因此在较低输入信干比的环境中,短字长计算的性能下降尤为明显。而在实际工程应用可能出现的输入信干比范围之内,以20位、24位、28位、32位字长进行计算的处理信干比增益差距不大。
仿真3对平滑处理步骤为本方法带来的处理增益进行探讨。以32位字长进行计算,设置输入信干比为-20dB,对本步骤在不同频率单音干扰下提升的信干比处理增益进行仿真,迭代次数分别为2000和4000次。仿真结果如图5所示。
可见,平滑处理能够在信道受到较低频率单音干扰污染的情况下有效提升干扰抑制算法的处理增益。在所受到单音干扰的频率较低时,平滑处理能够有效提高本方法的处理增益。同时对后续较高频率单音干扰的处理情况进行了仿真,确定平滑处理对此情况下的算法性能不造成损害。
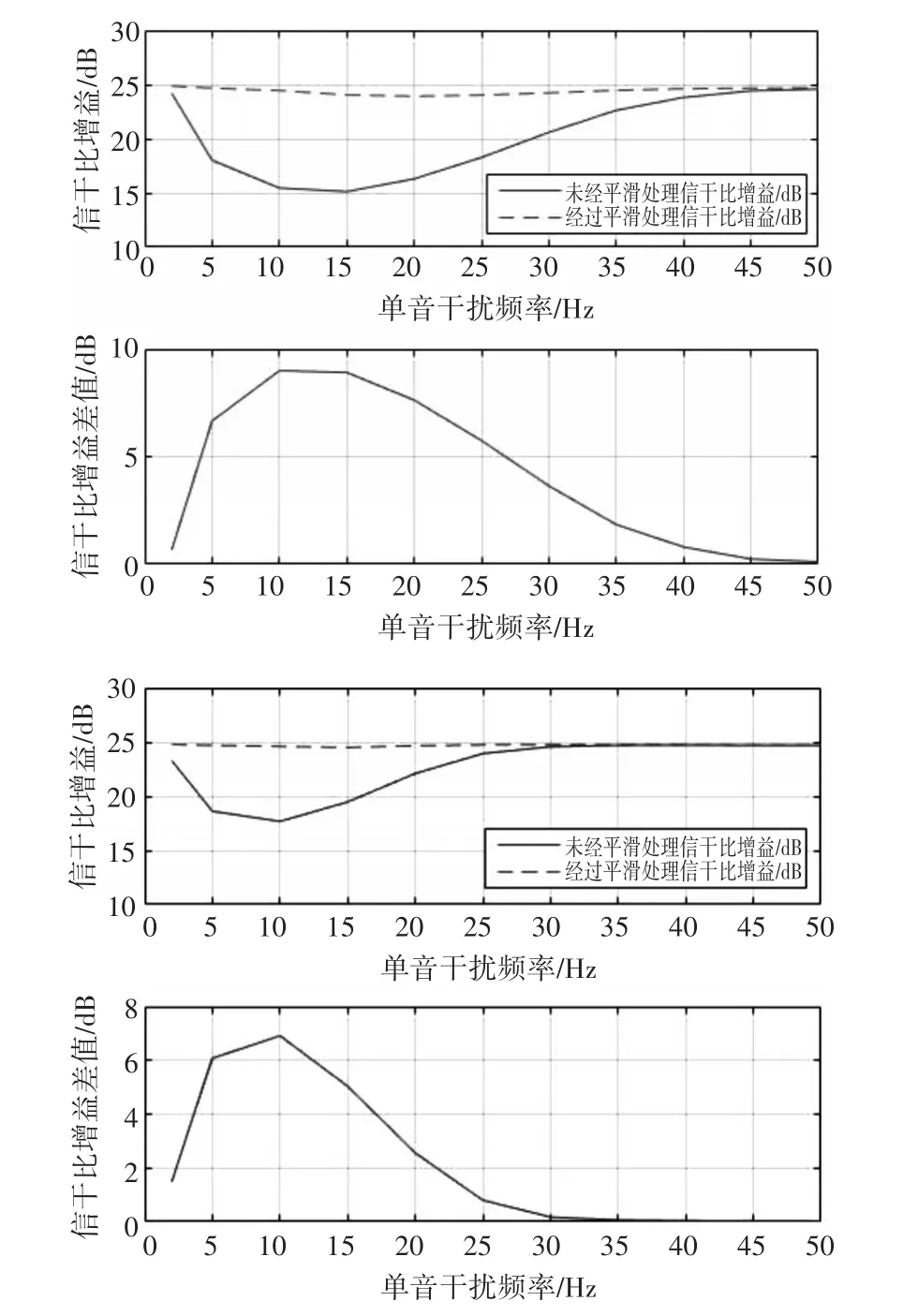
图5 平滑处理增益
5 结语
本文针对现有单输入LMS干扰抑制方法在低频干扰下性能较差的缺点,提出了一种基于LMS滤波的单通道窄带干扰抑制平滑算法,将单输入LMS干扰抑制和平滑处理方法有机地结合在一起,通过LMS滤波抑制高频单音干扰,通过平滑处理抑制低频单音干扰,从而提升接收机性能。通过仿真分析可知,本文提出的基于LMS滤波的单通道窄带干扰抑制平滑算法,在低频单音干扰环境下较现有单输入LMS干扰抑制方法性能更好,而在高频单音干扰环境下与现有单输入LMS干扰抑制方法相比无性能损失;并对有限字长效应对本文方法的影响进行了仿真,为其工程实现提供了理论依据。
