动态网络社区发现算法研究

2019-02-27胡北辰

长春师范大学学报 2019年2期

胡北辰

(安徽电子信息职业技术学院，安徽蚌埠 233000)

移动通信网络、淘宝等电子商务网络、社交网络等都有一个特性，即它们都是动态的。根据eMarketer的最新统计预测，2017年，80%的中国网民经常访问社交网络，大概为6.62亿人，其中4.83亿网民常用手机访问社交媒体。如此庞大的网络结构已经很难凭直观来挖掘有用的信息，社区发现算法能够对社区内某些具有共性的信息特征进行分析，使得人们能够更好地利用社区发现研究结果，例如，在疾病控制中心网中，可以根据社区结构有针对性地加强对疫苗的控制，从而降低成本。

1 经典动态社区发现算法

1.1 GraphScope算法

GraphScope算法[1-3]，是通过合并不同时间片的图结构从而获取到新图，并对生成的新图应用社区发现。算法的具体过程：判断新的时间片是否为改变点，若是则开始新的时间片并单独进行发现社区，且不对网络的变化进行关注；若不是则合并当前时刻和该时间的图结构来获取新的图，并在新图中应用社区发现算法，合并后的新图拥有网络变化的各时刻信息，同时会持续考虑网络的动态变化情况。

1.2 FaceNet算法

FaceNet算法[4-6]，是当前时间片t执行社区发现算法，随之根据t-1时刻来调整时间t的社区结构。该算法分为两个步骤：首先对当前时间片执行社区发现算法；应用极值优化方法调整t时刻社区结构，将社区结构划分成二分图，得到节点相似度矩阵，最终社区发现算法转化为最小化cost目标函数问题。

1.3 QCA算法

QCA算法[7-8]，是经典的自适应增量式处理网络动态变化的方法，其t时刻的社区结构是基于上一时刻t-1和t时刻两者之间的网络变化而演化生成的。

2 QCA算法的优化

GraphScope算法和FaceNet算法在每一个时间片都需更新网络图和重新划分社区，但一般情况下相邻的社区不会发生很大的变化，因此这些算法会造成社区划分计算时间过长。QCA算法应用的是时间片递增变化处理方法，仅对变化的网络部分进行计算，因此可以提高算法的效率，但会降低算法的准确率。因此接下来将对QCA算法进行优化。

2.1 符号定义

定义社会网络是无向图G=〈V,E〉，V={v1,v2,…,vn}是网络节点集，vi表示i节点；E={eij|vi,vj∈V,i≠j}是网络边集。社区结构为C=C1∪C2∪…∪Ci，i=1,2,…,k，Ci表示i社区。由于动态网络任一时刻都在变化，因此定义Gt为t时刻的社会网络，Ct为t时刻的社区结构。

下面首先定义相关的概念：

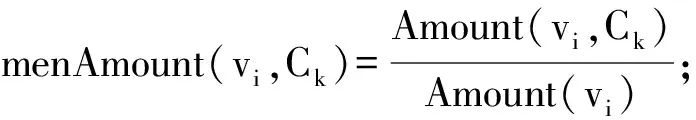
网络节点vi在Ck的t时刻：Not(vi)=Ck；

当网络节点vi所在的社区条件发生了变化时，ε是用户定义的menAmount(vi,Cq)比例值：menAmount(vi,Cq)-menAmount(vi,Cp)≥ε.

2.2 QCA优化

假设在动态网络的变化过程中，若相邻的时间片段变化差异较小则表示仅有少量的网络节点需要重新计算社区划分。本文着重研究相邻社区的节点变化，并根据时间片段的前后变化来计算时刻t的社区结构。

2.2.1 增加边

在t时间段，首先在动态网络节点a、b中间添加一条边，且Not-1(a)=Cq,Not-1(b)=Cq，接下来讨论添加的边对各节点的影响。

(1)p=q表示节点a、b在同一社区，和其它的社区没有连接，且不会对节点所属社区产生影响，但应加强节点间的联系来提高紧密性。

(2)p≠q表示节点a、b属于不同社区。接下来进一步分析节点能否改变社区的划分：

Amount(a)=Amount(a)+1;Amount(b)=Amount(b)+1;Amount(a,Cq)=Amount(a,Cq)+1，通过节点更新比例值来判断节点a从Cp转移到Cq的可能性；

(3)若menAmount(a,Cq)-menAmount(a,Cp)<ε，则节点a不可能转移到Cq，即接下来讨论节点b的可能性：①若Amount(b,Cp)=Amount(b,Cp)+1，则需要看节点b转移到Cp的可能性；②若menAmount(a,Cq)-menAmount(a,Cp)<ε，则结束当前操作，节点b无法进行移动；③若menAmount(a,Cq)-menAmount(a,Cp)≥ε，则将节点b转移到Cp，并更新相邻节点。

2.2.2 删除边

若动态网络中，在t时间段，边eab将被删除，接下来讨论添加的边对各节点的影响。

(1)p≠q表示节点a、b属于不同社区，删除节点a、b之间的边不会改变社区，会降低社区间的耦合度，因此仅需更新参数即可。

(2)p=q表示节点a、b为同一社区。①删除节点a、b之间的边后，节点a、b分别会成为独立的社区，则变化过程为：Amount(a)=Amount(a)-1;Amount(a,Cq)=Amount(a,Cq)-1,Amount(b)=Amount(b)-1;Amount(b,Cq)=Amount(b,Cq)-1.C=C∪Ck,Not(a)=Ck，同时更新节点b的社区值，若有某社区Ci符合menAmount(b,Ci)-menAmount(n,Cp)≥ε，则更新节点b的相邻信息。②删除节点a、b之间的边后，并没有形成社区，因此需重新计算节点a、b的权值来确定它们的归属。判断节点a是否满足移动要求，若menAmount(a,Cq)-menAmount(a,Cp)≥ε，则更新相邻的节点，否则对节点b进行判断，若menAmount(b,Cq)-menAmount(b,Cp)≥ε，则更新相邻的节点。

2.2.3 添加点

若设在t+1时刻时，在动态网络中插入节点v，接下来探讨两种情况：

(1)节点v不与任何社区相连，则将节点v设置为社区Ck，且E不变，需要进行如下计算：V=V∪v;C=C∪Ck。

(2)节点v和某一个或多个社区中的一个或多个节点相连。在添加节点v之前，需要计算节点v原来社区的权重值，若Amount(v,Ck)为最大值，则v∈Ck。若网络中的总社区不变，则设w为v的任一连接节点，需要进行如下计算：V=V∪v;E=E∪evw。

2.2.4 删除点

若设在t+1时刻时，在动态网络中删除节点v，接下来将探讨两种情况：

(1)节点v不与任何社区相连，即∀w∈V,∀evw∉E，则将节点v设置为社区Ck，且E不变，需要进行如下计算：V=V-v;C=C-Ck。

(2)节点v和某一个或多个社区中的一个或多个节点相连，则∀w∈V,∀evw∈E。若网络中的总社区不变，设w为v的任一连接节点，需要进行如下计算：V=V-v;E=E-evw。

3 实验结果分析

将真实的网络结构作为研究对象，收集动态网络中电子邮件的发送情况，时间为不同的10个时间段，相邻的时刻网络变化极少。通过文献[9-10]分析可知，当ε=0.1时，社区结构的稳定性和社区特征能够达到很好的效果。

将动态网络静态化，采用GN算法将社区划分为10个时间的静态网络，划分后的社区结果如表1所示。

表1 GN社区划分表

采用优化后的QCA算法与经典的GraphScope算法和FaceNet算法比较社区划分情况(表2、表3、表4)。

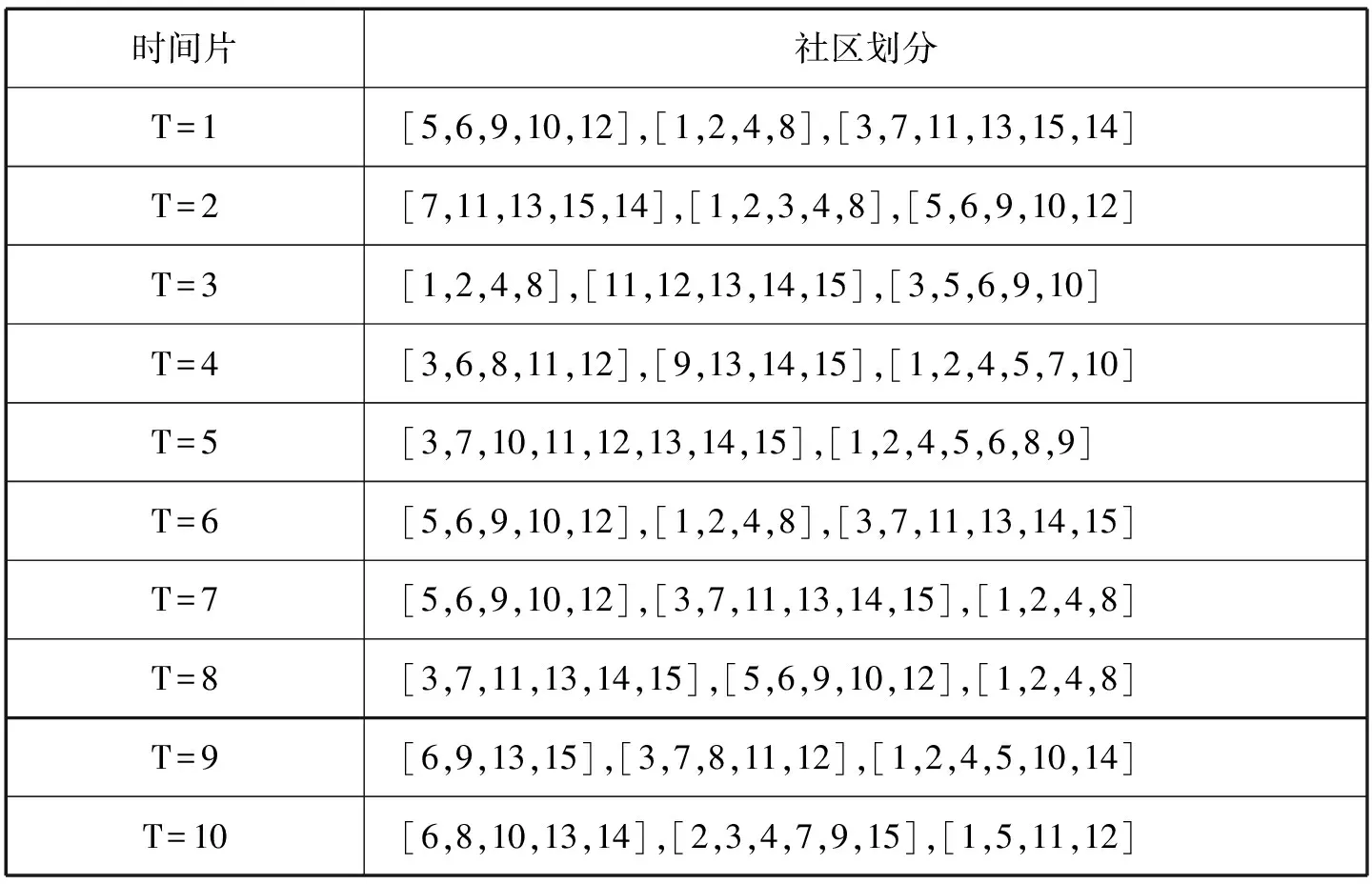
表2 GraphScope算法社区划分表

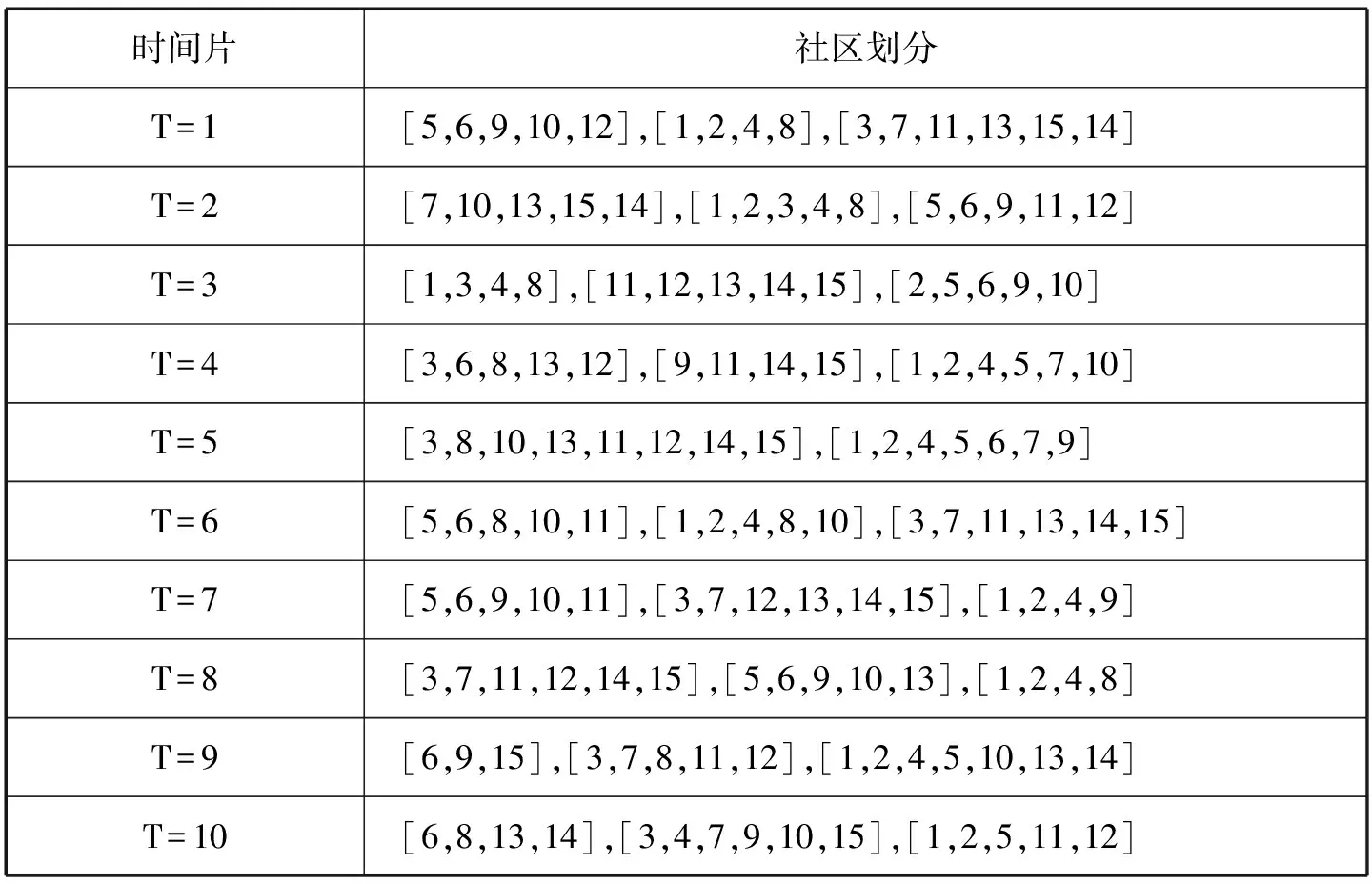
表3 NetFace算法社区划分表

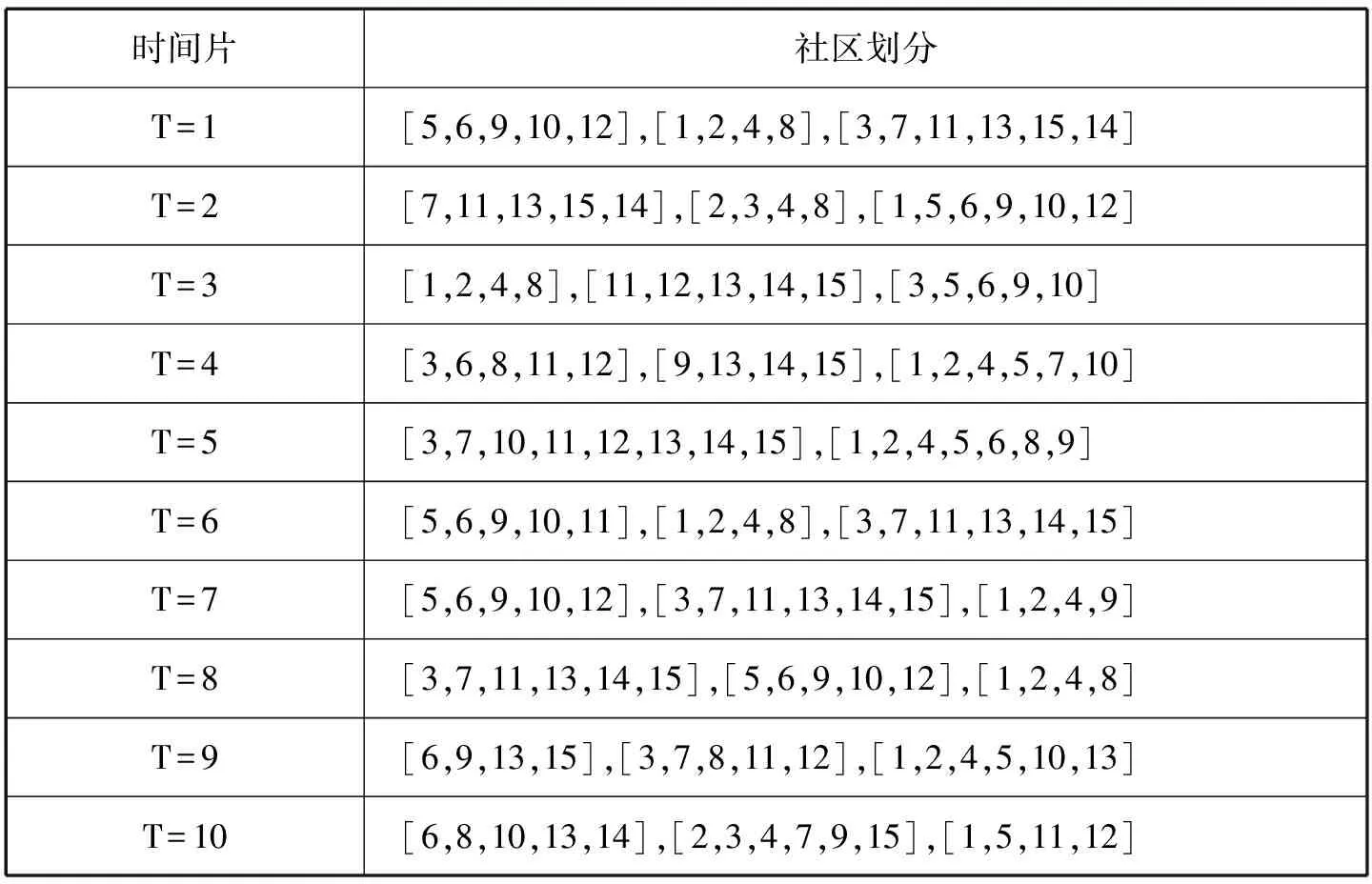
表4 优化后的QCA算法社区划分表

T=9时刻，GraphScope算法的社区划分分别为：[6，9，13，15]，[3，7，8，11，12]，[1，2，4，5，10，14]；NetFace算法的社区划分分别为：[6，9，15]，[3，7，8，11，12]，[1，2，4，5，10，13，14]；优化后的QCA算法的社区划分分别为：[6，9，13，15]，[3，7，8，11，12]，[1，2，4，5，10，13]。这表明不同的算法划分的社区是不同的。

运用社区结构质量、准确率、平均时间来直观地比较各种算法，如表5所示。采用优化后的QCA算法能够得到较好的社区结构质量、较好的准确率和更少的平均时间。