多级优化BP 神经网络的异常流量检测

文/陈胜 朱国胜 祁小云 雷龙飞吴善超 吴梦宇

随着“互联网+”时代的发展，网络的规模越来越大，网络安全问题也变得更加复杂。因此，有效准确地识别异常流量对网络安全起到关键的作用。异常检测的网络流量数据具有数据量大和随机性强的特性，传统基于特征规则、统计和阈值的异常检测系统检测效率低、模型更新代价大、难以检测未知的异常，不易建立检测模型，在复杂多变的网络环境中难以满足安全检测的要求。而神经网络对模拟人类神经系统的模型有很强的认知能力，是进行高效率异常检测分析的较好选择[1]。

BP神经网络算法具有良好的自学习、自演化和非线性映射能力，能够在不熟悉网络环境和异常流量背景信息的情况下对复杂多变的异常流量训练，并能快速地检测未知的异常流量，是一种满足当今网络异常检测的方法[2]。但是纯粹的BP 神经网络模型存在一些不足，比如收敛速度慢和容易陷入局部最优解等问题。如果直接将BP 神经网络算法应用到异常流量检测中会使系统出现较高的误报和漏报情况，从而使检测的效率达不到保障网络安全的要求。针对这些问题，研究人员采用了很多方式去优化BP 神经网络算法，例如：傅德胜[3]采用全局优化算法的粒子群优化算法来优化BP 神经网络检测模型。王龙[4]采用人工蜂群优化算法来提高BP 神经网络对网络异常检测的准确率，减少BP 神经网络算法的迭代次数，加快收敛速度。可是这些使用全局优化算法进行一级优化BP 神经网络的模型会出现早熟收敛、到后期会出现收敛速度变慢、精度误差达到一定时难以继续优化等问题，使异常流量检测的效率、准确性和适应性没有达到高标准的要求。

本文提出一种多级优化BP 神经网络的异常流量检测方法，使用人工蜂群算法对BP 神经网络的权值和阈值进行优化，当雇佣蜂达到人工蜂群迭代次数后，再使用粒子群算法在当前最优值和拓广的全局范围中进行二次搜索优化。该方法能有效解决BP 神经网络收敛速度慢和易陷入局部最优等问题，并能解决人工蜂群算法中没有依据先验知识的角色转换性能不足的问题[5]，从而使异常流量检测的精准度更高、误报和漏报率更低，提高异常检测系统的效率和适应性。

算法模型

BP 神经网络算法

BP 神经网络是神经网络中应用最为广泛的多级网络，是一种按照误差反向传播训练的多层前馈网络。BP 神经网络是由输入层、隐含层和输出层三个部分构成。其中输入层是输入特征向量，输入向量不需要知道事物之间的相关关系，每一个节点代表一个类型，通过BP 神经网络的自学能力来发现它们的映射关系。在隐含层上各个隐含节点之间是没有连接关系的，它只与输入、输出层有连接关系，可以看成是进行向前传播和向后传播的中介层。输出层是看实际输出和期望输出相差是否在误差范围内，如果在误差范围内，则BP 神经网络模型结束迭代将实际输出。如果不在误差范围内，则误差信号沿反向传播到输入层，同时修改映射之间的权值和阈值，然后在重新正向传播[6]。

设输入层的输入向量X=（x1，x2，x3，…xn），wij、θij分别为输入层到隐含层的权值和阈值。因为神经元所使用的激活函数必须处处可导，所以本文选用最常使用的S 型函数，隐含层的输出yj 如下式：

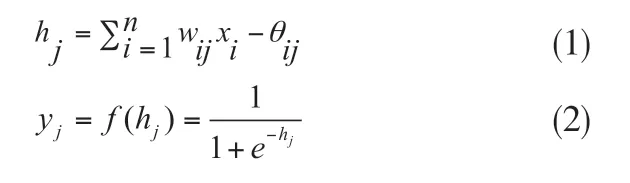
在反向传输的过程中，先计算神经网络的误差：

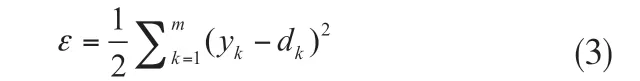
然后根据误差要求来调整隐含层到输出层的权值和阈值：

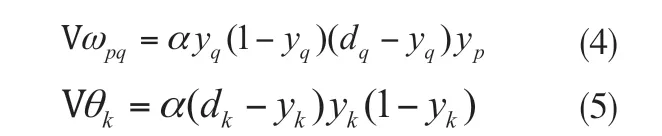
上面（4）和（5）式中的ɑ 是指学习速度。

由以上过程逐渐迭代训练，发现BP神经网络具有很强的自学习、自演化能力。因此，将BP 神经网络应用到异常流量检测中是明智之举。但是，单纯的神经网络算法会出现收敛速度慢、易陷入局部最优解，在异常流量检测中会存在较高的误报和漏报率、精度不足等情况，从而影响异常流量检测的效果。为解决神经网络的不足，本文提出了一种人工蜂群和粒子群多级优化BP 神经网络的方法。

人工蜂群算法

人工蜂群优化算法（ABC）是模拟蜂群中各个蜂种分工合作并将信息进行分享的采蜜过程，从而找出问题的最优解。在ABC 算法中由食物源、雇佣蜂和非雇佣蜂三个部分组成，其中非雇佣蜂又可以分为观察蜂和侦查蜂。整个算法的目的就是寻找花蜜量最大的食物源[7]。

假设在N 维空间中有S 个食物源，第i 个食物源的位子为Xi（xi1，xi2，…，xin）。每个蜜源的位置是一个解，每个蜜源的花蜜量对应该解的适应度。先初始化S 个食物源，雇佣蜂根据食物源信息寻找新的食物源，然后再跟观察蜂分享信息，从而来更新食物源位置。如下式：

其 中i=1，2，…，S，d=1，2，…，N，rand(-1，1)是取[-1，1]的随机数，i ≠k。

观察蜂会估计每个雇佣蜂带来的食物源信息，并根据适应度函数来选择概率高的食物，由下式来计算概率：

其中：fiti是第i 个解的适应度。当某个食物源在规定的侦查次数内没有更新时，为了防止出现局部最优解，侦察蜂会根据下式来更新解

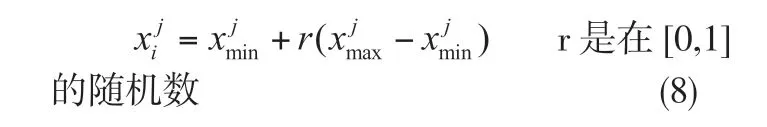
通过以上的过程分析，人工蜂群算法的正反馈机制使算法具有很强的全局搜索能力和较快的收敛速度，但是在角色转变时局部信息考虑不足使算法后期收敛速度变慢，影响算法性能不足的同时使异常流量检测模型的误报和漏报都较高，从而该模型不能满足复杂的网络环境检测。因此，本文结合粒子群算法一边考虑当前最优解，一边结合全局搜索，再一次来优化异常流量检测模型。

粒子群算法

粒子群优化算法（PSO）是源于对鸟群捕食行为中个体协作和信息分享来寻找最优解的过程。其中每个粒子都是PSO 优化问题的一个解，都有被目标函数优化决定的适应值和它们向某个方向飞行的速度和距离，然后粒子根据当前最优信息在拓广的空间范围内搜索全局最优解[8]。

PSO 初始化为一群随机的粒子，假设第i 个粒子在N 维空间的位置向量和速度向量分别为Xi=(xi1，xi2，…，xin)和=(vi1，vi2，…，vin)，该粒子在当前发现自己经历的最好位置为pbest，整个粒子群中经历最好的位置为gbest。粒子在每次迭代过程中会根据pbest和gbest来更新自己。粒子会根据下面的式子来更新其位置与速度：

在（9）和（10）式中：k 代表的迭代的次数；w 是粒子的惯性因子，c1 是局部学习因子，c2 为全局学习因子，r1 和r2 在区间（0，1）范围内的随机参数。为了防止粒子的速度太大，通常设置一个速度范围[-Vmax，Vmax]，当Vi>Vmax 时，Vi=Vmax，反之亦然。PSO 算法没有角色转换，具有信息记忆功能、结构简单和收敛速度快等优点，使用PSO 算法优化人工蜂群转换的角色，让异常检测模型进一步提高检测正确率和检测效率，能实现高要求检测的网络环境。

多级优化算法

ABC 和PSO 算法是群智能的全局优化算法。ABC 算法具有收敛速度快，检测精度高的优点，但是在后期有寻优速度会变慢、对局部信息考虑不全等缺点。PSO有算法结构简单、收敛速度快和先验知识的记忆能力等特性[9-11]。因此，本文结合两种算法的优点采用PSO 算法的全局收敛速度快的特点去优化ABC 算法在后期收敛速度慢和陷入局部极值的缺点，再用得到的优化算法去优化BP 神经网络的权值和阈值，进而解决神经网络模型的精度低和收敛速度慢等问题。

ABC 和PSO 算法多级优化BP 神经网络的过程如图1 所示。

图 1 多级优化BP 神经网络的流程

算法具体过程如下：

1. 流量数据集预处理和特征选择，随机选择训练数据作为训练样本，初始化生成BP 神经网络的输入层、隐含层与输出层之间的权值和阈值，选择特定的流量特征作为神经网络输入特征。通过公式（1）、公式（2）计算输出的实际值。

2.由公式（3）计算出BP 神经网络的误差。当误差满足设定的值时结束训练输出权值和阈值，反之继续下一步。

3. 根据计算的误差通过公式（4）和（5）调整输入层、隐含层与输出层之间的权值和阈值。然后再执行步聚1、2，如果误差满足要求结束训练，否则继续。

4.将流量特征经过BP 神经网络计算得到的特征权值和阈值作为ABC 算法的输入，设定神经网络的误差作为ABC 算法的适应度函数，初始化ABC 算法。

5.根据公式（6）、（7）对食物源的信息进行更新。若满足设定的迭代次数，输出最优的食物源信息执行步聚7，否则继续搜索。当某个解达到搜索的上限后，雇佣蜂会转换成侦查蜂进行PSO 优化，执行步聚6 得到最好的食物源解。

6.根据当前解信息拓广粒子群的搜素范围，设定迭代次数，初始化每个粒子的速度和位置。按照粒子群搜索的方式更新粒子的最优值，当满足最大迭代次数时，用新食物源的位置更新原食物源的位置同时进入下一步，反之继续迭代搜索。

7.将得到的食物源信息作为BP 神经网络的权值和阈值去重新训练，转到步聚3。结束训练后，将得到的训练模型进行测试。

实验部分

数据预处理

实验数据采用麻省理工学院林肯实验室入侵检测评估项目的数据集，此数据集现今依然被广泛使用异常检测比赛和异常检测系统评估。“KDD CUP 1999 Data”数据集[12]中每个连接都有42 项字段，其中前41 项是特征属性，最后一项是类型的标记属性，标记的是一个正常流量类型和22 种具体攻击类型。异常类别是与用户行为存在密切关系，数据集的41 特征属性中有许多特征是冗余特征，这样会影响异常检测模型的准确率[13]。因此，为了提高检测的效率，本实验使用信息增益特征选择方法[14]来选择区分异常与正常流量中信息量最高的13 个特征属性，见表1。

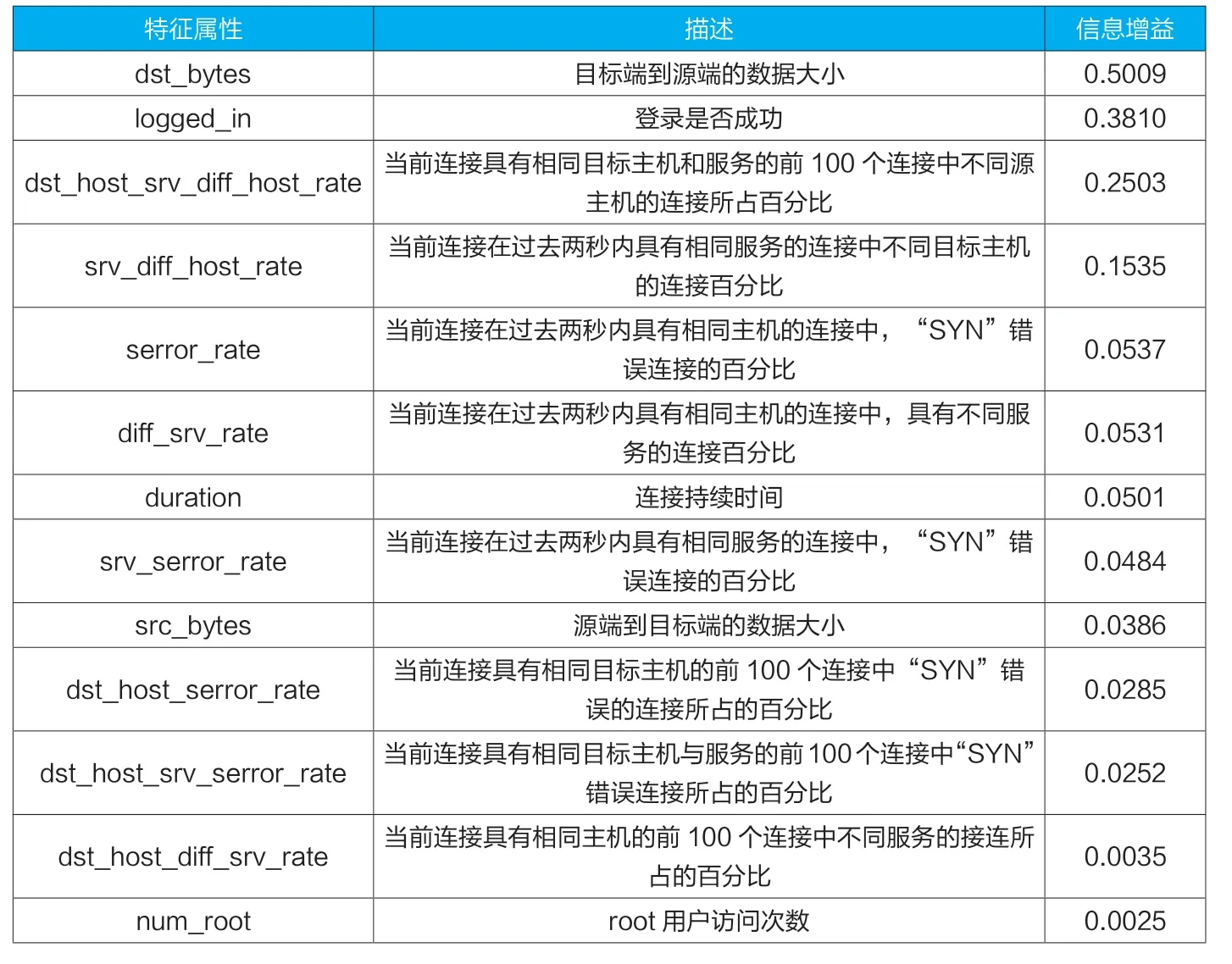
表1 特征属性说明与信息增益值

数据预处理完了之后，进行多级优化BP 神经网络模型的训练。根据本实验选择的特征设定的BP 神经网络模型的参数：输入层神经元和隐含层神经元都为13个，输出层神经元为1 个。ABC 算法模型的参数：初始化蜂群为60、迭代次数为100。PSO 算法模型的参数：粒子群大小为40，迭代次数为50，惯性因子为0.8，局部学习因子与全局学习因子都为2。然后对BP神经网络、ABC 优化BP 神经网络和多级优化BP 神经网络做收敛效果和准确度的评估对比实验。

收敛效果评估

收敛效果是评估模型的重要指标。从处理过后的数据集中随机选择2000 条数据作为训练集进行训练误差的收敛对比分析。经过实验仿真后的收敛结果如图2 所示。

图 2 算法误差收敛图

从图2 可知，如果设定训练误差为，ABC 和PSO 多级优化BP 神经网络的模型在迭代500 多次的时候就满足了误差的要求，其他两种算法在相同迭代次数下，均未达到设定的误差要求，需要继续迭代。因为BP 神经网络初始化时权值和阈值是在自定义的范围内随机产生，通过反向传播调整时只能在随机数的附近调整，容易陷入局部最优，缺乏全局最优的考虑。当使用ABC 算法一级优化BP 神经网络时收敛速度得到了较大的提升，在达到迭代要求时，由于算法没有依据先验信息进行角色转化和重新初始化食物源，缺乏对当前最优解的考虑，导致模型后期迭代速度变慢。但是使用ABC 和PSO 算法多级优化BP神经网络时，PSO算法既考虑局部最优，又能快速全局搜索，进而减少了无效的迭代次数。因此，证明多级优化BP 神经网络模型具有更快的收敛速度，使异常检测的效率得到更大的提升。

准确度评估

将处理过后的数据集随机分布后作为训练集和测试集，然后选择K 折交叉验证方法来计算数据的正确率，其中K 折交叉验证的参数K 取值为10。在异常检测中为解决数据不平衡带来指标评估的不良影响，本文建立混淆矩阵来验证实验模型[15]。样本测试数据中的检测异常流量、检测正常流量分别由矩阵中的TP（True Positive）和TN（True Negative）表示，识别错误的异常流量和正常流量分别由FN(False Negative)、FP（False Positive）表示，具体见表2。

表2 混淆矩阵

对异常检测模型的结果评估主要包括准确率（Precision Rate，PR）、误报率（False Positive Rate，FPR）、漏报率（False Negative Rate，FNR）等评价指标。各指标的定义如下公式所示。

1.准确率PR 的计算公式如式（11）所示，

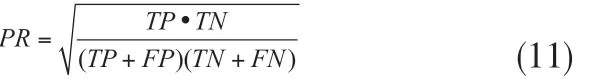
2.误报率FPR 的计算公式如式（12）所示，

3.漏报率FNP 的计算公式如式（13）所示，

通过混淆矩阵计算，各模型的准确率比较情况见表3。

表3 模型准确率比较

从表中的数据可以看出，ABC 和PSO多级优化BP 神经网络模型在异常流量检测中的检测效率更高。传统BP 神经网络模型在满足误差要求时就会结束，最终得到的参数可能不是全局最优，使异常流量检测模型的效率不理想。但是ABC 和PSO 多级优化的BP 神经网络模型经过快速的全局搜索，使异常检测的正确率、误报和漏报率都有更好的优化。

未来研究

使用神经网络的方法对网络异常流量的检测是网络安全方面研究的重点课题。本文使用人工蜂群和粒子群结合算法来优化BP 神经网络的权值和阈值，克服了BP神经网络易陷入局部最优、收敛速度慢等问题。通过在异常流量检测中的应用发现该算法降低异常检测时较高的误报和漏报率并提升了检测准确率，从而证明该优化算法的可行性。但是没有针对不同的数据集进行测试并智能化的应用到实际中，因此还有需要进一步的完善，以后研究可以考虑多级优化BP 神经网络有限的泛化能力或者采用深度学习技术进行异常流量检测分析。