大规模联合平差中的方差分量估计并行设计

李 庆，刘 增

（信息工程大学，郑州 450001）

1 引言

在大规模GNSS观测网进行独立网平差及与其它观测网进行联合平差的过程中，一般根据测量条件的不同将整网分成若干子网，各子网先进行单独平差消除子网内部以及子网之间的粗差［1，2］，而后是子网间的系统性差异。系统性差异体现在函数特性和随机特性两个方面，消除随机特性的系统性差异通常采用方差分量估计的方法。方差分量估计需要大量法方程系数矩阵求逆和矩阵相乘计算，传统联合平差中的方差分量估计效率将会非常低。为提高传统网平差解算效率，对于高性能计算技术的研究成了近几年的热点，由于高性能计算技术的本质是并行计算，将传统的GNSS数据处理模型分解并设计合理的并行算法是实现GNSS数据快速处理的首要问题［3］。

本文基于方差分量估计原理和以任务划分为基本模式的并行算法，结合已有的大型矩阵高效计算方法，设计了大型联合平差中的并行方差分量估计的基本流程，理论上提高了硬件资源的利用率和参数估计效率。

2 方差分量估计原理

平差的数学模型包括函数模型和随机模型，函数模型是描述平差问题中观测量与观测量之间、观测量与未知参数之间相互关系的函数表达式，随机模型是描述观测误差的一些随机特征，在平差中主要指观测值的数学期望和方差［4］。虽然观测值的权可以由一些经验公式确定，但往往不具备普适性，所以常采用对随机模型进行验后估计的方法。随机模型的验后估计，其基本思想是先对各类观测量定初权、进行预平差、利用预平差后得到的信息、主要是各类观测值的改正数V，依据一定的原则对各类观测值的验前方差和协方差作出估计，依此定权［5］。方差分量估计是利用验后方差重新定权的，最常用的是Helmert方差分量估计法。对于k类观测量相互独立的情况，有严密公式得到相应的方差分量估值［1］：

②平差求出第一次参数估值和残差；

3 并行设计相关

设计并行的第一步就是将问题分解成多个任务。一个任务是一个指令序列，并且作为一个小组一起操作，这个小组相当于一个算法或者程序的某个逻辑部分［6］。即任务的划分体现了算法设计者对问题的思考。但是任务和执行线程绝不是一对一的关系。如对于k类观测量的k个系数矩阵Ai、自由项矩阵li、权矩阵Pi分别建立的法方程法矩阵Ni=和法向量Ui=A将每一个建立过程视为一个任务执行，并不会需要k个线程同时运行。因为每类观测量的观测个数各不相同，相应所需的任务时间花费也不相同。现阶段基于任务的编程方法考虑的主要是任务调度中负载平衡的问题。负载平衡（Loadbalance），即指有效地在各处理单元间分配任务，当一个设计能够平衡处理单元间的计算负载时，它的执行效率要高于处理单元间计算负载不平衡的情况［6］。获得一个最佳动态调度可以采取工作窃取 （work stealing）的策略，在任务执行开始时，把任务分布到各个线程上，每一个线程有自己的工作队列。当工作队列为空时，线程将随机从其它线程的任务队列中窃取工作，如图1所示。

图1中，6个待执行的任务通过4个线程并行执行完成。若串行运行任务，完成的总时间等于6个任务分别执行的时间之和，而采取并行执行的方式，完成的总时间仅为任务E执行的时间，大大提高了任务执行效率。任务调度器会自动根据所有可用的逻辑内核尝试对任务进行负载均衡，在幕后使用工作窃取队列找到一个最合适的线程，并将任务加入队列中［3］，避免出现部分线程执行大多数任务而其它线程处于闲置状态的情况。

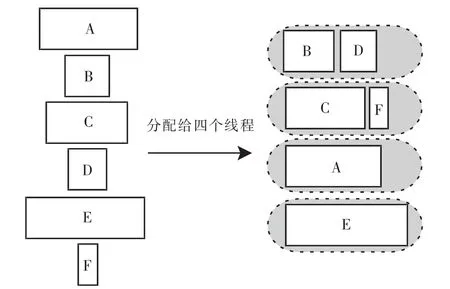
图1 串行、并行比较

4 联合平差中的方差分量估计并行设计

①联合平差的观测量被分成了k类，我们把这k类相互独立的观测量的初始信息保存在k个不同的文件中，包括每一类观测量的系数矩阵Ai、含有坐标近似值的自由项矩阵li、由单独平差或经验公式得到的初始权矩阵Pi以及该类观测量的观测总数mi。基于并行处理的思想，划分k个任务，并行读取每类观测量的初始信息，并计算法方程系数矩阵Ni=和法向量Ui=

②对各个任务组的法方程系数矩阵Ni和法向量Ui进行总法方程的并行累加计算，得到联合平差的总法方程系数矩阵N和法向量U。

③第三步的计算有两种方案。方案一：划分k个任务，利用缓存的各类观测量的法方程信息，并行组成法方程，解算参数和需要的残差向量Vi；方案二：直接利用第二步得到的总法方程系数矩阵和法向量结果，组成法方程，解算总的残差向量V，其分量即为所需要的各类观测量的残差向量。两种方案在解算法方程时，都涉及大型矩阵的相乘和求逆，可以采用文献［7］研究的并行矩阵分块乘法和法方程系数矩阵的Cholesky分块分解并行求逆方法，不仅可降低存储对内存的要求，也有效提高了计算效率。

⑤按方差分量估计解算方差估值分量的公式分别在k个任务里组成方程，利用这k个任务返回的结果并行解算方程组。由于观测量分类个数k不会太大，故解这k个方程对整体解算效率影响不大。