基于改进离散事件系统的测试性建模方法∗
2019-02-27吕鑫燚吕晓峰孙艺靓
叶 文 吕鑫燚 吕晓峰,2 马 羚 孙艺靓
(1.海军航空大学 烟台 264001)(2.西北工业大学电子信息学院 西安 710072)
1 引言
离散事件系统(Discrete Event System,DES)是20世纪80年代提出的一类在时间上和空间上都是离散的人造系统模型,该理论一经提出便得到广泛应用与发展,特别是在铁路系统、通讯系统、控制系统等方面[1]。
由于数模混合电路具备DES的两个关键特征[2],因而DES可被应用于芯片级、板级电路的测试性建模与分析的研究。但是由于其测试性建模的信号流反馈环过多,因而存在故障的关联性过多而难以有效区分的问题,进而造成其建模的计算复杂程度比较高,建模过程复杂的弊端。
而现有的测试性建模方法中,相关性模型是一种较为有效的建模方法,它考虑系统测试与诊断过程中的测试与部件之间的因果连接关系,并采用有向图的形式描述这些关系,使模型不仅描述直观,而且建模难度低[3~4]。
因此,本文针对基于DES的测试性建模过程复杂的问题,借鉴相关性模型建模方法[5],将故障与测试相关性矩阵引入到基于DES的测试性建模中,以提高建模效率、简化建模过程,最后通过建模实例评估该测试性建模方法的效果。
2 基于改进离散事件系统的测试性建模
基于离散事件系统的测试性建模主要从故障状态与测试之间的相关关系着手,建立其相关性矩阵。由于DES理论从电路的基本故障状态出发,因此很适合于元器件级的测试性建模,其测试性模型如图1所示。
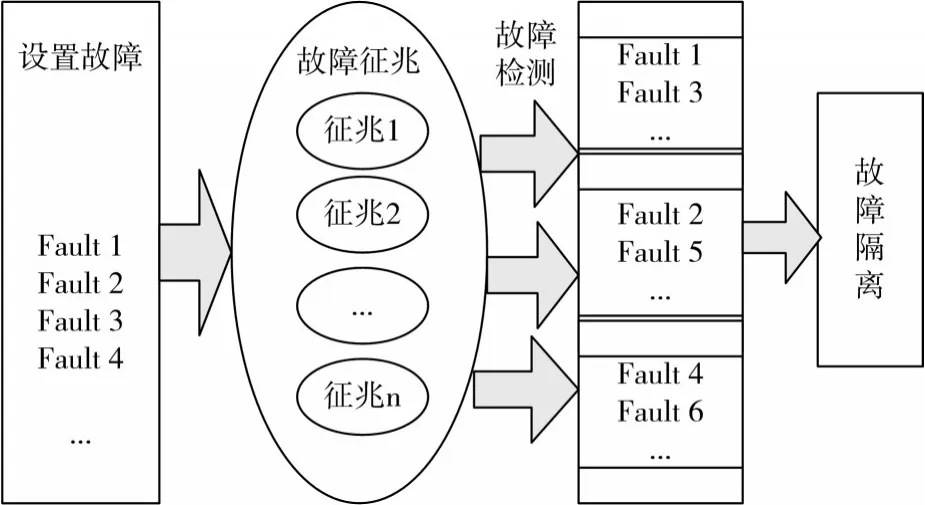
图1 DES测试性模型
基于DES的测试性建模中,离散事件用于描述测试结果,离散状态用于描述元件的故障状态。对电路G进行测试性建模[6]如式(1)所示

其中,Σ表示电路G的全部可观测离散事件集合;Q表示电路G的全部故障状态集合;δ:Σ*Q→2Q为转移函数,主要描述离散事件与故障状态间的相关关系。
基于传统DES的测试性建模过程极其复杂,且针对该模型的故障诊断算法速度慢、精度低,后续测试性分析的难度也随之提升。因此本文借鉴相关性模型建模方法,将故障与测试相关性矩阵引入到基于DES的测试性建模中,形成基于改进DES的测试性建模方法。即通过建立故障状态与测试事件的相关性矩阵,简化复杂的建模过程以提高建模效率,同时为后续测试优化选择和诊断策略分析提供有力的数据基础。
基于改进DES的芯片级、板级电路测试性建模流程如图2所示。
具体的建模步骤如下:
1)分析故障信息,设置有限的故障状态集合Q;
2)选择可用测试集,设置有限的测试事件集合Σ;

图2 基于改进DES的测试性建模流程
3)通过EDA软件对电路进行仿真实验,根据实验结果建立有限故障状态集Q与测试事件集Σ的驱动关系列表,其中可观测事件δ:Σ*Q→2Q描述了测试事件与故障状态之间的关系;
4)建立故障-测试相关性矩阵D,为下一步测试性分析奠定基础。
3 建模实例
本节将通过2个建模实例展示具体的建模步骤,以验证本文方法的有效性和实用性。
实例1:以图3所示的某滤波电路为例,该电路参 数 设 置 如 下 : R6=160Ω,C1=0.1μF,R4=R5=10Ω,R7=2R8=20KΩ,C3=2C2=20nF。图中Ui为信号输入端,TP1和TP2为测试节点。

图3 滤波电路
第一步,对滤波电路进行故障分析,本文以偏离标称值20%表示发生了参数性故障,建立故障状态集Q={ f0,f1…,f18} ,其中,f0表示正常工作状态,f1~f18表示电路中的故障状态,具体设置如表2所示。
第二步,在Ui端输入幅值为1.5V的方波信号,取在测试点测得的输出电压为测试事件集Σ={T1,T2…,T8} ,具体设置如表1所示。
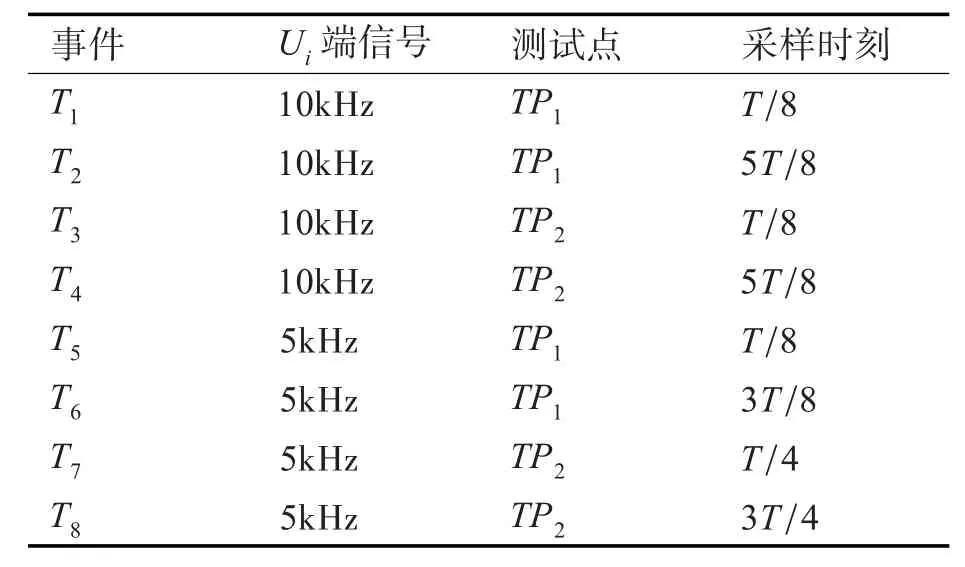
表1 滤波电路测试事件集
第三步,通过EDA软件Pspice得到该电路的仿真测试结果如表2所示。依据故障状态 f1~f18与测试事件T1~T8的相关关系建立测试事件集与故障状态集的驱动关系列表。将仿真中采集的电压值和标准电压值相减即可得到可观测事件集δ={t1, t2…,t16} ,其 中 t1=T1-1.642>ε,t2=T1-1.642<-ε,t3=T2-1.344>ε,t4=T2-1.344<-ε,…,t16=T8-1.328<-ε,本文取 ε=0.09V。

表2 滤波电路EDA仿真
最后,依据可观测事件成立则矩阵中对应元素为“1”,反之为“0”的规则,得到滤波电路的故障-测试相关性矩阵如表3所示。

表3 滤波电路的相关性矩阵
实例2:以某型导弹发控通道中的战术发射电路为例,阐述应用本文方法的建模过程,该电路的仿真图及测点设置如图4所示。
根据文中方法分步建立该电路的测试性模型。第一步,对战术发射电路进行故障分析,建立故障状态集Q={ f0,f1…,f25} ,具体设置如表 4 所示。

表4 故障状态集
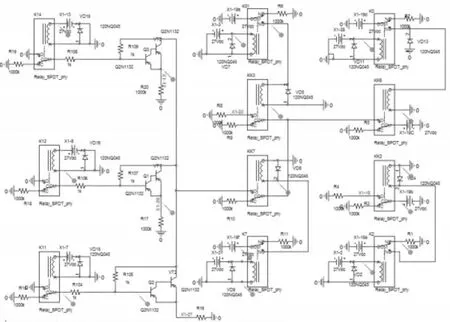
图4 战术发射电路仿真电路图

表5 战术发射电路EDA仿真
第三步,通过EDA(Electronic Design Automation)软件Pspice得到该电路的仿真测试结果如表5所示。依据此表建立测试事件集Σ与故障状态集Q的驱动关系列表。取仿真中采集的电压值和标准电压值得绝对值即可得到可观测事件集δ={t1, t2…,t18} ,其中t1= | T1-27 |> ε,t2= | T2-0 |> ε,t3= | T3-26.866|>ε,…,t18= | T18-27|>ε,本文取ε=0.7V,即二极管的导通电压[7]。
最后,依据可观测事件成立则矩阵中对应元素为“1”,反之为“0”的规则,得到战术发射电路的故障-测试相关性矩阵如表6所示。
通过分析相关矩阵可得到测试性指标,为后续测试性设计中的测试优化选择和诊断策略设计提供理论基础。
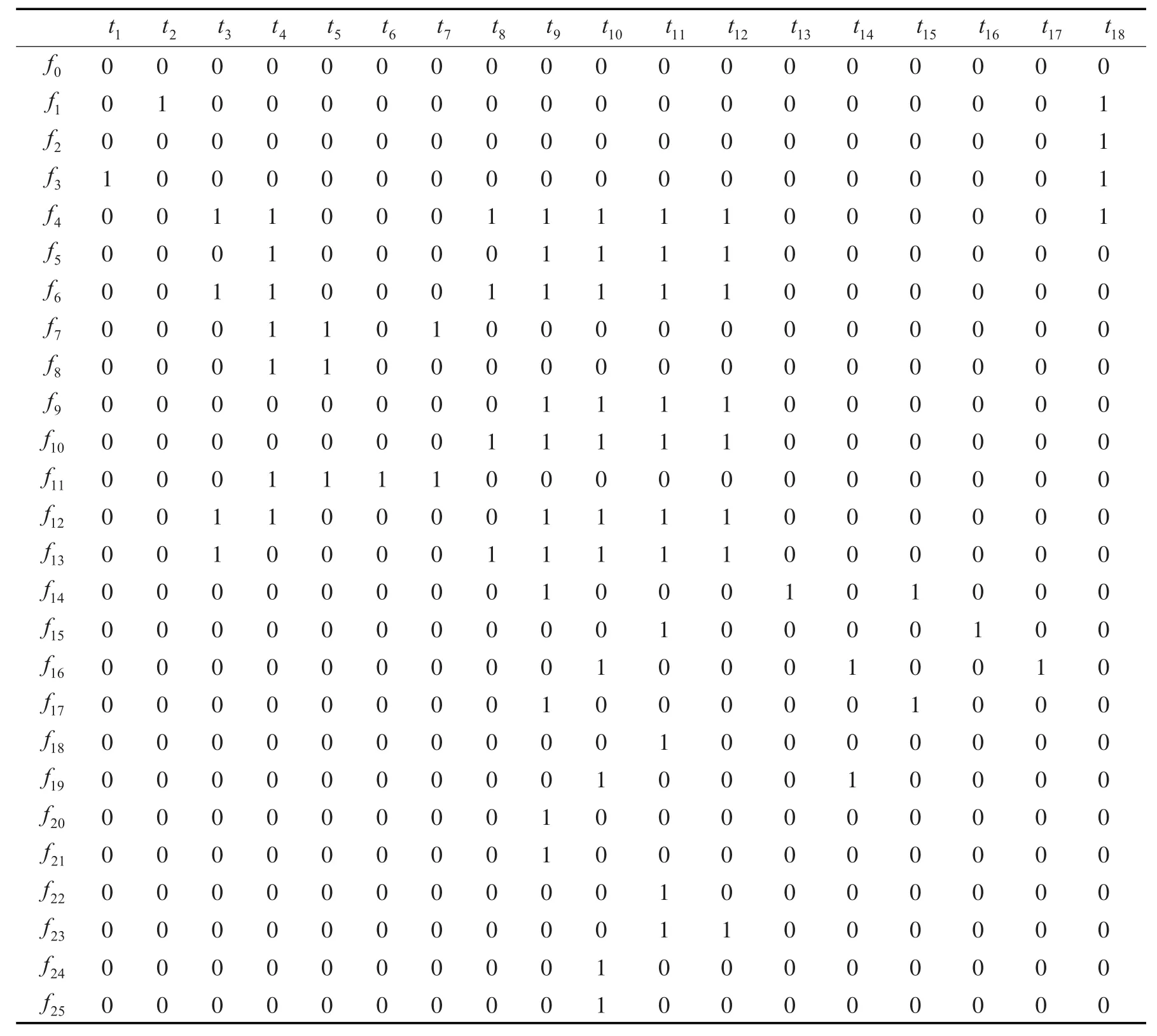
表6 战术发射电路的相关性矩阵
4 结语
针对现有基于离散事件系统测试性建模过程繁琐的问题,提出了一种改进的测试性建模方法。该建模方法结合基于DES的测试性建模和相关性模型的优点,将故障-测试相关性矩阵借鉴到基于DES的测试性建模中并对其进行改进,从而建立针对芯片级、板级电路的直观高效测试性建模方法。最后通过建模实例验证了本文提出的改进建模方法的实用性和有效性,为进一步研究测试优化选择和诊断策略优化方法提供了理论基础。
