水下航行器总线控制网络的数据传输失效率理论研究∗

杜晓海 李凯凯

（1.海军装备部 西安 710065）（2.西北机电工程研究所 咸阳 712099）

1 引言

在水下航行器武器装备中，网络控制系统扮演着非常重要的角色。在工业控制、汽车电子、航空航天以及远程监测系统等领域中都有着广泛的应用［1～4］。在网络控制系统中，不同节点之间交互的报文可以分为两大类：一类称为非实时报文，这类报文在节点间的交互延时不影响整个网络运行的可靠性；另一类称为实时报文，实时报文的交互延迟需要满足一定的条件，即延迟应小于给定的死限，否则将导致网络中不可预测行为的发生，乃至整个网络崩溃。显而易见，报文的实时性是保证整个网络可靠性的重要因素。在网络控制系统中，报文的实时性主要由三个参数决定：报文的产生时间、阻塞时间以及传输时间。由于网络媒体接入控制协议和节点软件架构的原因，上述三个参数通常都是随机变量。这些随机变量和网络控制系统可靠性之间的联系已成为众多学者关心的一个问题［3～4］。然而，目前的研究工作中通常都是在上述随机变量的分布规律完全已知的情况下进行的。然而，在实际网络控制系统的分析过程中，报文的产生时间、阻塞时间以及传输时间都是借助特定测试设备进行一定时间的实验后测量得出的，因而通常只能给出这些随机变量的部分统计量（如均值、方差）的置信区间。换句话说，这些随机变量的信息对于网络设计人员来说是不完备的。这种情况下对报文传输失效率（Failure Probability，FP）下限的精确估计就显得尤为重要，因为这是决定整个网络报文传输最高可靠度的水平。本文研究了在信息不完备情况下网络控制系统报文传输失效率下限的计算问题，推导出了报文传输失效率下界的解析公式。利用Vector公司的网络测试设备VN7600，对一个实际的水下航行器CAN总线网络中报文的传输延迟进行了测量，实验结果证实了解析公式的正确性。本文的理论结果对于网络控制系统的可靠性准确评估和预测有一定的参考价值。

2 网络控制系统报文传输失效率的数学模型

2.1 报文传输时间模型

在网络控制系统中，由于节点媒体接入访问控制方式、网络带宽限制、网络负载变化的随机涨落以及节点数据处理延时等因素的制约，节点之间的报文通信延迟可用下图所示的传输模型来表示［3］。

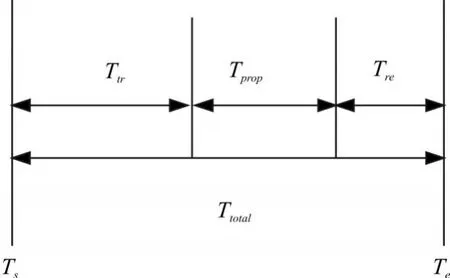
图1 网络控制系统报文传输时间模型

如图1所示，在网络中信息的发送和接收是以报文为单位完成的。报文总的传输延迟Ttotal定义为从源节点欲开始发送报文时刻Ts开始，到目的节点完成整个报文的接收时刻Te为止。其中包含三个部分：报文在源节点发送的总延时Ttr、报文在网络上的传输延时Tprop以及目的节点接收报文所需的延时Tre。从更为普遍的情况来分析，报文在网络中的传输延时Tprop和目的节点接收报文所用延时Tre都比较小，而且其数值大小也基本是确定不变的。因此，在本文后面的分析中将这两个量忽略不计。而源节点发送报文的总延时Ttr又由三个部分组成：报文的阻塞时间Tb、将一条完整报文一次性成功发送至网络的时间Tframe以及源节点中的软件处理延时Ts。阻塞时间Tb由网络中媒体接入控制机制决定，是影响网络性能的主要参数。Tframe主要由报文的长度（以比特为单位）和网络的位时间（即发送1个比特需要的时间）确定。源节点中的软件处理延时Ts则是由源节点的处理器主频、指令系统以及软件体系架构等方面共同决定的。这样总的传输延迟可以表示为

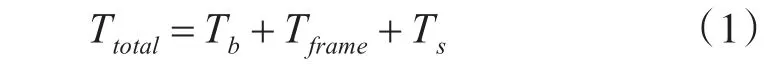
2.2 网络控制系统报文传输失效率模型

一般意义下可靠性被定义为：一个系统在规定条件下和规定的时间内完成规定任务的能力。在网络控制系统中，如果实时报文不能在规定的截止期内完成传输将会对网络造成巨大危害甚至导致系统崩溃。因此，网络控制系统中报文传输的可靠度可以用下面的状态函数来刻画：

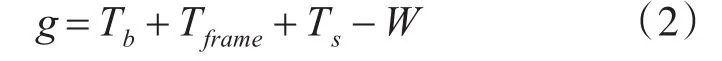
其中W表示报文传输的截止期。若g≤0则表示报文传输成功，网络正常运行；若g＞0则表示报文传输失败，网络出错。由于在式（2）中右侧的三个量Tb、Tframe和Ts均是随机变量，网络控制系统的可靠性可以用网络的失效率Pf来表示：

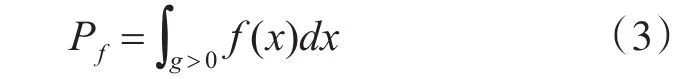
其中 x=(Tb，Tframe，Ts)为随机参数向量，f(x)为该随机向量的联合分布密度函数。显然，Pf的大小是网络控制系统的设计人员所关心的问题。尤其是Tb、Tframe和Ts等参数与Pf的关系，更为研究人员所关注。下面我们将重点分析在信息不完备条件下Pf的主要性质。

3 网络控制系统报文传输失效率（FP）的下界

在概率和信息理论中，交叉熵可以用于度量两个随机变量概率分布差异的大小。其定义为［5］

其中p和q表示两个不同的概率分布函数，S为随机变量p和q的取值空间。相对熵的定义中要求p与q绝对连续，否则R(p||q)=∞。同时，相对熵R(p||q)满足非负性条件，即 R(p||q)≥0，当且仅当p=q时R(p||q)=0。

从式（2）可知，网络控制系统失效率Pf和三个随机变量Tb、Tframe和Ts相关。若这三个随机变量的概率分布完全可知，则失效率Pf的大小也可以唯一地确定。当上述随机变量的概率分布规律存在信息不完备的时候，则Pf的数值也不能被唯一确定。此时我们更加关心Pf在“最坏情况”下数值。从数学的角度来看，需要求出Pf的下界。通常可以采用蒙特卡洛方法进行数值计算。然而蒙特卡洛法需要较多的取样次数才可以得到稳定的结果，故而计算效率不高。同时数值计算的结果也不能直观反映不同参数对报文传输失效率下界的影响。这里，我们尝试推导出Pf下界的解析结果。

为分析方便，首先建立所述问题的符号系统。本文中用三元组(Ω，F，P)表示概率空间，其中Ω为基本事件空间，F为Ω上的σ代数，P为(Ω，F)上的概率测度。P(Ω)表示(Ω，F)上所有概率测度的集合。令 x=(Tb，Tframe，Ts)为一个定义在 (Ω，F)上的3维随机变量，其概率分布函数为 p(x)。用该3维随机变量可以定义某网络控制系统报文传输的失效率Pf：

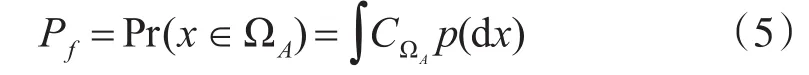
其中ΩA⊂Ω表示网络系统失效的取值区域，CΩA表示ΩA的特征函数，其定义为

而ΩA可以用状态函数g(x)来描述：

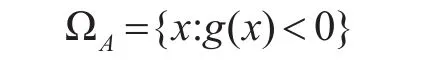
在本文研究的网络控制系统中，x是一个三维随机变量 (Tb，Tframe，T)s，状态函数 g(x)则由式（2）定义。

假设(Ω，F，P)表示概率空间，h是一个Ω→ℜ的有界可测函数，p∈P(Ω)。根据文献［5］给出的一个关于交叉熵的变分公式：

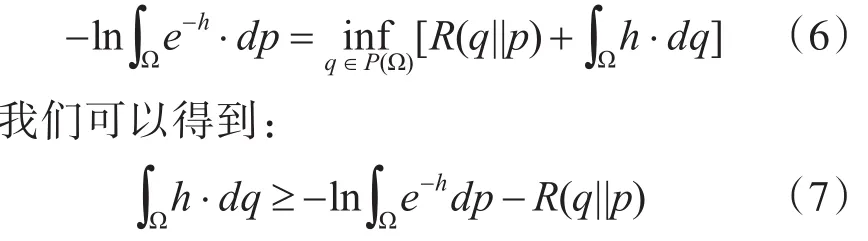
分析式（7），该不等式成立的条件中只规定了h是一个Ω→ℜ的有界可测函数。回顾前面的描述，ΩA的特征函数CΩA正好满足上面的条件。不失一般性，将函数h的具体形式定义为h=aCΩA（a＞0）。于是可得下式：

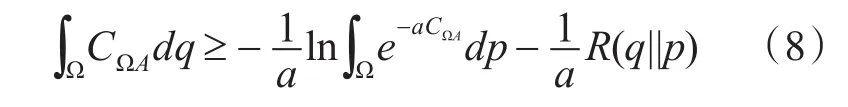
其中 a∈(0，∞)。

由于 q∈P(Ω)，因此式（8）表明失效率 Pf的下界由下式给出，其中sup表示函数的上确界。

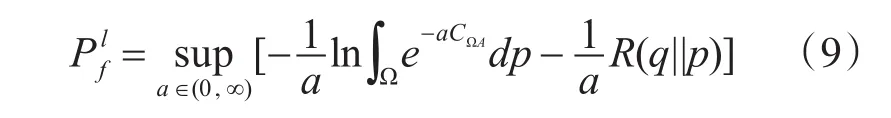
分析式（9），其中右侧的因子R(q||p)与a无关，为此可将其简化为下式：

这样，在信息不完备条件下整个网络控制系统的失效率的下界可以用式（10）来表示。在本文后面的讨论中，我们将信息不完备的条件限制在一个较为常见的范围内：即随机变量的分布函数是确定的，其中的一个或多个统计量（如均值、方差等）的具体取值不确定，其取值的区间是已知的。同时，在具体问题的分析中，都存在一个最接近真实分布的分布函数，我们称之为“标准分布”。在式（10）中的p即可以表示“标准分布”。在这种情况下，由于p和q的数学形式可知，Rsup一般可以通过解析的方式得到。

式（10）尽管给出了确定失效率下界的公式，但可以看出这需要经过一个单参数的优化过程，即需要寻找下界对应的a的数值。我们尝试推导解析计算式（10）的方法。分析式（10）中的 F1(a)，其被积函数中都包含一个因子eaCΩA，根据ΩA的特征函数CΩA的定义，不难得到

其中P1分别表示随机变量服从“标准分布”函数p时系统的失效率，而P2=1-P1。将上面的结果代入式（11）中，并且对其和进行求导，可得

式（13）即为网络控制系统报文传输失效率的下限对应的a的隐式解析解。

4 实验分析

本文中我们采用Vector公司的VN7600网络测试工具，对一个实际的水下航行器CAN总线网络中的报文进行了实时测试。该网络中包含5个节点，共有10个报文，实验中连续对这10个报文的传输情况进行了连续40个小时的测试。图2所示为实验测试得到的10个报文传输失效率和用解析结果式（10）计算所得的失效率下界。

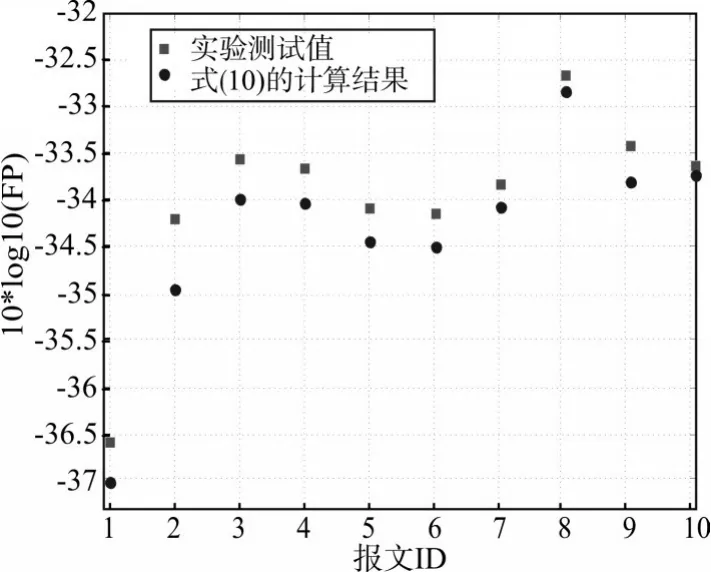
图2 传输失效率和失效率下界

图2 中，实验测试得到的报文传输失效率的结果用方框表示，用式（10）计算得到的失效率下限用圆圈表示。图中报文失效率采用对数坐标表示。可以看出，本文理论计算的报文传输失效率下限都比实际报文传输失效率小，证明了理论结果的合理性。另一方面，从图中还可以看出实际报文的失效率与理论预测的失效率下限差别并不大。换言之，在信息不完备条件下理论预测的失效率下限的“比较有效”。在网络控制系统的设计或分析阶段，本文结果对系统可靠评估能提供一种有效的依据。

5 结语

本文研究了水下航行器网络控制系统中实时报文传输失效率的问题。从交叉熵的变分公式出发推导出了在信息不完备条件下网络控制系统报文传输失效率下限的解析公式。利用Vector公司的网络分析工具VN7600，对一个实际的水下航行器CAN总线网络的报文传输参数进行了测试，实验结果证实了解析公式的准确性和有效性。本文的理论结果为水下航行器网络控制系统的性能分析和优化设计提供了一种有效的方法。