基于快速正交搜索算法的被动声纳浮标目标方位估计∗

吴 双 刘 珏 刘本奇

（1.上海船舶电子设备研究所 上海 201108）（2.水声对抗技术国防科技重点实验室 上海 201108）

1 引言

声纳浮标是固定翼反潜飞机和反潜直升机装备的一种非常重要的反潜设备［1］。作战时，反潜飞机沿搜潜航路投放一定阵型的声纳浮标，进行水文探测和对周边潜艇信号的收集［2～3］。按工作方式可分为主动式声纳浮标和被动式声纳浮标；按定向方式可分为定向式声纳浮标和非定向（全向）式声纳浮标。

DIFAR浮标是一种被动定向声纳浮标，它由全向通道和两个相互正交的正弦、余弦通道组成。图1为DIFAR浮标水下部分纵向截面的示意图，全向弯曲晶片是全向声压水听器的组成部分，安装在水听器底部，用来测量任意来向入射声波的声压幅值，构成全向通道；DIFAR浮标中有两个相互垂直摇摆臂，每个臂上有两个陶瓷晶片，构成一个声振速传感器，每个声振速传感器包含两个陶瓷晶片，呈偶极子排列，故形成了正弦、余弦两个通道［4］。由于浮标在水中的方向是随机的，故它还包含一个罗盘用来感知自身方向。浮标在水中还会产生自转，需要罗盘对传感器检测的目标方位进行纠正。

DIFAR浮标通常采用FFT/B-Scan法进行目标方位估计，该方法通过对每个通道的数据进行傅里叶变换，采用反正切计算就可以得到目标的方位估计，因为该方法是基于FFT的，故它有一个很明显的缺点就是当两个目标的频率靠的很近时（FFT无法区分这两个频率），无法准确地对接收到的信号进行方位估计，而FOS算法就能有效地解决这一问题。

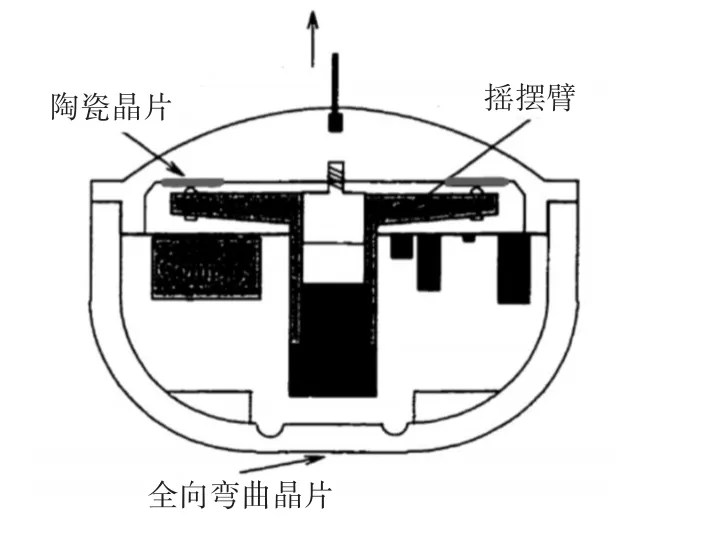
图1 DIFAR浮标水下接收部分纵向截面示意图

2 FFT/B-Scan算法

图2给出了DIFAR浮标水听器偶极子结构。假设在角度θ有一声源，三个水听器的输出分别为

其中下标o、s、c分别代表全向通道、正弦通道和余弦通道。no(t)、ns(t)、nc(t)是各通道的噪声，对上述三个通道的输出信号求其互功率谱密度，进而求得入射方位角θ。

图2 DIFAR浮标三个水听器的几何学结构［5］

对信号x(t)作离散傅里叶变换：

即三个通道的信号xo(k)、xs(k)、xc(k)分别进行DFT得到 Xo(k)、Xs(k)、Xc(k)。通过下式可求得功率谱密度（PSD）：

上式中“*”代表复共轭。得到各个通道的功率谱估计分别为

类似的各通道的互功率谱密度为

从上式可以很明显地看出，要想求得目标声源方位，只需通过下面一个简单的三角关系式即可：

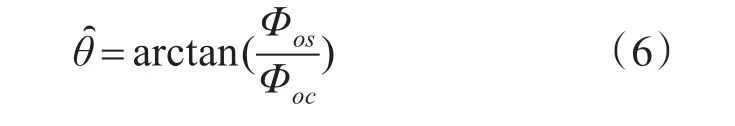
θ̑即为目标声源的方位估计值，介于0～2π之间。

3 FOS算法

快速正交搜索（Fast Orthogonal Search，FOS）算法能够最大限度地减小估计量相对于目标数据的均方误差［6］。该算法的实现是在所有的候选函数中选择基函数，能使均方误差的减小量最大的候选函数被确定为基函数，并从候选函数中移除；在剩余的候选函数中重复上述选择过程，直到满足相应的停止条件时结束选择［7］。目前，FOS算法已经有了很多的实际应用，包括递归滤波去除图像中的高斯噪声和脉冲噪声，语音信号的压缩，磁共振成像和正电子发射断层扫描以及非线性系统的控制和基因的识别等［8］。

当然，FOS算法也被应用到了谱估计和时频分析中。该算法用任意一组非正交候选函数 pm(n)来表示输入函数y(n)，并且通过对 pm(n)的筛选来使输入函数y(n)和用非正交候选函数表示的函数展开式之间的均方差（MSE）最小［12］。

输入函数y(n)的展开表达式为

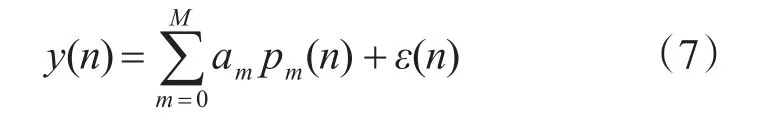
其中，am为函数展开式的相应权值，ε(n)为模型误差。由于非正交候选函数 pm(n)可以任意选取，则式（1）的表达形式不唯一［9］。故选取一组正交基底函数来构造新的函数展开式：

其中，wm(n)为选取的正交基底函数，gm为相应权值，e(n)为误差项。式（9）中的上划线代表从n=0到n=N-1的时间平均，即 。 wm(n)是利用格拉姆-施密特（Gram-Schmidt）正交法［10］将非正交候选函数 pm(n)正交化后得到的两两正交的函数序列。在正交化的过程中，会求得两组正交系数αmr和权值系数gm，通过这两组系数最后就可求得系数。

FOS搜索算法进行谱分析，通常选取成对的正弦和余弦函数项为候选函数 pm(n)，假设第一项为直流项（m=0），则：

那么，式（7）可以表示为

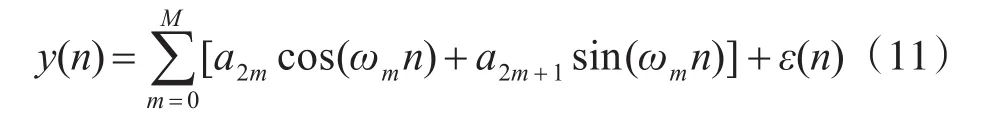
其中，m=1，…，M，ωm是对奈奎斯特频率归一化后的候选函数对的数字角频率，M是候选函数对的个数，a2m和a2m+1为三角函数幅值。

通过对每个候选频率选取合适的三角函数对，该频率所对应的相位和幅值也随之确定，如下所示：

4 仿真分析

假设目标声源由一组正弦信号组成，即

由式（1）可得，DIFAR三通道接收到的信号分别为

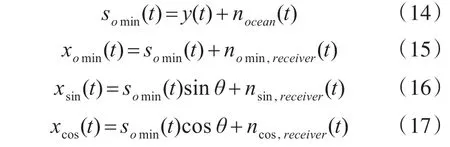
其中，nocean(t)是海洋环境噪声，nomin，receiver(t)、nsin，receiver(t)和 ncos，receiver(t)分别为三个通道的通道噪声。海洋环境噪声对三个通道的影响是一样的，而接收端的通道噪声是相互独立的。

本文假设目标声源由101Hz和100Hz两个频点组成，幅值A=［1 2］，信号相位φ=［0°45°］，目标声源入射方位θ=［60°120°］。海洋环境噪声为加性高斯白噪声，忽略通道噪声。数据长度T=1s，采样频率1.25kHz。

图3是信噪比在-5dB时，基于FFT的B-Scan方位估计和基于FOS的B-Scan方位估计。

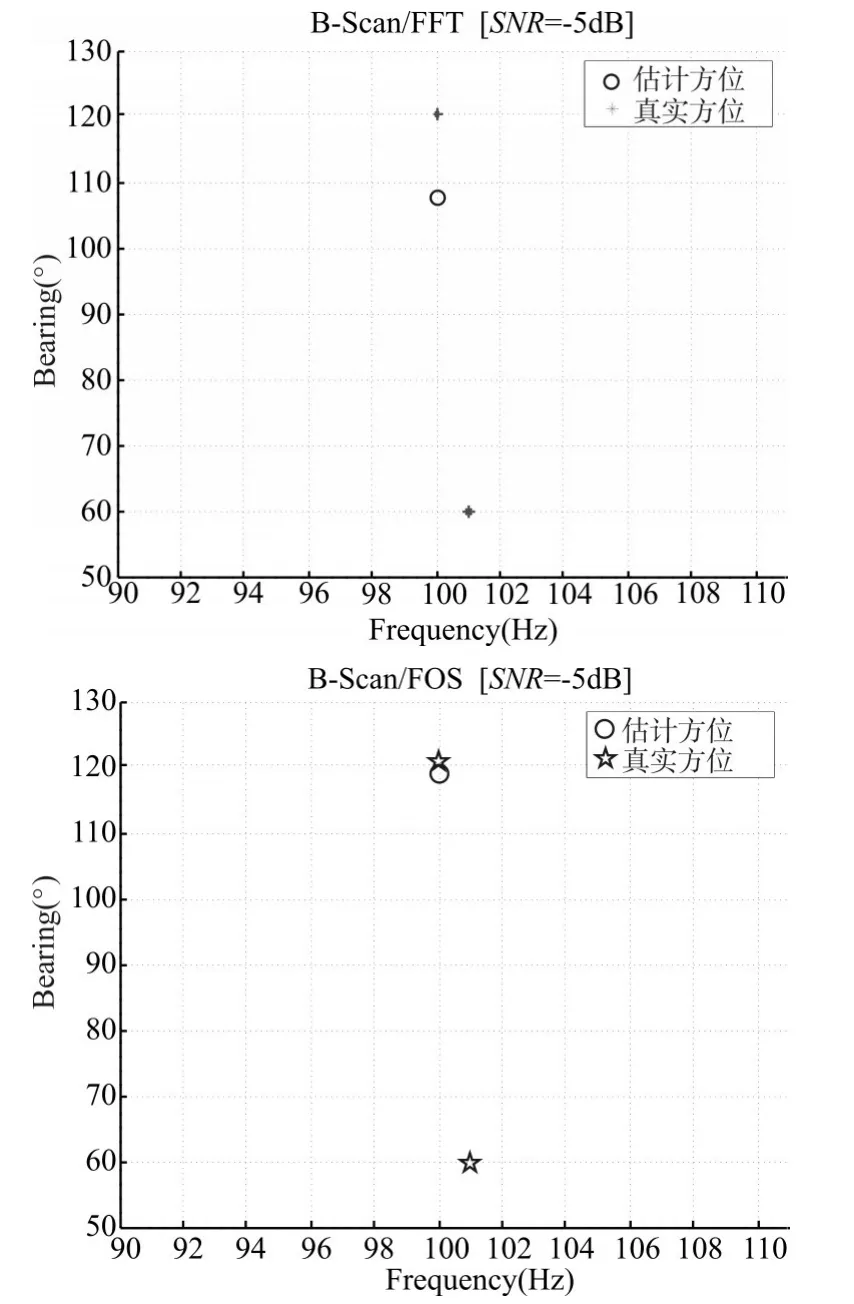
图3 T=1s时FFT和FOS算法的B-Scan图

从图3中可以很明显地看出，FOS/B-Scan算法准确地估计出了目标的方位和频率点，而FFT/B-Scan算法则很明显效果差很多，不仅目标方位没有估计准确，更重要的是目标个数同样没有估计准确，仅估计出一个目标的频率信息。表1是不同信噪比下，以上两种算法对频率和方位角估计的结果对比。

从表1中可以清楚地看到，在-9dB～9dB之间，不论信噪比为多少，FFT/B-Scan算法都无法准确地估计出两目标的频率和方位角，而FOS/B-Scan算法无一例外都能准确地估计出目标。以上过程在进行功率谱估计时，为了改进其方差特性，将数据平均分为5段且每段无重叠，分别求每一段的功率谱，然后加以平均。FFT/B-Scan算法之所以会出现这种情况是因为，此时FFT算法的分辨率为5Hz，而两目标的频率间隔为1Hz，故FFT/B-Scan算法无法正确估计。

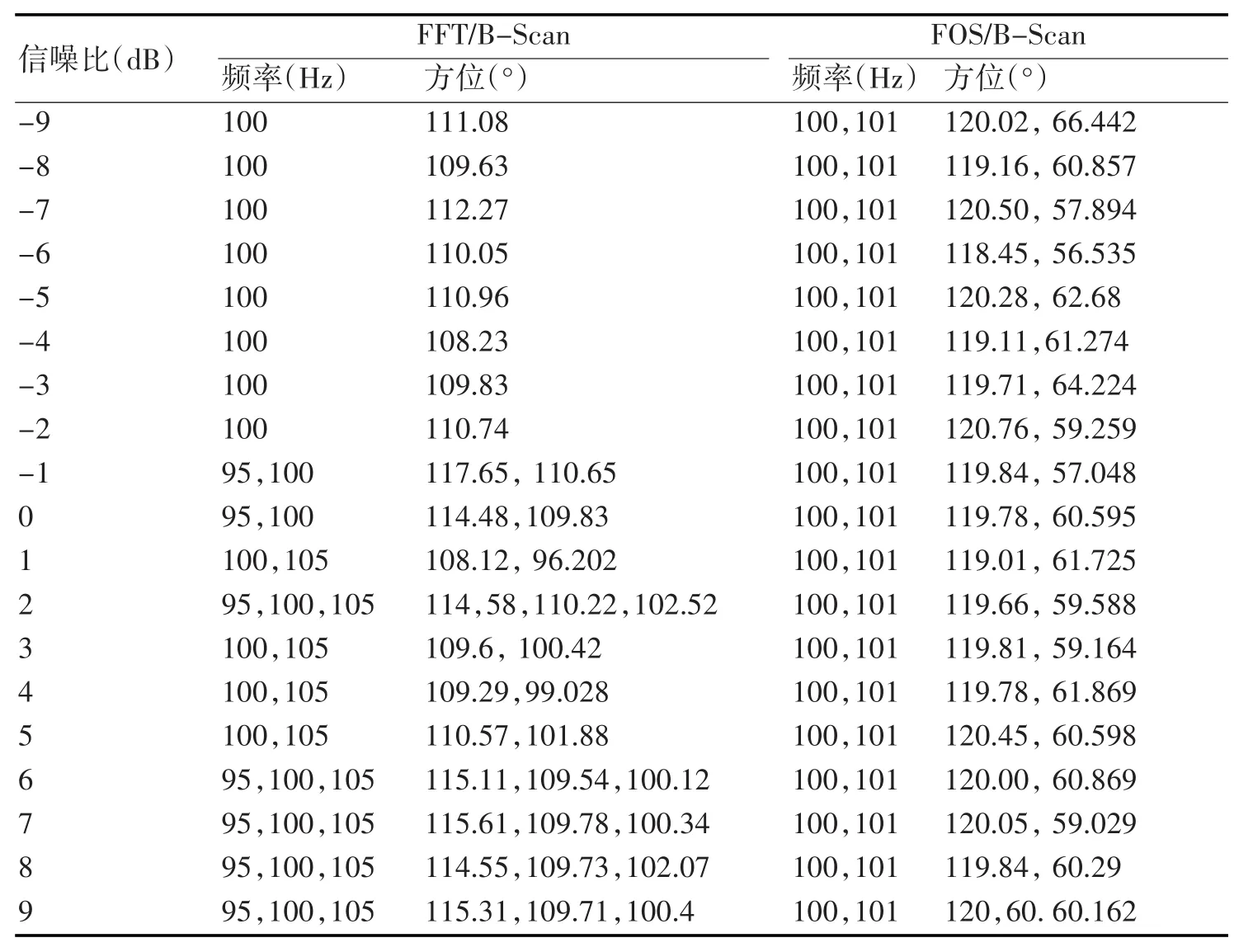
表1 FFT/B-Scan和FOS/B-Scan算法在不同信噪比下的频率和方位角估计

当时间长度增加到T=5s，仿真结果如图4所示。

图4 T=5s时FFT和FOS算法的B-Scan图

从图4中可以看出，尽管数据长度增加，此时FFT算法的分辨率为1Hz，但FFT/B-Scan算法在给定的信噪比下，虽然目标的频率估计准确，但方位仍然无法准确估计，且在错误频点上估计出有目标出现。

当数据长度继续增加到T=10s时，此时FFT算法的分辨率为0.5Hz，仿真结果如下：

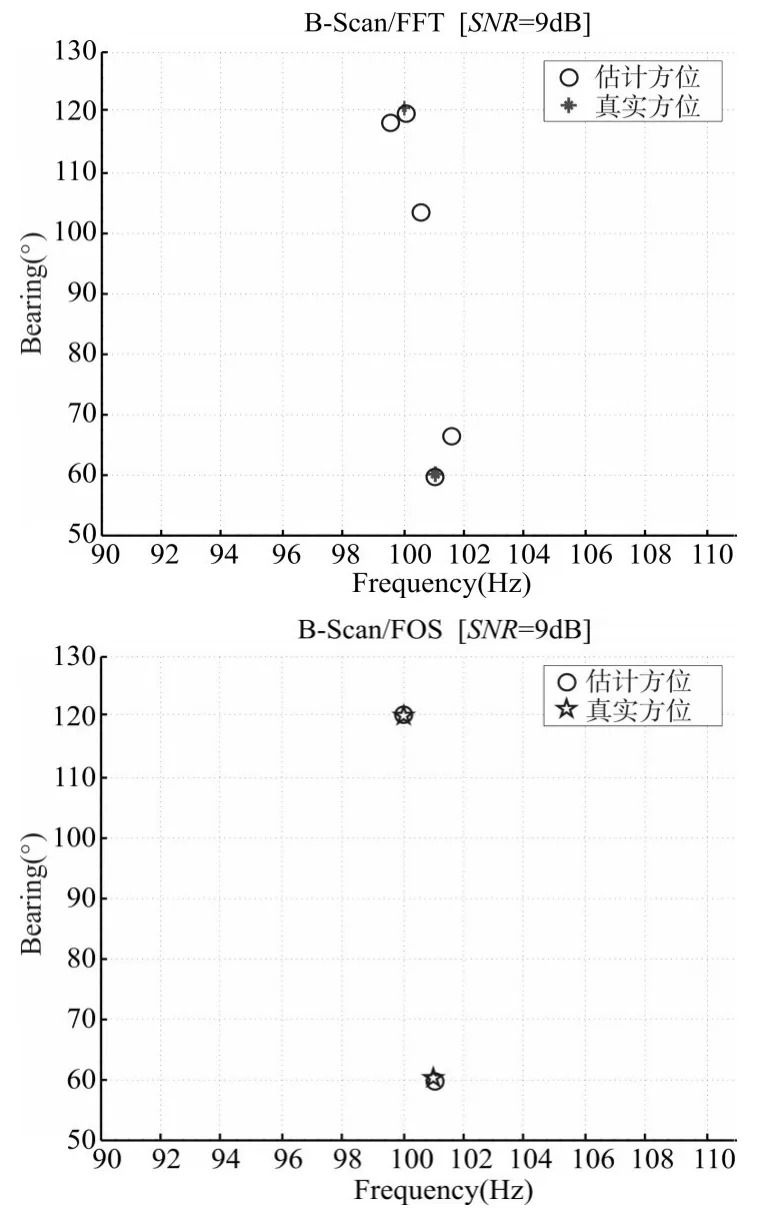
图5 T=10s时FFT和FOS算法的B-Scan图

从图5中可以看出，此时FFT/B-Scan算法准确地估计出目标的频点和方位角，但仍然引入了其他无效信息，给目标探测带来了一定的干扰。

5 结语

通过仿真分析可知，在DIFAR浮标目标方位估计中，FOS较FFT有很大优势，特别是在数据量小和低信噪比情况下FOS的优势能够更加明显地体现出来。在图4中FFT和FOS有相同的频率分辨率，但FFT算法的方位估计效果明显不如FOS算法；在图5中FFT算法的频率分辨率甚至高于FOS算法，虽然FFT算法也估计出了两目标的方位但引入了错误信息，总体效果依然没有FOS算法好，故FOS算法在DIFAR浮标方位估计中性能优于FFT算法。