单纤维和随机多纤维过滤特性模拟研究

2019-02-26陈昌江徐毓亚

纺织科技进展 2019年2期

陈昌江,闫祥,徐毓亚

(1.盐城市纤维检验所,江苏盐城224052;2.盐城三维思滤料有限公司,江苏盐城224500)

0 引言

经济的快速发展也带来了环境的破坏,生态的危机,构建可持续发展,是当今全球共同关注的议题,随着我国GB3095-2012《环境空气质量标准》的实施[1],国家对大气污染物排放要求日趋严格。纤维过滤介质,作为目前应用最广的气体过滤材料,在空气净化中发挥着重要的作用,因此对于单纤维和随机多纤维过滤机理的研究是目前研究的重点。本文基于Open-FOAM软件对单纤维和随机多纤维过滤介质的过滤特性进行数值模拟研究,为纤维过滤介质结构的优化和过滤机理的研究提供参考。

纤维过滤的应用最早可以追溯到古代,当时中国的纺织业领先于全世界,对于过滤理论与机理的研究早在上世纪50年代就已经开始了,早先对纤维过滤介质的研究以实验为主,并且研究对象由简单到复杂。目前,单纤维过滤理论发展最为全面,国外学者Davies[2]在分析了前人的过滤理论研究后,提出了一种新型的单纤维过滤理论,通过将扩散效应、拦截效应以及惯性碰撞效应进行有机结合得出新的纤维过滤实验经验关联式,该理论沿用至今,但是该理论受到小雷诺数的制约。其后,Friedlander[3]发展了单纤维过滤理论,研究在较大雷诺数条件下颗粒物的惯性碰撞,重力效应、纤维拦截以及扩散效应下的颗粒物沉积形态,为单纤维过滤理论发展再添新章。国内对于单纤维过滤理论的研究起步较晚,但近些年通过数值模拟技术有了较多的成果,李水清等[4-5]采取DEM方法模拟了颗粒物在单纤维上沉积过程,模拟出了颗粒物之间的碰撞、颗粒物与纤维之间的黏附效应,取得了较好的结果;付海明等[6-7]通过编程模拟单纤维表面颗粒物的沉积、生长和扩散等过程,分析了多项无量纲参数对颗粒物沉积形态的影响。单纤维的理论研究往往比较单一,而且该理论并不能很好地应用于随机多纤维过滤研究。随着计算机技术的发展,纤维过滤理论更倾向于复杂化、随机化以及应用化发展,因此,随机多纤维理论得到广泛关注。

Hosseini等[8]基于随机算法建立了微观三维模型,基于CFD-DPM模型追踪固体颗粒的运动情况,很好地描述出了颗粒运动轨迹;Sambaer等[9-10]提出了一种利用相应的SEM图像构建三维纤维过滤介质模型的新方法;Wang等[11-13]创新性地使用格子-玻尔兹曼法(Lattice Boltzmann Method)对于二维圆柱纤维模型(平行和交错排列)进行了数值模拟研究;钱付平等[14-15]采用CFD-DEM模型用于模拟平板纤维过滤介质中气-固两相流的双向耦合,很好地模拟出粉尘颗粒在纤维表面的沉积,得到了较为理想的结果;Yue等[16]也建立了三维随机结构的纤维过滤器,利用CFD-DEM模拟平板型过滤介质内部流场并计算过滤介质的过滤效率和压降。

基于纤维过滤介质微观形态,分别建立了单纤维和随机多纤维过滤介质的微观3D模型,利用Open-FOAM软件对两种模型内部气-固两相流进行数值模拟。通过网格依赖性和试验结果验证模拟结果准确性,分析在不同粒径和不同单位沉积量条件下纤维过滤介质的过滤效率,得出相关纤维过滤介质的过滤机理,为深入研究单纤维过滤发展随机多纤维过滤机理提供一定的理论依据。

1 数值模型建立

1.1 单纤维模型

如图1所示,通过对比实际纤维过滤介质的微观扫描电镜图片(图1(a))可知,某单根纤维形态与膨胀的直线(圆柱体)十分相似,因此将单纤维数值计算模型近似地简化为圆柱体(图1(b))。随后将建立好的stl格式模型导入Open FOAM,运用Open FOAM里面子库网格划分工具blockmesh对其进行六面体网格划分,得到单根纤维网格划分后的文件(图1(c))。

1.2 随机多纤维模型

目前的计算机水平,建立纤维过滤介质的单纤维模型十分简单,但要建立出与真实纤维十分一致的随机多纤维3D模型相对较难。如图2所示,通过获取纤维过滤介质切片,确定纤维端面的准确位置和中心线的位置,通过端面位置固定在两端的中心获取随机变换曲率的曲线簇,根据曲线簇通过MATLAB软件变成生成随机多纤维过滤介质微观3D模型(图2(b)),并将模型通过ANSYS-ICEM软件对其进行混合网格的划分,并对纤维区域进行加密处理(图2(c))。

图1 单纤维模型建立及网格划分

图2 计算边界设定

纤维过滤介质的数值计算模型是由简到繁的过程,模拟初期对纤维过滤介质的建模绝大多数是二维或者单纤维的模型,其后纤维过滤介质的三维建模技术有很大的提升,近些年,纤维过滤介质的微观3D建模技术得到较好的发展。除了模型的越来越贴近与真实纤维过滤介质微观形态,随着CFD模拟技术的发展,对于纤维过滤介质也从单相发展到多相。

2 数值模拟验证

2.1 模拟边界设置

在进行OpenFOAM中MPPICFoam求解器计算时,为了能够让气流场稳定后注入颗粒,气流从入口(Inlet)注入,固体颗粒物从内部面注入,颗粒和气体从同一出口(Outlet)逃逸。计算区域四周的边界均设为对称边界条件(Symmetry),纤维表面边界设置为无滑移固壁边界条件。图3为单纤维和多纤维过滤介质边界条件设置。

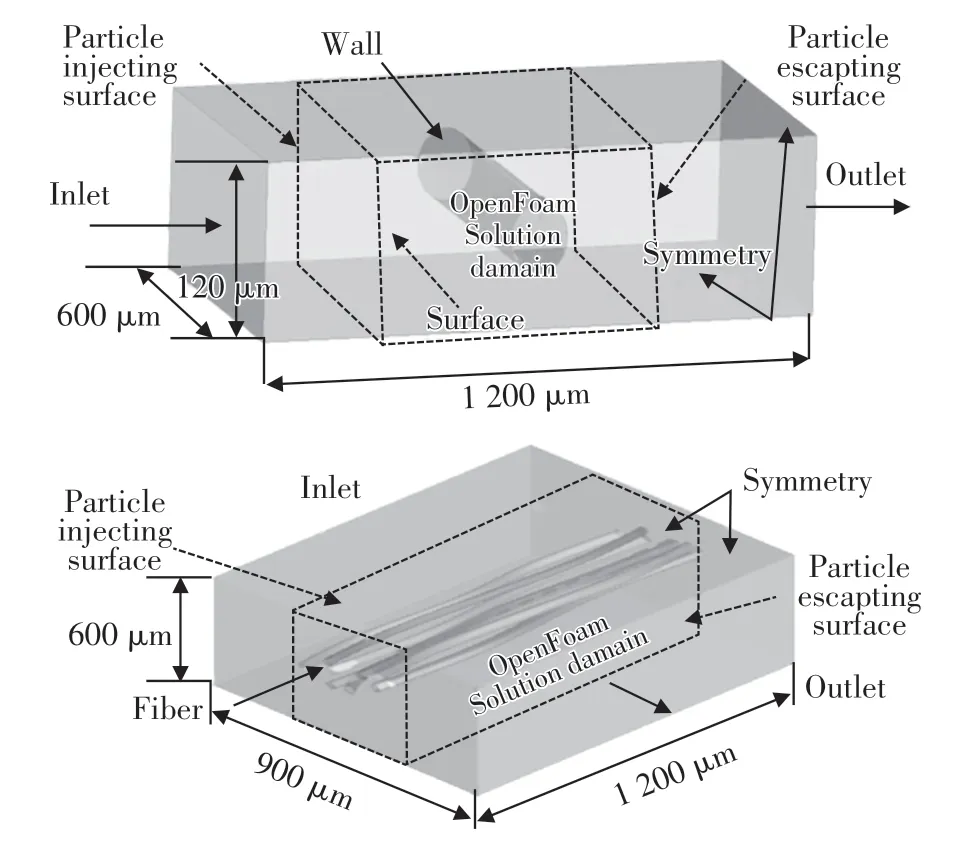
图3 计算边界设定

2.2 网格依赖性验证

建立纤维过滤介质微观过滤性能的数值模型是比较精细的过程,网格的数量直接影响到模拟计算速率与精确度,分别对单纤维六面体网格以及随机多纤维四面体六面体混合网格进行了网格依赖性验证。通过分析压降的变化趋势来判断网格数量对于纤维过滤介质模拟结果的影响(图4)。

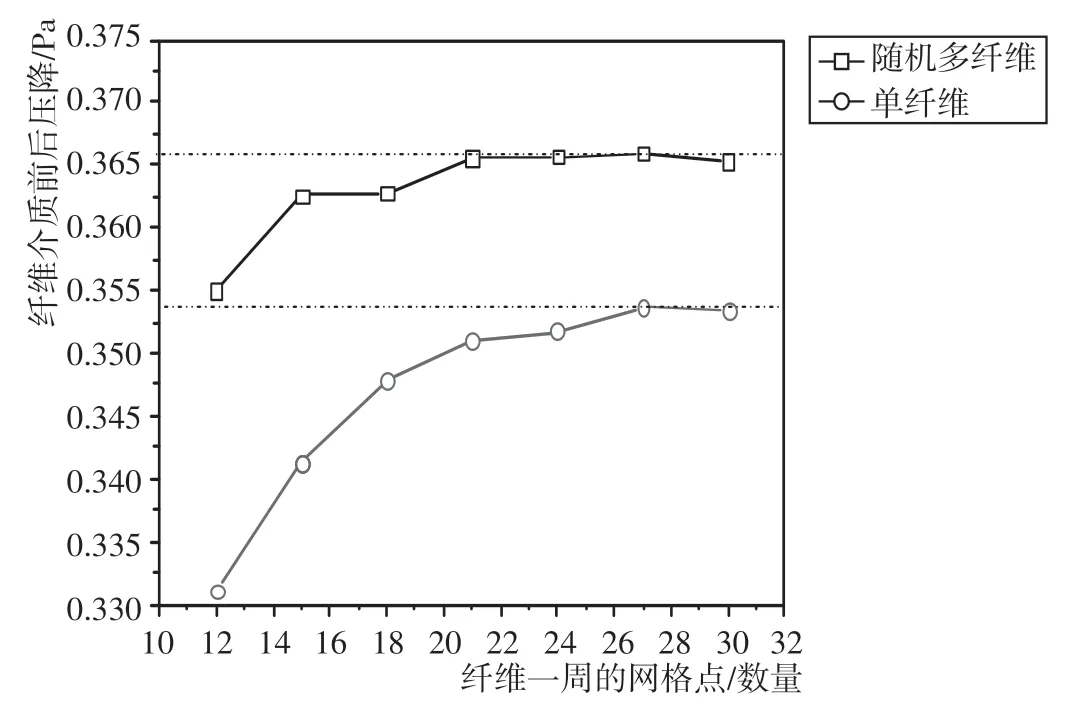
图4 网格数量对压力损失的影响

通过对比单根纤维周围不同网格点的数量对纤维过滤介质前后过滤压降的影响,由图4中可以看出,单纤维和随机多纤维网格中,单根纤维一周的网格点数为20以后均达到较为稳定的状态,综合模拟计算速率与模拟精确性,选择20点为网格数量用于数值模拟,单纤维过滤介质网格数量保持在5万左右,随机多纤维网格数量大致为100万。

2.3 过滤实验验证

由图5可以看出,选取单纤维和随机多纤维模拟结果与试验结果进行对比,用于判断模拟结果的精确性,从图形的变化趋势中可以看出,入口速度对纤维过滤介质过滤压降具有很大的影响,随着入口风速增大,纤维过滤介质压降越大,且呈线性增加。对比Open-FOAM模拟结果与Davies实验关联式[2]发现两者变化趋势基本保持一致,因此判断Open FOAM对于纤维过滤介质内部气-固两相流数值模拟结果可信,为纤维过滤介质过滤特性的研究分析提供了依据。

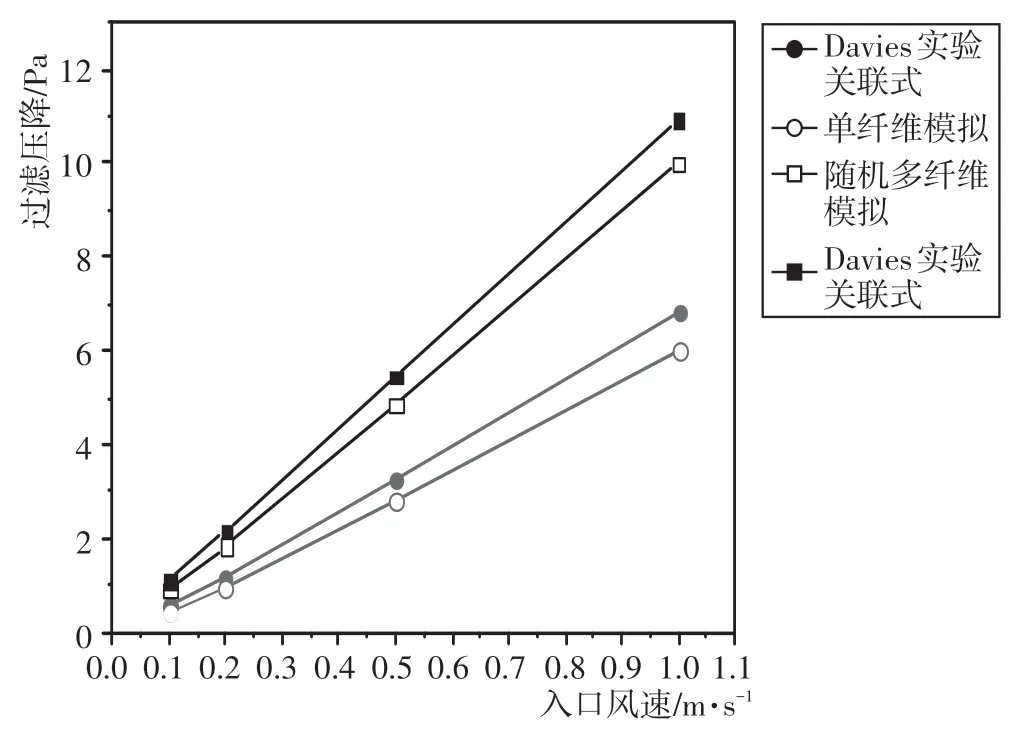
图5 压降与入口风速的关系

3 结果与分析

3.1 模拟结果

图6展示了单纤维内气-固两相的数值模拟结果,可以看出固体颗粒物从入口随气流进入流场,由于纤维过滤介质的拦截、扩散和碰撞效应,颗粒物接触到纤维过滤介质后被纤维过滤介质捕集,沉积在纤维过滤介质表面。一部分颗粒物从边缘的缝隙中逃逸,图6中可以看出单纤维的存在能够很好地捕集固体颗粒物,过滤初期颗粒物比较均匀地分布在单纤维的表面,主要是纤维对颗粒的捕集起主导作用。

图7展示了随机多纤维内气-固两相的数值模拟结果,可以看出固体颗粒物从入口随气流进入流场,随机多纤维由于多层次的纤维分布,颗粒物通过多重拦截、碰撞效应,被纤维过滤介质捕集,沉积在纤维过滤介质表面。

3.2 过滤特性分析

图8显示了单纤维和随机多纤维对颗粒的分级效率与Kuwabrara经验模型[17]的比较。从图8中可以看出,无论是单纤维还是随机多纤维过滤效率都随着颗粒粒径的增大而增大。颗粒粒径增大时,其惯性碰撞和拦截作用增大,而扩散效应是逐渐降低的,扩散效应是对于粒径小于1μm以下的,3μm以上的粒径的颗粒这里可以忽略不计。因此纤维过滤介质的总分级效率增大。这正验证了文献[17]中的结论。

图6 单纤维气-固两相流数值模拟

图7 随机多纤维气-固两相流数值模拟

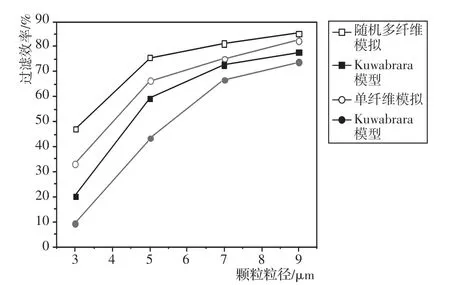
图8 不同固体颗粒物粒径纤维滤料被捕集数量

与Kuwabrara经验关联式相比,本文模拟的效率值稍微偏大,但是总体趋势是一致的。偏大主要是由于模拟设置纤维壁面属性是颗粒与纤维壁面碰撞接触直接被捕集,因此会稍大于经验模型。随着固体颗粒物直径的增加,过滤效率增长速率会逐渐降低,而且在固体颗粒物粒径开始增加阶段,捕集效率增加得很快,之后会迅速降低。由此可见,影响颗粒物捕集效率的因素还有其他原因,如沉积在纤维表面的固体颗粒物对固体颗粒物的捕集作用,致使颗粒物沉积的主导因素有纤维捕集转为颗粒捕集的过程。

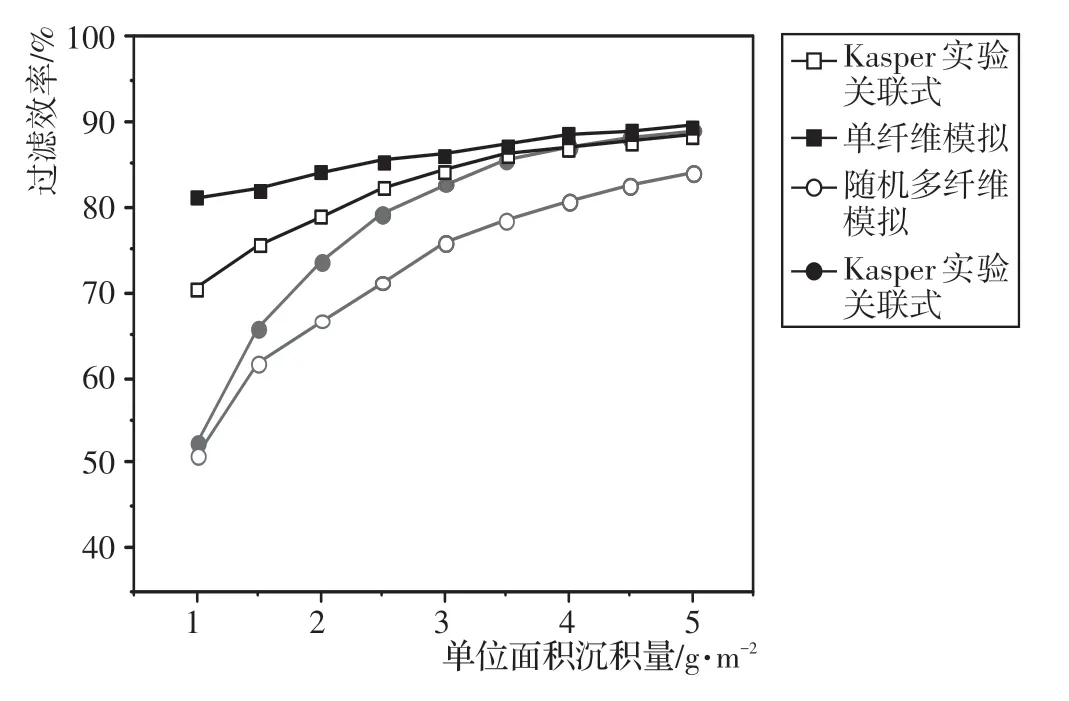
图9 过滤效率随单位沉积量的变化趋势

研究颗粒物对于颗粒物的捕集是分析非稳态纤维过滤机理的重要阶段。图9展示了纤维过滤介质过滤效率随着单位面积沉积量的变化趋势,并将模拟结果与Kasper[18]试验结果进行对比。随着固体颗粒物沉积质量的增加,过滤效率会逐渐上升,但是单纤维增长的速率较快,幅度较大,这是因为单纤维表面的颗粒沉积快,很容易形成堆积状态,而随机多纤维因为存在层次性,使得纤维表面形成的颗粒堆积不明显。整体趋势表现在固体颗粒物粒径开始沉积,捕集效率低,但是提升潜力大,之后会迅速增加;沉积阶段颗粒物的捕集效率高,但是提升潜力小,整体过滤效率增长不明显。