基于无网格界面模拟方法的面板坝防渗体跨尺度分析
2019-02-26邹德高孔宪京刘京茂屈永倩
邹德高,龚 瑾,孔宪京,刘京茂,屈永倩
(1.大连理工大学 海岸和近海工程国家重点试验室,辽宁 大连 116024;2.大连理工大学 水利工程学院,辽宁 大连 116024)
1 研究背景
面板堆石坝在近些年得到迅猛的发展[1],我国也正处在从200 m级到300 m级面板堆石坝的关键研发阶段。随着工程规模的逐步增加,给以有限元为主的数值模拟方法带来巨大挑战[2]。混凝土面板作为大坝关键的防渗结构,其安全性态至关重要。因此混凝土面板需采用较密的网格模拟其应力分布[3],然而面板与堆石体尺寸相差悬殊,若在堆石体区采用一致尺寸的网格,无疑大大的增加了不必要的计算成本,因此跨尺度建模对面板坝精细化分析有着重要意义。
在面板坝跨尺度模型中,传统的点对点界面单元(Goodman单元,薄层单元)[4-5]无法连接不同尺寸的面板网格与垫层区网格。针对上述问题,学者们做出相应的研究。周墨臻等[6-7]通过接触力学算法代替界面单元实现荷载的在疏密网格间的传递,但该方法较难描述界面处在地震荷载下复杂的变形[8]。钟红等[9]采取逐渐过渡的方法实现跨尺度建模,但是这种方法需要大量的人工干预且不适合三维模型。Chen 等[10-12]结合比例边界有限元和四分树技术实现了在堆石体区域的疏密网格的自动拋分。Qu等[13-14]开发的非对称界面单元实现了两侧不同尺寸网格的连接,但该界面单元部分节点仍需对应且不适合局部网格优化等问题。
若能实现界面两侧节点自由分布,摆脱点对点限制,则可弥补上述方法的不足,解决面板坝中跨尺度的难题。而与有限元相比,只需要节点信息的无网格法更能满足要求。最早出现的无网格法是由Lucy提出的SPH法[15],应用于天体问题。1994年Belystschko等[16]提出了基于背景网格的EFG法,随后无网格法快速发展,并在裂纹扩展、流固耦合和液化大变形等方面[17-20]得到了广泛的应用。
本文将无网格法[21-22]拓展到土与结构界面的模拟中,以实现界面两侧节点自由分布且无需对应,该方法可直接连接尺寸不同的网格,从而简化了跨尺度建模及局部网格优化的过程。同时基于该方法对一200 m级面板堆石坝进行跨尺度分析,并与传统Goodman单元对比,证明该方法在面板坝静力分析和动力分析中具备足够的精度。同时建立防渗面板与垫层区跨尺度分析模型,通过对比计算结果及计算时间,证明无网格界面在保证面板模拟精度的前提下,可大幅度减少堆石体的网格,从而提高计算效率。该方法很容易扩展到三维并为面板坝面板精细化损伤演化分析提供有效的技术手段。
2 基于无网格的非点对点界面模拟方法
2.1 理论概要及相关公式推导基于无网格的非点对点界面,两侧节点自由分布且无需对应。高斯点的生成和积分过程均在引入的背景网格线上进行。图1、图2为一个典型无网格界面及高斯点分布。根据相对距离,确定高斯点支持域内节点,并通过径向插值函数(RPIM)[22]计算相应插值点位移。图3所示为一高斯点分别在界面两侧支持域内的节点。插值点在界面上、下两侧位移可表达为(这里仅以上侧位移为例):
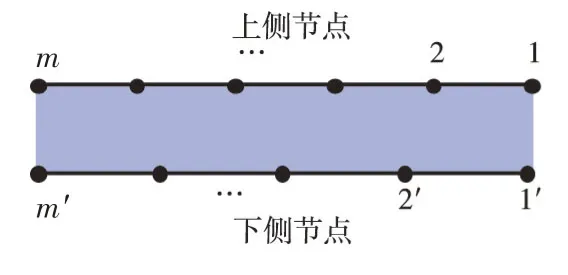
图1 基于无网格的非点对点界面
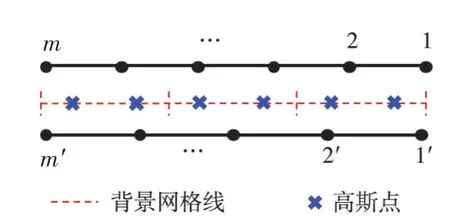
图2 背景网格线及高斯点分布
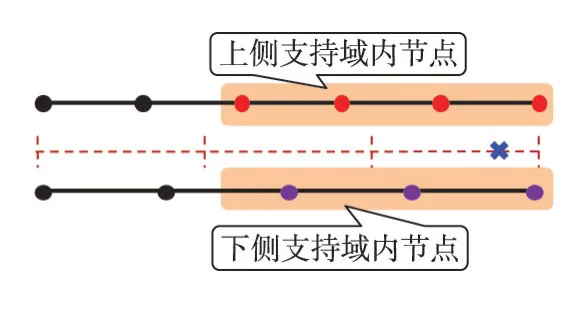
图3 高斯点支持域内节点
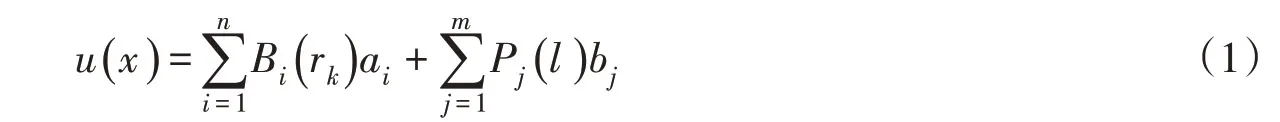
式中:ai、bj为待求常数;l为各节点局部坐标;rk为各节点与高斯点距离;Bi(rk)为径向基函数(RBF),常见的径向基函数有许多种,本文采用MQ基函数,MQ基函数中包含c、q两个形状参数,根据Liu等[23]的数值试验,本文中c=3,q=1.03;Pj(l)为在径向基函数中增加的线性多项式,增加的线性多项式为[1l];n为径向基函数个数,即表示高斯点支持域内节点数量;m为多项式基函数个数,本文中m=2。

式中:dav为支持域内节点平均间距。
联立式(1)和式(2)可得到如下矩阵方程:

上式中各矩阵表达式为:
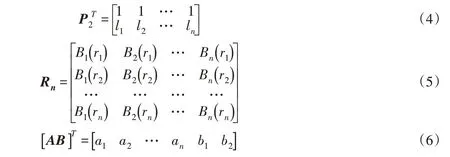
将式(4)—式(6)带入式(3)中,求解可得:
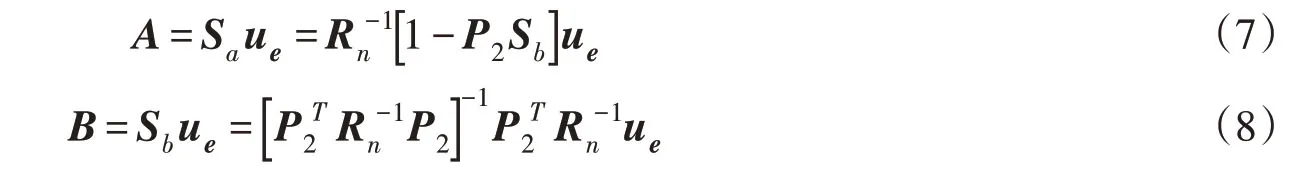
将式(7)和式(8)带入式(1),则插值点在界面上侧位移可表示为:
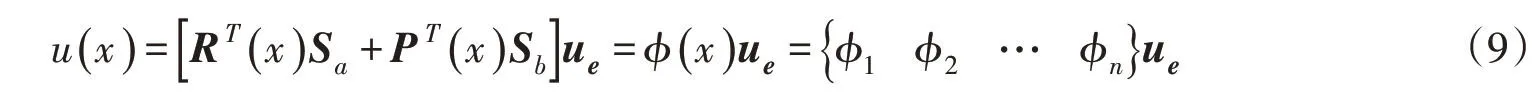
式中:φi为插值点在界面上侧支持域内各节点处形函数;ue为各节点处位移插值点处相对位移,可表示为:

由此可得到应变转化矩阵Bi:
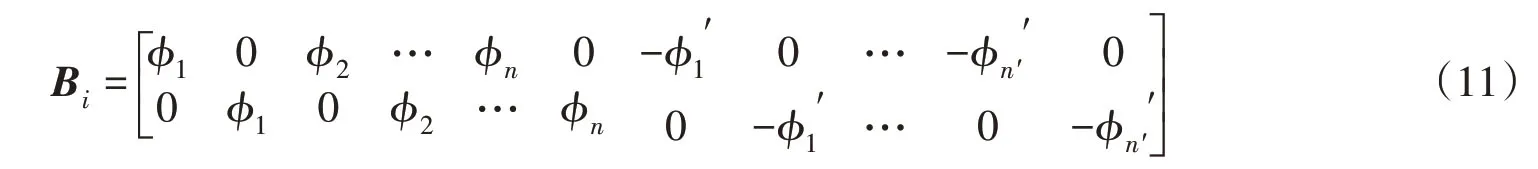
式中:φi、φi'分别代表插值点在界面上、下两侧支持域内各节点处形函数;n、n′分别代表插值点在界面两侧支持域内节点个数。
求得应变矩阵后,引入界面本构[24]矩阵Di,并在背景网格线内进行高斯积分得到刚度矩阵:

以上公式均在局部坐标下求得,通过坐标转化矩阵可将上述刚度阵、内外力矩阵转化到整体坐标系下。最后根据节点编号,将上述矩阵组装整体刚度阵及不平衡力中,由平衡方程求解各节点处位移:

从上述的推导中可以看出,无网格界面与Goodman 界面单元主要的区别在于高斯点位移的插值模式分别为径向插值函数和线性插值及界面两侧节点分布上,两种方法均可通过界面本构矩阵来反映土体与结构之间的切向、法向接触关系。
2.2 改进RPIM插值函数径向插值函数(RPIM)在求解域内部具有很高精度,然而在边界附近由于一侧支持域内节点减少,RPIM插值精度有所降低。通过引入虚设节点,结合有限元线性插值的优势可改进RPIM插值函数,图4所示为该方法的主要流程。
(1)首先在求解域内边界增设虚节点。
(2)通过RPIM计算虚节点处位移,具体过程参考式(1)—式(10),虚节点处位移可表示为:
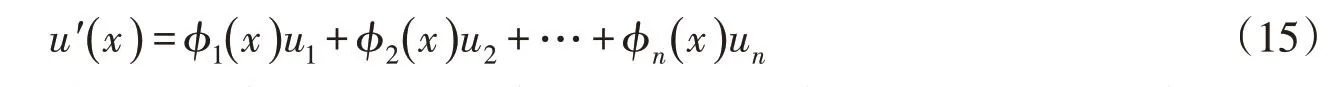
(3)判断插值点位置,如果插值点位于求解域内部,依然通过RPIM求该点位移,若插值点位于边界附近,则通过虚节点和边界处节点线性插值计算:

将式(15)带入式(16),最终插值点位移可由各节点处位移表示:
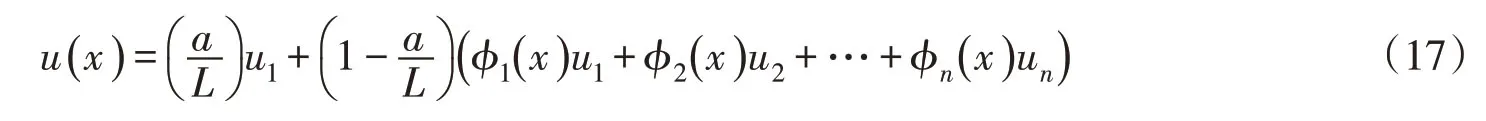
由改进的RPIM插值函数计算得到节点3处的形函数如图5所示。修正后的RPIM继承原插值函数基本性质,即:(1)δ函数性质;(2)单位分解性;(3)再生性;(4)紧致性;(5)连续性。
通过曲线拟合测试验证改进RPIM插值函数精度。本文选择函数y=sinπx,在[-2,2]区间设置11个均匀的计算点并求其函数值,通过与理论值对比,图6绘制了两种插值函数误差曲线。表1总结了在(-2,-1.9]区间两者误差对比。
改进的RPIM 插值函数结合RPIM和有限元线性插值的优点,在保证原插值函数优势的前提下,进一步改善了边界附近的插值的精度,并将改进的RPIM插值函数引入非点对点界面中。文中无网格界面插值函数均采用改进的RPIM计算。

图4 改进的RPIM插值函数实现过程
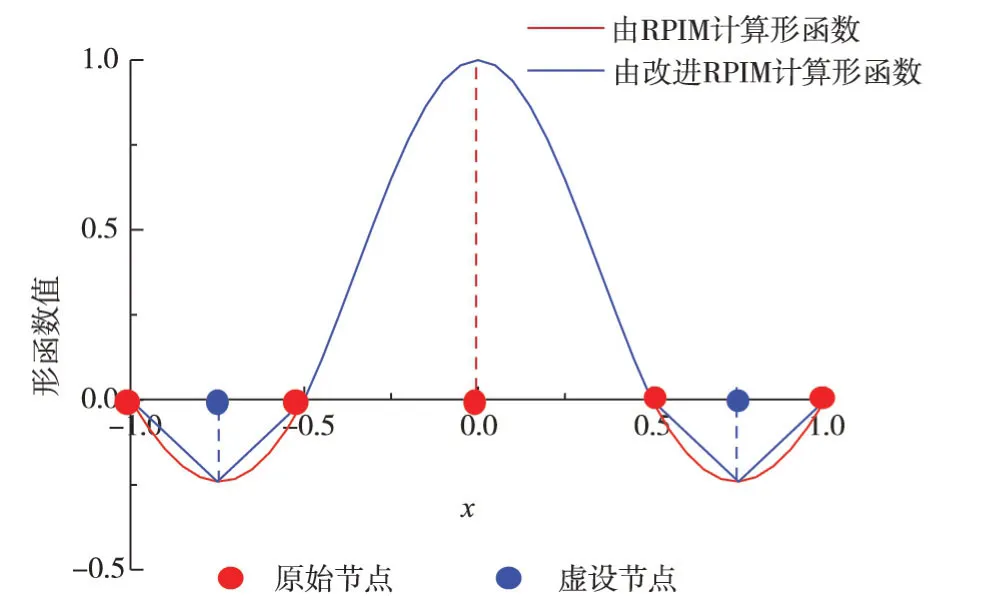
图5 形函数对比
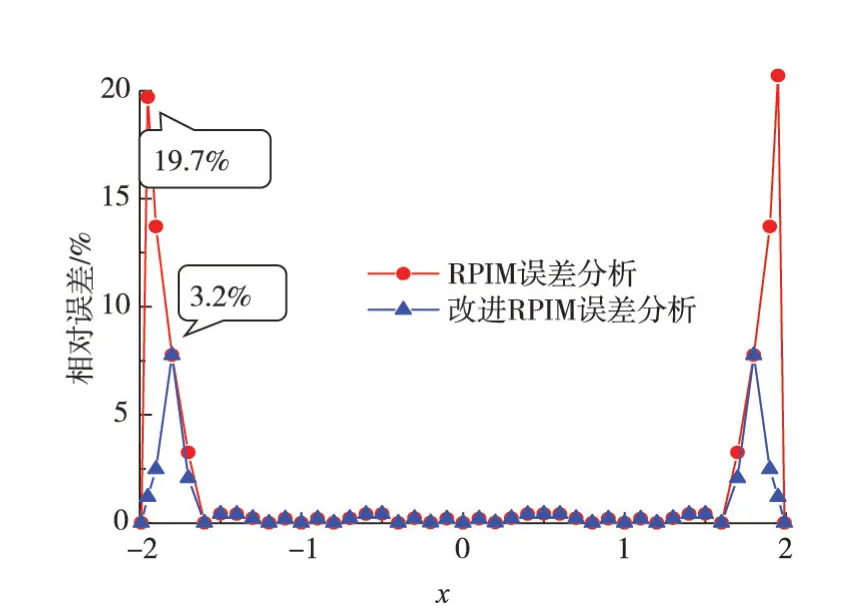
图6 误差分析对比

表1 两种插值方法在(-2,-1.9]误差对比
2.3 数值程序实现本文基于课题组自主开发的GEODYNA 软件平台,采用面向对象程序设计思想及C++语言,将基于无网格的界面模拟方法封装成一个超单元并整合到GEODYNA中,实现与FEM无缝耦合,并可应用复杂弹塑性界面本构。非点对点界面程序框架如图7所示。首先抽象出其与有限元的共同特征(计算形函数,求解刚度阵、质量阵、阻尼阵等),进而设置相应的成员函数及内部继承关系,其次根据非点对点界面自身的性质,设置外部调用接口及特有的成员函数。最终将基于无网格的非点对点界面在限元框架下实现。
3 面板堆石坝中的应用
3.1 算例模型某面板堆石坝,坝高200 m,上游坡比1∶1.5,下游坡比1∶1.6,坝顶宽度18 m,面板顶部宽度0.3 m,坝体部分为主堆石区及垫层区。为保证面板在静、动力作用下的模拟精度,面板沿厚度方向分为5层单元,沿坝坡方向长度2 m。面板与垫层界面分别用有厚度Goodman单元及基于无网格的非点对点界面来进行模拟,两种方法均不同于传统无厚度Goodman单元[4],法向刚度不再是个很大的常数[25],其法向刚度可与周围土体刚度大小相兼容,可较好地模拟接触带的法向剪缩、剪胀变形(或法向刚度)特性。算例局部网格如图8所示。
3.2 材料参数在静、动力计算中,堆石料及垫层材料均采用堆石料广义塑性模型[26-27],材料参数分别列于表2、表3,表2、表3中G0、K0、ms、mv为与弹性模量相关系数,Mg、Mf、af、ag为与塑性流动方向相关系数,其余为与塑性模量相关系数。面板与垫层间的界面采用界面广义塑性模型[28],参数见表4,表4中Ds0、Dn0为与弹性模量相关系数,km、Mf、α、rd为与塑性流动方向相关系数,a、b、c为与颗粒破相关系数,Mc、er0、λ为与临界状态相关系数,k、H0、fh为与塑性模量相关系数。在界面广义塑性本构模型中可直接引入厚度t来考虑接触带沿厚度方向的特性。面板、趾板及基岩部分采用线弹性模型,参数见表5。静力计算时,坝体经40个荷载步完成填筑,并分38个荷载步蓄水至190 m高程。
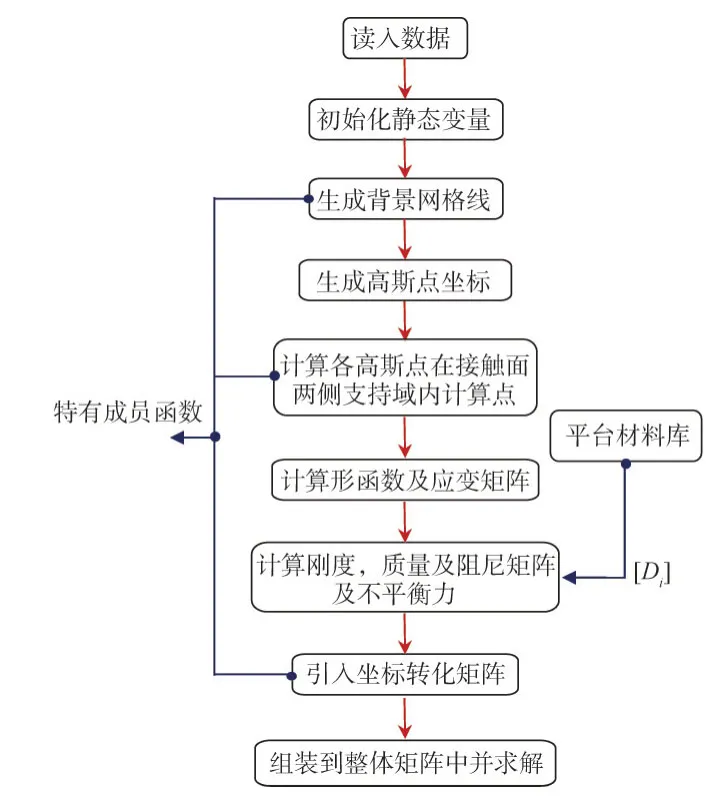
图7 基于无网格的非点对点界面程序框架
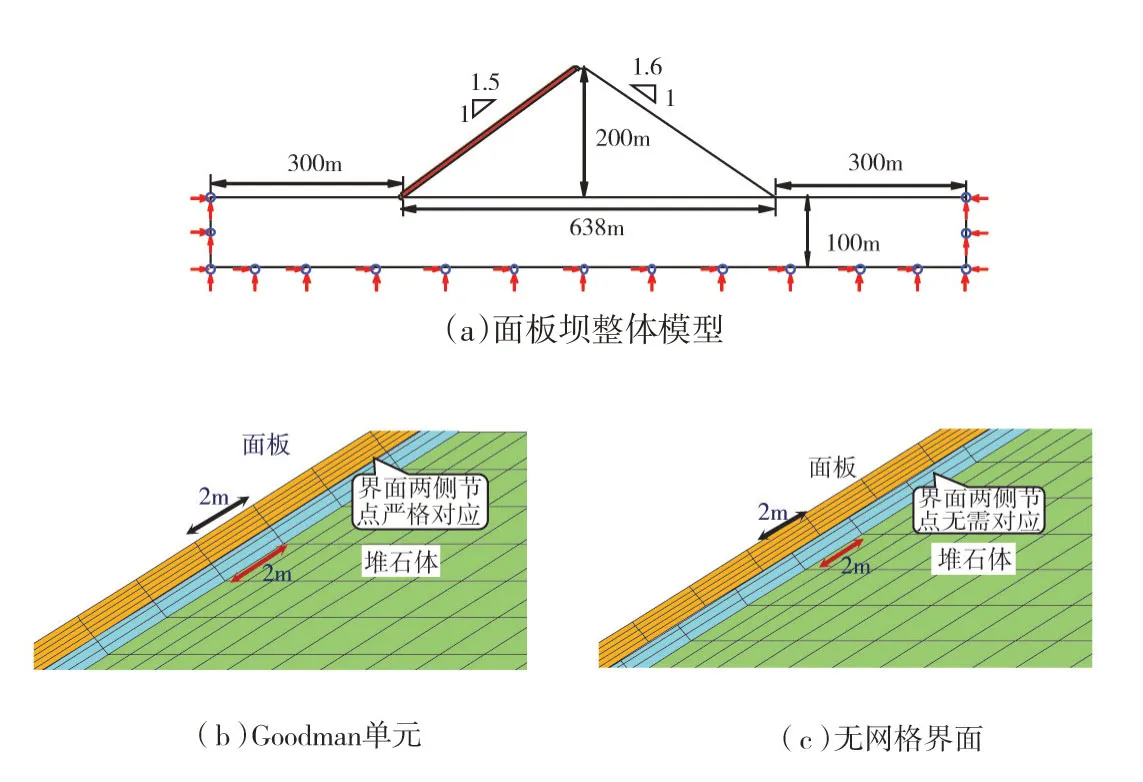
图8 CFRD网格对比
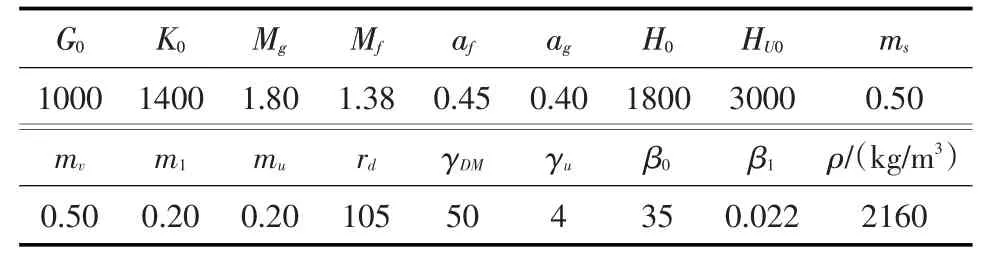
表2 堆石料广义塑性模型参数

表3 垫层料广义塑性模型参数
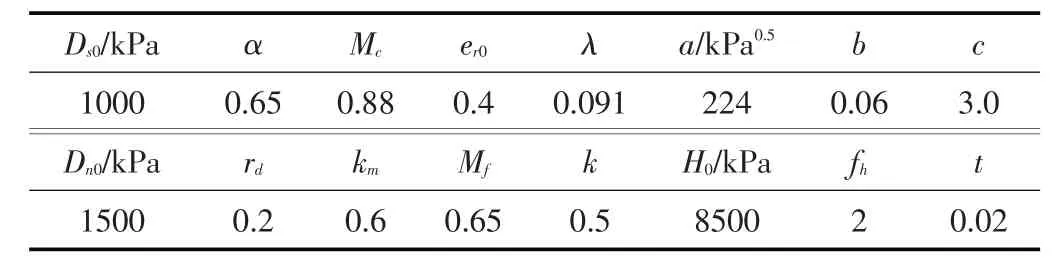
表4 界面广义塑性模型参数
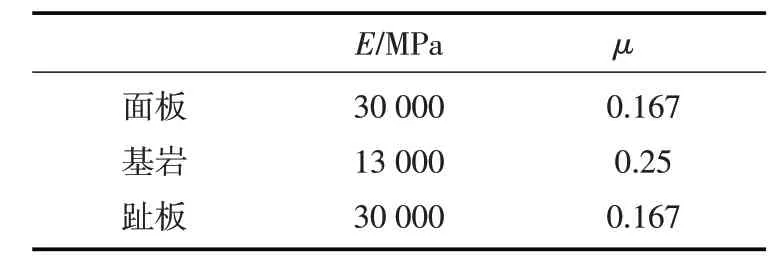
表5 线弹性材料参数
3.3 地震动输入根据现行的《水工建筑物抗震设计规范》规定的标准反应谱,生成水平向及竖向人工模拟地震波。顺河向地震动峰值为0.3g,竖向地震动峰值为0.2g,地震波持时25 s。地震波加速度时程如图9所示,地震采用波动法输入,计算步长Δt=0.01s。
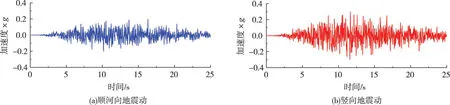
图9 地震动加速度时程
3.4 计算结果分析首先给出静力计算结果,两种模型在满蓄期主应力及面板顺坡向应力的对比。图10为堆石坝满蓄期坝体最大、最小主应力。图11为满蓄期面板(面板中间层单元)顺坡向应力(压为负)对比。
无网格界面实现了两侧节点自由分布且无需对应。图10表明,无网格界面与Goodman单元两种计算方法相差较小。证明了无网格界面在面板堆石坝静力分析中具备足够精度。
同时将无网格界面应用于面板坝动力分析中。图12为在地震荷载作用下下面板最大、最小顺坡向应力(压为负),图13为面板顶部加速度时程曲线。
由图12、图13可以看出,两种算法在地震中面板应力相差较小,面板顶部加速度时程一致,证明了基于无网格的非点对点界面在面板坝动力分析的可行性。

图10 满蓄期坝体应力(单位:MPa)
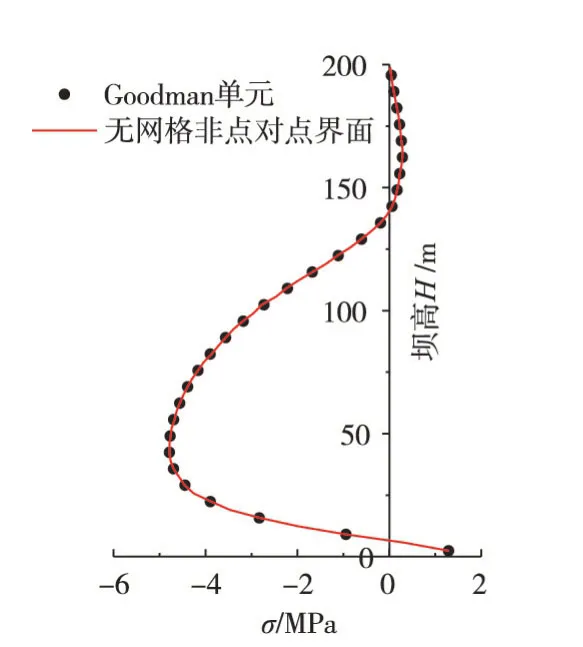
图11 满蓄期面板顺坡向应力
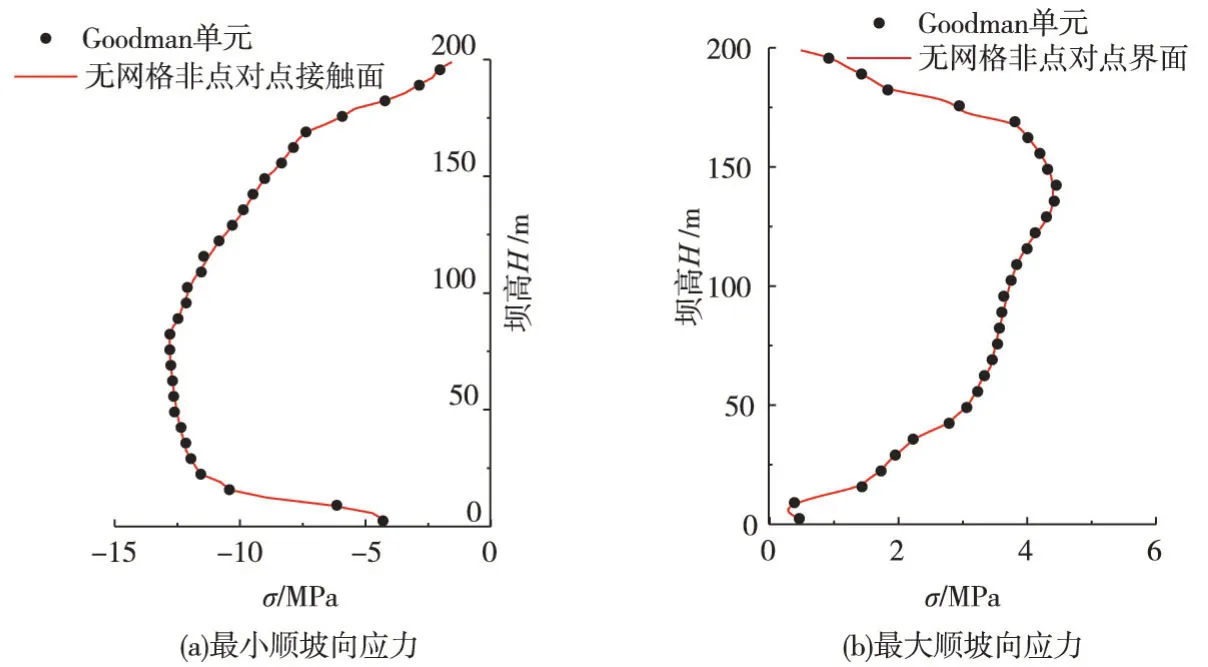
图12 地震作用下面板顺坡向应力
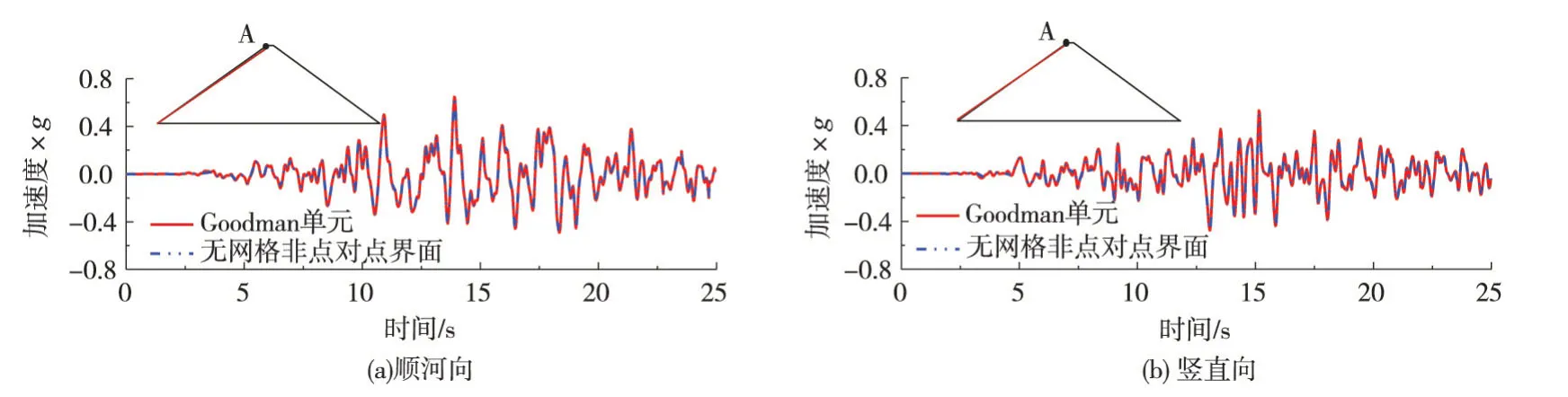
图13 面板顶部A点加速度时程曲线
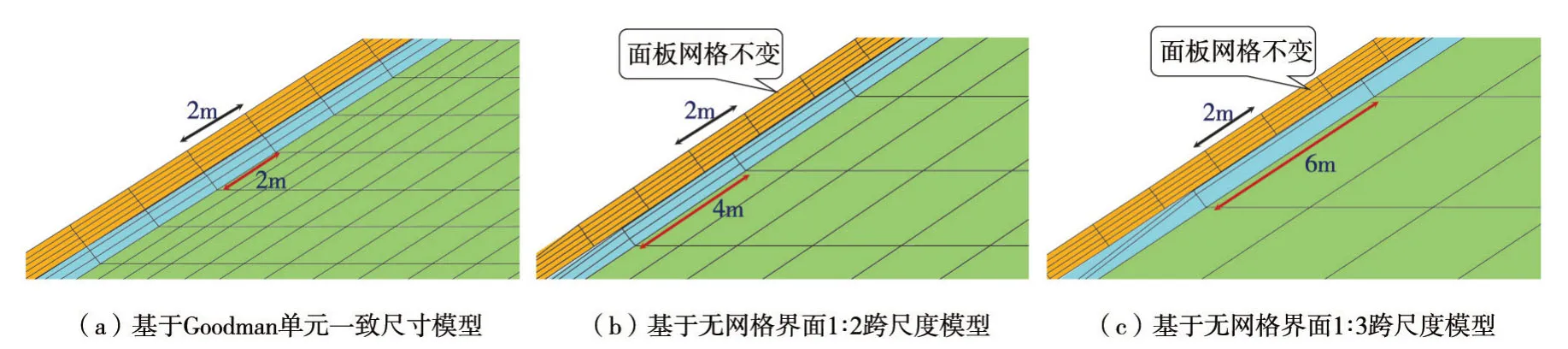
图14 不同比例的面板和垫层跨尺度模型
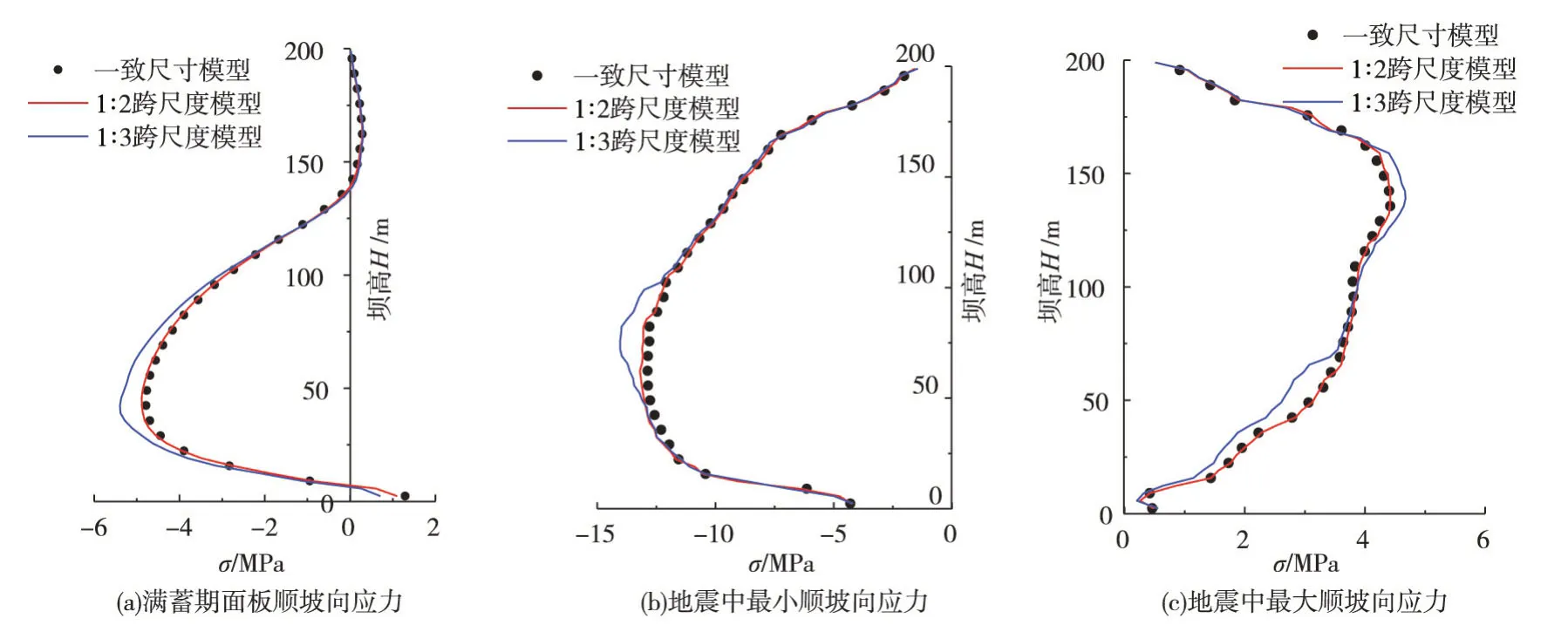
图15 面板顺坡向应力
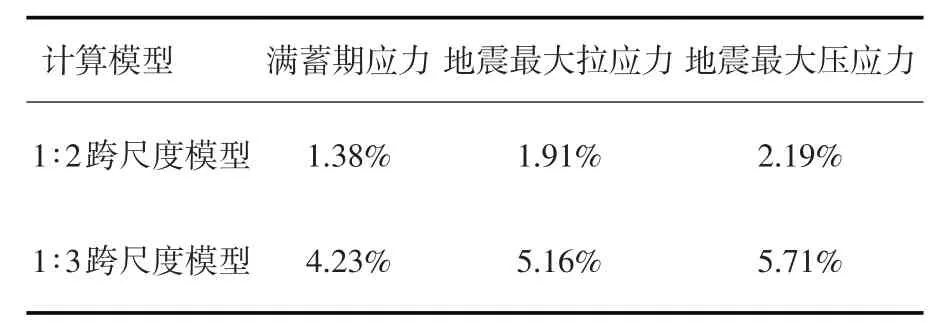
表6 平均相对偏差
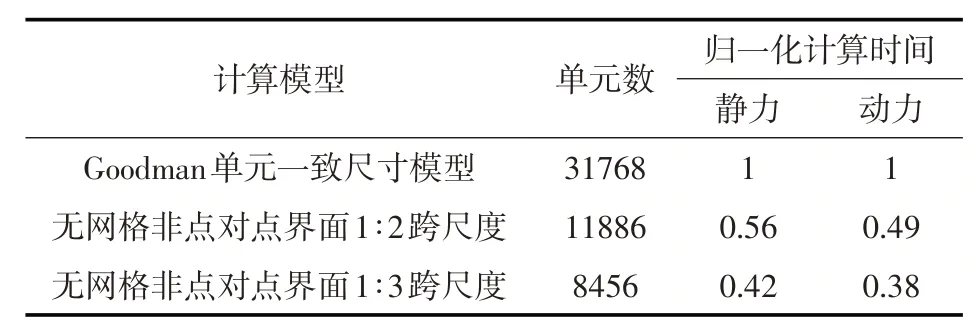
表7 计算效率对比
3.5 高效跨尺度建模及分析面板采用精细化网格模拟后,由于在堆石体区采用一致尺寸的网格,总单元数达31 768 个,无疑增加了不必要的计算成本。非点对点界两侧节点自由分布且无需对应,因此可连接不同尺寸的面板与垫层区网格,进而实现面板坝的跨尺度分析。在图8(c)基础上保持面板网格不变,将堆石体用相对较疏的网格替换,通过替换不同尺寸的网格,实现不同比例的跨尺度建模。图14为通过非点对点界面实现的面板和垫层顺坡向尺度跨越(分别为1∶2和1∶3)。
采用上述的材料及地震输入,分别对不同比例的跨尺度模型进行静动力分析。图15为各模型面板顺坡向应力比较(压为负)。表6给出不同比例跨尺度模型与有限元一致尺寸模型计算结果的平均偏差,表7给出了各模型的单元总数及静、动力计算时间。
结果表明,无网格界面很容易实现了面板坝跨尺度分析,并可大幅提高计算效率。在跨尺度比例为1∶2时,结果与有限元一致尺寸网格基本一致,而1∶3时差计算结果产生一定偏差但控制5%左右。因此,在应用非点对点界面对面板坝进行分析时,面板与垫层区网格顺坡向尺寸跨越可控制在1∶2到1∶3 之间,在保证精度的前提下,显著提高计算效率。如果继续考虑在堆石区内进行疏密网格过渡,可进一步提高计算效率[10-12]。
4 结论
通过引入背景网格线及径向插值函数(RPIM),开发了基于无网格的界面模拟方法,实现了界面两侧节点自由分布且无需对应,并可灵活地连接不同尺寸面板与堆石体网格,进而建立了面板与垫层跨尺度分析模型。(1)基于无网格的非点对点界面,可通过自由分布且无需对应的节点连接不同尺度的面板与垫层区网格,从而实现对面板坝跨尺度分析。(2)通过更新无网格界面两侧的节点,替换后的堆石体网格可直接与面板原始网格相连,简化了局部网格精细化的过程。(3)通过改进的径向插值函数(RPIM)计算得到无网格界面的形函数,在保持无网格界面优势基础上,提高了边界附近的插值精度。(4)计算结果表明,采用无网格界面对面板坝进行分析时,面板与垫层区网格顺坡向尺度跨越可控制在1∶2到1∶3之间。在保证计算精度的前提下,大幅度提高计算效率。
该方法很容易拓展到三维界面的模拟中,效率提高程度将比二维更加明显,可以为面板坝面板损伤演化精细化分析提供有效的技术手段。
