高土石坝-地基动力相互作用的影响研究

孔宪京，周晨光，邹德高，余 翔

（1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；2.大连理工大学 建设工程学部水利工程学院，辽宁 大连 116024；3.郑州大学 水利科学与工程学院，河南 郑州 450001）

1 研究背景

随着水电能源需求的持续增长，由于土石坝具有可就地取材、地质地形适应性强以及便于大规模施工等优点，近二十年来得到了高速发展，坝高已达到300 m级[1-3]。因此，保障高坝大库长期安全运行是关乎国计民生的大事，尤其是地震条件下的安全性备受关注，准确分析大坝的地震反应对其安全评价及抗震设计至关重要[4-5]。

在大坝地震反应分析时，就地震动输入而言，运动方程的求解有两类方法[6]，即作为封闭系统的振动问题（振动分析方法）和作为开放系统的波动问题（波动分析方法）。刚性地基条件下作为振动问题求解时，不考虑结构与地基的动力相互作用，如同将大坝置于巨型振动台上振动一样。此种方式多适用于坝体结构尺寸和刚度小的情况[6-7]。

对于拱坝和重力坝等混凝土坝，由于混凝土模量与基岩模量的量级相近，研究者已基本形成共识[6，8-26]：在混凝土坝的地震反应分析中应考虑坝体结构和地基的动力相互作用，需要把坝体结构和地基作为整体来分析其地震反应。关于混凝土坝的动力相互作用研究结果表明：坝-基地震反应分析时沿坝基各方向的截取范围取1.0～2.0倍坝高即可满足工程精度要求；考虑坝-基动力相互作用后，混凝土坝的动应力有明显降低，降幅约10%～60%。

在土石坝工程领域，由于早期的坝不高，土石材料的模量与基岩模量相差甚大，因此通常将地基（基岩）视为刚性，采用振动分析方法研究大坝动力反应，即使截取一定范围的地基（不计质量）来分析大坝地震反应，也没有考虑地震的波动效应和无限地基的辐射阻尼影响，在土石坝-地基动力相互作用方面少有研究。但随着我国高土石坝迈入300 m级，其体积和质量巨大，坝-基交界覆盖区域（建基面）沿顺河向长可超千米，河床与两岸高差数百米，地震动输入的非一致性变得更加显著[27]；同时，坝高增加会使坝体底部的模量与基岩的模量的差异减小。在地震中，由坝体产生的散射波会有更多的能量透射至地基向无限域辐射，致使坝-基动力相互作用对高土石坝地震反应的影响增大。因此，高土石坝与地基动力相互作用不容忽视。早期，作者针对高土石坝地震动输入方法及坝-基动力相互作用的影响开展过相关研究[28-35]，部分成果已应用于两河口、托帕、大石峡等高土石坝实际工程[36-38]，但未进行过系统的总结，同时，由于混凝土坝的相关结论可能不适用于土石坝，亟待开展系统深入研究。

本文在自主研发的大型岩土工程有限元分析软件GEODYNA（7.0）[39]中新开发了黏弹性边界单元自动生成和参数识别以及等效荷载计算模块，实现了高效的三维波动分析方法。以我国已建和拟建的若干代表性高土石坝工程为研究背景，采用与实际工程相同的坝体几何参数、筑坝材料参数及设计地震动参数，分别采用传统的振动分析方法和可以考虑坝-基动力相互作用的波动分析方法，通过大量的数值计算和对比分析，系统研究了地基截取范围及坝-基动力相互作用对大坝地震反应的影响，为更加合理地评价高土石坝抗震性能提供了依据。

2 分析方法及软件

2.1 地震反应分析方法目前，对于岩性地基上的高土石坝，普遍采用振动分析方法研究其在地震作用下的动力反应，即将坝基底部边界固定并在计算模型各节点上直接施加地震惯性力。该方法将开放系统的波动问题简化为封闭系统的振动问题，忽略行波效应和河谷地形导致的地震动输入的非一致性，同时忽略地基辐射阻尼的影响，无法反映高土石坝-地基动力相互作用，将可能导致大坝地震反应失真[7]。

联合黏弹性人工边界[40]和等效荷载[41]的波动分析方法[42-44]，能够在较大程度上消除由结构导致的外行散射波，模拟地基的无限域特性，同时可以模拟波动的传播过程和不同河谷地形诱发的非一致地震动输入，从而考虑了坝-基的动力相互作用。这种地震反应分析方法在混凝土坝工程中相对成熟并得到工程界认可[8-9，45]。近年来，该方法已逐渐拓展至地下工程、岩土工程等领域[46-47]，但在土石坝工程领域涉及较少[28-35，48-50]，缺乏系统研究。

2.2 高效的波动分析软件数值模拟作为一种重要的科学研究手段在工程抗震防灾领域得到广泛应用。30多年来，作者致力于高土石坝数值分析方法研究和软件开发，自主研发了大型岩土工程有限元分析软件GEODYNA（7.0）。该软件采用CPU 并行和GPU 加速高性能计算技术，并集成了多场耦合、强非线性、非连续、跨尺度等分析方法，为准确评价大坝抗震性能、优化抗震措施等提供了有效的技术手段。目前，GEODYNA（7.0）已成功服务于30多座高土石坝工程的安全评价与应用研究。

为系统地开展高土石坝-地基动力相互作用研究，基于GEODYNA（7.0）软件平台，实现了高效、全自动的三维波动分析模块，程序的准确性已通过算例验证[29，34]。其主要特色如下：

（1）引入界面单元思想，开发了黏弹性界面单元（图1），替代了传统集中黏弹性人工边界。该单元可在人工截断边界处自动生成，同时避免了集中黏弹性人工边界关于节点代表面积、单元方向等方面的繁琐计算；

（2）开发了黏弹性界面单元参数自动识别技术（图2）。将地震中地基材料实时变化的力学参数传递至相邻的边界单元，不断更新弹簧、阻尼、荷载的参数值，不但适用于岩性地基情况，而且可以实现对非线性覆盖层地基条件辐射阻尼的模拟；

（3）开发了一种波动分析的荷载类型。仅需提供入射波类型、角度和地震动加速度时程，即可完成自由场反应和等效荷载的全自动计算。

图1 黏弹性界面单元与常规黏弹性人工边界

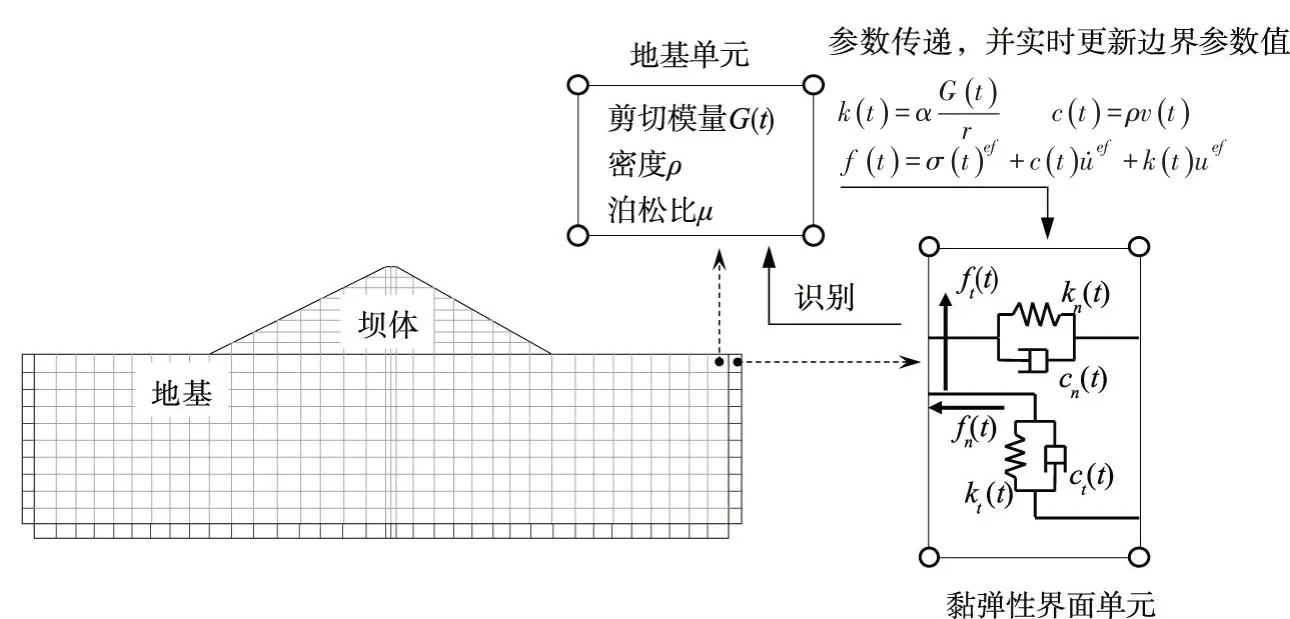
图2 黏弹性界面单元参数自动识别过程

3 地基截取范围的影响

3.1 计算工况在本文研究中，依据紫坪铺（150 m级）、猴子岩（200 m级）、大石峡（250 m级）和如美（300 m级）4个代表性的高土石坝工程，分别参考原工程的坝体几何参数、筑坝材料参数和设计地震动参数（地震加速度时程、峰值等），建立了相应的二维标准坝模型（主要信息见表1），其中坝料采用等效线性黏弹性模型。图3给出了4个二维标准坝模型的有限元计算网格，在网格高度的设定中考虑了坝体模量随高度变化的规律，因此采用逐级变化的分布形式，且在4个模型中自坝顶以下采用同样的网格密度（自坝顶以下0～5 m范围内，每层网格高1 m；在5～25 m范围内，每层网格高2 m；在25～105 m范围内，每层网格高4 m；大于105 m范围内，每层网格高5 m）。岩性地基截取范围（上下游水平向截取长度L与竖向截取深度D）分别取0.3B、0.5B、1.0B和2.0B（B为坝-基交界面顺河向长度），详见图4，边界处的地基网格尺寸设定为10m×10m；假定地基为均匀的线弹性材料，弹性模量10 GPa，密度2650 kg/m3，泊松比0.25。图5给出了本次计算采用的顺河向地震加速度时程曲线，图6为相应的反应谱。采用上述波动分析方法计算岩性地基截取不同范围时坝体的地震反应。

需要指出，本文选定的4 个实际高土石坝工程，其地基均属岩性地基，如地基中含有覆盖层土体，则坝-基动力相互作用影响将更加复杂，研究成果另文发表。

3.2 计算结果与分析为了比较地基上下游水平向截取长度L和竖向截取深度D对坝体地震反应的影响，首先在整体上观察坝体顺河向加速度极值等值线分布规律的差异，然后以大坝断面中心线和坝-基交界面作为特征线，定量地对比加速度分布结果的偏差。

3.2.1 上下游水平向截取长度的影响 首先将基岩的竖向截取深度D固定为1.0B，然后将上下游水平向截取长度L分别取0.3B、0.5B、1.0B和2.0B，对比各工况下大坝顺河向加速度反应。

表1 代表性工程的主要信息

图3 有限元计算网格

图7、图8分别给出了地基截取不同长度时150 m和300 m级大坝断面加速度极值等值线分布，从整体上来看，地基不同截取长度时加速度的分布规律基本一致，差异并不显著，说明上述波动分析方法具有较好的稳定性。

图9、图10 分别给出了各工况下大坝断面中心线位置加速度极值沿坝高的分布及其相对于均值的偏差分布。图11、图12分别给出了部分工况下坝-基交界面加速度沿水平向的分布及其相对于均值的偏差分布。可以看出：各工况下加速度分布规律基本一致，L=0.3B～0.5B时的加速度反应与均值的差异在5%左右，表明该范围具有较高的精度。

3.2.2 竖向截取深度的影响 将上下游水平方向截取长度L固定为1.0B，研究地基竖向截取深度D的影响。D分别取0.3B、0.5B、1.0B和2.0B，对比各工况下大坝加速度反应。

图4 岩性地基截取范围工况示意

图5 顺河向地震加速度时程曲线

图6 顺河向地震加速度反应谱

图7 地基截取不同长度时150m级大坝断面加速度极值等值线（加速度单位：m/s2）

图8 地基截取不同长度时300m级大坝断面加速度极值等值线（加速度单位：m/s2）

图9 地基截取不同长度时大坝断面中心线位置加速度极值分布

图10 地基截取不同长度时大坝断面中心线位置加速度极值相对偏差分布

图11 地基截取不同长度时坝-基交界面加速度极值分布

图13、图14 分别给出了地基截取不同深度时150 m和300 m 级大坝断面加速度极值等值线分布，从整体上来看，地基截取深度对大坝加速度分布的影响要大于截取长度的，但分布规律在总体上仍保持一致。

图12 地基截取不同长度时坝-基交界面加速度极值相对偏差分布

图13 地基截取不同深度时150m级大坝断面加速度等值线（加速度单位：m/s2）

图14 地基截取不同深度时300m级大坝断面加速度等值线（加速度单位：m/s2）

图15、图16分别给出了各工况下大坝断面中心线位置加速度极值沿坝高的分布及其相对于均值的偏差分布。图17、图18分别给出了部分工况下坝-基交界面加速度极值沿水平向的分布及其相对于均值的偏差分布。可以看出：各工况下加速度沿坝高的分布规律基本一致，在坝-基交界面位置的加速度差异略大些，总体上看，D=0.3B～0.5B时的加速度反应与均值的差异在10%以内，表明该截取范围具有较好的精度。

4 二维坝-基动力相互作用的影响

上述研究结果表明：岩性地基各向截取范围为0.3B～0.5B时，计算结果可以满足精度要求。本节在采用波动分析方法来考虑二维坝-基动力相互作用时，地基各方向截取范围取0.5B。计算参数同上节，且同时考虑水平向和竖向地震动；在振动分析时，不考虑基岩，直接约束坝体底边界并施加地震惯性力。以波动分析结果相对于振动分析结果的降幅，即（振动分析结果-波动分析结果）/振动分析结果，来描述两种分析结果量值上的差异，从而说明二维坝-基动力相互作用的影响。

图15 地基截取不同深度时大坝断面中心线位置加速度极值分布

图16 地基截取不同深度时大坝断面中心线位置加速度极值相对偏差分布

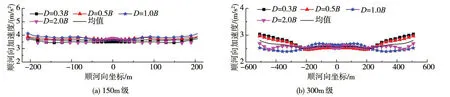
图17 地基截取不同深度时坝-基交界面加速度极值分布

图19 给出了4 个标准坝模型的大坝断面顺河向加速度极值的等值线分布（实线表示振动分析结果，虚线表示波动分析结果），通过与振动分析结果对比可以看出，考虑坝-基动力相互作用后，在地基辐射阻尼的影响下，坝体加速度反应在整体上是减小的，其分布规律也发生一定程度的变化。图20提取了大坝断面中心线位置顺河向加速度极值沿坝高的分布。可见，考虑坝-基动力相互作用后，4个标准坝模型的坝顶加速度极值相比于振动分析结果分别降低31%、38%、46%和45%，同时发现坝顶的“鞭梢效应”略有削弱。

图18 地基截取不同深度时坝-基交界面加速度极值相对偏差分布

图19 大坝断面加速度极值等值线（实线-振动分析，虚线-波动分析，加速度单位：m/s2）

图20 大坝断面中心线位置加速度极值沿坝高的分布

5 三维坝-基动力相互作用的影响

5.1 计算工况在三维条件下，坝-基动力相互作用的影响将变得更加复杂，既包含地基辐射阻尼的影响，还有河谷地形非一致性地震动的影响。本节在讨论三维坝-基动力相互作用时，地基各方向截取范围同样取0.5B。

针对紫坪铺、猴子岩和大石峡三个高土石坝工程，建立相应的简化三维有限元模型，如图21所示；同时，根据古水和拉哇（250 m级）两个工程真实的河谷形状、坝体型式等建立三维有限元模型，如图22所示。在此基础上，分别采用振动分析方法和波动分析方法开展大坝三维地震反应分析，对比大坝的加速度、动位移和面板动应力，讨论坝-基动力相互作用的影响。在振动分析时，不考虑基岩，直接约束坝体外边界并施加地震惯性力；在波动分析时，模拟地震波垂直入射。筑坝材料采用等效线性黏弹性模型，面板和基岩采用线弹性模型，参数依照原工程，计算采用等效线性分析方法。紫坪铺、猴子岩、大石峡、古水和拉哇的顺河向地震加速度峰值分别为0.55g、0.297g、0.365g、0.286g和0.4g，坝轴向加速度峰值与其相同，竖向取其2/3。

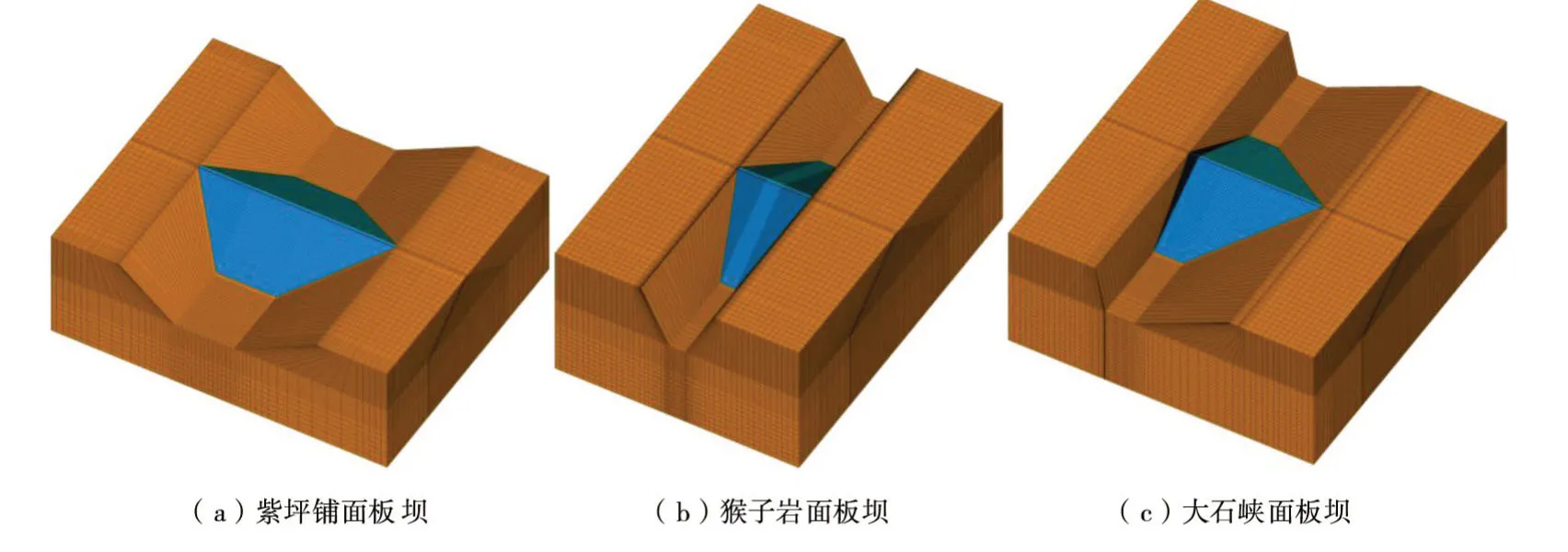
图21 简化的三维有限元模型

图22 实际工程的三维有限元模型

5.2 计算结果与分析

5.2.1 坝体加速度反应 图23给出了简化三维模型的大坝最大断面顺河向加速度极值的等值线分布（实线表示振动分析结果，虚线表示波动分析结果），通过与振动分析结果对比可以看出，考虑坝-基动力相互作用后，在地基辐射阻尼和三维河谷非一致地震效应的综合影响下，坝体加速度反应在整体上是减小的，其分布规律也发生一定程度的变化。图24提取了大坝最大断面中心线位置加速度极值沿坝高的分布，可见，考虑坝-基动力相互作用后，三个简化模型的最大断面坝顶加速度极值相比于振动分析结果分别降低30%、19%和33%，同时发现坝顶的“鞭梢效应”略有削弱。

表2 汇总了三个典型工程简化三维模型的大坝地震反应极值结果。可以看出：相比振动分析方法，考虑坝-基动力相互作用的波动分析方法得到的加速度极值降幅为8%～36%，动位移极值降幅为11%～37%。

对古水和拉哇两个实际大坝模型的加速度和动位移计算结果进行分析。图25为实际大坝最大断面中心线位置顺河向加速度极值沿坝高的分布。加速度和动位移极值汇总于表3中。可以看出：波动分析方法得到的加速度极值降幅为16%～39%，动位移极值降幅为23%～46%，降幅量与三个简化三维模型计算结果范围相差不大。

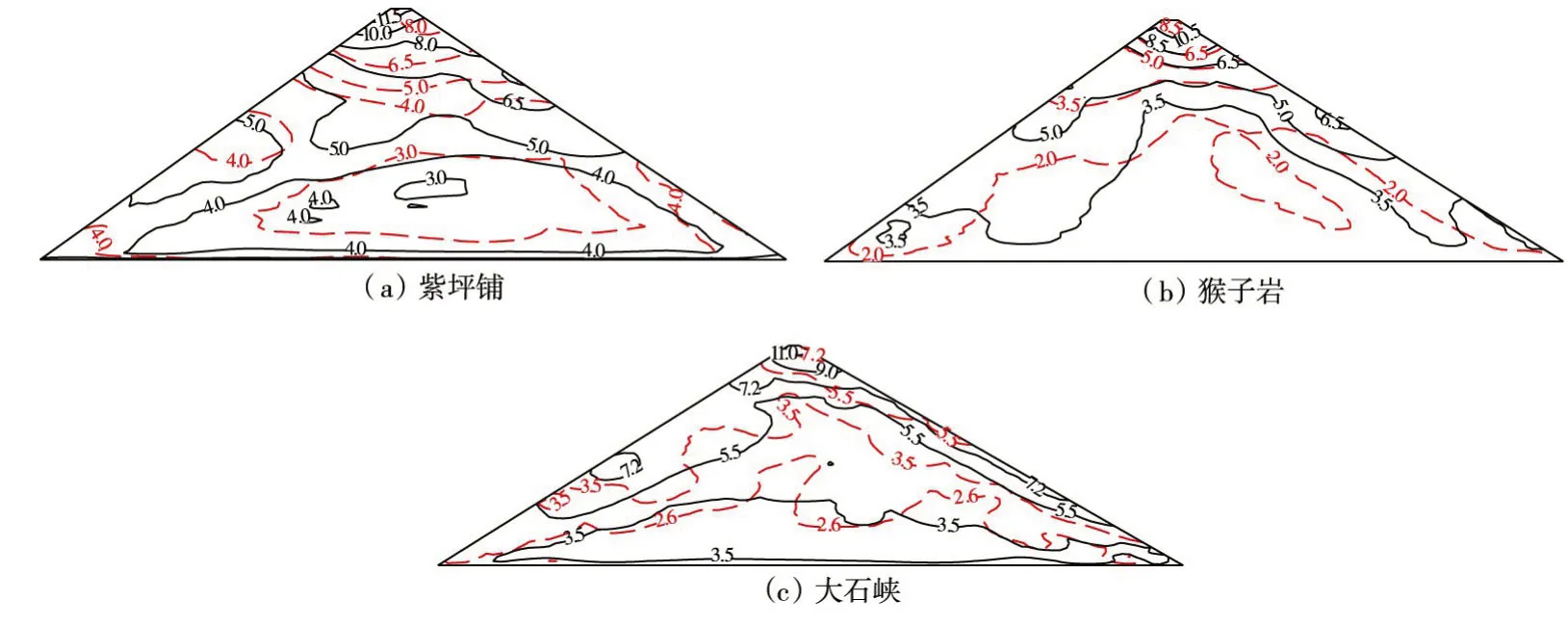
图23 简化三维模型的大坝最大断面加速度极值等值线（单位：m/s2）

图24 简化三维模型的大坝最大断面中心线位置加速度极值沿坝高的分布

表2 简化三维模型的大坝地震反应极值

图25 实际大坝最大断面中心线位置加速度极值沿坝高的分布

表3 古水和拉哇大坝地震反应极值

通过汇总简化坝和实际坝的动力反应结果，可以发现，考虑坝-基相互作用后的加速度极值降幅约为10%～40%，动位移极值降幅约为10%～50%。5.2.2 混凝土面板动应力 图26—图28分别给出了三个简化三维模型坝顶向下游侧最大动位移发生时刻的面板顺坡向动应力分布（负值表示拉应力）。可以看出，在地基辐射阻尼和三维河谷非一致地震效应的综合影响下，考虑坝-基动力相互作用后的面板应力极值明显降低，分布规律也有所变化。从表4 可以看出，波动分析方法得到的面板动应力极值较振动分析方法的降幅：拉应力约为22%～37%，压应力约为15%～30%。

对古水和拉哇两个大坝模型的面板动应力计算结果进行分析。图29和图30分别为整个地震过程中古水大坝面板动压应力与动拉应力极值分布。由图可知，两种分析方法获得的面板动应力整体分布规律及极值位置差别不十分明显。由表5可以看出，与简化坝结论基本一致，波动分析的面板动应力极值较振动分析方法的降幅：拉应力约为27%～41%，压应力约为15%～30%。

图26 紫坪铺面板坝坝顶向下游侧最大动位移发生时刻的面板顺坡向动应力（单位：MPa）

图27 猴子岩面板坝坝顶向下游侧最大动位移发生时刻的面板顺坡向动应力（单位：MPa）

图28 大石峡面板坝坝顶向下游侧最大动位移发生时刻的面板顺坡向动应力（单位：MPa）

表4 简化三维模型的面板动应力极值 （单位：MPa）

图29 古水大坝面板顺坡向动压应力极值（单位：MPa）

图30 古水大坝面板顺坡向动拉应力极值（单位：MPa）

表5 古水和拉哇大坝面板动应力极值 （单位：MPa）

以上结果表明，坝-基动力相互作用的影响十分明显，振动分析方法不能准确反映大坝地震反应实际情况，高土石坝抗震分析采用大坝-地基体系的波动分析方法是十分必要的。

6 结论

本文通过在大型岩土工程有限元分析软件GEODYNA（7.0）中开发了黏弹性边界单元自动生成、参数识别和等效荷载计算模块，实现了高效的三维波动分析方法。在此基础上，以若干代表性高土石坝为工程背景，分别采用波动分析方法和传统的振动分析方法，系统研究了考虑坝-基动力相互作用对大坝地震反应的影响。结果表明：

（1）波动分析方法能很好地反映地震波传播过程、无限地基的辐射阻尼效应以及地震动输入的非一致性，避免了传统振动分析方法导致的能量封闭和河谷边界加速度的一致性问题。因此，高土石坝地震反应采用波动分析方法更加符合实际。

（2）考虑岩性地基与高土石坝动力相互作用时，建议岩性地基上下游水平向截取长度L与竖向截取深度D取为0.3B～0.5B（面板坝时约1.0H～1.5H，心墙坝时约1.2H～1.8H，H表示坝高），其计算结果的偏差在工程可接受范围内。

（3）即使在岩性地基条件下，坝-基动力相互作用的影响也是明显的。若干代表性工程计算结果表明：与振动分析方法相比，波动分析方法计算得到的坝体加速度极值降幅约为10%～40%，动位移极值降幅约为10%～50%，面板动应力极值降幅：拉应力约为20%～40%，压应力约为15%～30%。振动分析方法明显高估大坝的反应，将可能低估大坝的极限抗震能力，不利于评价大坝在极端地震条件下的真实性态。