等分法———求匀强电场的E 和φ 的“金钥匙”

■江苏省六合高级中学 傅明峰

在与电场相关的高考试题中,经常出现要求求解电场中某点的电势或电场强度的问题。这类问题虽然是常见的,但往往会因为设置的情景较新,所要求解的问题距离给出的信息较大,而使不少同学在解答时感到茫然。下面我们介绍一种方法,简称“等分法”。这种方法通过捕捉信息和几何作图,先找出电场中关键点的电势,再确定等势线或等势面,最后根据电场线垂直于等势面的特点,以及电场强度和电势差的关系来求解。

例题(2017·全国Ⅲ卷)一匀强电场的方向平行于x O y平面,平面内a、b、c三点的位置如图1所示,三点的电势分别为10V、17V、26V。下列说法中正确的是( )。

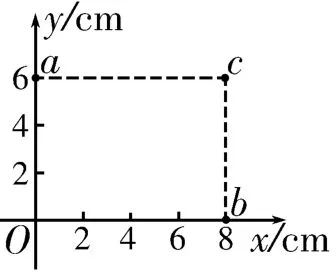
图1

A.电场强度的大小为2.5V/cm

B.坐标原点O处的电势为1V

C.电子在a点的电势能比在b点的低7e V

D.电子从b点运动到c点,静电力做功为9e V

审题：在匀强电场中将某一线段等分的同时就将该线段两端的电势差等分。在匀强电场中,因为电场线平行且均匀分布,所以等势线平行且均匀分布。以上两点是解决此类问题的“金钥匙”。

解析：由题意知φa=10V,φb=17V,φc=26V,则a b连线与O c连线交点的电势满足,故φO=φa+φb-φc=1V,选项B正确。从a点到b点移动电子,静电力做功W=-e Ua b=7e V,静电力做正功,电势能减小,故电子在a点的电势能比在b点的高7e V,选项C错误。从b点到c点移动电子,静电力做功W'=-e Ub c=9e V,选项D正确。如图2所示,过b点作b d垂直于O c,由几何关系得xc d=故解得d点的电势φd=17V,即b d为等势线,从而得电场线沿c O方向,电场强度2.5V/cm,选项A正确。

答案：A B D

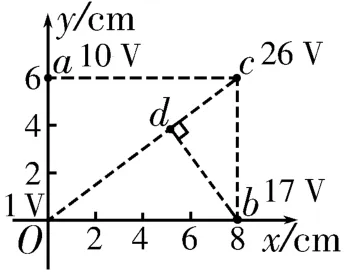
图2

(1)等分法的两个有用的推论：①在匀强电场中,沿任意一条直线电势降落都是均匀的；②在匀强电场中,相互平行且相等的线段两端点的电势差相等。

(2)运用等分法解题的步骤：①确定所给点中电势最高点和最低点,用直线连接；②根据第三点的电势值,将①中的直线平分为等距离的n段；③找到直线上与第三点电势相同的第四点,连接第三和第四点所得直线即为等势线；④作出垂直于等势线的直线,并根据电势降落的方向在新作的直线上加上箭头,画出电场线,再根据E=求出电场强度的大小。

1.运用等分法确定匀强电场的方向和场强E。

变式1：A、B、C是匀强电场中的三个点,各点电势分别为φA=10V、φB=2V、φC=6V,A、B、C三点在同一平面上。如图3所示的四幅关于A、B、C三点的位置及电场强度的方向表示正确的是( )。

图3

审题：在匀强电场中,电场强度大小处处相等,方向处处相同,则电场线是平行且等间距的,电势沿着电场线逐渐降低,电场线与等势面垂直。

解析：根据φA=10V、φB=2V、φC=6V可知,AB连线的中点M的电势为6V,因此M点与C点的连线为等势面,与MC连线垂直的线即为电场线。又因为电势沿着电场线逐渐降低,所以D图正确。

答案：D

变式2：A、B、C是匀强电场中平行于电场线的某一平面上的三个点,各点的电势分别为φA=5V,φB=2V,φC=3V,H、F三等分A B连线,G为A C连线的中点。如图4所示的四幅示意图中,能正确表示电场强度方向的是( )。

图4

审题：根据匀强电场中电势、电场线、等势线和电场强度的特点,在A B连线上找出电势与C点电势相等的点,即可得到一条等势线,进而可以作出电场线。

解析：把A B连线三等分,因为UA B=3V,所以每等份两端的电势差为1V,即φH=4V,φF=3V,则直线F C为等势线,电场线应垂直于F C,且从电势高处指向电势低处,C图正确。把AC连线两等分,因为UAC=2V,所以每等份两端的电势差为1V,即φG=4V,则直线GH为等势线,电场线应垂直于HG,且从电势高处指向电势低处,B图正确。

答案：B C

变式3：如图5所示,匀强电场的方向平行于xOy坐标系平面,坐标原点O处的电势为2V,a点的坐标为(0cm,4cm),电势为8V,b点的坐标为(3cm,0cm),电势为8V,则电场强度大小为( )。

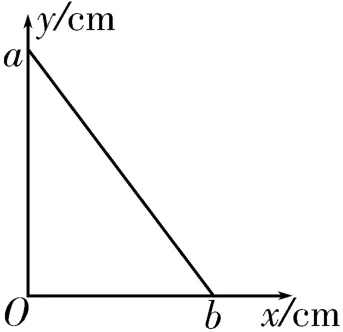
图5

A.250V/m

B.200V/m

C.150V/m

D.120V/m

审题：根据题中数据可知,a、b两点的电势相等,先运用几何关系求出O点到a b连线的距离,再由匀强电场中电势差与电场强度的关系U=E d,即可得出电场强度的大小。

解析：由题意可知,a、b两点的电势相等,则a b连线为一条等势线,又有O点电势为2V,则匀强电场的场强方向垂直于a b连线指向左下方。过O点作a b连线的垂线交a b于c点,如图6所示,由几何关系得t a n则∠b=53°。O c=O b·sin ∠b=0.03m×sin53°=2.4×10-2m。c、O两点间的电势差U=8V-2V=6V,因此电场强度大小

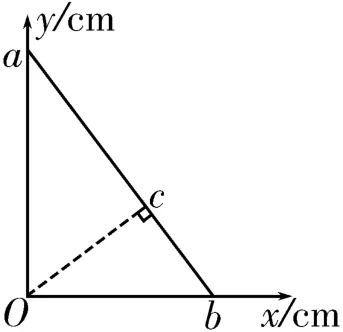
图6

答案：A

2.运用等分法求匀强电场中各点的电势大小。

变式4：a、b、c、d是匀强电场中的四个点,它们正好是一个矩形的四个顶点。电场线与矩形所在平面平行。已知a点的电势为20V,b点的电势为24V,d点的电势为4V,如图7所示。由此可知c点的电势为( )。

A.4V B.8V

C.12V D.24 V

审题：依据在匀强电场中将某一线段等分的同时就将该线段两端的电势差等分,将b d五等分,找到与a点电势相等的点e,连接a e,由c f∥a e,找到与c点电势相等的点f,即可求得φc。

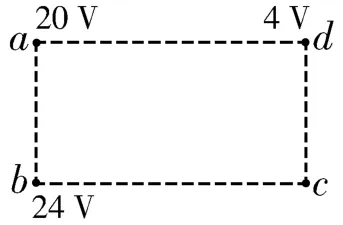
图7

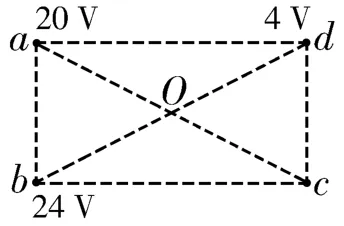
图8

解法一：(推论①)连接对角线a c和b d相交于O点,如图8所示。由匀强电场的性质得φO=解得φc=8V。

解法二：(推论②)因为a b=c d且a b∥c d,所以φb-φa=φc-φd,解得φc=8V。

答案：B

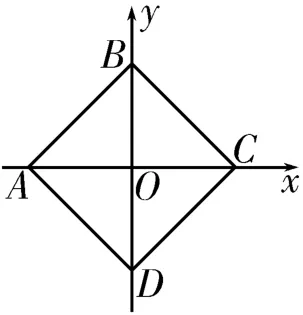
图9

变式5：如图9所示,在x O y坐标系中有以O点为中心、边长为0.2m的正方形,顶点A、B、C、D分别在坐标轴上。在该平面内有一匀强电场(图中未画出),已知A、B、C三点的电势分别为3V、-V、-3V。则下列说法中正确的是( )。

A.D点的电势为V

B.该电场的场强大小E=10V/m

C.该电场的场强大小E=10V/m

D.电场方向与x轴正方向间的夹角为30°

审题：依据匀强电场的特点,运用对称思想可求得D点的电势。依据U=E d可求解场强问题。

解析：根据A、C两点的电势分别为3V、-3V可知,O点的电势为零,由对称性可知D点的电势为V,选项A正确。设过O点的等势线与x轴间的夹角为α,则E解得α=60°,E=10V/m,选项B错误,C正确。因为电场线与等势线互相垂直,所以电场方向与x轴正方向间的夹角为30°,选项D正确。

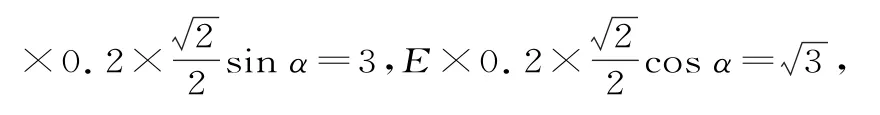
答案：A C D

1.如图10所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则电场强度的大小为( )。

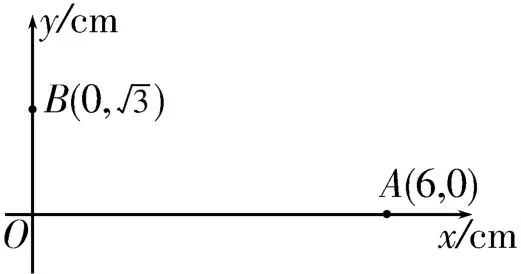
图10

2.如图11所示,以O点为圆心,以R=0.20m为半径的圆与坐标轴交点分别为a、b、c、d,该圆所在平面内有一匀强电场,场强方向与x轴正方向间的夹角θ=60°,已知a、b、c三点的电势分别为4V、4V、-4V,则下列说法中正确的是( )。

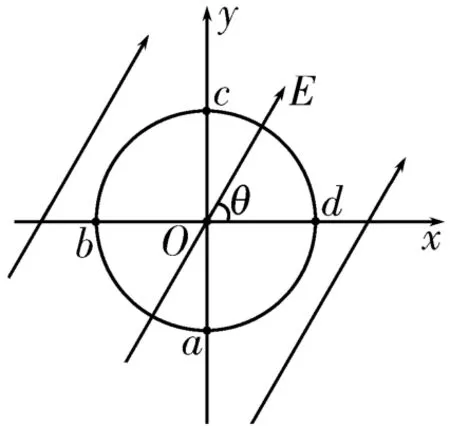
图11

A.该匀强电场的场强E=40V/m

B.该匀强电场的场强E=80V/m

C.d点的电势为-2V

D.d点的电势为-4V

3.如图12所示,水平面内有A、B、C、D、E、F六个点,它们均匀分布在圆心为O、半径R=2 cm的同一圆周上,空间有一方向与圆平面平行的匀强电场。已知A、C、E三点的电势分别为φA=(2-)V、φC=2 V,φE=(2+)V,则下列判断中正确的是( )。

图12

A.电场的方向由A点指向D点

B.电场强度的大小为100V/m

C.该圆周上的点电势最高为4V

D.将电子沿圆弧从D点移到F点,静电力始终做负功

参考答案：1.A 2.D 3.B C