不同振动特性参数对杏树振动响应的影响
2019-02-25杨会民散鋆龙陈毅飞王学农牛长河侯书林
杨会民,散鋆龙,陈毅飞,王学农,牛长河,侯书林
不同振动特性参数对杏树振动响应的影响
杨会民1,散鋆龙2,陈毅飞1,王学农1※,牛长河1,侯书林2
(1. 新疆农业科学院农业机械化研究所,乌鲁木齐 830091;2. 中国农业大学工学院,北京 100083)
为研究振动时间、振动频率和振动激励点振幅等不同振动特性参数对杏树振动的影响,该文利用ANSYS软件对杏树进行了有限元建模分析;通过三因素三水平试验分析不同振动特性参数对杏树振动检测点的影响,利用Design Expert软件进行优化分析,并进行实验室验证试验。杏树自由模态振动响应分析表明最佳杏树振动采收响应频率范围为0~20 Hz;谐振动响应分析可知在最佳频率范围内,杏树振动激励点振幅为5、10和15 mm时,同一频率下,随着激励振幅的增大,相同位置加速度增大,但振动曲线整体变化规律和趋势一致。试验分析可知,各因素影响检测点1和2加速度的强弱顺序一致:激励点振幅>振动频率>振动时间;各因素影响检测点3加速度的强弱顺序为:振动时间>激励点振幅>振动频率;建立3个检测点的响应方程,由下至上3个检测点的回归方程决定系数分别为0.906 7、0.879 3和0.973 3;多目标参数优化结果为:振动时间7.207 s,振动频率15 Hz,激振点振幅10 mm,通过验证试验可知由下至上各检测点加速度为10.4、10.2和9.3,与优化值相近。该研究可为杏振动采收机械参数设计提供参考。
振动;收获;机械化;杏;振动响应试验
0 引 言
杏(Lam.)属蔷薇科()杏属(Mill.)落叶乔木,是世界重要的经济果树之一[1]。中国杏树栽培历史悠久,根据遗传学研究表明,新疆伊犁河北岸野生普通杏是世界栽培杏的起源种群[2]。截止2016年底,新疆维吾尔自治区杏树种植面积12.487万hm2,产量115.42万t[3]。近年来新疆杏产业化发展迅速,但其收获方式仍停留在利用长梯或长杆辅助的传统人工采摘,作业风险较高,同时增大了收获成本,收获环节成为制约新疆林果产业发展的首要问题。振动采收是目前林果采收的主要手段之一,利用机械化采收方式可有效降低劳动成本,提高林果采收效率。
国外已形成了一套完整的林果振动采收体系,林果振动采收理论完善,机具成熟,其中不同振动采收参数对林果收获的影响是主要的研究方向之一[4-11]。由于果树自身生长特性与材料特性,不同品种果树的振动响应不同,采收机械振动频率、振幅、振动时间以及振动激励点位置等振动特性参数的选择和设定将直接影响林果采收效率与质量[11-12]。早在1957年美国就已展开往复式振动采收机工作频率和振幅对李子采收、果实损伤以及果树摇动所需动力的研究[13-14]。Aristizábal等[15]研究使用圆周和多方向振动采收咖啡过程中,振动频率、振幅、振动时间以及振动激励位置对成熟果实采收率的影响。Polat等[16]为获得巴丹木最佳振动采收参数,利用惯性式悬臂振动机进行振动采收,研究相同振动时间下,不同振动频率和振幅参数组合对果实脱落率的影响。
国内开展了大量林果振动采收机构设计、振动传递特性以及果树响应状态等方面的基础研究,但对振动特性参数对林果采收影响研究较浅[17-26]。范雷刚等[27]研究了海棠果树受不同振动特性参数组合时,不同位置加速度变化。杜小强等[28]对所设计的三维激振林果采收机构进行优化设计,并对系统振动响应进行了分析。王东等[29]利用有限元进行果树响应分析,研究不同树形果树振动响应状态。
为研究不同振动采收参数对林果机械采收的影响,指导杏林果振动采收机械设计,优化杏振动采收机械性能,本文利用ANSYS建立杏树有限元模型,进行杏树自由模态与谐响应仿真分析,确定杏振动采收参数范围。在实验室内进行振动试验,分析振动试验结果,研究不同振动特性参数组合对振动采收的影响,得到杏最佳振动参数组合,并进行实验室验证试验,以期为杏振动采收机械参数设计提供设计及理论依据。
1 杏振动采收机理
根据4GZG-25型牵引式偏心式林果采收样机工作方式与振动特性,建立偏心块对称放置的振动采收机-果树模型,如图1所示[30-31]。在振动采收机与杏树加持位置水平面上,以杏树夹持位置中心为坐标系原点,方向为系统水平运动方向,方向为与水平垂直运动方向。杏树动力学特性由加持位置杏树树干等效弹性系数(常数)与等效阻尼系数(常数)表示。
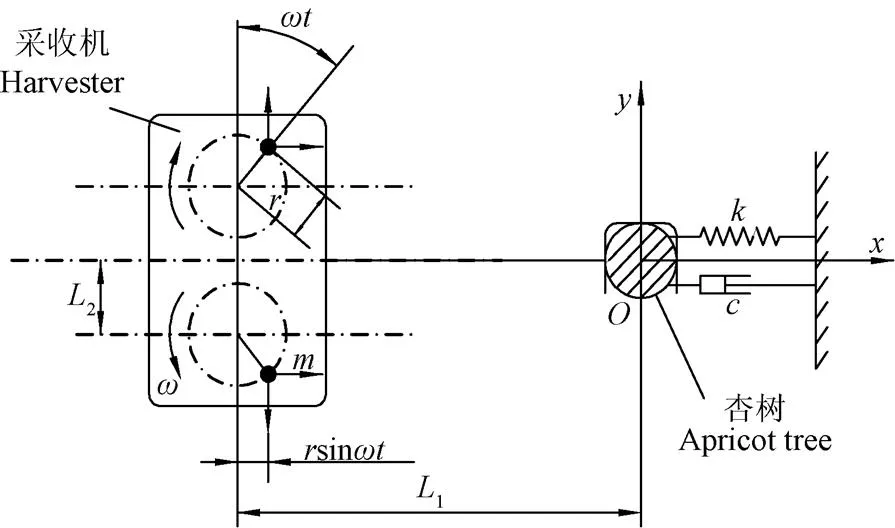
注:m为偏心块质量,kg;ω为角速度,rad·s-1;t为时间,s;L1为振动箱与杏树间距离,m; L2为偏心块旋转轴中心与x轴间距离,m;r为偏心块转动中心与质心的距离,mm;k为杏树树干等效弹性系数,常数;c为杏树树干等效阻尼系数,常数。
对称放置的2个偏心块质量相等,转动方向相反,结合杏树-振动机动力学模型,由牛顿第三定律可知,由于偏心块做圆周运动,采收机振动过程中偏心机构整体在方向产生的力相互叠加,在方向上的力相互抵消,即方向受力为零。由此可的偏心块产生的惯性力为
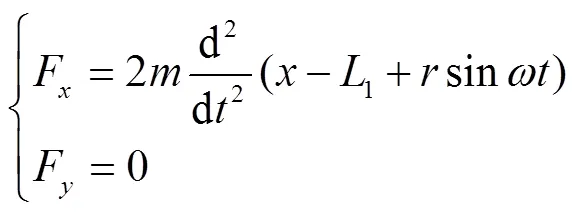
式中F为偏心机构方向上产生的力,N;F为偏心机构方向上产生的力,N;为偏心机构在方向上的位移,mm。
对系统整体进行受力分析,并简化可得杏树-振动采收机振动微分方程为
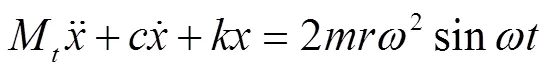

2 杏树振动响应试验材料与方法
由于所设计的4GZG-25型牵引式偏心式林果采收样机正弦振动激励输出特性,为优化样机工作参数提供参考,研究杏树受迫振动后的响应状态,获得最佳的振动响应参数;通过有限元建模与实验室振动响应试验相结合对杏树振动响应进行研究,对优化后的参数进行实验室验证试验。杏树振动响应试验路线如图2所示。
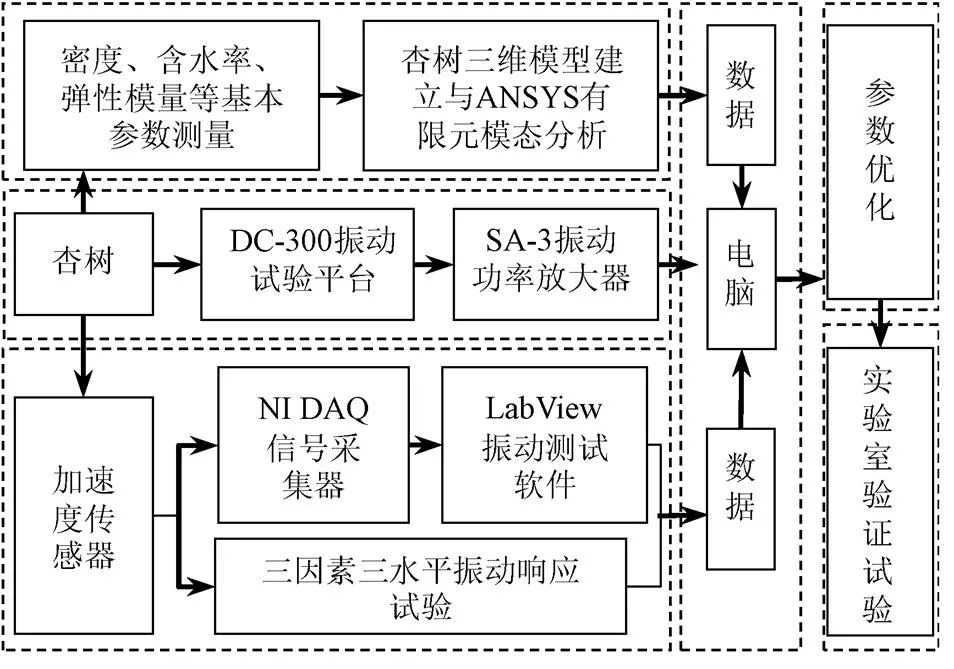
图2 杏树振动响应试验路线
根据牛顿第二定律,振动过程中杏果实在质量一定的情况下,加速度越大,果实由于惯性产生的脱落力越大。因此本文以杏树检测点处加速度为主要评价指标进行试验,加速度单位为(为重力加速度,取9.8 m/s2)。
2.1 试验材料
以新疆主要杏品种库麦提杏树为主要研究对象,树形结构为自然开心型[29]。2018年6月底杏成熟期,将新疆农业科学院轮台国家果树资源圃内树龄为3 a的果树,移栽到新疆农业科学院农业机械化研究所物料特性实验室内,进行测绘与基本参数测量。
2.2 试验仪器与软件
试验仪器:苏州试验仪器设备公司DC-300振动试验台,正弦推力2.94 kN,工作频率5~5 000 Hz,最大位移40 mm;SA-3振动平台功率放大器,额定输出功率15 kVA;YMC压电式IEPE型加速度传感器,灵敏度50 mV/ms2,测试范围±10,频率范围0~4 000 Hz。美国NI公司NI DAQ 9 178四通道信号采集器,NI 9 234振动信号采集卡。上海一恒科学仪器有限公司BPG-9 140A型精密鼓风干燥箱,功率2 050 W,温度范围RT+10~25 ℃。美特斯工业系统(中国)有限公司CMT 6 103系列电子万能试验机,最大应力1 kN。
试验软件:ANSYS Workbench 17.0有限元分析软件;SolidWorks 2017三维建模软件;Labview振动测试虚拟软件;Design expert 10.0.3试验分析软件。
2.3 试验方法
利用SolidWorks 2017软件对已测绘的杏树进行三维建模,使用ANSYS Workbench 17.0软件对杏树进行有限元分析,有限元模型如图3所示。分析杏树不附加任何振动激励状态下的自由模态,结合模态云图仿真结果中杏树响应的一致性,获得最佳的振动频率范围;研究杏树不同振幅下受正弦振动激励时沿树干3个检测位置的谐响应状态,每个检测位置间距离为400 mm,以加速度大小表示检测位置的响应状态。
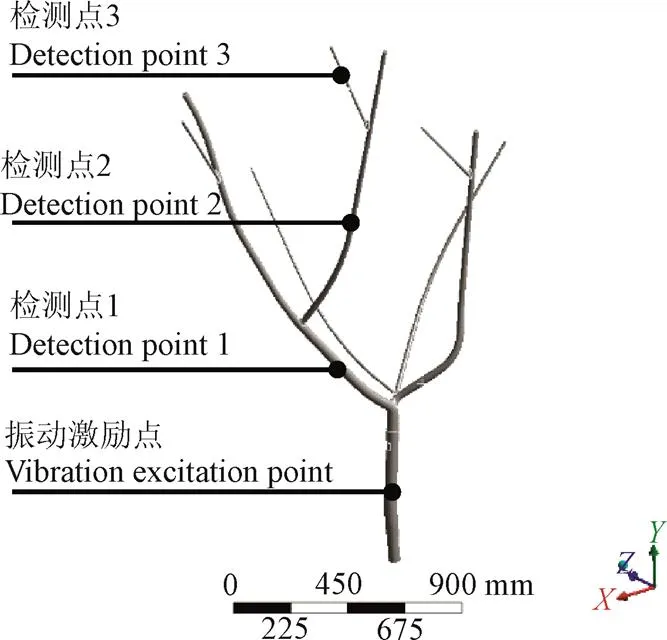
图3 杏树有限元模型
根据有限元分析相应结果,利用DC-300振动实验平台对杏树施加正弦振动激励,研究振动时间、振动频率和加持点振幅等振动采收主要因素对杏树不同位置加速度的影响。杏树从果园中砍伐后立即移入实验室,如图4所示。去掉细小树枝与树叶,利用自制的连接器将杏树与振动平台连接,杏树根部固定。沿杏树树干安装加速度传感器,传感器安装位置与有限元分析时果树3个检测点位置相同,通过Labview振动检测软件得到NI DAQ 9 178振动信号采集器所采集的加速度数据。采用Design Expert 10.0.3 软件进行试验方案设计,分析杏树不同位置在不同振动激励参数下的响应状态,得到最佳的振动激励参数,并进行实验室验证试验。

图4 杏树振动检测平台
3 杏树有限元建模与分析
根据国家标准GB/T 1 931-2009木材含水率测定方法和GB/T 1 936.2-2009木材抗弯弹性模量测定方法测得库麦提杏树木材含水率为41.01%,弹性模量为425.35 MPa,密度为0.856 g/cm3,泊松比取0.330,由此可得杏树木材剪切模量为159.9 MPa。将所测得的杏树木材基本参数代入ANSYS Workbench建立的杏树模型中,对杏树进行有限元分析。
3.1 杏树自由振动模态分析
利用ANSYS Workbench中Modal模块对杏树进行1~50阶模态分析,得到反应杏树模型自由模态下阶次、响应频率和杏树整体形变关系的3D曲面图,如图5所示。
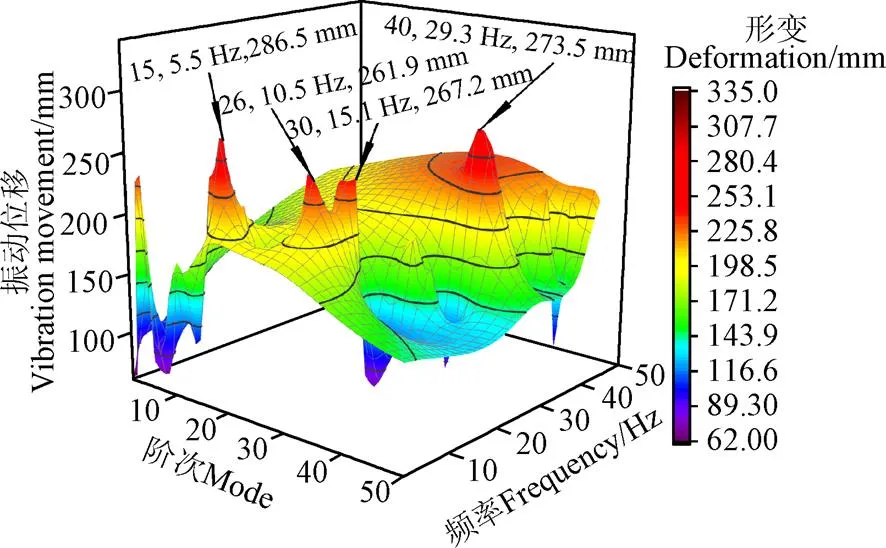
图5 杏树自由模态响应分析
由图5可知,杏树在15、26、30和40阶时具有典型自由模态响应,对应的频率分别为5.5、10.5、15.1和29.3 Hz,果树最大形变分别为286.5、261.9、267.2和273.5 mm。
分析杏树典型自由模态云图6可知,第15和26阶典型自由模态中杏树枝干末端响应性较高;第30阶果树整体响应一致性高,杏树末端形变响应最大;第40阶29.3 Hz时果树部分枝条变形严重,树形整体结构易被破坏。由此可知:杏树振动采收过程中最佳频率范围可控制在5~15 Hz之间。
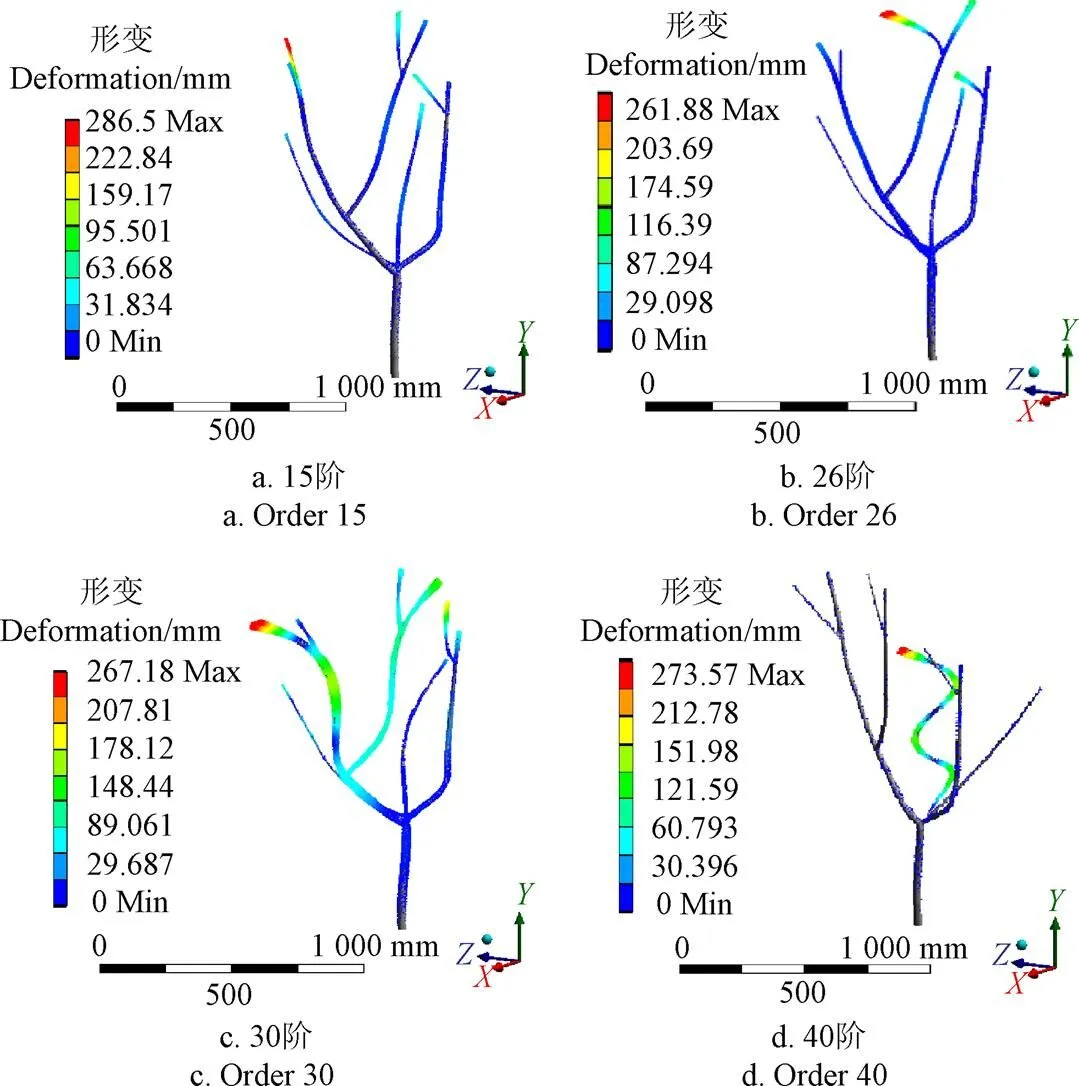
图6 杏树典型模态响应云图
3.2 杏树谐振动响应分析
通过对杏树模型进行谐响应分析,确定杏树枝干在固定幅值的正弦位移作用下的稳定响应,采用完全法进行求解。根据果树振动采收激振点振幅特性[31],夹持点振幅设定为5、10和15 mm进行杏树谐振动响应分析。由自由模态仿真结果设定频率范围为0~20 Hz,进行谐振动分析可得到检测点1、2、3位置加速度值变化曲线,如图7。

图7 不同振幅激励下检测点X轴方向加速度变化曲线
由图7可知,激励点振幅为5、10和15 mm时,在0~20 Hz振动频率区间内,检测点1在4.67、7.33、15.33和18.66 Hz时具有典型加速度峰值;检测点2在6.34和17.33 Hz时具有典型加速度峰值;检测点3在7.01和17.3 Hz时具有典型加速度峰值。检测点位置由下至上,振幅为5 mm时,最大加速度分别为7.52、6.57和4.93;振幅为10 mm时,最大加速度分别为14.89、12.96和9.87;振幅为15 mm时,最大加速度分别为22.36、19.71和14.8。
由此可知,在0~20 Hz内,振幅为5、10和15 mm时,同一频率下,随着激励振幅的增大,相同位置加速度增大,但振动曲线整体变化规律和趋势一致。
4 杏树实验室振动试验
为了验证有限元分析结果,获得最优振动采收参数组合,指导振动采收样机参数设计,根据样机工作原理与ANSYS有限元仿真结果,在2018年6月底在新疆农业科学院农业机械化研究所物料特性实验室中,按照试验路线图2,利用振动试验平台对刚移栽入实验室的成熟期杏树施加振动激励,进行振动试验,试验数据由加速度传感器与NI 9 234振动信号采集卡采集。
4.1 评价指标
选择振动时间(s)、激励点振幅(mm)和振动频率(Hz)3个试验因素,在实验室进行振动试验,每组试验重复3次。树枝加速度是果实振动脱落的主要评价指标,本文选择3个主要检测点所测得的加速度作为评价指标。
4.2 振动试验设计
进行三因素三水平组合试验,根据杏树有限元自由模态响应与谐振动响应分析结果,试验因素与水平编码如表1所示。
利用Design Expert 10.0.3 软件进行试验方案设计,共进行17组试验,每组重复3次,试验结果取平均值,试验数据如表2。
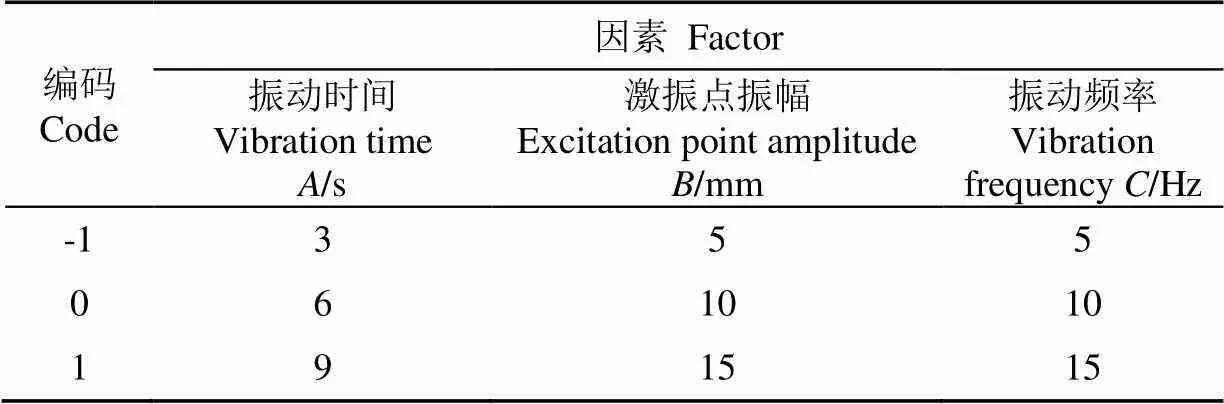
表1 试验因素和水平编码
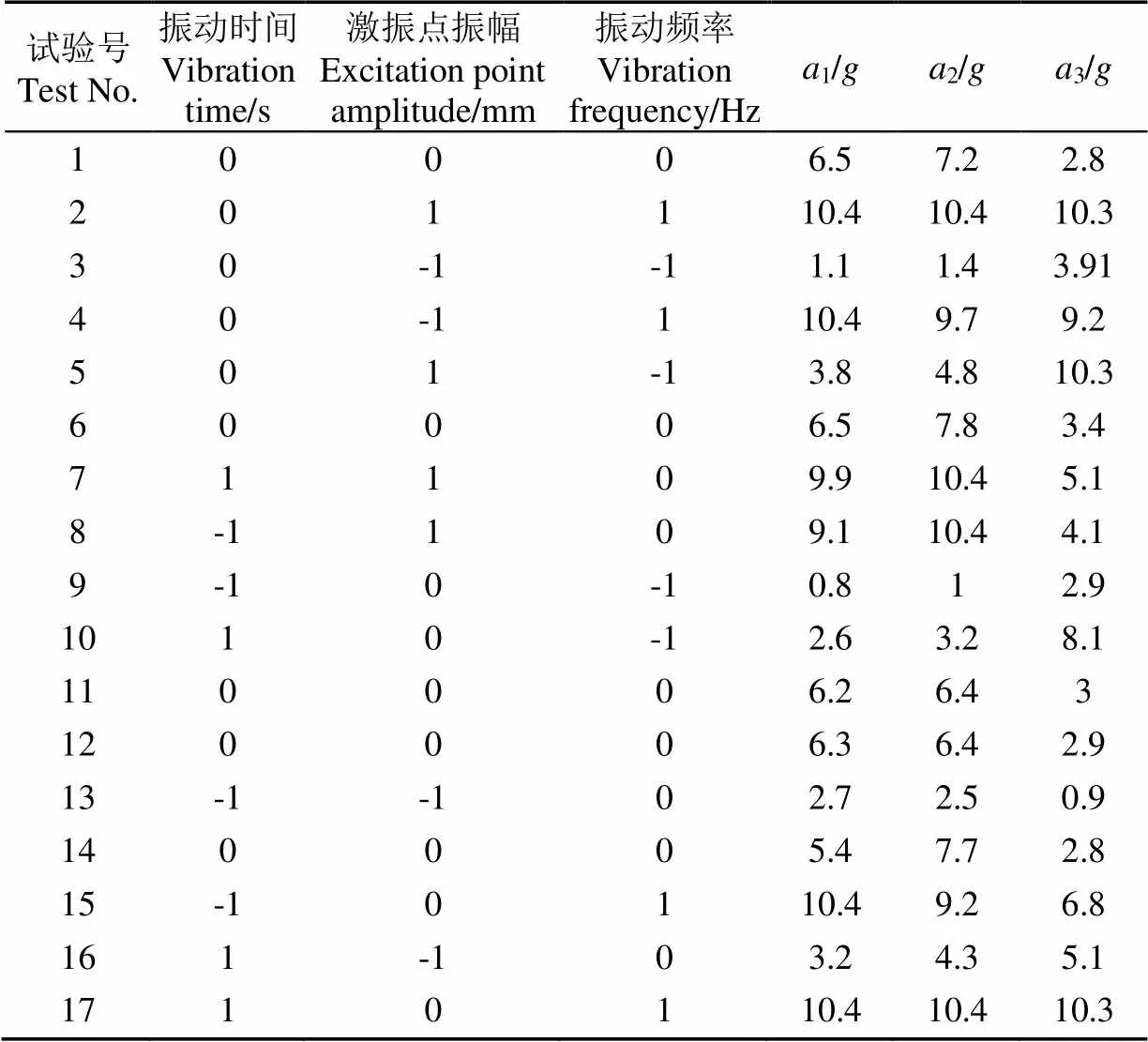
表2 试验设计方案及响应值结果
注:1、2、3为图3中3个检测点的加速度。
Note:1,2, and3are the accelerations of the three detection points in Fig.3.
4.3 试验结果分析与回归模型建立
通过Design Expert 10.0.3软件对试验结果进行回归分析,并进行多元回归拟合,得到3个检测点加速度1、2和3,3个试验指标的回归方程,并验证其显著性,试验分析结果如表3所示。
4.3.1 检测点1加速度的显著性分析
由表3可知,整体模型极其显著(<0.01),各因素影响检测点1加速度的强弱顺序为;其中模型回归项和显著,因素不显著(>0.05)可忽略,拟合后得到回归方程决定系数2为0.906 7,拟合程度高,方程为
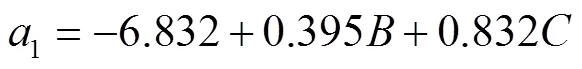
式中为激励点振幅,mm;为振动频率,Hz。
4.3.2 检测点2加速度的显著性分析
由表3可知,整体模型极其显著(<0.01),各因素影响检测点2加速度的强弱顺序为>>,与检测点1一致,其中模型回归项和显著,因素不显著(>0.05)可忽略,拟合后得到回归方程决定系数2为0.879 3,方程为
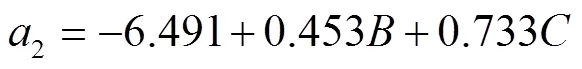
4.3.3检测点3加速度的显著性分析
由表3可知,整体模型极其显著(<0.01),整体模型极其显著,各因素影响检测点3加速度的强弱顺序为>>。其中除模型回归项、与2的检测点3加速度值大于0.05不显著可忽略,其他回归项均为显著。由于检测点3位于整个果树末端,检测点位置、振动过程中位移、果树树枝粗细以及果果枝形状等原因会造成因素对不同检测点的影响强弱顺序不同。回归方程决定系数2为0.973 3,拟合程度极高,方程为
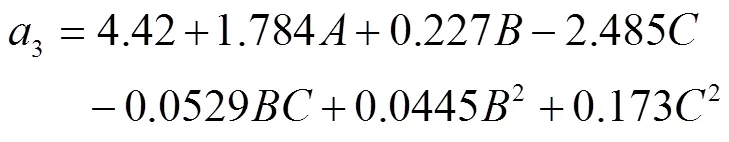
式中为振动时间,s。
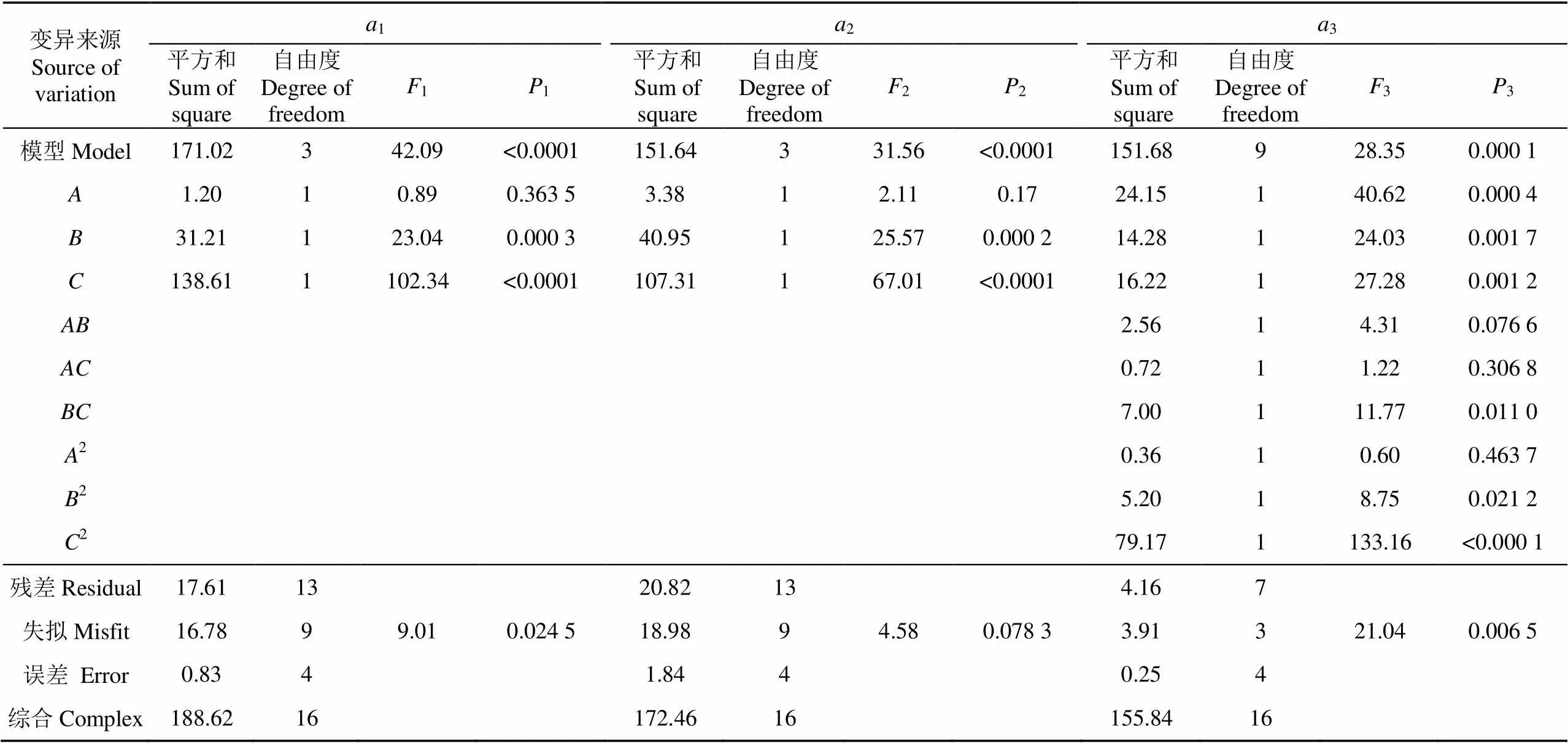
表3 检测点加速度回归模型方差F检验与分析
注:<0.01,为极其显著;0.01<<0.05为显著。
Note:<0.01, extremely significant; 0.01<<0.05, significant.
4.4 各项振动特性参数优化
振动过程果实脱落的响应加速度越大,果实所受脱落力越大,果实更易脱落,即3个检测点加速度响应均为最大值时满足优化条件。根据上述有限元分析结果、振动试验与项目组前期的试验结果[30-31],为避免振动过程造成果树损伤,3个检测点加速度优化范围为0~20;根据检测点由下至上所处的位置,设定3个检测点值的权重,检测点1、2设置权重为1,检测点3接近果实生长位置权重为2。
根据上述参数设定,由Design Expert10.0.3软件中Optimization模块(响应优化)对检测点进行多目标优化。
目标编码变量优化函数为

对目标函数进行优化得到最优振动采收参数组合为:振动时间7.207 s,振动频率15 Hz,激振点振幅10 mm。
4.5 实验室验证试验
为验证最终优化参数,按优化后得到参数调整振动实验平台设置参数,在实验室中进行振动试验,试验重复3次取平均值,优化值与实际测量值之间分析验证结果如表4所示,实验值与优化参数相近,偏差较小。
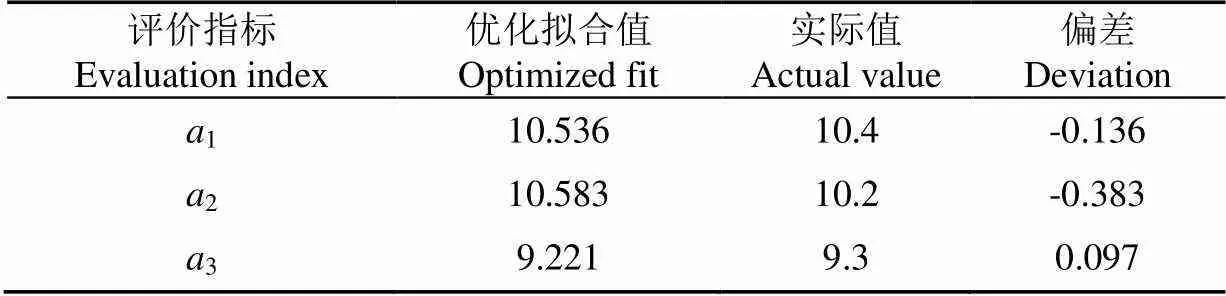
表4 优化值与实际值对比结果
5 结 论
1)对建立的杏树模型进行ANSYS有限元分析,通过杏树自由模态振动响应分析可知最佳杏树振动采收响应频率范围为0~20 Hz;通过谐振动响应分析可知在0~20 Hz内,杏树振动激励点振幅为5、10和15 mm时,同一频率下,随着激励振幅的增大,相同位置加速度增大,但振动曲线整体变化规律和趋势一致。
2)研究杏树振动特性参数(振动时间、激励点振幅和振动频率)对不同检测点振动加速度的影响规律,进行三因素三水平试验分析,各参数对检测点1和2的影响强弱顺序一致为>>;对检测点3的影响强弱顺序为>>。
3)建立3个检测点响应方程,由下至上3个检测点的回归方程决定系数分别为0.906 7、0.879 3和0.973 3,为杏树振动特性分析提供参考。
4)利用Design Expert10.0.3软件响应优化模块对检测点响应方程进行优化,获得最优振动采收参数组合为:振动时间7.207 s,振动频率15 Hz,激振点振幅10 mm,经试验验证可知由下至上3个检测点加速度分别为10.4、10.2和9.3,试验值与优化参数相符,该研究可为杏振动采收机械参数设计提供设计及理论依据。
[1] 包文泉,乌云塔娜,王淋,等. 野生杏和栽培杏的遗传多样性和遗传结构分析[J]. 植物遗传资源学报,2017,18(2):201-209.
Bao Wenquan, Wuyun Tana, Wang Lin, et al. Genetic diversity and population structure of the wild apricot and cultivation apricot[J]. Journal of Plant Genetic Resources, 2017, 18(2): 201-209. (in Chinese with English abstract)
[2] 廖康. 新疆野生果树资源研究[M]. 乌鲁木齐:新疆人民出版社,2013.
[3] 中华人民共和国国家统计局. 中国统计年鉴[M]. 北京:中国统计出版社,2017.
[4] BlancoRoldán G L, GilRibes J A, Kouraba K, et al. Effects of trunk shaker duration and repetitions on removal efficiency for the harvesting of oil olives[J]. Applied Engineering in Agriculture, 2009, 25(3): 329-334.
[5] Pezzi F, Caprara C. Mechanical grape harvesting: Investigation of the transmission of vibrations[J]. Biosystems Engineering, 2009, 103(3): 281-286.
[6] Torregrosa A, Ortí E, Martín B, et al. Mechanical harvesting of oranges and mandarins in Spain[J]. Biosystems Engineering, 2009, 104(1): 18-24.
[7] Whitney J D, Smerage G H, Block W A. Dynamic analysis of a trunk shaker-post system[J]. Transactions of the ASAE, 1990, 33(4): 1066-1070.
[8] Horvath E, Sitkei G. Damping properties of plum trees shaken at their trunks[J]. Transactions of the ASAE, 2005, 48(1): 19-25.
[9] Láng Z. A one degree of freedom damped fruit tree model[J]. Agricultural Engineering International Cigr Journal, 2008, 51(3): 823-829.
[10] Horvath E, Sitkei G. Energy consumption of selected tree shakers under different operational conditions[J]. Journal of Agricultural Engineering Research, 2001, 80(2): 191-199.
[11] Torregrosa A, Martin B, Garcia Brunton J, et al. Mechanical harvesting of processed peaches[J]. Applied Engineering in Agriculture, 2008, 24(6): 723-729.
[12] Castro-García S, Blanco-Roldán G L, Gil-Ribes J A. Vibrational and operational parameters in mechanical cone harvesting of stone pine (Pinus pinea L.)[J]. Biosystems Engineering, 2012, 112(4): 352-358.
[13] Castro-García S, Blanco-Roldán G L, Gil-Ribes J A, et al. Dynamic analysis of olive trees in intensive orchards under forced vibration[J]. Trees, 2008, 22(6): 795-802.
[14] Adrian P A, Fridley R B. Mechanical fruit tree shaking[J]. California Agriculture, 1958, 12: 3-15.
[15] Aristizábal I D, Oliveros C E, Alvarez F. Mechanical harvest of coffee applying circular and multidirectional vibrations.[J]. Transactions of the ASAE, 2003, 46(2): 205-210.
[16] Polat R, Guner M, Dursun E, et al. Mechanical harvesting of almond with an inertia type limb shaker[J]. Asian Journal of Plant Sciences, 2007, 6(3): 528-532.
[17] Du X, Chen D, Zhang Q, et al. Dynamic responses of sweet cherry trees under vibratory excitations[J]. Biosystems Engineering, 2012, 111(3): 305-314.
[18] Wu C, He L, Du X, et al. 3D reconstruction of Chinese hickory tree for dynamics analysis[J]. Biosystems Engineering, 2014, 119(1): 69-79.
[19] Du X Q, Wu C Y, He L Y, et al. Dynamic characteristics of dwarf Chinese hickory trees under impact excitations for mechanical fruit harvesting[J]. International Journal of Agricultural & Biological Engineering, 2015, 8(1):17-25.
[20] 杜小强,倪柯楠,潘珂,等. 可调振幅单向拽振式林果采收机构参数优化[J]. 农业工程学报,2014,30(16):25-32.
Du Xiaoqiang, Ni Ke’nan, Pan Ke, et al. Parameter optimization of stroke-adjustable and monodirectional pulling fruit harvester[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE) , 2014, 30(16): 25-32. (in Chinese with English abstract)
[21] 杜小强,倪柯楠,武传宇. 基于外旋轮线轨迹的果品振动采收机构研究[J]. 农业机械学报,2016,47(3):59-66.
Du Xiaoqiang, Ni Ke’nan, Wu Chuanyu. Vibratory harvesting mechanism for tree fruit based on epitrochoid[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3): 59-66. (in Chinese with English abstract).
[22] 杜小强,李党伟,贺磊盈,等. 基于电子果实技术的机械振动采收过程果实运动分析[J]. 农业工程学报,2017,33(17):58-64.
Du Xiaoqiang, Li Dangwei, He Leiying, et al. Fruit motion analysis in process of mechanical vibration harvesting based on electronic fruit technique[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(17): 58-64. (in Chinese with English abstract)
[23] 乔园园,牛长河,孟详金,等. 牵引式林果振动采收机的设计与田间试验[J]. 新疆农业科学,2015,52(3):528-534.
[24] 王长勤,许林云,周宏平,等. 偏心式林果振动采收机的研制与试验[J]. 农业工程学报,2012,28(16):10-16.
Wang Changqin, Xu Linyun, Zhou Hongping, et al. Development and experiment of eccentric-type vibratory harvester for forest-fruits[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(16): 10-16. (in Chinese with English abstract)
[25] 蔡菲,王春耀,王学农,等. 基于高速摄像技术的振动落果惯性力研究[J]. 西北农林科技大学学报:自然科学版,2013,41(4):208-212.
Cai Fei, Wang Chunyao, Wang Xuenong, et al. Inertia force of fruits abscised by vibration based on high-speed video camera technology[J]. Journal of Northwest A&F University: Nat. Sci. Ed, 2013, 41(4): 208-212. (in Chinese with English abstract)
[26] 付威,何荣,曲金丽,等. 自走式矮化密植红枣收获机的设计[J]. 农机化研究,2014,36(4):106-109.
[27] 范雷刚,王春耀,刘梦霞,等. 振动参数对果树采收影响的试验研究[J]. 农机化研究,2016,38(10):165-168.
[28] 杜小强,李松涛,贺磊盈,等. 三维激振果品采收机构优化设计与试验[J]. 农业工程学报,2017,33(16):48-55.
Du Xiaoqiang, Li Songtao, He Leiying, et al. Optimal design and experiment on vibratory fruit harvesting mechanism with three-dimensional excitation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(16): 48-55. (in Chinese with English abstract)
[29] 王冬,陈度,王书茂,等. 基于有限元方法的整形果树振动收获机理分析[J]. 农业工程学报,2017,33(增刊1):56-62.
Wang Dong, Chen Du, Wang Shumao, et al. Analysis on vibratory harvesting mechanism for trained fruit tree based on finite element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(Supp.1): 56-62. (in Chinese with English abstract)
[30] 散鋆龙,杨会民,王学农,等. 振动方式和频率对杏树振动采收响应的影响[J]. 农业工程学报,2018,34(8):10-17.
San Yunlong, Yang Huimin, Wang Xuenong, et al. Effects of vibration mode and frequency on vibration harvesting of apricot trees[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(8): 10-17. (in Chinese with English abstract)
[31] 散鋆龙,杨会民,王学农,等. 振动收获过程中杏果实脱落的动态响应分析[J]. 农业工程学报,2018,34(18):68-75.
San Yunlong,Yang Huimin,Wang Xuenong, et al. Dynamic response analysis of apricot fruit dropping during vibration harvesting[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(18): 68-75. (in Chinese with English abstract)
Influence of different vibration characteristic parameters on vibration response of apricot trees
Yang Huimin1, San Yunlong2, Chen Yifei1, Wang Xuenong1※, Niu Changhe1, Hou Shulin2
(1.830091,; 2.100083)
In this paper, the combination of finite element modeling and experiment was used to study the effects of different vibration parameters such as vibration time (), amplitude () of the vibration excitation point on apricot tree vibration and vibration frequency (), and optimize the performance of forest fruit vibration harvesting prototype. The effects of different vibration parameters on the vibration detection points of apricot trees were analyzed by vibration response test. The response analysis of apricot tree free modal vibration using ANSYS Workbench software showed that apricot trees had typical free modal responses at 15, 26, 30 and 40 orders, the corresponding frequencies were 5.5, 10.5, 15.1, and 29.3 Hz, respectively; and the maximum displacement deformation of fruit trees was 286.5, 261.9, 267.2, and 273.5 mm, respectively. The typical free modal cloud image analysis showed that the typical free modalities of the 15th and 26th orders were higher in the terminal end responsiveness of the apricot branches. The 30th order fruit tree had a high overall response consistency, and the apricot tree had the largest deformation response at the end; at the 40th order of 29.3 Hz, some branches of the fruit trees were severely deformed, and the overall structure of the tree was easily destroyed. The optimal response frequency of apricot tree vibration harvesting ranged from 0 to 20 Hz. The harmonic response analysis showed that in the optimal frequency range, the acceleration of the same position increased with the increase of the excitation amplitude at the same frequency, but the overall variation of the vibration curve was consistent with the trend; When the amplitude of the vibration excitation point of the apricot tree was 5, 10 and 15 mm, at the same frequency, as the excitation amplitude increased, the acceleration at the same position increased, but the overall variation of the vibration curve was consistent with the trend. The three-factor and three-level vibration response tests were conducted to study the effects of vibration time, vibration frequency and excitation point amplitude on the acceleration of three different detection points. The multivariate regression analysis of variance showed that the accelerations1and2of detection points 1 and 2 were less than 0.000 1, the overall model was highly significant (<0.01), and the model regression termsandwere significant. The acceleration3of the detection point 3 was 0.000 1, and the overall model was highly significant (<0.01), except that the acceleration3value of the detection point 3 of the model regression terms,and2was not significant (>0.05), and other regression terms were significant (<0.05). The factors which affected the acceleration of the detection points 1 and 2 were the same as the amplitude of the excitation point, vibration frequency and vibration time. The order of the magnitude of the acceleration affecting the detection point 3 was the vibration time, the amplitude of the excitation point, and the vibration frequency. Through the response equations of the three detection points, the coefficient of determination2of the regression equations from the bottom to the top three detection points were 0.906 7, 0.879 3 and 0.973 3, respectively. Using the Design-Expert 10.0.3 software to optimize the detection point response equation, the optimal vibration recovery parameter combination was that the vibration time was 7.207 s, the vibration frequency was 15 Hz, and the amplitude of the excitation point was 10 mm. The verification test showed that the acceleration from the bottom to the top of each detection point was 10.4, 10.2 and 9.3, which was similar to the optimized value. These conclusions can provide design and theoretical basis for the design of mechanical parameters of apricot vibration harvesting.
vibrations; harvesting; mechanization; apricot; vibration response test
10.11975/j.issn.1002-6819.2019.02.002
S225.93
A
1002-6819(2019)-02-0010-07
2018-09-10
2019-01-09
国家自然科学基金项目—新疆杏振动脱落动力学特性及振动采收机理研究(51465059)
杨会民,助理研究员,主要从事农业工程研究。Email:yhm_shz@163.com
王学农,研究员,主要从事农业工程与装备研究。Email:xjwxn2010@ sina.com
杨会民,散鋆龙,陈毅飞,王学农,牛长河,侯书林. 不同振动特性参数对杏树振动响应的影响[J]. 农业工程学报,2019,35(2):10-16. doi:10.11975/j.issn.1002-6819.2019.02.002 http://www.tcsae.org
Yang Huimin, San Yunlong, Chen Yifei, Wang Xuenong, Niu Changhe, Hou Shulin. Influence of different vibration characteristic parameters on vibration response of apricot trees[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(2): 10-16. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2019.02.002 http://www.tcsae.org
