基于双目视觉技术的供补弹机构对接方法
2019-02-25蒋丙栋王茂森戴劲松
蒋丙栋,王茂森,戴劲松
(南京理工大学 机械工程学院, 南京 210094)
传统的补弹车弹链与火炮弹箱对接借助于人工操作,过程繁琐,效率低下,操作人员的劳动强度大。并联结构具有刚度高、速度快、柔性强、重量轻等优点[1],在空间对接,汽车装配线上的车轮安装,医院中的假肢接骨等场合得到了广泛的应用[2],已成为机器人研究的热点之一。将并联结构应用于对接过程的位姿调整可以降低操作人员的劳动强度,提高效率。精确检测并联机器人的末端位姿对实现并联机器人的高性能控制具有重要意义[3]。立体视觉具有非接触,快速检测,高智能化等优点,能够高效、灵活地完成多自由度测量,克服并联机构位姿检测在传统检测方法中的不足[4]。本文将并联机构应用于供弹链与火炮弹箱对接过程的末端位姿调整,将立体视觉技术应用于弹链末端与弹箱的相对位姿测量,通过追踪标志点,利用数值方法对机构位姿进行求解,实现了对接过程中的位姿解算。
1 自动对接系统
对接系统装置结构简图如图1所示,主要由弹箱,柔性弹链,3-RPS并联机构,测量装置(未画出)组成;测量装置包括与定平台固连的相机,及与弹箱固连的识别点。3-RPS并联结构由与柔性弹链固连的动平台,与底座固连的定平台,和三条支链组成;每条支链由三个运动副组成,由定平台至动平台依次为转动副,移动副,球副;3-RPS具有三个自由度,即垂直方向的移动和两个水平轴的的转动自由度[5]。
左右相机(未画出)获取距离角度参数,执行机构驱动对接机构运动完成对接动作。该方法能够有效提高对接效率,降低对接过程操作人员的劳动强度,提升装备技术水平。

图1 对接系统装置结构简图
2 双目测量系统
2.1 双目测量原理
双目立体测量技术基于视差原理,利用空间的特征点在两个相机成像平面上的坐标求解空间特征点的三维坐标[6-7]。
如图2所示为双目立体视觉测距原理几何模型图。P为空间任意一点,在左右相机成像平面的点分别为Pl,Pr,立体视觉的测距主要是根据三角测距原理,在找出几何模型中的一对相似三角形,由标定过后得到的参数数据,即可求得距离深度。对应关系式:
(1)
式中:Z为目标点距离,T为基线距离,xl、xr分别为左右图像坐标系内像素点的横坐标,d为视差,f为焦距。
对于一个匹配的特征点,它在相机坐标系(以左相机投影中心为原点)中的坐标是可知的,因此可以对该坐标点进行重投影到世界坐标系中,得到该特征点的三维坐标。投影关系可表示为:
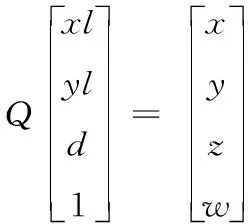
(2)
其中:Q是重投影矩阵,表示为:
(3)
为了计算统一而引入了第四维度w,使三维坐标(x,y,z)用齐次坐标表示时变为四维空间(x,y,z,w),因此求得物点P的三维坐标为(x/w,y/w,z/w)。
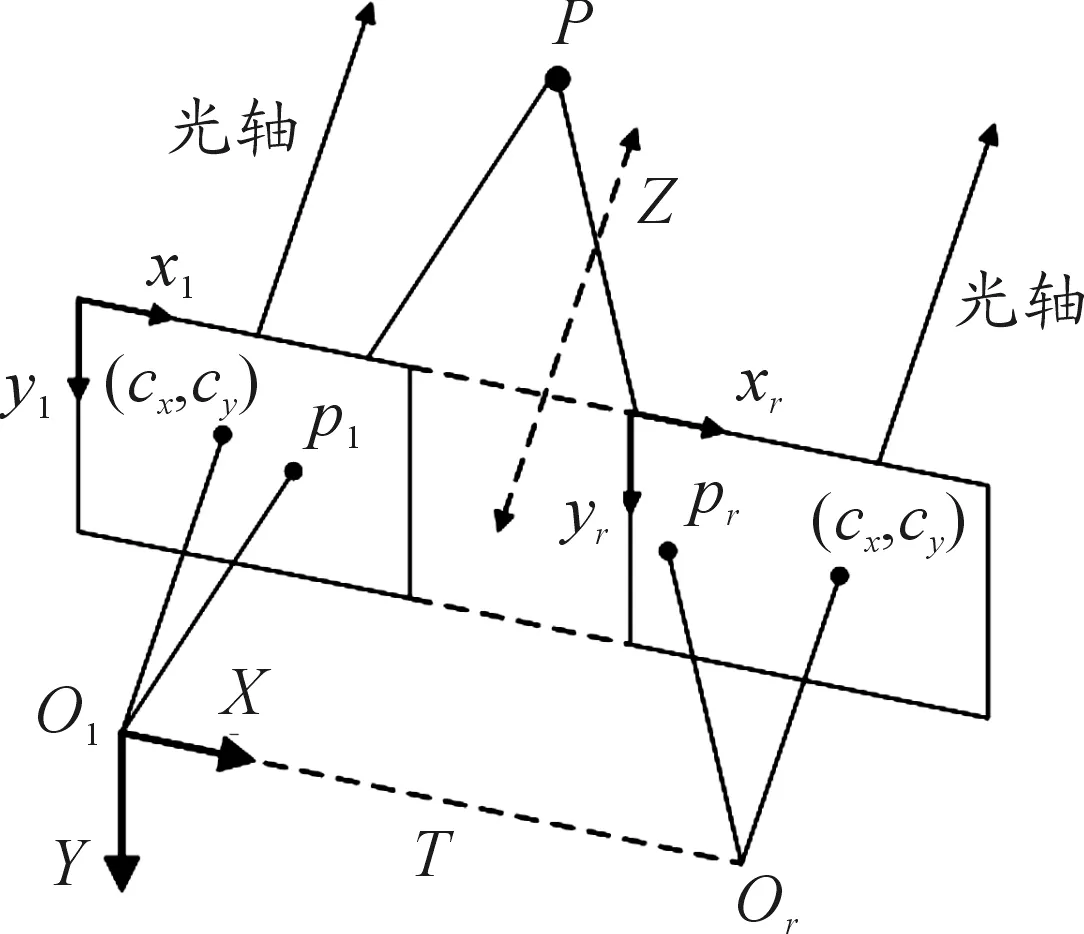
图2 双目立体测距原理几何模型图
2.2 对接特征点
因对接卡口结构较为复杂,特征点与特征曲线的选取较难,本文采用设置标志点的方式将目标的识别进行简化,常用的标志点有:扇形编码标志点,彩色编码,圆形标号[8];本文选用圆形标号标志点(图3),一个大圆内有标有O,X,Y三个字母,以标志点O的圆心为原点建立直角坐标系,X轴过X标志点中心,Y轴过Y标志点中心,Z轴垂直XY平面向内,将三个标志点置于与弹箱位置关系固定的平台上,其位置关系如图4所示;
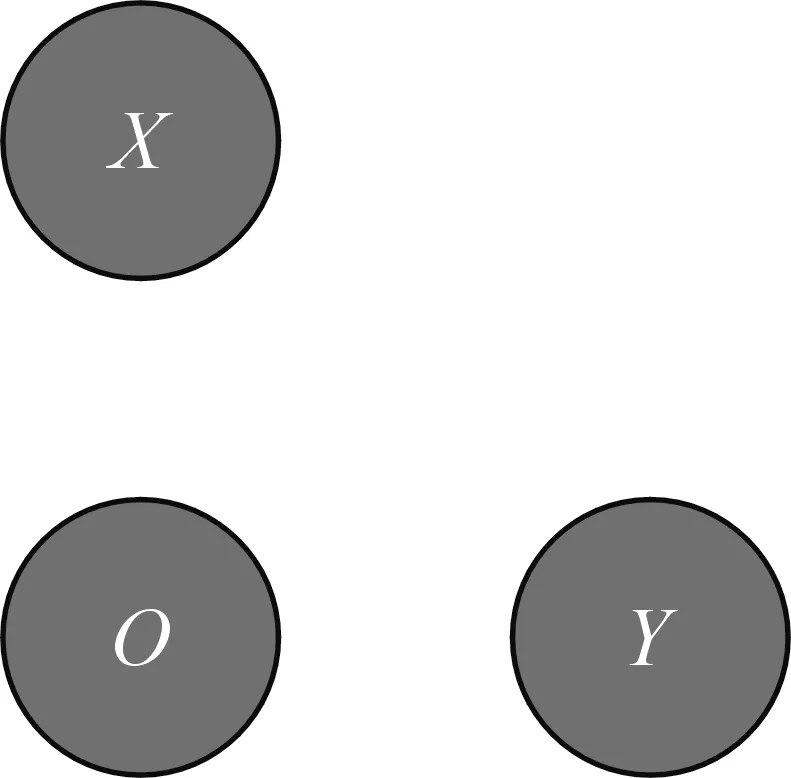
图3 标志点

图4 火炮弹箱对接口与标志点平面示意简图
3 位姿解算
3.1 标志点位姿解算
将标志点坐标系定义为{S},设O,X,Y标志点在相机坐标系中的坐标分别为,PO=(XO,YO,ZO)T,PX=(XX,YX,ZX)T,PY=(XY,YY,ZY)T,则:
(4)
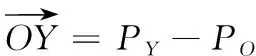
(5)
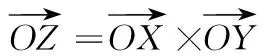
(6)
将其单位化为SX,SY,SZ;
相机坐标系至标志点坐标系的变换矩阵为:
(7)
其中:
(8)
3.2 并联机构位姿解算
3-RPS并联机构简化为如图5,A1A2A3为定平台,B1B2B3为动平台,分别在定平台和动平台上建立坐标系OA-XAYAZA和OB-XBYBZB。对并联机构的位姿分析任务是找到动平台的位姿与输入杆的长度之间的关系,3-RPS并联机构末端位姿为坐标系OB-XBYBZB的位姿[9]。

图5 3-PRS并联机构示意图
目前对并联机构的运动学求解多采用欧拉角,四元数进行推导[10],本文根据3-RPS并联机构的特点,对其进行几何分析,采用欧拉角求解运动学逆解。定平台的三个铰点Ai在坐标系OA-XAYAZA上的坐标表示为:
(9)
Bi在OB-XBYBZB中的坐标为:
(10)
取Z-Y-X型欧拉角(γ,β,α),则动平台相对定平台的方向余弦为:
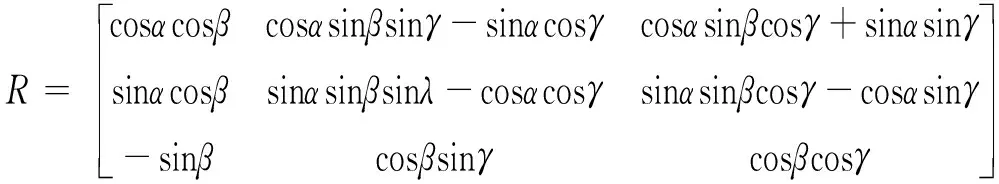
(11)
动平台上的三个球铰在固定坐标系A中的坐标为:
OBA=R·B+P
(12)
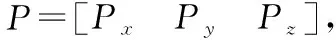
由此可求得杆长为:
Li=OBAi-Ai=R·Bi+P-Ai,i=1,2,3
(13)
从而求得并联机构的位置反解。
3.3 相对位姿求解
要驱动弹链对接口与火炮弹箱对接口完成对接,只需获得火炮弹箱对接口相对于定平台的位姿,即可驱动动平台运动到指定位置,从而完成对接动作。
以定平台坐标系{A}为世界坐标系,火炮弹箱对接口坐标系记为{H},弹链对接口坐标系记为{D},左相机坐标系记为{C},标志点确定的坐标系为{S},动平台坐标系{B}相对于定平台坐标系{A}的位姿可表示为:
BTA=BTH⊕HTS⊕STC⊕CTA
(14)
其中BTH代表火炮弹箱对接口坐标系{H}到动平台坐标系{B}的变换矩阵,若顺利完成对接,弹链对接口坐标系{D}与火炮弹箱对接口坐标系{H}重合,则BTH=BTD,而动平台相对弹链接口只有平移;HTS为标志点坐标系{S}到火炮弹箱对接口坐标系{H}的变换矩阵,只有平移变换;STC为标志点坐标系{S}相对相机坐标系{C}的变换矩阵,由相机测量标志点位置获得;CTA为定平台坐标系{A}到相机坐标系{C}的变换矩阵,只有平移变换。
由BTA可求得Z-Y-X型欧拉角(γ,β,α),即可由式(13)求得杆长Li。
4 精度试验
1) 测距试验
本实验在墙壁上设置一个圆球,双目相机安装在一个装有直线导轨的三脚架上面,通过前后移动三脚架对网球的距离进行计算,将测量值与实际值进行了比较,有关数据如表1。
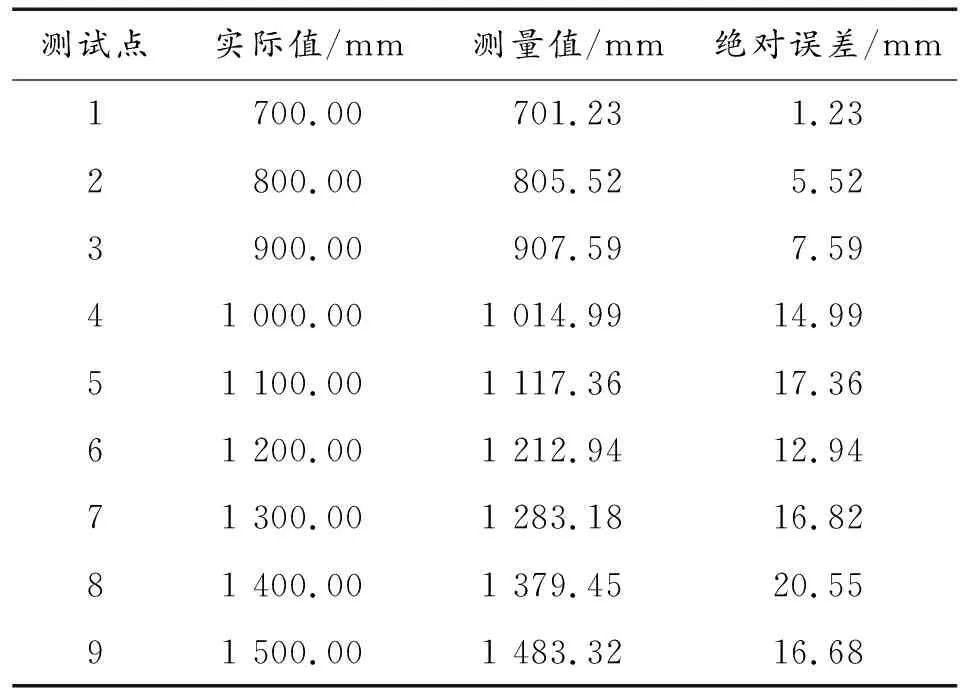
表1 测距实验数据
弹链与弹箱通过卡扣卡紧,对接时要求弹链与弹箱间距离测量的绝对误差小于20 mm。测试数据表明,测量的绝对误差在允许范围内,该测量系统能满足距离测量的要求。
2) 定位试验
使用AutoCAD制作一张如图6所示的测试纸,其中9个圆点的直径为8 mm,相邻点的间距随机不等。在测试时使用双目立体相机对图中1~9个典型目标点进行识别,计算出各点在XOY坐标平面内的坐标(x,y),此时的计算结果是图中各点在双目立体相机坐标系(以左相机为坐标原点)下的坐标值,既绝对坐标。但是,绝对坐标的正确性与准确性较难检验。因此,本文采用相对坐标的方式进行间接测试,即选点1为坐标原点,计算其余各点相对于该点的坐标值(X,Y)。通过计算相对坐标的实际值与测量值之间的误差,判断双目立体视觉定位的精度。实测数据列于表2和表3。试验表明,双目视觉模块具有良好的定位精度。
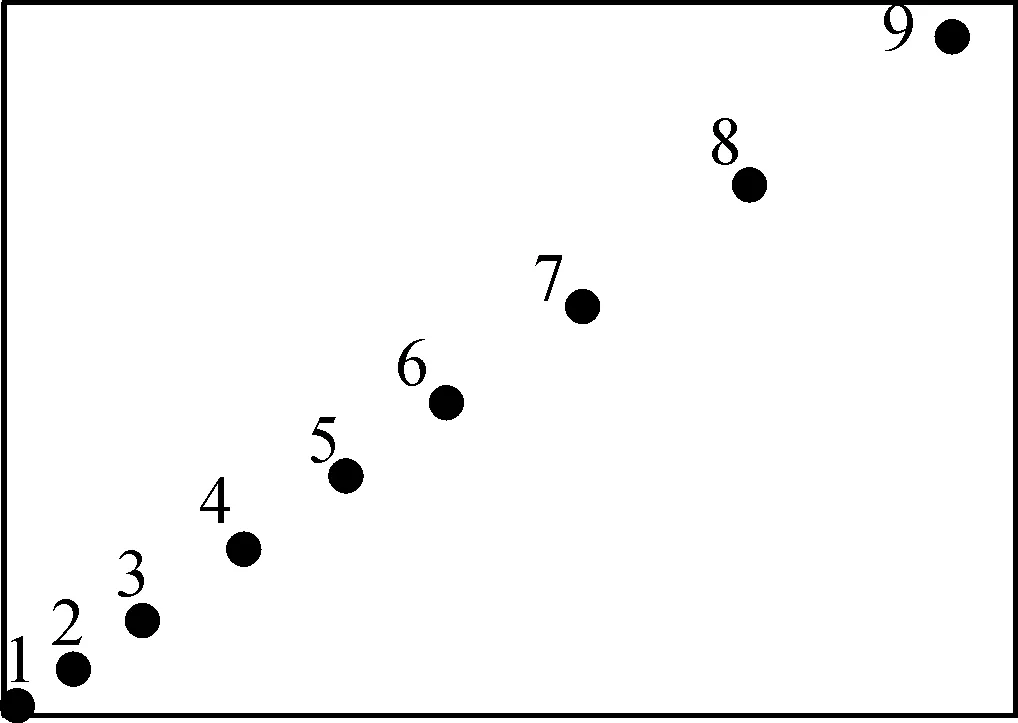
图6 定位试验用测试图
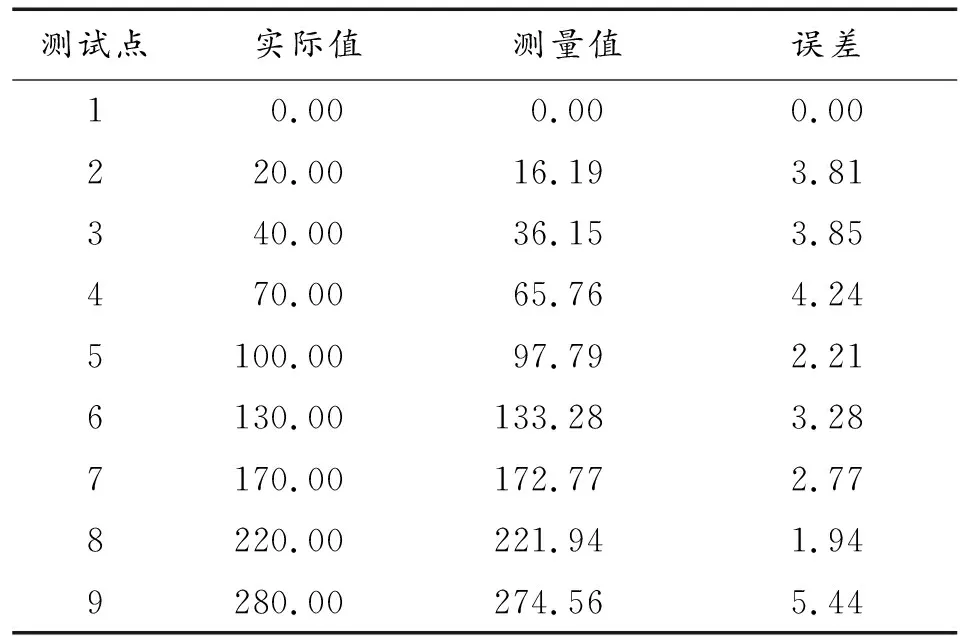
mm
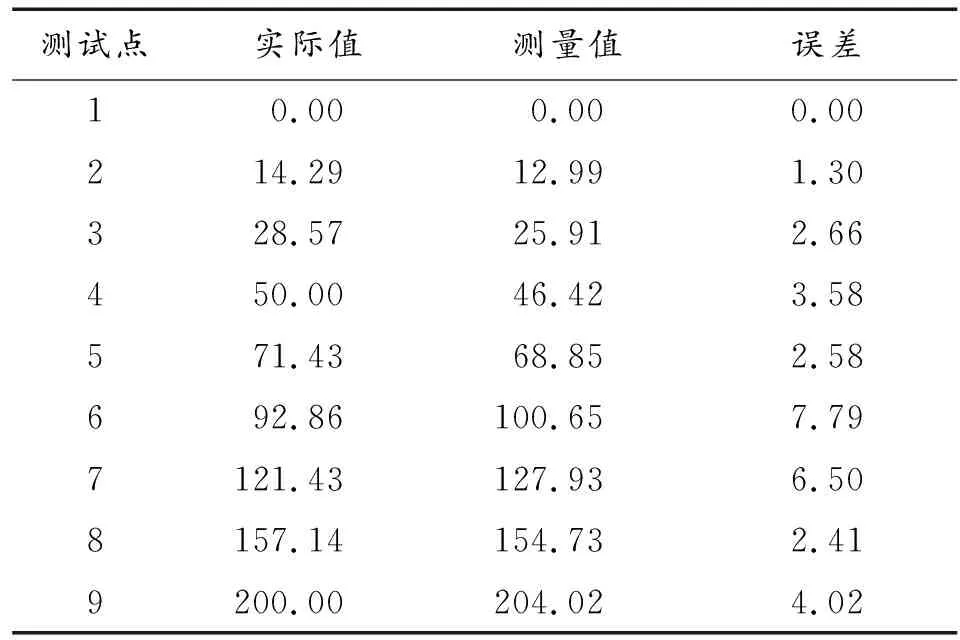
表3 Y方向定位实验数据 mm
5 结论
1) 将立体视觉技术应用于位姿的测量,将并联结构应用于末端的位姿调整,根据立体视觉的测量结果,对弹箱与弹链的相对位姿进行了解算,求解出并联机构的位置反解,对立体视觉的测量精度的试验表明测量精度满足对接需求。
2) 理论和试验结果表明,本文的方法可满足补弹车输弹链与火炮弹箱的自动化对接要求,可为立体视觉技术与机器人结合的实际应用提供参考。
