主动防护发射转台静态与模态特性分析

陆 谦，陈 曦，许国杰，杜忠华，隋红霞

(1.南京理工大学 机械工程学院， 南京 210094； 2.黑龙江北方工具有限公司， 黑龙江 牡丹江 157000)

主动防护系统的发展水平是一个国家国防实力的重要标志，近年来逐渐成为各军事大国普遍关注的高精尖技术之一，作为主动防护系统的一个关键功能部件，主动防护发射转台的性能直接决定着主动防护系统的防护效能，是主动防护系统向高效、精准、智能方向发展的最佳选择之一。主动防护系统的发展对主动防护发射转台的性能提出了更高、更新的要求。因此，进行主动防护发射转台的相关性能研究对于国防事业的建设具有重要的意义。

目前，主动防护发射转台的研究方向主要包括机械结构研究和控制系统研究，在机械结构研究方面，相关工作主要致力于提高主动防护发射转台的转动精度、稳定性和承载能力。由于主动防护发射转台特殊的应用场景，分析其在相关载荷作用下的最大承载力是保证武器系统实现预定精度指标和性能的关键环节，将直接影响武器系统的动态精度和控制系统的可靠性[1]。耿雷等[2]使用 Pro/E对结构进行了建模与运动仿真，并使用ANSYS进行了静力计算和模态分析。马伯渊等[3]考虑风载和偏心载荷，对车载雷达转台刚度和强度进行了分析。董军等[3]对某型导弹发射转台的整体结构进行了数值仿真，并对其中变形较大的部位进行了局部改进。张俊晶等[4]对双轴转台装配体进行模态分析，并对薄弱构件进行结构改进，最终达到预期效果。还有很多人做了类似的工作，但是他们研究的转台工作环境并不需要承受较大的静载荷和动载荷，且不需要考虑主动防护发射系统的发射冲击频率[5]。主动防护发射转台由于其应用场景的特殊性，很少有关于此类结构的有限元分析，可借鉴的设计经验和参考很少，因此，针对主动防护发射转台进行有限元仿真分析，利于发现设计中存在的问题，为主动防护系统的机械结构设计提供依据。

1 物理模型的建立

1.1 主动防护发射转台结构及有限元模型的建立

本文研究的主动防护发射转台为双轴立式转台，主要由轴承、同步带轮、交流伺服电机、驱动器、编码器、蜗轮蜗杆减速器等部件组成。由于主动防护发射转台工作环境的特殊性，要求驱动电机具有精确的位置控制和速度控制特性，因此选择交流伺服电机作为主动防护发射转台的2个驱动电机，并通过蜗轮蜗杆减速器和同步带传动来实现转台的力矩传动。由于旋转主轴主要承受径向力，承受的轴向力很小，选用圆锥滚子轴承作为旋转主轴的回转轴承。根据其设计方案首先在Solidworks中建立主动防护发射转台的简化三维模型，其三维结构示意图如图1所示。

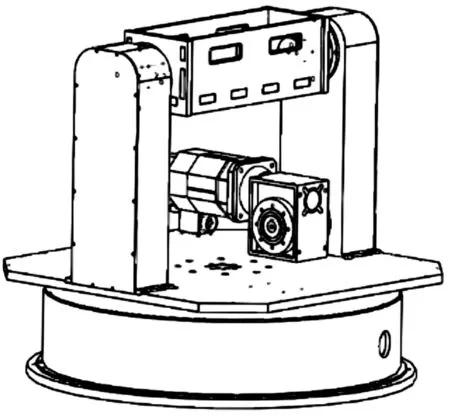
图1 主动防护发射转台三维结构示意图

对主动防护发射转台的研究需要多种学科的有机结合，要精确完整的建立其动静力学模型相当复杂。因此，为了提升系统计算的运行速度，需将Solidworks中建立的三维模型简化。对于电机、驱动器、减速器、带轮、防尘壳等部件，可以忽略其具体结构， 仅计算其施加于相应的安装位置的重力。同时忽略螺栓及部分螺纹孔，将零部件上的一些细节修饰特征进行压缩处理，如倒角、圆角、键槽和定位孔等[6-7]。

根据主动防护发射转台结构中各零件所用材料类型，在ANSYS Workbench中设置各主要零部件的材料属性，如表1所示。

表1 主动防护发射转台主要零部件材料属性

在对主动防护发射转台的单元划分时，考虑到主动防护发射转台是由多种材料、多种形状的构件组成的装配体，因此采用自动划分的网格划分方式，使用实体单元Solid 187四面体单元。同时轴承等具有相对运动功能的部件，受力情况复杂，其内外圈的边界条件和滚子受力情况都难以准确确定，为了尽可能的满足对其刚度和自由度的准确模拟，此处对其进行等效简化处理。网格划分后的主动防护发射转台有限元模型如图2所示。整个转台总共被划分成 338 748个单元，820 799个节点。

1.2 接触与约束等边界条件的施加

主动防护发射转台各零部件间通过各种连接关系连接在一起，包括有定位关系、轴承连接关系、螺栓连接关系和焊接关系等，其有限元模型如图2所示。螺栓连接关系与焊接关系的零部件之间不存在相对运动，可用绑定接触Bonded模拟，如耳轴与上底板、发射箱的各安装板间的接触等。用润滑油润滑的零部件之间的连接和定位关系可以近似视为无摩擦滑动，可用无摩擦接触Frictionless模拟，如轴承座与轴承端面的接触等。由于系统工作时底部轴承座和机架固连，因此对底部轴承座的底平面施加固定约束Fix support。

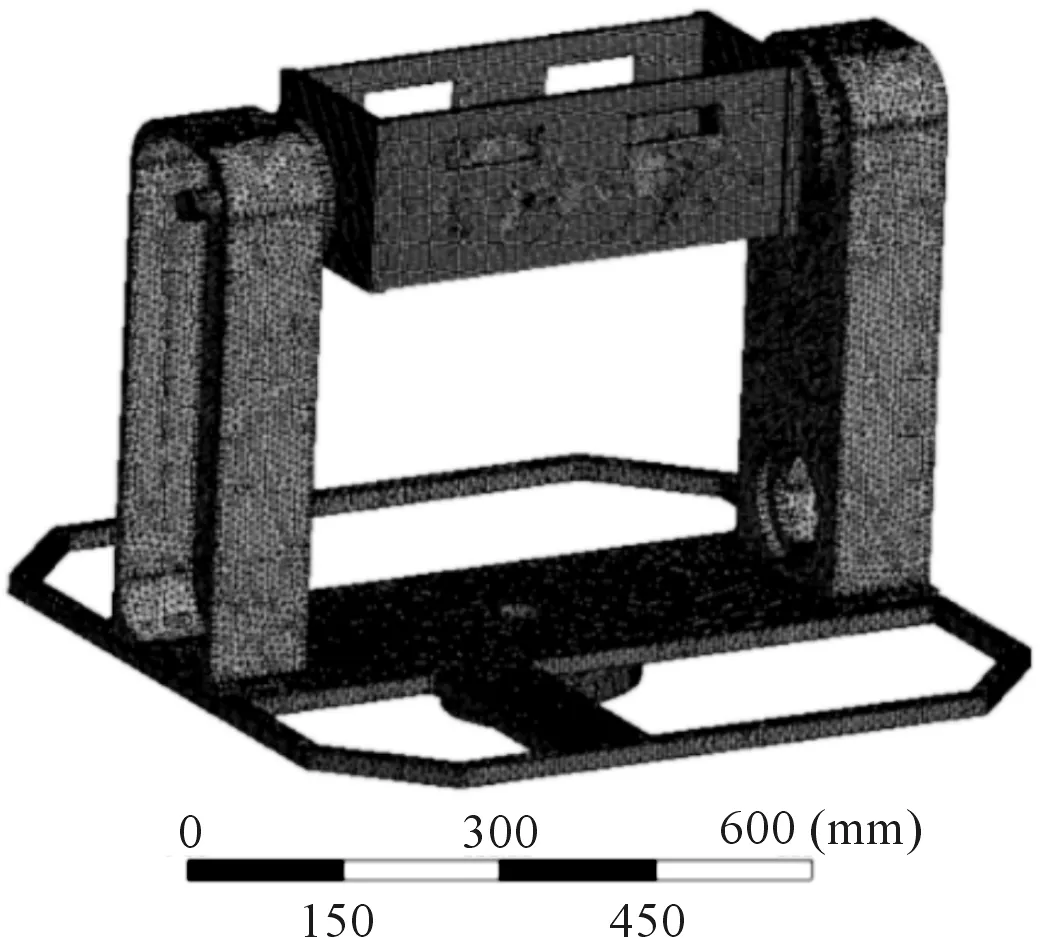
图2 主动防护发射转台有限元模型

主动防护发射转台的静态分析主要是机构在重力作用下的变形分析，而电机、发射模块等其他设备难以真实模拟，因此将其重量以施加载荷的形式加载于主动防护发射转台上，当发射箱口部处于开口向上的状态时，防护单元的重力可等效为400 N垂直于发射底板向下的压力，底板受电机、减速器及驱动器的重力等效为580 N垂直于底板向下的压力，带轮及皮带的重力等效为40 N作用于轴圆柱面外表面竖直向下的压力，在Inertial中对整体结构施加整体重力加速度Standard Earth Gravity为9.8 m/s2。

2 求解与结果分析

2.1 静力学分析

由于发射系统必须装在主动防护发射转台上，其静压变形会对发射起点位置产生影响，进而影响发射精确度，因此需对主动防护发射转台进行静力学分析，防止静压变形对主动防护系统的发射精度产生较大影响。

主动防护发射转台的静力学分析属于弹性力学分析，进行弹性力学分析时，需作出如下假设条件：连续性假设，材料是均匀分布的；均匀性假设，材料是均匀分布的；各向同性假设；线弹性假设；小变形假设。其动力学通用方程为

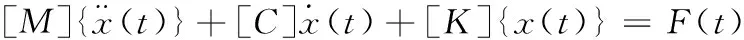
(1)

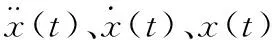
在线性静力结构分析中，所有物理量均不随时间变化，于是便得到线性静力方程：

[K]{x(t)}=F(t)

(2)

式(2)中，[K]为刚度矩阵，x(t)为位移矢量；F为静力载荷。

通过对式(2)的求解，可得所有节点的位移矢量{u}。弹性力学对节点的应力应变表达式为：

{εθi}=[B]{u}-{εth}

(3)

{σ}=[D]{εθi}

(4)

其中，{εθi}为应变； {εth}为热应变矢量，主动防护发射转台的静力学分析不考虑热应变；[B]为节点的应变；{σ}为应力的矢量；[D]为弹性矩阵[8]。

通过对式(3)及式(4)两式的求解，求解出节点的应力应变，并利用有限元理论将网格单元的应力应变求解得到主动防护发射转台整体应力应变结果。

图3为主动防护发射转台的应力云图。可以看到其最大应力区域主要集中在底板上，且主要体现在底板与底部回转支撑轴承固定的外圈位置和底板与耳轴接触的边沿位置，其中装载电机的一侧应力最大为σmax=33.471 MPa。而40Cr的许用抗压弯应力为σb=365.7 MPa，根据使用情况，取安全系数n= 2.5，则[σ]=σb/n=146.28 MPa，σmax≤[σ]，这说明主动防护发射转台的结构设计及材料选择满足强度要求且有较大余量。

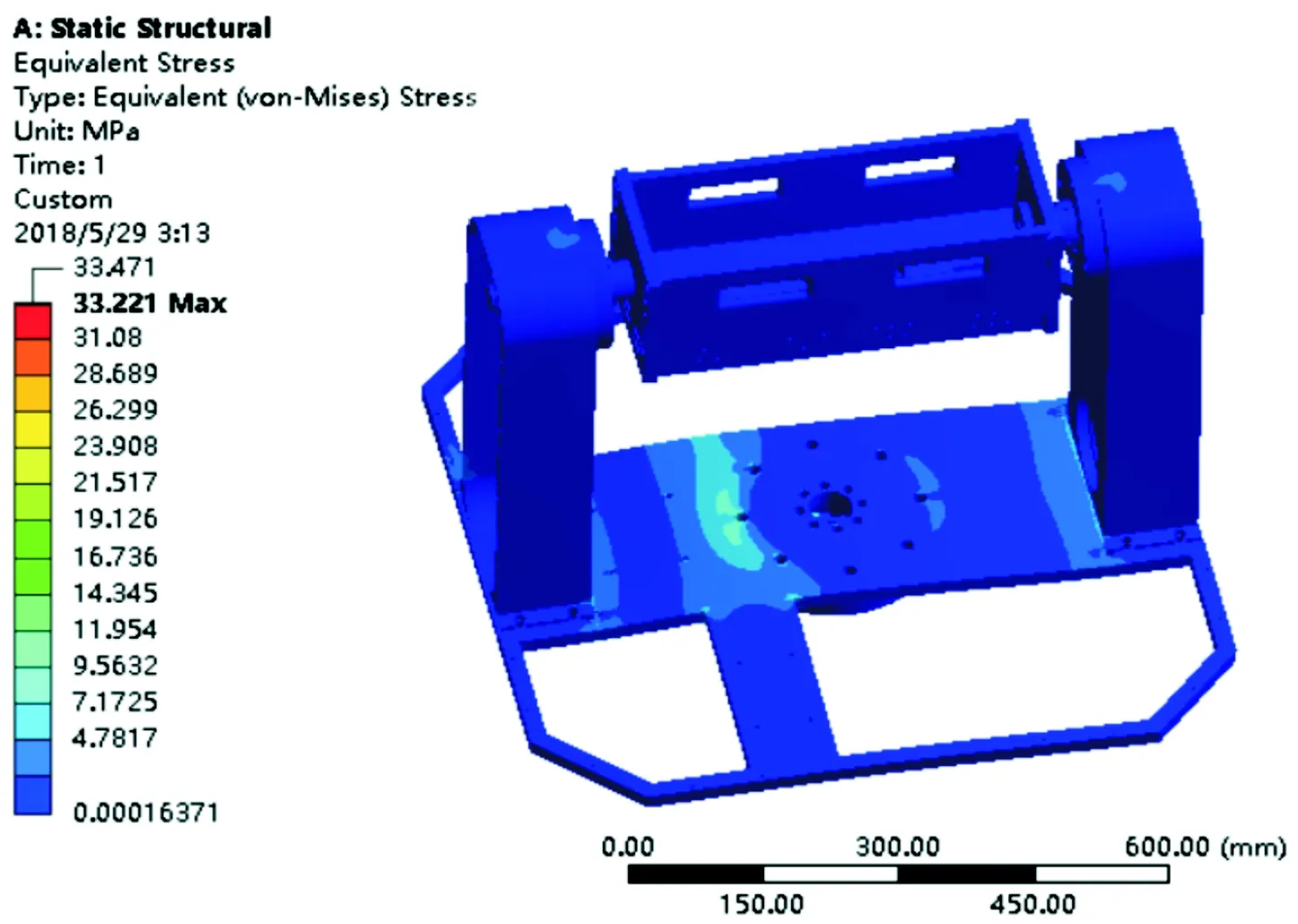
图3 主动防护发射转台的应力云图

主动防护发射转台在静载荷下的位移变形云图如图4所示。由图4可知，最大位移出现在主动防护发射转台的底板位置，可达到 0.104 34 mm。主动防护发射转台各零件的位移主要是由于底板变形导致的，底板导致的各零件位移使主动防护系统在该发射姿态下的起点位置发生改变，影响主动防护发射的精确度。因此可以考虑在今后的设计中加强底板的强度，如增加底板厚度或加装肋板。由于主动防护发射转台在该姿态下受静压载荷变形不大，在X、Y、Z方向的位移变形值分别为 0.060 851 mm，0.004 618 6 mm，0.005 933 2 mm，如果考虑修改设计方案，可能会增大主动防护发射转台的结构尺寸和重量，增大结构的转动惯量和电机的负载，进而增加设计成本。因此此处可考虑根据变形值，通过电路控制主动防护发射转台的位置补偿，抵消掉发射的起点位置变化，增加其位置精度，提高主动防护系统的防护性能。

2.2 模态分析

模态是机械结构固有的振荡特性，模态分析是进一步振动分析的基础，机械系统的每一阶模态具有其特定的固有频率和模态振型。为了避免产生共振，主动防护发射转台的固有频率必须高于主动防护系统的工作频率，将自身固有频率与外界激励频率间的耦合降到最小，有利于提高其刚度，减小工作负荷，提高发射精度，延长其使用寿命。

对主动防护发射转台进行模态分析需作出如下假设：所有材料均为线弹性材料，且材料特性不变；整体刚度不变、整体质量不变；求解使用小挠度理论进行，忽略材料的非线性特性，默认为线性分析求解。

主动防护发射转台的模态分析是在通用动力学方程的基础上删除载荷项及阻尼项，求解方程为

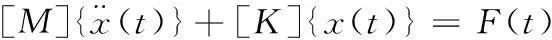
(5)

{x(t)}={∅icoscos(ωit)}

(6)

将式(6)代入式(5)中，得到最终求解的基本方程：

[K]{∅i}=ω2[M]{∅i}

(7)

式(7)中，ωi为第i阶固有频率，{∅i}为第i阶固有频率振型[9]。

理论上主动防护发射转台有无限多个固有频率，且固有频率值随模态阶数的增加而增加，其中数值最小的为1阶频率，但在结构振动中，高阶模态能量占比太低，对整个结构震动影响不大[10-12]，且转台上激振力的频率一般都不太高，因而激振频率只会和低阶模态的固有频率重合或接近。本文对前6阶模态进行了分析，其1～6阶振型图如图5。可以观察在1阶模态下的最大变形位置主要集中于耳轴的顶部位置和发射箱的底部位置，在2阶模态下的最大变形位置主要集中于发射箱中部的顶部位置，在3阶模态下的最大变形位置主要集中于耳轴的顶部外侧边缘位置，在4阶模态下的最大变形位置主要集中于发射箱中部的顶部位置，在5阶模态下的最大变形位置主要集中于耳轴的顶部外侧边缘位置和发射箱中部的顶部位置，在6阶模态下的最大变形位置主要出集中于发射箱顶部边缘位置。

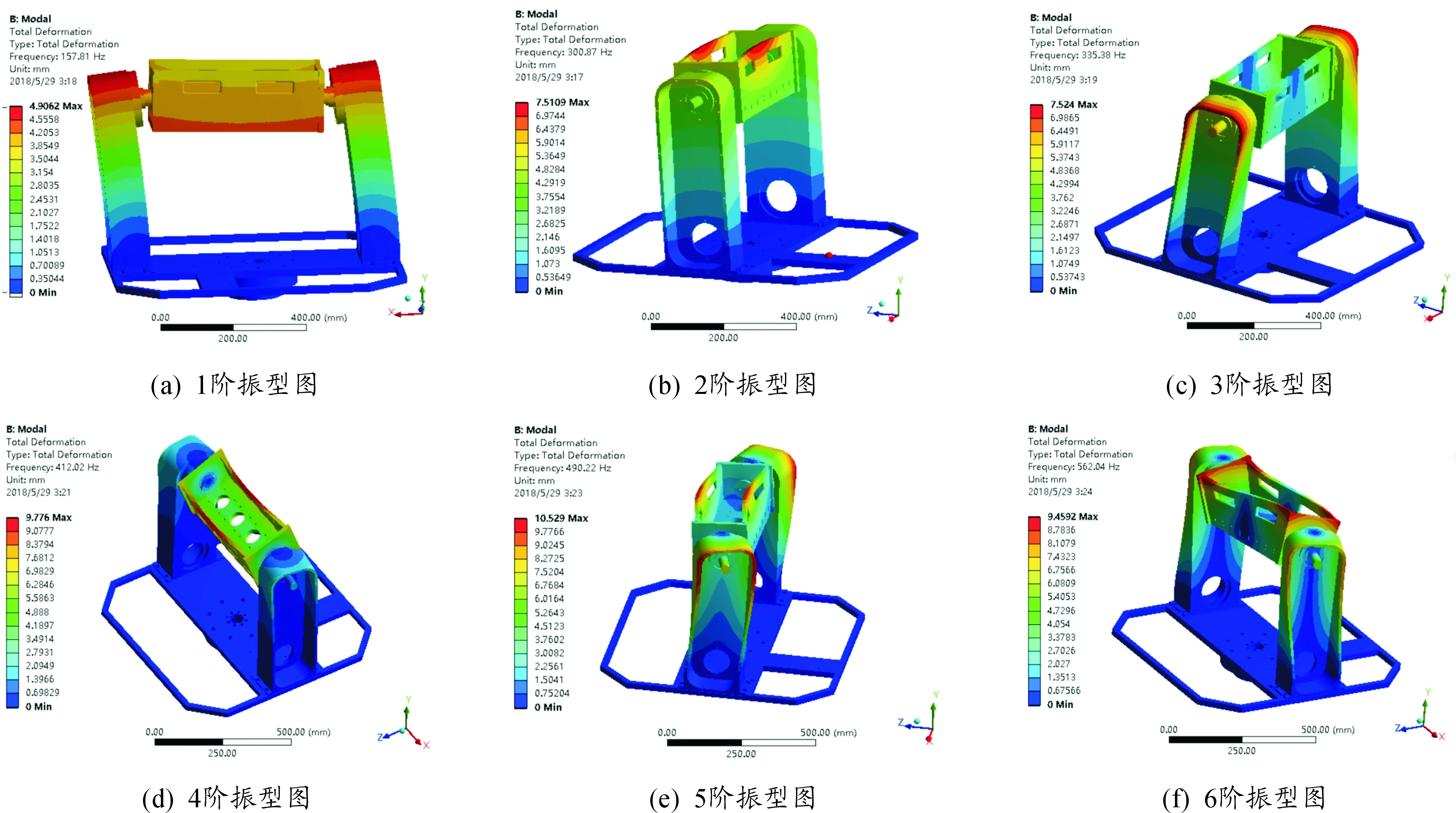
图5 主动防护发射转台前6阶振型图

主动防护发射转台的前6阶固有频率、振型及最大变形量，如表2所示。可以观察到在前6阶模态中模态阶数越高，固有频率越大，且在1阶模态中固有频率最小为157.81 Hz，6阶模态中固有频率最大为562.04 Hz；在1阶与2阶模态间模态固有频率和最大变形量增幅最大，分别为为143.06 Hz和2.604 7 mm；在1阶模态中的变形量最小为4.906 2 mm， 5阶模态中的变形量最大，最大变形量可达10.529 mm。

主动防护系统的外界激励频率主要来源于发射系统的射速和电机的转动振动。当仅考虑电机振动频率时，电机经过减速器(减速比为1∶30)减速后的转速为150 r/min，则电机转速为4 500 r/min，根据转速与频率之间的关系式:

n=60f

(8)

式(8)中：n为电机转速；f为电机振动频率[11]。求得电机在最大转速 4 500 r/min下的激振频率为75 Hz，远低于主动防护发射转台的1 阶频率。这说明电机与主动防护发射转台不会发生共振。

而在仅考虑发射系统的射速时，在发射系统的射速为 5 000发/min下，其发射冲击频率为83.3 Hz，远低于主动防护发射转台的第1阶频率。因此发射系统与主动防护发射转台不会发生共振。

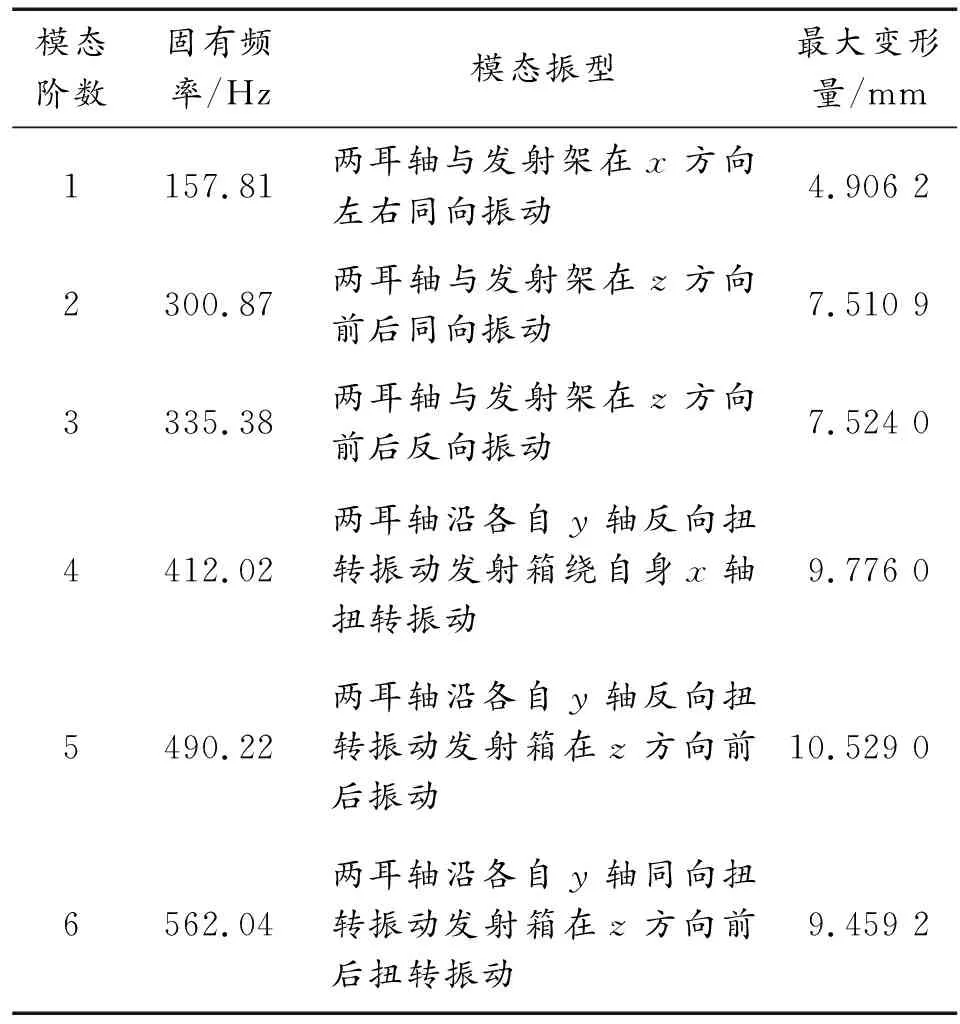
表2 主动防护发射转台前6阶固有频率、振型及最大变形量

3 结论

使用ANSYS Workbench对主动防护发射转台进行了研究，简化了主动防护发射转台的模型，并通过施加载荷的方法模拟等效主动防护发射转台上的机构负载和受力状况，得到静载情况下机构的应力和变形云图及固有频率和相应的主振型；确认了底板是双轴转台整体结构中刚度最薄弱的环节，并计算出了静载和不同模态下主动防护发射转台在各坐标系方向上的变形量，相比于依靠工程经验和粗略校核计算，可以更准确的模拟实际结构情况，提高计算效率。验证了主动防护发射转台结构的可行性，从而为今后有效、针对性的优化提供指导。