复杂约束条件下高超声速飞行器再入轨迹优化

张合新，宫梓丰，蔡光斌，宋 睿

(1.火箭军工程大学 导弹工程学院，西安 710025； 2.青州士官学院， 山东 青州 262500)

近年来，有关复杂约束的高超声速滑翔飞行器轨迹优化已经成了国内外研究的热点[1]。高超声速飞行器实际再入的过程中，不仅要考虑大气压强、热流量、热流密度等约束限制[2]，还要对再入环境状态(自然条件和政治军事因素)进行避障与突防[3-4]。现有的制导控制方法可以解决再入过程中的问题，而对于高超声速飞行器而言，要实现战略突防[5]。现今研究对禁飞区与突防的研究成果相对较浅[6]，是轨迹优化领域值得深入研究的课题。轨迹优化问题具有较高的非线性和复杂度，常规的变分法和极大值原理难以在规定时间内高效求解出最优解[7]，因而通常用数值法进行求解。伪谱法[8]是数值法的典型代表方法，大多数配点基于高斯积分规则[9]，采用契比雪夫或勒让德多项式，而后对全局进行插值[10]。文献[11]通过构建高超声速飞行器物理模型，考虑飞行任务中的过程约束和终端约束，利用伪谱法解决了轨迹优化问题；文献[12]进一步讨论了伪谱法再入轨迹制导的应用，但针对禁飞区约束条件没有作出细化考虑。针对改进自适应伪谱法，对最优控制问题进行转化，即将整个区间进行网格细化[13]，避免出现极其精细的网格化和不合理的高逼近多项式，并综合网格密度和插值多项式的阶次，使系统满足较快的收敛速度，提出最大轨迹空间概念，轨迹能够完整绕开禁飞区，且提升了原有精度。通过仿真计算结果计算状态量，评估轨迹状态性能得出结论。

1 再入模型构建

复杂约束下的高超声速滑翔飞行器再入轨迹优化与飞行器物理结构、过程及终端约束和目标方程息息相关，下面就对模型及约束分别进行定义。

1.1 滑翔飞行器再入运动学模型

高超声速滑翔飞行器再入过程受到很多约束的限制，信号通道间的耦合问题也较为突出，且非线性特征明显，其动态变化可由一组非线性微分方程表示[9]。假定地球为均匀光滑的球体，则滑翔飞行器再入过程中的位置变化如下：

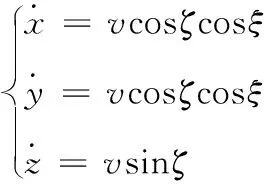
(1)

式(1)中，x、y、z分别是飞行器在航迹坐标系下三个轴所对应的位移分量；v是飞行器的线速度；ζ为航迹倾角；ξ为航迹方位角。飞行器的速度、航迹方位角和航迹倾角的一阶微分满足以下关系：

(2)

式(2)中，Q、S、g、m和σ分别代表飞行器的动压、再入参考面面积、重力加速度、飞行器质量和倾斜角(bank angle)；KD、KL、KY分别是飞行器的阻力系数、升力系数和侧向力系数。动压Q满足公式：

(3)

式(3)中，ρ表示大气密度。其大小会随飞行高度的变化而发生改变，一般用如下的公式进行拟合：

(4)

式(4)中:ρ0为海平面标准大气密度；re为地球半径；H为常值。

1.2 约束条件

为进一步模拟实际飞行条件，在轨迹优化的过程中引入禁飞区约束。禁飞区即飞行器不允许飞入的空域，譬如防空识别区、导弹拦截区等，在设计轨迹的时候必须要绕过禁飞区。

根据需要，确定禁飞区路径约束为：

C(x(t),u(t),t)≤0,t∈[t0,tf]

(5)

通常情况，热流、动压和过载被认为是路径约束，以不等式的形式给出，比如说热流约束表示为：

(6)

式(6)中，RN为滑翔飞行器头部热流驻点半径；ρ0为海平面标准大气密度；Vc=7.8×103m/s为地球第一宇宙速度；K1为常数。

过载约束的表达为：

(7)

动压约束的表达式为：

(8)

1.3 禁飞区参数模型构建

禁飞区的形状不尽相同，可以分为规则形状禁飞区和不规则形状禁飞区。常见的典型规则形状禁飞区包括圆柱形、球形(半球形)、椭圆柱形和椭球形(半椭球形)，不规则形状禁飞区可以通过多种、多个典型规则形状的禁飞区形状的组合来表征。下面通过具体分析，分别建立参数化数学模型来实现多种禁飞区覆盖范围的描述。

1.3.1 球体、椭球体禁飞区

在进行禁飞区坐标表示时，对于椭圆柱形禁飞区，首先确定禁飞区的中心点位置N的坐标，该点一般位于地球表面，一般以该点在地心赤道坐标系下的坐标(rN,λN,φN)为准。再以N点为原点建立禁飞区直角坐标系，其中Nx轴沿着椭圆柱面的短半轴方向，Ny轴垂直于水平面指向天，Nz轴沿着椭圆柱面的长半轴方向，Nx轴与正北方向的夹角为αN。参照文献[13]，禁飞区中心点在地心赤道坐标系下的坐标可以表示为：

(9)

式(9)中，re为地球半径；(r,λ,φ)为飞行器在地心求坐标系下的坐标。

由禁飞区坐标系到地心赤道坐标系的变换矩阵为：

F=F2[-(90°+αN)]F1[φN]F3[λN-90°]

(10)

其中

(11)

(12)

(13)

因此，飞行器在禁飞区坐标系下的坐标(xN,yN,zN)可以表示为：

(14)

由此，椭球体禁飞区参数坐标可以表示为：

(15)

式(14)中，a、b分别为椭球赤道面的长半轴和短半轴长度；c为椭球的极半径长度。图1为椭球体禁飞区示意图。

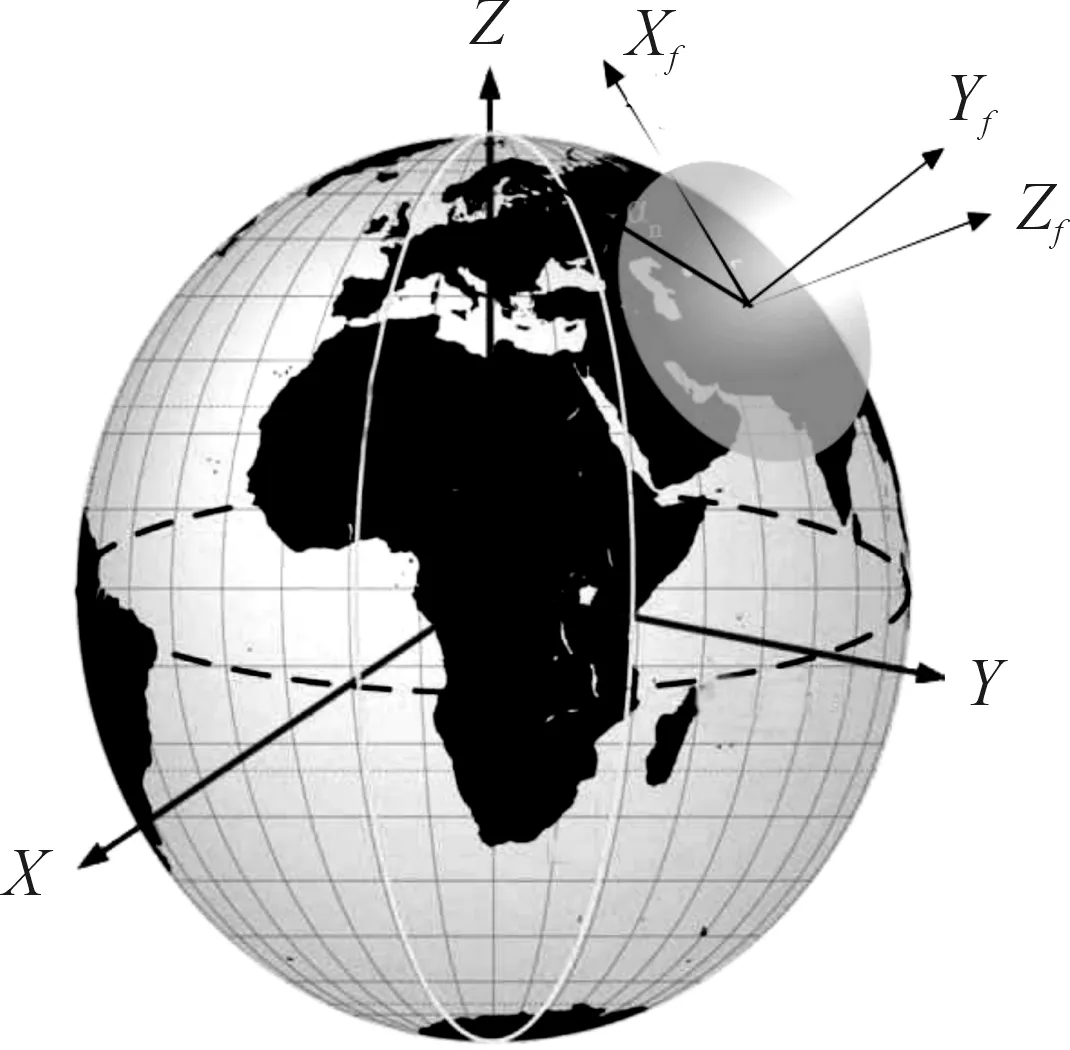
图1 椭球体禁飞区示意图

当a=b=c时，椭球球心至椭球表面各点距离相等，此时的椭球体禁飞区退化成球体禁飞区，其半径r=a=b=c。

1.3.2 圆柱、椭圆柱体禁飞区

令式(14)中的椭球体极半径长度c=∞，此时的椭球体就变成了椭圆柱体，可以表达为：

(16)

椭圆柱体切面的长半轴、短半轴分别为a、b，分别与禁飞区坐标系Nxf、Nzf轴重合。若禁飞区有具体的高度界限，则可通过限定y的取值范围来实现表示。特殊地，当椭圆柱体的长半轴和短半轴相等时，即a=b，此时的椭圆柱体即是圆柱体，其切面半径r=a=b。图2为椭圆柱体禁飞区示意图。

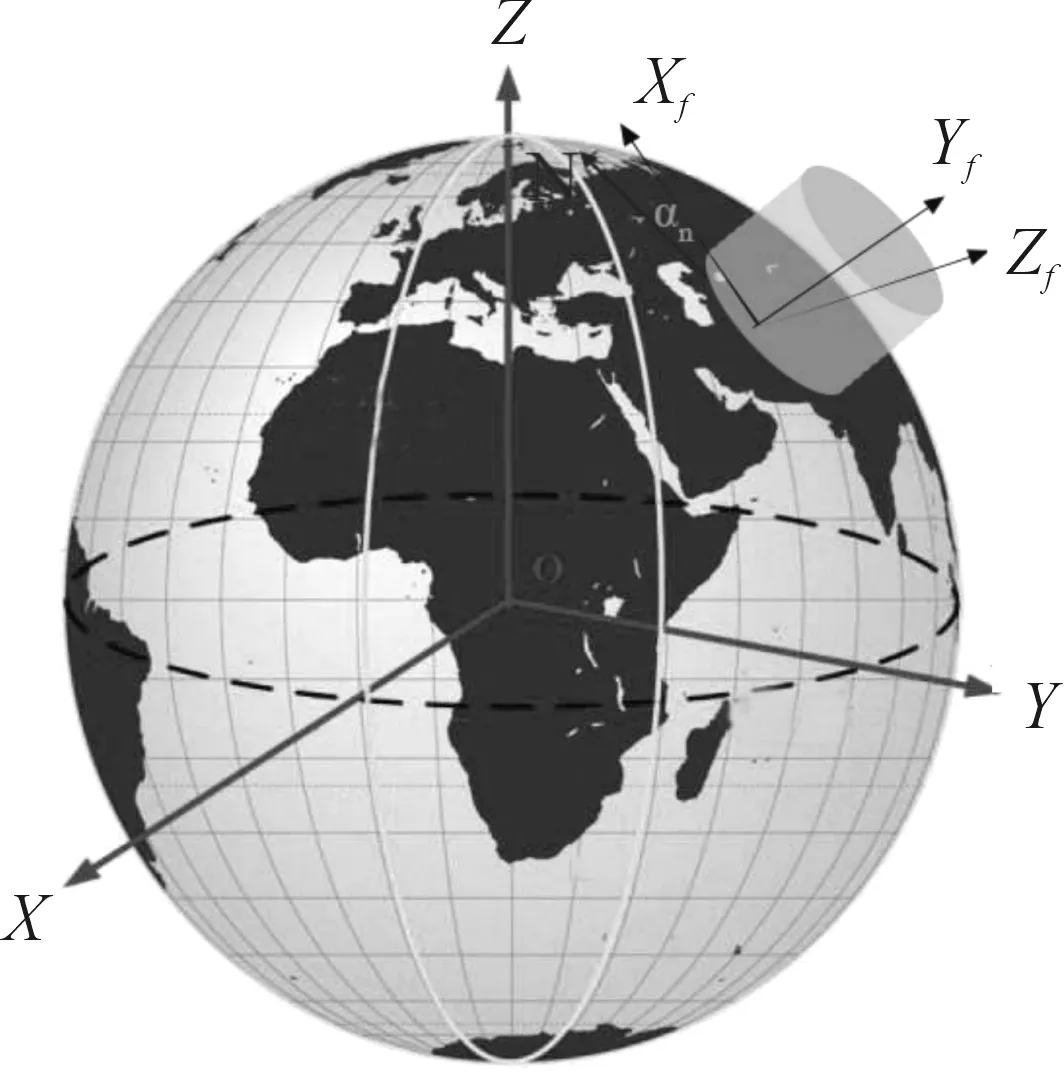
图2 椭圆柱体禁飞区示意图

禁飞区形状具有多样化的特点，而其他形状的禁飞区可以类比以上两种情况得出相关表达式，此处不再赘述。

飞行器再入时，其轨迹不得进入禁飞区内部，即飞行器与禁飞区的最短距离必须保持为正值，设L(x(t),t)为飞行器到禁飞区的最短距离，则禁飞区约束可以通过代数表达的方式计入计算，即使得L(x(t),t)≥εn。

2 自适应伪谱法解决最优控制问题

2.1 自适应网格规划策略

在判断是否需要细化网格区间时，要确定误差评估准则。在自适应伪谱法评估的基础上，将动态约束和路径约束方程在配点间的契合程度作为误差评估标准[14]。

设[tk-1,tk]为第k个子区间，区间内共有Nk个配点数。取相邻配点之间的等间距分布的s个点作为误差评估采样点，有：

(17)

式(17)中，i=1,…,N(k)；n是子区间内配点间评估采样点的序数。评估采样点的数量选取可以随机确定，但不宜过多，一般取为2～4，因为过多的采样点会造成计算代价的增加，而传统的hp自适应伪谱法在采样时仅仅取相邻配点的中点作为采样点，其误差评判规则不够精确。

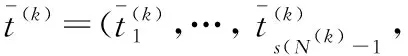
(18)

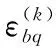
2.2 考虑禁飞区的再入轨迹优化求解策略

高超声速飞行器再入轨迹的设置需要考虑复杂约束，而轨迹优化问题经过自适应伪谱法的离散化后，最终轨迹的状态变量和控制变量也变成了随配点排布的离散量。而在复杂约束中，比如禁飞区约束，是针对连续的轨迹进行约束的。因此，经过自适应伪谱法解算出的最终结果，只能保证轨迹中的每个配点的状态变量满足复杂约束，而配点间的轨迹却可能不满足题设的约束条件。2.1节针对自适应伪谱法进行了改进，加入多误差评估点插值和网格再细化的评判决策，最优轨迹在精度上有了较好的进步，但改进算法仍然不能完全解决禁飞区连续性约束的问题。如图3所示，误差评估点之间的轨迹可能会越过禁飞区边界，使得轨迹优化问题不满足禁飞区约束。

图3 配点间不满足禁飞区约束的情况

为了使得配点之间的轨迹满足禁飞区约束，防止出现图2的情况，就必须对禁飞区周围的配点进行进一步优化。可以利用2.1节，调节自适应网格细化策略的误差门限值ε来实现，下面列出具体方案。

取L(x(t),t)最小的区间进行条件验证。2.1节中，自适应伪谱法网格细化过程中，定义区间内的最大曲率向量为ρ，对应的，在L(x(t),t)上的最大曲率为ρl，则L(x(t),t)内，即由区间初始点Mk到区间终止点Mk+1轨迹的最大曲率半径为：

(19)

由于飞行器再入过程中速度很快，每个子区间时间段很小，很难有大幅度的矢量角度变化，因此可将子区间内轨迹的曲率半径看作恒定。以曲率半径rl为半径，作通过子区间轨迹初、末两点Mk和Mk+1的劣弧Cl，定义Cl围绕线段MkMk+1形成空间为最大轨迹空间。由于通过区间内轨迹的曲率必然比ρl小，可知最大轨迹空间可以包含飞行器在区间内所有可能的轨迹。

考虑Ξk为第k个区间内最大轨迹空间与禁飞区的距离，则若保证Ξk>ε，即可满足L(x(t),t)>ε。

若取极端条件，即区间内的最大轨迹空间与禁飞区界面迫近相切时，此时轨迹满足下式：

l(x)>L(x(t),t)>o(x)

(20)

式(19)中，O(X)=Ξk→0+。设区间中轨迹初、末两点Mk和Mk+1的直线距离为sl，则sl≈l(x)，且有

(21)

至此，就可以保证再入轨迹全部满足禁飞区约束。这一方法对解决离散问题路径约束问题有较好的推广性。

3 仿真算例与分析

本节的仿真实验，使用CAV-H飞行器的数据进行模拟飞行，优化仿真的硬件环境也是相同的。现将轨迹优化问题的条件描述如表1-3所示。

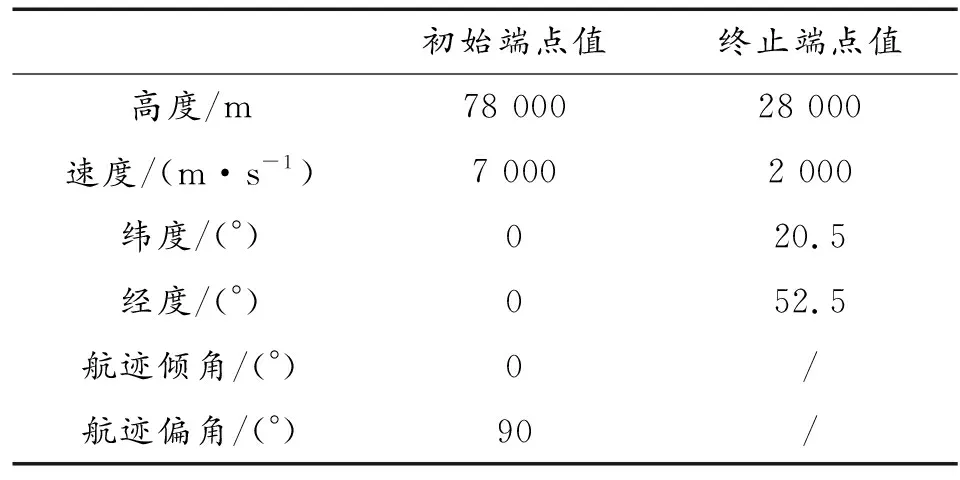
表1 状态变量的端点状态参数

表2 热流率、动压、过载约束

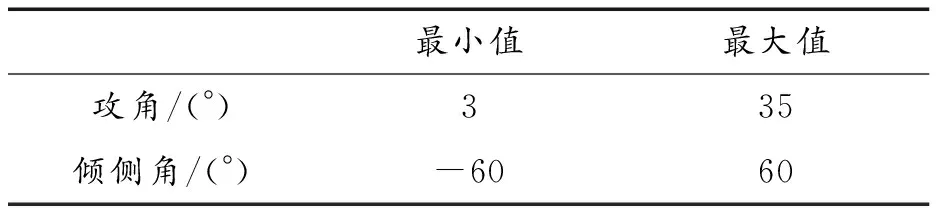
表3 控制量的取值边界

除此之外，还要设立禁飞区约束。在得出上述条件的仿真轨迹后，在原始轨迹和优化轨迹可能穿过的地域设立禁飞区约束，本节选取飞行实际情况中最为典型的禁飞区约束类型，针对椭圆柱体禁飞区约束和椭球体禁飞区约束模型进行仿真实验。

建立2个区域的圆柱体禁飞区约束如下：

1) 以地球坐标系(30°E，5°N)为禁飞区水平切面中心，设立半径r1=150 km的圆柱体禁飞区。

2) 以地球坐标系(25°E,5°N)为禁飞区水平切面中心，设立半径r2=300 km的圆柱体禁飞区。

为了求解方便，两个圆柱体禁飞区的高度可以定为飞行器最高的飞行高度，即70 000 km。

建立1个椭球体禁飞区约束如下：

1) 以地球坐标系(40°E,6°N)为禁飞区水平切面中心，椭球体禁飞区的长半轴a=440 km沿纬线方向，短半轴b=220 km沿经线方向，极半径c=40 km垂直水平面指向天。

加入禁飞区约束后，得出原始轨迹和优化轨迹的状态变量随时间变化如图4所示。

由仿真实验结果可以清晰看出，优化后的轨迹完成避障任务时，弹道的跳跃性更强，每次跳跃幅度比原始轨迹的跳跃幅度高出50%以上，但最终在飞行精度上可以达到目标点。优化前后的速度和弹道偏角变化区别不明显，基本符合预期要求。

优化前后的经纬度运行图如图5所示。

由图4可知，相比于原始轨迹，优化后的轨迹可以完全避开禁飞区区域，通过引入最大轨迹空间的概念，使得轨迹优化配点间的轨迹完全处于禁飞区外部，通过设定误差门限值，能够在避障的同时完成最优指标。从图5可以看出，在距离禁飞区较近的轨迹区间内，其配点较为密集；在距离禁飞区较远且轨迹平滑的阶段，其配点较为稀疏。

优化后轨迹的控制变量与时间的关系曲线如图6所示。由图6(a)可知，优化后的轨迹在多数时刻内攻角控制量略微偏大，大攻角飞行可能会影响到升阻比，进而影响热流率参数，但优化方案的攻角仍在允许范围内，飞行中25°以内的攻角不易产生交叉耦合现象。图6(b)显示优化方案通过调节飞行器的倾侧角实现程序转弯，从而绕过禁飞区。

图4 禁飞区约束下的轨迹状态

图5 飞行器航行轨迹

图6 控制变量与时间的关系曲线

优化后轨迹的热流量、动压值分别如图7和图8所示。

图8 优化轨迹的动压

可以得出，优化后的轨迹基本满足热流量和动压约束。相比于原始轨迹，优化轨迹在实现越过禁飞区转弯时的热流量会比较大，转弯后则与原始方案基本持平，飞行的动压约束在最终状态达到峰值，主要是因为再入末端的空气密度较大，使得动压在低空飞行时猛增，总体来讲，实验数据在可接受范围内，可以完成高超声速飞行器再入快速轨迹优化任务。

4 结论

通过对自适应伪谱法进行改进，综合在配点间设立多个误差采样点策略，并提出最大轨迹空间的概念，解决了因问题离散化而导致配点间的轨迹不满足禁飞区和其他路径约束。通过仿真实验可知，求解策略可以求得复杂约束条件下的轨迹最优解。通过对比分析优化前后方案，突出了采用最大轨迹空间法的优化效果。