基于大视场反卷积的天文图像叠加方法∗
2019-02-23蔡博君孙荣煜王伟男
蔡博君 贾 鹏 孙荣煜 王伟男
(1 太原理工大学物理与光电工程学院 太原 030024)
(2 Department of Physics,Durham University,Durham DH13LE)
(3 中国科学院紫金山天文台 南京 210008)
1 引言
地基光学望远镜作为天文观测的主要仪器,其口径D的大小直接决定了光学系统对天体细节的分辨本领与对暗弱天体的探测灵敏度.望远镜的分辨本领指的是分辨角δ的倒数,望远镜口径D越大,δ越小,所能分辨的最小角距离越小,空间分辨率也越好.望远镜的灵敏度即集光力,与口径的平方D2成正比,D越大,集光力越强,从暗弱目标上聚集的光就越多,就能对更微弱的目标进行测光和成像.所以,望远镜的口径D越大,其探测能力就越好.
但是,望远镜的造价P∝D2.8[1],这意味着望远镜口径扩大1倍,而其造价将提高约6.96倍.而通过几个小口径的望远镜组成4通道望远镜,其造价P∝D2.因此,针对点状暗弱目标探测的任务,大口径望远镜相比4通道望远镜能够更方便地提高灵敏度.
2002年,Fruchter等[2]曾提出,可通过图像配准以及灰度值相加的手段提升图像的质量.4通道望远镜获取了同一天区目标在同一时刻下的多帧图像,对这些图像进行叠加处理后得到的结果,可达到与大口径望远镜相近的灵敏度.2017年,Ping等[3]通过对4通道望远镜的指向模型进行分析,指出望远镜之间存在的指向差异导致望远镜之间的图像存在几何偏差,通过对未安装滤光片的4通道望远镜图像进行配准校正并直接叠加,使星象信噪比以及对星象的探测能力得到了提高.但直接叠加图像的像质受多个望远镜中分辨效果最差的望远镜限制,通过在图像复原的基础上进行图像叠加可以提高观测灵敏度.
如果图像背景噪声满足泊松分布,则天文图像成像过程的退化模型可由下式所示的数学表达式来表述:

传统的反卷积算法假设整幅图像中各点的PSF不存在差异.由于PSF随时间和视场位置变化,使用同样的PSF对此类图像反卷积的效果不佳.1978年,Trussell等[4]提出图像分块复原的方法,该方法将图像划分为多个子块,认为每1块子图的PSF是一致的,通过对子图进行反卷积,再将子图拼接到一起,得到复原后的清晰图像.但是,这种方法的图像切割过程随意性比较大,不能反映PSF的真实变化.
考虑到4通道望远镜大多都是大视场观测系统,其PSF也是随视场变化的.所以,本文先对PSF进行聚类分析,基于PSF的聚类结果对图像进行分割,再使用分类后的PSF与分割后的图像反卷积.然后将反卷积后的复原图像拼接成1个整体,降低PSF差异性对图像叠加带来的影响.此外,考虑到4通道望远镜多个镜筒之间存在指向偏差,我们对反卷积复原后的结果进行了亚像素配准,以矫正望远镜的指向偏差,实现4通道望远镜的图像复原叠加.
2 大视场望远镜的分区反卷积算法
作为1种大视场望远镜,4通道望远镜的观测图像受不同视场区域轴外像差的影响.获取图像的PSF差异具体体现为:在单帧图像中,图像不同视场区域的PSF具有差异;在多个望远镜同一时刻下观测到的图像之间,同一区域的PSF也具有差异.如果将PSF具有差异的图像进行叠加,得到的图像像质会降低,导致图像的信噪比降低,影响4通道望远镜图像叠加的效果.而通过分区反卷积算法可以提高像差的一致性和图像的信噪比.
本文提出的大视场望远镜分区反卷积算法的整体实现过程包括4个部分,分别是:数据预处理、PSF聚类、图像分区和图像分区反卷积.
2.1 数据预处理
星象的PSF反映了清晰星象在退化过程中的光度分布,而暗弱星象由于亮度过低,所提取的PSF边缘往往会被背景和噪声淹没,导致暗弱星象的PSF缺乏足够的光度分布信息,在很大程度上会影响反卷积的复原精度,降低复原结果的分辨率.所以在选取聚类样本的过程中,需要对PSF数据进行预处理.为了弥补暗星PSF信息缺失的问题,剔除掉冗余信息及噪声带来的干扰,我们根据图像中星象的灰度值,在图像不同位置的星象中选取最大灰度值前85%的星象作为亮星,对从这些亮星所提取的PSF数据集进行PCA(Principal Component Analysis)降维处理.该过程实际上是1个将高维数据向低维空间映射的过程,降低了数据的维度,同时提高了接下来数据聚类过程的效率.
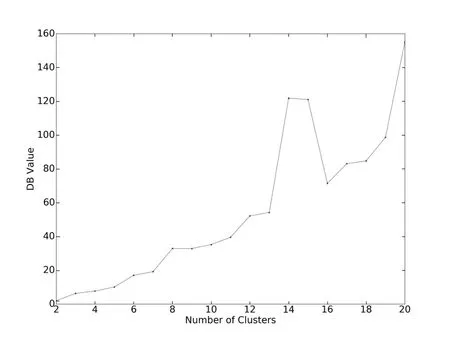
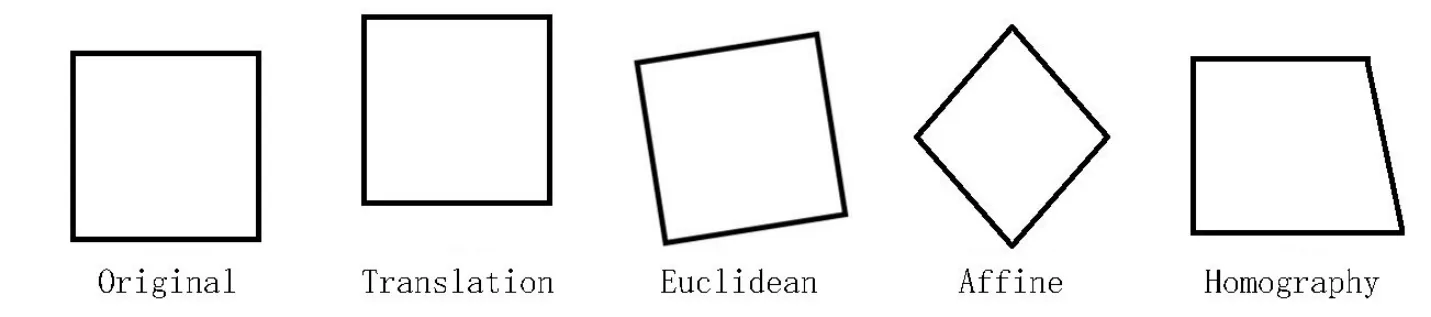
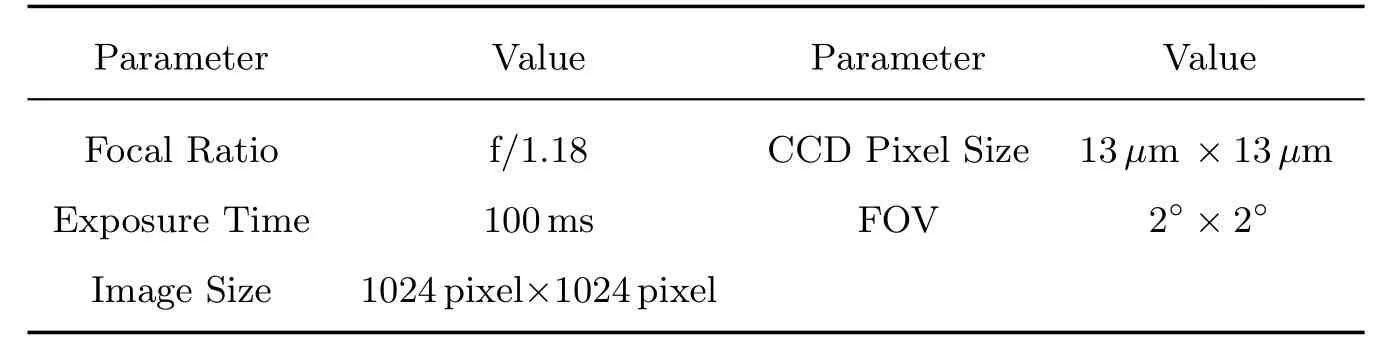
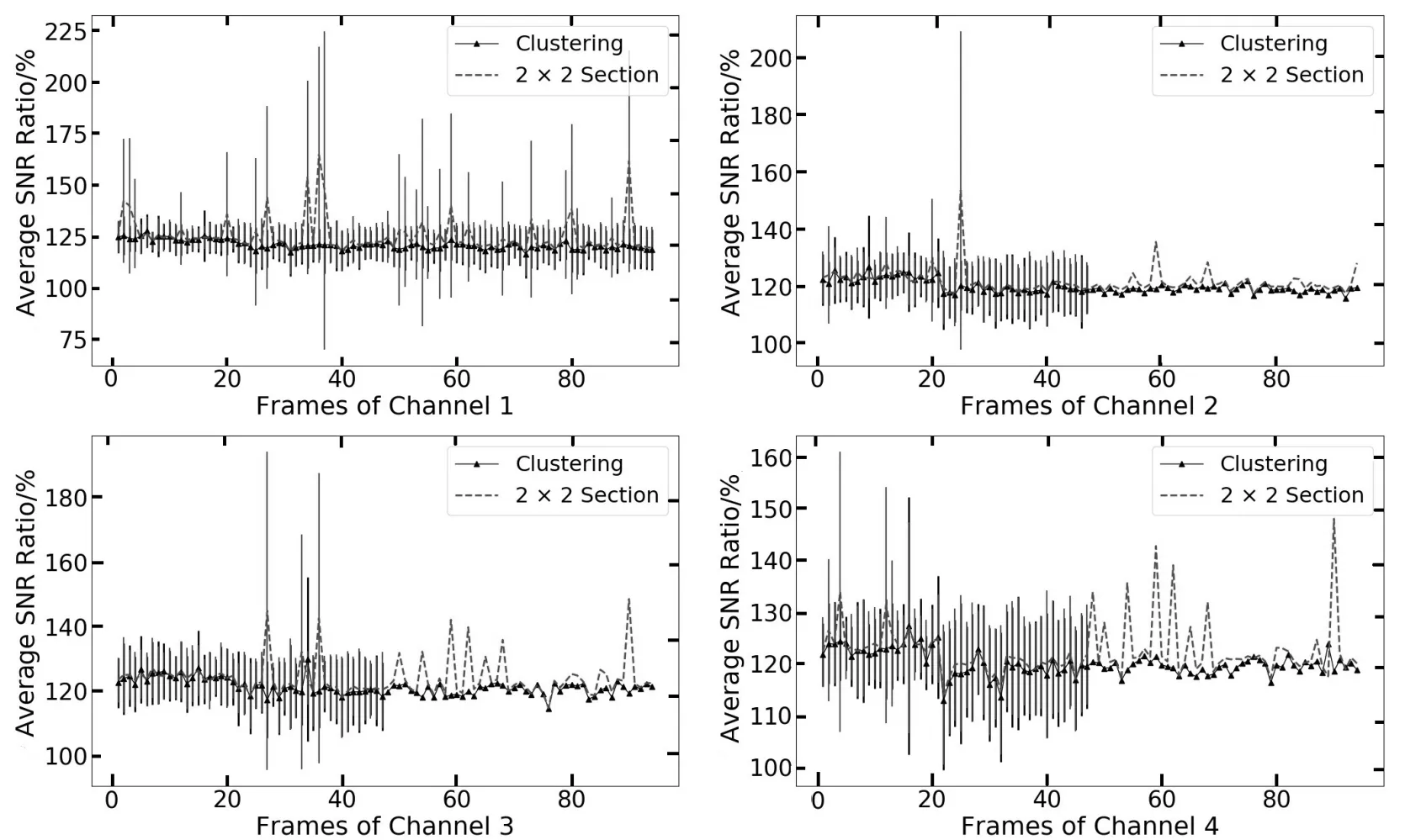
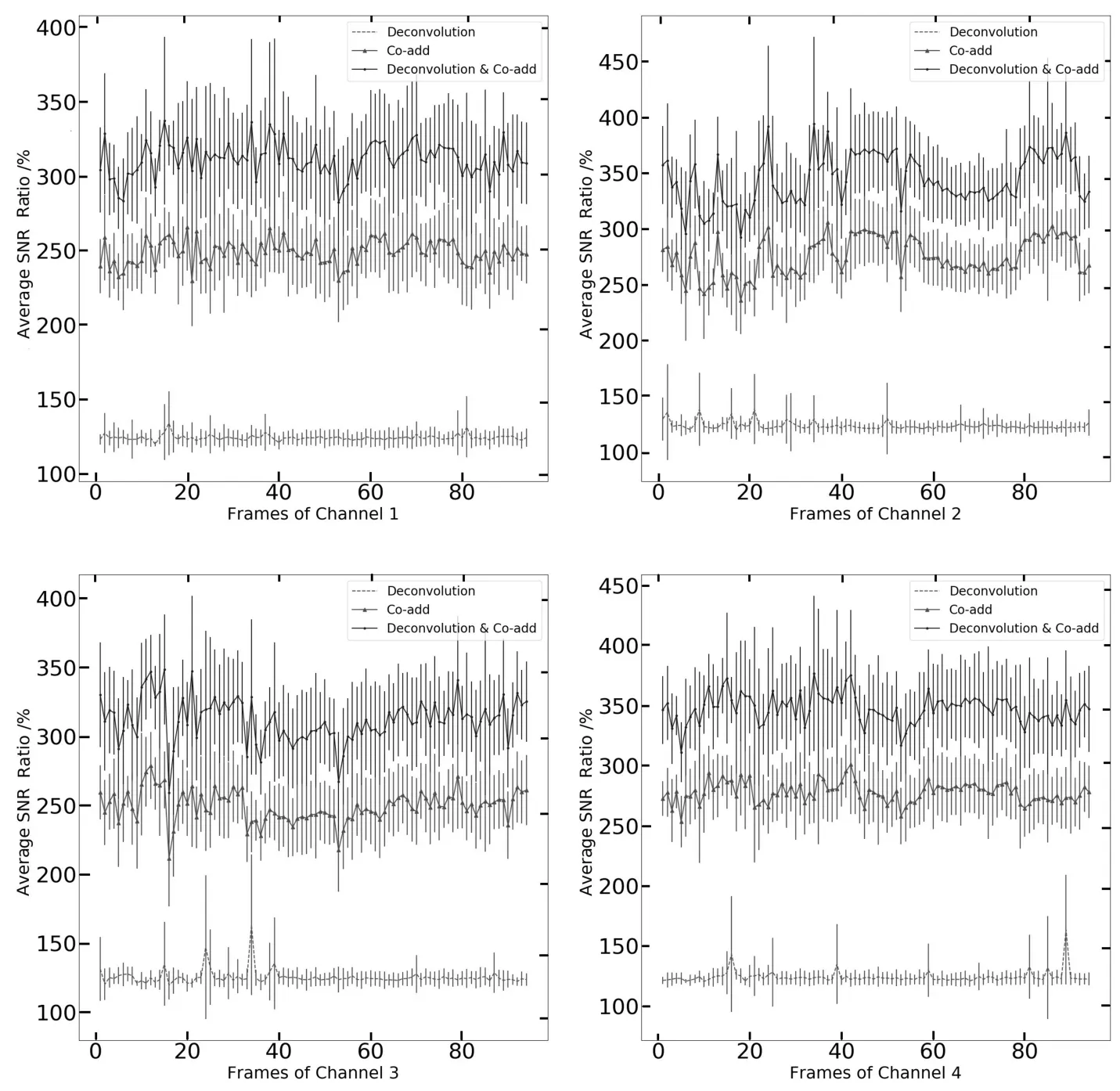
将具有n个特征的PSF数据P={p1,p2,···,pm}利用PCA降维到k维(k (2)用pi− µ替换原来的样本pi,得到新的P={pi|pi=pi− µ,i=1,2,···,m}; (3)求出P的协方差矩阵C,大小为m×m,并求出C按降序排序的特征值(E1,E2,···,Em)与特征向量{e1,e2,···,em}; (4)选前k个特征值对应的特征向量,组成1个m×k的特征矩阵E={e1,e2,···,ek}; (5)得到大小为k×m的降维结果D=E×P.其中D={d1,d2,···,dm}中每1项的大小为k×1,为降维后的PSF数据. PSF间的差异是影响4通道望远镜图像叠加的主要原因,为了根据PSF的差异进行分类,我们将PCA降维后的PSF进行聚类.聚类过程中,划分类数是未知的,可先设定出多个类数,再根据这些聚类结果的评价指标确定出最合理的聚类结果,本文通过SOM(Self-organizing Maps)神经网络进行PSF聚类,用DB(Davies-Bouldin)指数作为聚类合理性的评价手段. SOM神经网络是1种基于生物神经元自组织特性的无监督学习网络.SOM能通过对自身训练,在无监督的情况下实现对输入数据的聚类.其网络结构由输入层与竞争层组成,SOM的学习过程及对PCA降维后PSF数据的聚类过程如下: (1)初始化映射的节点权重向量W,输入降维后的PSF数据D={d1,d2,···,dm},m为PSF数据的个数; (2)计算所有PSF与所有节点权重向量间的欧氏距离,距离最小的节点为获胜节点Wc; (3)以获胜节点Wc为中心,按以下规则更新Wc及其邻域内节点: 其中s表示当前迭代次数,θ(s)表示第s次迭代节点的距离限制,0<θ<1,α(s)为第s次迭代的学习率限制; (4)s=s+1,重复步骤(2),直到s达到迭代上限λ,竞争层输出聚类结果. DB指数是Davies等[6]在1979年提出1种评估聚类的算法,该算法通过数据点间分散程度以及类间距离来评价类间相似度,其定义如(2)式.其中,DBindex是聚类结果的DB指数,N是聚类数,和分别是第i类数据和第j类数据的类内相似度.Mi和Mj分别是第i类数据和第j类数据的类间距离.DB指数计算的是欧氏距离下任意两类别数据的类内距离平均距离之和除以两聚类中心距离的最大值[7],DB指数越小,表示聚类结果的类内距离就越小,类间距就越大,意味着聚类越合理. 本文中的PSF聚类过程由以下两步完成:(1)采用SOM神经网络将PCA降维后的PSF数据事先指定好的类数进行聚类;(2)选择DB指数作为PSF聚类结果合理性的评价指标,计算指定分类数下SOM分类结果的DB指数.选取出DB指数最小的聚类方案为最合理的聚类方案. 如图1,是通过SOM神经网络对52511个PSF数据聚类后计算DB指数的结果,预先设定的聚类数为2–20类.从图1中可得知:当聚类数为2类时,该组数据聚类结果的DB指数是最小的,所以聚类数为2类的聚类结果为该组数据最合理的分类方案. 图1 PSF聚类结果的DB指数Fig.1 DB index of the clustered results of PSFs 根据PSF聚类结果可以对图像PSF一致的区域进行分割,在每个区域分别通过图像复原提高图像质量.为了将复原后的区域整合为1幅图像,本文先按照PSF的聚类结果对图像进行分区,再将复原图像按照分区结果来分割,最后将对应PSF区域的复原图像进行拼接. 考虑到PSF分类实际上是以PSF作为参考,对图像PSF一致区域做出的初步划分,PSF来源于图像中不同位置的星象,而仅凭星象是无法覆盖整个图像区域的,所以,可以利用区域生长算法来实现图像的分区.根据事先设定好的生长规则以及所给的初始标签种子,区域生长算法将遍历图像中所有像素,并按照生长规则把像素种子周围像素邻域中与标签种子具有相似性质的像素合并到标签种子所在的区域中,当图像中没有像素满足加入某个区域的条件时,区域生长将停止[8−9].区域生长算法的生长规则可以按要求指定,只需给出初始的标签种子就能将图像基于标签种子的位置分割成多个子图,并且同一区域的像素将具有相同属性特征. 本文将PSF的聚类结果在图像中的位置作为初始的标签种子,利用不同视场区域PSF的差异性结合区域生长算法对图像进行分区.区域生长算法按以下流程实现: (1)建立与图像大小一致的全零矩阵作为区域分割的掩膜矩阵; (2)读取并设置种子点,即把标签种子在全零矩阵中对应位置的像素点置为种子的标签值; (3)以种子点为起点,遍历掩膜矩阵中种子点的8-邻域,将8-邻域内未获得标签的像素点的标签置为当前种子的标签值,并把该像素点做为新的种子点继续扩展; (4)重复步骤(3),直至掩膜矩阵中的所有像素点都获得标签. 由于选取PSF聚类结果作为初始种子,图像区域分割的结果可以反映出图像中不同类别PSF对应的区域.将该结果作为掩膜矩阵可以实现基于PSF类别的图像分区. 为了提高PSF的一致性,通过图像反卷积对图像进行处理.本文利用SGP(Scaled Gradient Projection)算法对退化图像进行反卷积,再结合掩膜矩阵实施图像的分区与拼接.2009年,Bonettini等[10]提出了利用SGP算法进行图像复原.2015年,邵云龙[11]利用程序仿真,通过计算复原结果的峰值信噪比和结构相似度,指出SGP算法具有复原精度高、迭代效率快等优点. SGP算法考虑的是图像去模糊过程中特殊约束下的最小化问题,根据(1)式所给出的退化过程的数学模型,SGP算法求解出x迭代最小化的估计,如下所示. 上式中x为图像的复原结果,是清晰图像的近似估计.J(x)表示为Ax+yg与y的Kullback-Leible(KL)散度,反映的是两者之间的差异,其定义如(4)式所示. SGP算法在计算x的过程中,每次迭代都要计算投影其中Ω为1个凸集,f为Ω上的函数,为Dk的逆,α为迭代步长,k表示当前迭代的次数,按照Barzilai等[12]所给的更新规则,可加快梯度方法的收敛速度;Dk为缩放矩阵,的海森矩阵的逆,而在实际情况中,为了优化迭代效率,我们选择1个适当的阈值L,采用(5)式所示的策略更新缩放矩阵Dk中的元素: SGP算法计算频域下估计的清晰图像x与退化过程的影响A的乘积,结合频域下实际的退化图像y,将两者的KL散度作为评价函数.本文将聚类后的每一类PSF的平均PSF都作为先验PSF,利用SGP算法将退化图像与先验PSF进行反卷积,最终得到信噪比较高、降低了PSF差异性的复原结果. 通过掩膜矩阵与复原后图像相乘,保留对应掩膜矩阵区域的结果,实现复原图像的分区,再将分区后的结果按照对应位置进行拼接,就可以实现图像的分区反卷积.经上述过程处理后,不同视场PSF存在差异的影响被降低,多个望远镜之间PSF具有差异的问题也得到改善. 理论上,4通道望远镜的多个镜筒指向同一天区,图像直接按照对应坐标叠加即可;但是,由于跟踪和CCD安装过程中存在偏差,需先分析不同通道图像之间存在的几何偏差,再通过几何变换修正复原图像的偏差,最后对复原结果进行叠加. 常见的图像几何变换模型可分为:平移变换、欧几里德变换、仿射变换和透射变换,如图2所示. 图2正方形图像通过不同变换模型的变换结果Fig.2 The results of a square image transformed by different transform models 图2中的任何一种几何变换过程都可以通过1个3×3的变换矩阵来实现,如(6)式所示[13]: 在(6)式中,原始图像中的点在其所在平面的点坐标d=(x,y,z)T,经1个3×3的变换矩阵M便可得到某种几何变换后在另1个平面下的点坐标d′=其中d、d′为2维平面上点在3维空间的齐次表示,(x,y)和(x,y)为两个不同2维平面的点坐标,z和z都为1.m13和m23分别为x和y方向的平移量,设定这两个值可实现平移变换;m11和m22分别控制变换过程x和y方向上的缩放尺度,结合m12和m21可实现欧几里德变换;将平移变换和欧几里德变换的6个独立参数结合,就可以实现仿射变换;m31和m32为x,y方向的视角参数,m33为比例参数,一般情况取1,结合仿射变换的6个参数可实现3维物体在1个2维平面上的投影,即透射变换.透射变换包含其他所有几何变换所需要的参数,其他几何变换都能通过透射变换来完成.变换矩阵M中的9个参数分别包含几何变换过程中平移、旋转、切变、尺度和视角方向的信息,当M为单位矩阵时,图像不会发生任何变化. 多个望远镜之间的偏差包括由望远镜安装带来的平移和旋转偏差、望远镜调试带来的尺度偏差以及CCD轴面倾斜带来的视角偏差,导致CCD上观测图像实际中心偏离预期的中心.并且,尺度偏差造成几何变换模型中所有参数都需要经过尺度缩放来矫正1https://docs.opencv.org/2.4/modules/calib3d/doc/camera calibrationand3d reconstruction.html.通过求解几何变换矩阵进行透射变换,将一个望远镜图像投射到另一个望远镜图像所在的视平面,能够实现望远镜之间图像偏差的修正. 在确定了图像间的几何变换后,就可以通过对应的几何变换实现图像间的配准.作为图像配准过程中的重要一环,变换矩阵的准确度将直接影响到图像叠加的效果,准确度过低将导致叠加结果出现“重影”现象.为保证图像配准的准确度能达到图像叠加所需的要求,将图像的增强相关系数(EECC)作为评价望远镜图像配准准确程度的指标[14],EECC可以反映两个图像对象间相关关系程度.EECC的计算式如(7)式所示: 在同一时刻下的观察数据中,选取信噪比最高的图像作为基准图像.其中,是基准图像向量化后的结果,是图像i向量化后的结果.在梯度空间中,图像的灰度梯度向量按照步长迭代,EECC随迭代步长变化而变化.设定图像间的增强相关系数迭代终止的准则,当EECC满足配准精度时,程序终止,返回满足配准精度的变换矩阵,实现望远镜图像之间几何变换矩阵精度的控制. 4通道望远镜不同通道使用不同的滤波片,图像间对比度会存在差异,而EECC与偏移量和增益的改变无关,算法受图像亮度及对比度的影响不大.通过设置ECC算法的迭代步长,可保证望远镜CCD图像的配准结果达到亚像素级的精度.对配准结果进行图像叠加即可得到最终的复原叠加结果. 本文中处理的数据是4通道望远镜于2012年9月8日至9月10日观测的共计4×537张图像,相关参数如表1所示. 表1 图像及成像系统参数Table 1 Parameters of image and imaging system 本文中对4通道望远镜图像的叠加工作按以下步骤完成. 首先对退化图像进行配准.由于CCD传感器在进行图像采集过程中,受温度等因素影响,其输出的信号中掺杂了各种噪声以及干扰.这些噪声和干扰使得图像主要信息被高频噪声淹没、星象轮廓模糊不可辨,增加了图像高精度配准工作的难度.而图像锐化是一种通过高通滤波器针对图像的轮廓、边缘处进行增强的操作,通过图像锐化可弥补星象轮廓被高频噪声淹没的缺陷.在进行图像配准时,从锐化处理后的退化图像中选取信噪比(SNR)较高的图像作为基准图像,利用ECC算法计算出矫正图像所需要的变换矩阵,并将其他通道的退化图像依次利用透射变换投射到基准通道所在的视平面上. 然后对图像进行分区反卷积.先从配准后的图像中提取出PSF,并对得到的PSF进行PCA降维,将降维后的数据通过SOM神经网络聚类,设定分类类数为2–20类,利用每次分类结果的DB指数确定最佳分类数.按最佳分类数下的分类结果对图像分区,然后通过SGP算法将分割后的图像与分类后对应的PSF进行迭代反卷积,最后将反卷积结果进行分区和拼接.值得注意的是,反卷积迭代次数过高会导致图像发生过迭代,为避免此现象,本文中将SGP算法迭代反卷积次数设定为5次.将分割图像反卷积的结果拼接成1个整体,整个过程如图3所示. 经历以上步骤处理后,对处理后的图像进行叠加.实现4通道望远镜的反卷积叠加,结果如图4.本文中所有的天文图像是使用SAOImage DS92http://web.oapd.inaf.it/poe/mis/ds9reference/mscale.html软件经zscale后的显示结果. 通过PCA降维后的特征值矩阵与特征向量,可以重构出PSF数据,通过比较重构数据的特征与SOM聚类后数据的特征验证SOM聚类的合理性,如表2所示. 表2 PSF质心对比Table 2 The comparison of PSFs’centroid 图3 4通道望远镜的分区反卷积过程.(a)PSF分类结果;(b)图像分割掩膜;(c)、(d)分割图像的反卷积结果;(e)分割反卷积图像拼接结果.Fig.3 The sectioned deconvolution process of a quad-channel telescope.(a)The clustered result of PSFs;(b)the mask of image section;(c),(d)the deconvolution results of sectioned images;(e)the images after sectioned deconvolution. 图4 4通道望远镜图像反卷积及叠加结果.(a)退化图像;(b)反卷积图像;(c)反卷积后叠加图像.Fig.4 The image deconvolution and co-adding results of the quad-channel telescope.(a)The degrade image;(b)the deconvolution image;(c)the co-adding images after deconvolution. 表2中的Cluster 1和Cluster 2是两个不同聚类的原始PSF的质心值和均方差,Reconstruction 1和Reconstruction 2是利用PCA重建的PSF的质心值和标准差.对于低采样率下的PSF,质心值能够粗略反映出PSF的形态差异.通过比较我们发现,聚类结果与PSF降维重构结果的质心坐标均值与均方差,两者的质心分布基本一致,可得知PSF降维数据中包含了原始PSF的形态特征.从表2的对比结果中可以看出SOM实际上是根据PSF的形态特征进行聚类的. 根据图4的复原结果可以看出,SGP反卷积结果的星象轮廓在视觉效果上比退化图像更为显著;在进行叠加后,星象灰度值的提高远大于背景噪声灰度值的提高,图像背景噪声被抑制,暗星的视觉效果更为明显. 对反卷积及叠加处理得到的结果,从星象信噪比的提升以及星象探测能力两个方面进行分析. 为了客观评价处理后星象的观测效果,采用星象信噪比分别对退化图像和处理结果进行评估.以星象坐标为中心,在星象坐标周围划分1个20×20像元数的区域,求该区域的信噪比即为星象信噪比.星象信噪比定义[15]如下: (8)式中F为星象区域中像素光通量的总和,b为背景的灰度均值,σ为背景的标准差,Nphoto为星象区域中像元的个数.在一定程度上,星象信噪比的高低可以体现出图像的品质,其值越大,说明星象受噪声影响越小,观测质量越好. 比较本文反卷积方法的结果和传统的2×2分块反卷积的结果,如图5及表3所示. 表3中Cl1/Cl2/Cl3/Cl4是聚类分区反卷积算法的结果,S1/S2/S3/S4是2×2分区反卷积算法的结果.从图5和表3中可以观察到:总体上,经过反卷积之后,两种方法都可以提高图像SNR.但是,直接分区法获取的图像SNR提高率方差较大,而且在部分通道的图像上出现了SNR下降的情况,我们PSF聚类复原的办法,对于图像提升比较稳定. 以我们的PSF聚类复原方法和图像叠加方法为基础,对94组退化图像及其反卷积结果、叠加结果和反卷积叠加结果中3888个星象的信噪比和信噪比提升倍率进行统计. 表4为图像在进行不同处理后的星象信噪比数据统计结果.其中C1/C2/C3/C4为4个通道的原始图像,D1/D2/D3/D4为反卷积图像,C为直接叠加图像,D & C为反卷积叠加图像.图6为图像的星象信噪比提升率的均值统计图,上下限误差为图像中星象信噪比提升率的标准差.表4的星象信噪比均值与图6的对比结果都反映出叠加操作使星象的信噪比均值大幅提升,在结合了反卷积处理后,星象的信噪比均值提升更为显著.表4中均方差反映出不同处理后信噪比变化的波动. 图5 不同分区方法的星象信噪比倍率均值对比Fig.5 The comparison of stars’averaged SNR ratio in different section methods 表3 不同分区方法下反卷积结果的信噪比倍率均值统计Table 3 The statistics of deconvolution’s averaged SNR ratio in different section methods 表4 星象信噪比统计Table 4 The statistics of stars’SNR 理论上,通过对同一区域灰度值的叠加,将会提高暗星的亮度和观测效果.我们利用SExtractor,通过阈值分割结合连通域提取的方法提取出图像中的星象目标[16].方法如下: (9)式中std为图像灰度矩阵的均方差,median为图像灰度矩阵的中位数,k为1个常数,本文中k取1.5.设定这样的阈值作为图像背景值,如(10)式所示,设定连通域大小滤去孤立的高频噪声点,当连通域灰度值大于背景值则被当作星象被提取出.提取结果如图7所示. 图6 星象信噪比倍率均值比较Fig.6 The comparison of stars’averaged SNR ratio 对退化图像基准图像、叠加图像及反卷积叠加图像的星象提取结果加以统计,结果如表5和图8所示. 图7 退化图像与复原图像的星象提取结果.(a)退化图像;(b)反卷积图像;(c)叠加图像;(d)反卷积叠加图像.Fig.7 The star extraction results of degrade and restoration images.(a)The degrade image;(b)the deconvolution image;(c)the co-adding image;(d)the deconvolution and co-adding image. 表5中星象提取的对比结果表明:不同通道的望远镜之间的几何偏差,导致同一时刻下星象提取的结果存在一定的差异.分析图8的结果,通过配准消除不同通道间的几何偏差后,直接叠加的星象提取结果约为其他通道星象提取结果的1.5倍,反卷积叠加的星象提取结果约为其他通道提取结果的2倍.望远镜的灵敏度通过反卷积叠加得到较大的提升.再结合图6中的反卷积叠加结果来看,原本被噪声淹没的暗星经过处理后可被探测到,暗星变得更加清晰,进一步提升了4通道望远镜的探测能力. 本文研究了4通道望远镜多色观测图像的复原叠加算法,并对2012年9月8日至10日由4通道望远镜拍摄的2148张图像利用本文的方法进行分区反卷积和配准叠加处理,实现了多色观测的大视场天文图像的复原叠加工作.经数据分析,处理后的图像在星象信噪比和成像系统对暗弱目标的探测能力上得到了提升.分区反卷积叠加算法从灵敏度的角度提高了光学成像系统对暗星的探测能力,星象的信噪比得到了提高,本文的工作将对后续多孔径望远镜的图像处理工作具有一定的借鉴意义.2.2 PSF聚类
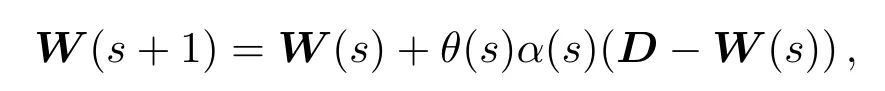
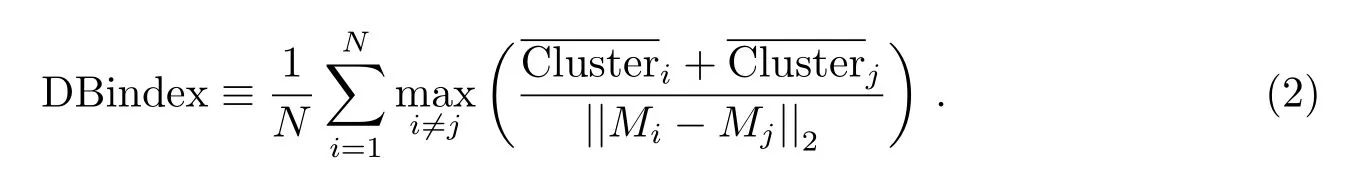
2.3 图像分区
2.4 图像分区反卷积

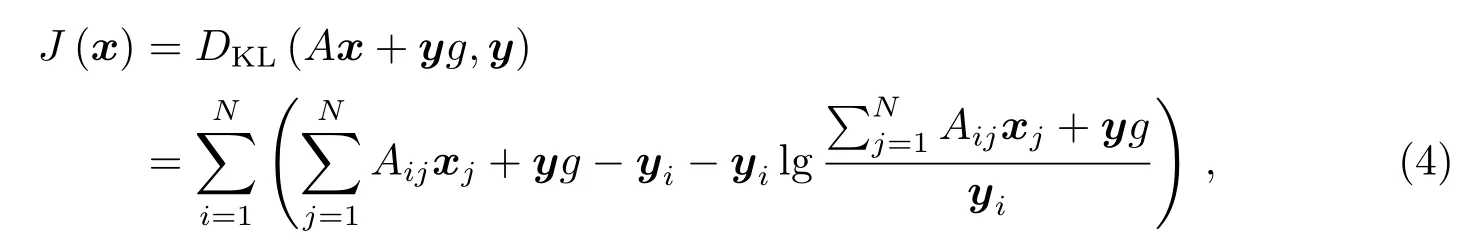
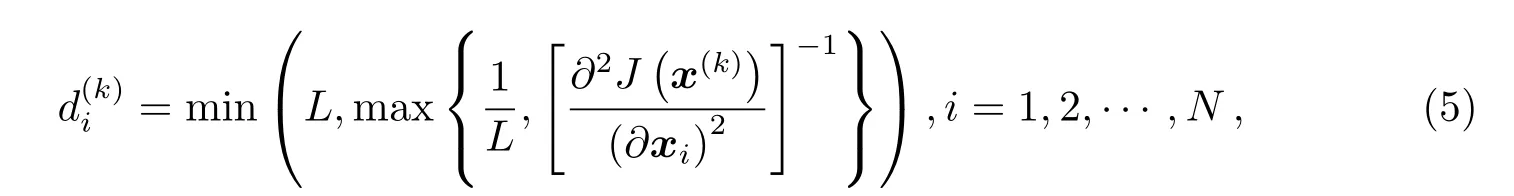
3 亚像素配准叠加
3.1 图像的几何变换
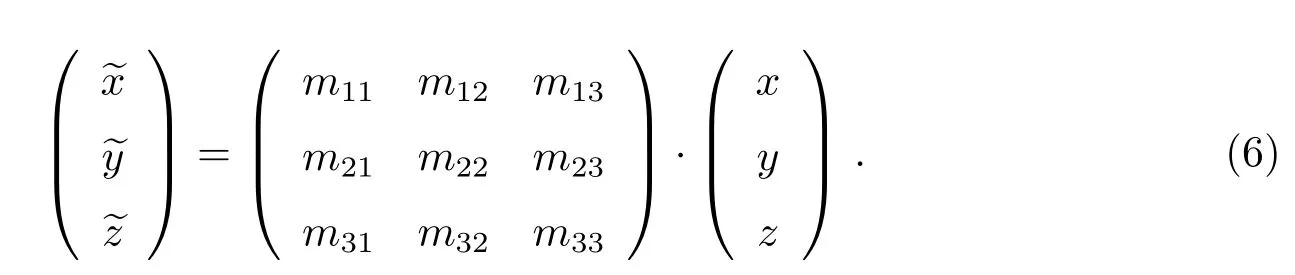
3.2 图像配准与叠加

4 处理过程
4.1 数据信息
4.2 处理步骤
5 结果分析



5.1 星象信噪比
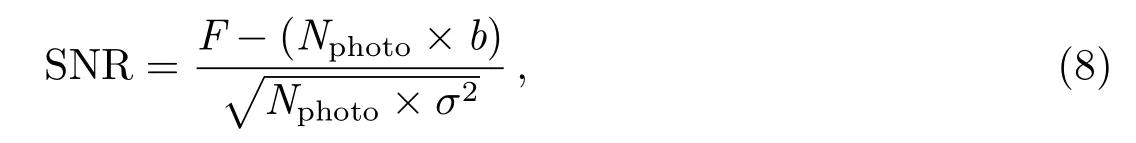


5.2 对暗星的探测能力


6 总结
