景观空间开敞度的量化
2019-02-23张成明
空间的开敞与封闭,不仅是建筑和规划关注的内容,也是风景园林关注的内容。因为对空间开敞与封闭的把握直接关乎环境的品质。
多数文献对空间的研究停留在定性层面,如开放空间、半开放空间、封闭空间和私密空间等。少数学者做了一些建筑空间的定量研究,影响较大的是日本学者芦原义信提出的“D/H”指标,即采用观察点与建筑物之间距离(D)与建筑自身高度(H)的比值作为衡量指标[1]。其指标就是对空间开敞度的研究,简单易懂,但其关注的是明确的建筑空间,很难应用于复杂的园林景观空间。钮心毅、徐方对建成环境空间的开敞度做了定量评价研究[2];叶麟对居住小区景观环境做了量化研究[3]。但这些研究均存在不适用于景观环境,或者分析不够全面等问题。
1 视野分析
空间开敞度(spatial openness)就是对空间开敞性的量化,它与人的视野或视力密切相关。空间的开敞与封闭是人的视觉感知,视觉感知的范围(视野)呈横放的、稍扁的圆锥体状,眼睛为圆锥的顶部,圆锥的底部水平方向略宽。站立不动时,双眼的视野是水平方向120°,垂直方向70°[4-5]。
考虑到仰视时,眼睛的角度并不是固定的,所以仰视视角取120°。这样,景观空间基本上可以看作是由1个视野锥体和1个内凹的环视环所组成(图1)。
2 空间开敞度的量化指标
空间开敞度(以下简称“开敞度”)用来描述建筑外部空间的开敞程度。开敞度的量化指标主要有视野空隙率、遮挡物距离、遮挡物高度和视野权重等。
2.1 视野空隙率
视野空隙率是指在垂直于视轴线的视野面中,“空”的面积与视野面面积之比。在这里,“空”的内涵不仅包括天空,还包括没有被遮挡的“空”的地面。视野面实际上为椭圆状,但在做开敞度分析时,一般设定为矩形或者圆形。
2.2 遮挡物距离
空间的开敞与否不仅涉及某个界面围合的小空间(如一个亭子下的空间),还要考虑这个小空间外的空间,这样才能整体地理解这个小空间。那么对于小空间,需要考虑多大的外部空间?
在城市空间中,人们一般认为城市广场是开放的。通过对欧洲大量中世纪广场尺寸的调查和视觉测试得出:距离一旦超出110m,肉眼就无法辨认出远处的人,这个尺寸就是广场尺寸,即超过110m之后才能产生广阔的感觉[6]。因此,笔者以110m作为研究开敞空间的尺度。
距离越远,遮挡物对空间的限定就越弱。当距离达到110m时,遮挡物的限定效能可以被认为是0,空间100%开敞。所以,可以设此时遮挡物的开敞系数为1;当距离为0时,遮挡物的开敞系数为0。图2为不同距离的开敞系数,公式为:

式中,K距为距离开敞系数;D为物体与观察者的距离。特殊情况下,当D≥110m时,K距=1。
2.3 遮挡物高度
遮挡物的遮挡效能与视点的高低(视高)有关,或者说与视平线有关。遮挡物在视平线以上则为有效遮挡,视平线以下,随着遮挡物高度的降低,效能减弱。视高的差异其实是身高的差异,而身高会因为年龄、性别和地区等差异而不同。成人与儿童对空间开敞度的感知有很大不同,中国人与外国人的空间感知也不相同,本文探讨的是中国人平均视高基础上的空间感知。
2.3.1 平均视高
根据《中国居民营养与慢性病状况报告》,2012年我国18岁及以上成年男性平均身高167.1cm,女性155.8cm[7]。人的头长一般为身高的1/7[8],眼睛一般在头的中间位置,所以,视高=身高-(身高x1/7x1/2),由此推算出我国男女的平均视高分别为153.0和144.7cm。为便于研究,视高取150.0cm。
2.3.2 高度开敞系数
在环视中,如果物体的高度在视平线以上,那么这个物体就是遮挡物体,就具有了100%的遮挡效应。低于视平线的物体的遮挡功能会随着高度的降低而减小,当高度降至0.6m以下时就可忽略不计[9]。提出“高度开敞系数”这一概念,当物体的高度达到1.5m及以上时,其高度开敞系数为0;当高度降至0.6m及以下时为1;当物体高度在0.6~1.5m之间时,高度开敞系数与高度呈线性关系(图3),公式为:
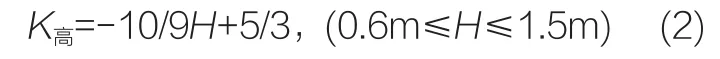
式中,K高为高度开敞系数;H为物体高度。特殊情况下,当H≤0.6m时,K高=1;当H≥1.5m时,K高=0。
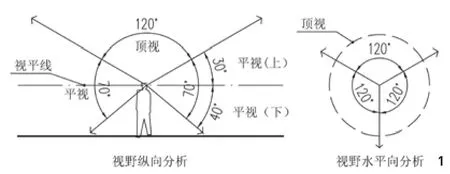
图1 视野纵向与横向分析
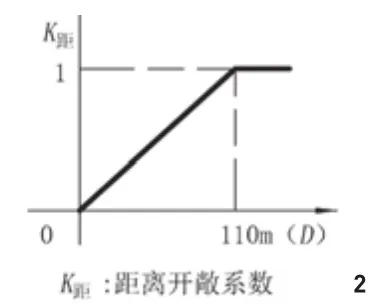
图2 不同距离的开敞系数
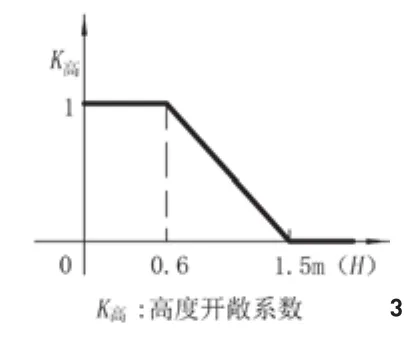
图3 不同高度的开敞系数

图4 仰视与环视开敞度权重分析
视点的平面位置也会影响人对空间开敞度的感知,在场地中心与边缘的感知结果是不同的。为便于分析,笔者假定视点的位置(平面上就是人的位置)在场地中心,因为这个位置所感知的空间最为全面。另外,如果广场中有个亭子,那么在亭子内外所感知的空间开敞度也是不同的,亭子外的开敞度较大。
2.4 视野权重
从上文得知,一般情况下,空间开敞度涉及环视和仰视,当然,有时会涉及俯视。根据视野体量的占比来确定环视和仰视的权重。
在地面上,同等清晰度的整个视野近似半球形,从上到下由两部分组成:仰视椎体和环视环。环视环又分为视平线上的部分和视平线下的部分。从图4中可以看出视平线下的部分所占份额极小,因此可以粗略地认为环视环就是视平线上的环视环。
设V仰、V环分别表示仰视视野、环视视野,R为视野的半径,由此可推算出V仰=1/3πR3,V环=V半球-V仰=1/3πR3, 所以,V环=V仰,因此:

式中,O总为空间开敞度;O环为环视平均开敞度;O顶为仰视开敞度。
3 简单景观空间的开敞度
简单景观空间指的是平面为正方形、被周边遮挡物(如建筑)围合形成的空间,空间内没有树木。
3.1 环视开敞度公式
根据上文所述,可以得出环视开敞度公式为:

式中,O环为空间开敞度;S空、S地、S视分别为视野图面中天空、地面、整个视野的面积;k距、k高分别为距离和高度开敞系数。
“S遮k距(1+k高)”可以理解为增加的天空或地面的面积。如果遮挡物高于1.5m,公式(4)可以简化为:O环=(S空+S地+S遮D/110)/S视×100%(D为观察者与遮挡物的距离)。
3.2 仰视开敞度公式
空间的开敞度不仅与环视有关,还与仰视有关,仰视开敞度计算如下:

式中,O仰为顶面开敞度;S空、S遮、S视分别为仰视视野水平截面中,天空、遮挡物、整个视野截面的面积。仰视视野水平截面可以按照矩形或者圆形来设定。
下面以D/H=4的简单空间来说明公式的应用(图5、6)。
对于这个简单的方形空间,一个方向的环视开敞度就是整个空间的环视开敞度。如图6所示,一个方向的环视开敞度首先就是“空”的部分所占的比例,在图中就是天空(矩形dcef)和地面(矩形aghb)所占的比例,就是(Sdcef+Saghb)/Sghef。其次,开敞度还必须考虑遮挡物(矩形abcd)与观察者的距离。随着距离的增加,遮挡物的遮挡效能减弱,或者说减少的部分就等于增加的天空的面积。这部分增加的面积就是S空增。S空增=S遮k距(1+k高)。
由于遮挡物的高度超过了1.5m,根据公式(2)和图3,k高=0;根据公式(1),k距=12/110。
根据公式(4),O环=[S空+S地+S遮k距(1+k高)]/S视×100%=(S空+S地+S遮×12/110)/S视]=[(Scdfe+Sabhg+Sabcd×12/110)/Sghef]=[2.428+8.569+6×12/110]/16.997=68.6%。
由于仰视中没有遮挡物,所以O仰=100%。根据公式(3),O总=(O环+O仰)/2×100%=([68.6%+100%)/2]=84%。即在观察点,该空间的开敞度为84%。
3.3 不同D/H值的空间开敞度
遮挡物(如建筑、植物等)距离与遮挡物高度比“D/H”值的大小,影响空间的开敞度。根据前文的公式,可以计算出D/H变化时,不同高度遮挡物围合的空间的开敞度。图7为围合建筑高度为6m时的剖面图,D/H值分别为1、2、3、4、6、10。表1是不同D/H值和各种高度遮挡物的空间开敞度。
从表1中可以发现以下规律:
2)D/H=1时,空间开敞度的变化最大;
3)D/H=3时,建筑间距在24m以内,开敞度比较稳定,空间开放但仍不失围合感;
4)D/H≥4时,不论建筑间距多大,空间已经非常开敞。
D/H恒定时,开敞度与遮挡物高度成一定函数关系,函数方程表示的回归曲线或回归直线如图8所示,回归线方程如下:
D/H=1时,y=-6×10-11x6+4×10-8x5-8×10-6x4+0.000 9x3-0.051 8x2+1.882 7x+15.38,(R2=0.996 4)①
式中,y为开敞度,x为遮挡物高度,下同。
D/H=2时,y=3×10-9x6-10-6x5+0.000 2x4-0.011 8x3+0.404 1x2-5.761 6x+79.026,(R2=0.985 8);
D/H=3时,y=-3×10-6x4+0.000 3x3-0.005 3x2+0.157 2x+76.926,(R2=0.9973);
第二阶段:当阴极侧含水量上升至饱和状态时,继续产生的水就会在阴极侧结冰堆积。同时,化学反应放出的热提高电池温度。如果电池温度在阴极侧催化剂层全部被冰覆盖之前仍低于0℃,燃料电池就会停止运行,此时冷启动失败。反之,冰会在融化过程中吸收热量,保证电池温度在0℃左右[14]。
D/H=4时,y=0.000 1x4-0.007 7x3+0.185 2x2-1.222 2x+91.2,(R2=1);
D/H=6时,y=0.333 3x+82,(R2=1);
D/H=10时,y=0.055 6x2-0.5x+95,(R2=1)。
4 较复杂的景观空间开敞度
以一个亭子为例。开敞的空间有了亭子,头顶上有了庇护,便立刻有了室内的感觉。如果顶部封闭、面积较大、高度较低,那么室内的感觉会更加强烈,这时,亭子内的开敞度大大降低。下面讨论在D/H=4的简单空间内,不同高度时亭子内空间的开敞度(图9)。

图5 简单空间平面与剖面
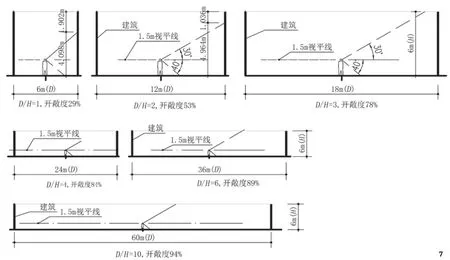
图6 环视一个方向的透视图(水平视角90o)
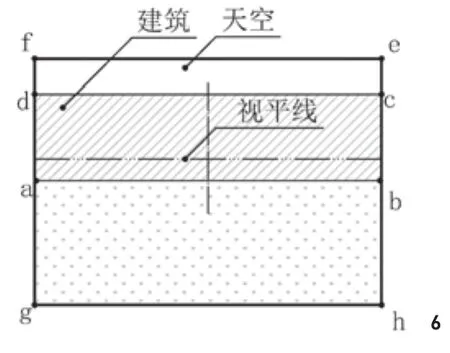
图7 建筑高度6m时,不同D/H值的户外空间开敞度
假定条件:1)亭子的净高度有3种,分别为2.5、3.5和4.5m;2)亭子屋面大小为4mx4m,为密实不透明结构;3)亭子为伞状结构,周边没有柱子等围合物体。
从前文可知,在没有亭子的情况下,空间的开敞度为84%(图7)。
根据公式(5),2.5m顶棚的仰视开敞度为:

由于顶棚全部遮挡了视线,所以S遮=S视,O仰=D/110=1/110=1%。由于亭子没有柱子,亭子里的环视开敞度就是没有亭子时的环视开敞度,即84%。
根据公式(3),O总=(O环+O顶)/2×100%=(84%+1%)/2=43%。即亭子里的总开敞度为43%。由此同样可以算出顶棚高度3.5和4.5m时的开敞度。
顶棚高度3.5m时:
O仰=(S空+S遮×D/110)/S视×100%=(14.2+16×2/110)/30.2=48.0%
O总=(O环+O顶)/2×100%=(85%+48%)/2=66%
顶棚高度4.5m时:
O仰=(S空+S遮×D/110)/S视×100%=(57.3+16×2/110)/73.3=78.6%
O总=(O环+O顶)/2×100%= (85%+79%)/2=82%
表2为不同高度亭子的开敞度,总开敞度与实际的感受情况一致。当然,有柱子时或者顶棚较大时开敞度会略有降低,因为环视视野和仰视视野会受到较多遮挡。
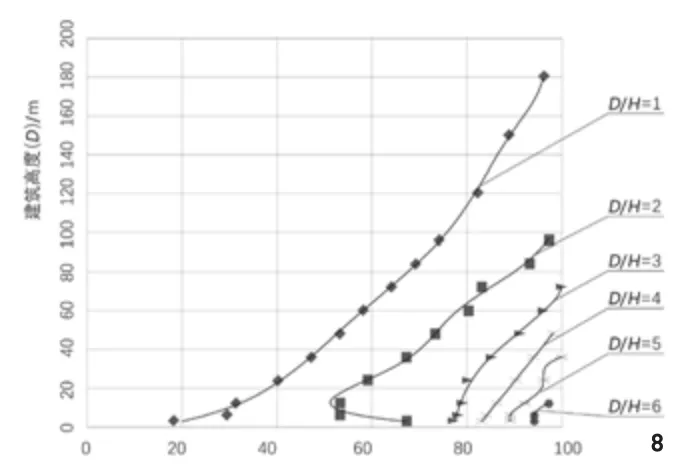
图8 D/H、建筑高度与开敞度关系
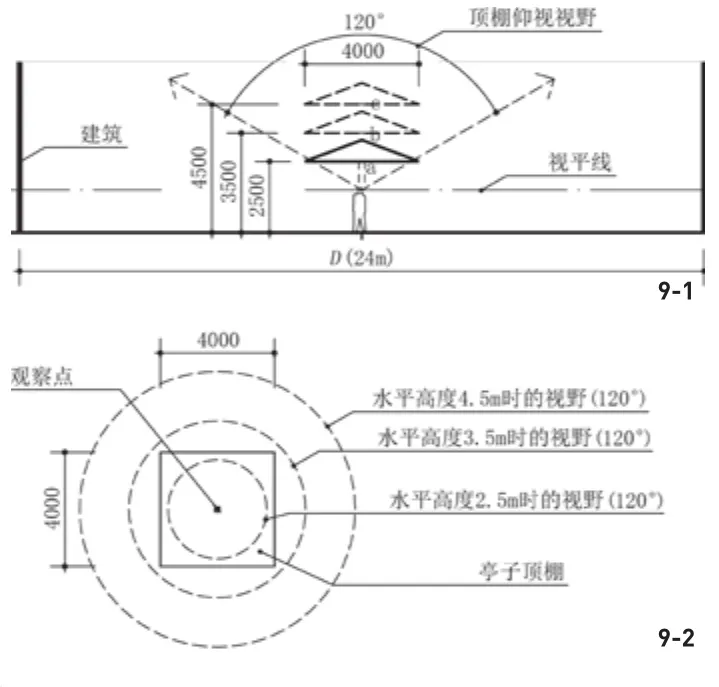
图9 亭子剖面(9-1)与平面(9-2)
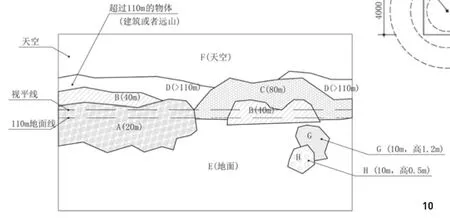
图10 复杂的景观空间开敞度计算
5 复杂的景观空间开敞度
复杂景观空间遮挡物的距离和高度各有不同,而且由于叶子的多孔性,植物的遮挡常常不是全部遮挡,但是空间的量化仍然可以运用上文的公式。
在公式(4)中,S遮k距(1+k高)最为复杂,随着视野内遮挡物的增多,S遮的计算量也在增加,可以将S遮k距(1+k高)表达为新增加的“空”,就如同天空和地面的“空”一样,公式为:
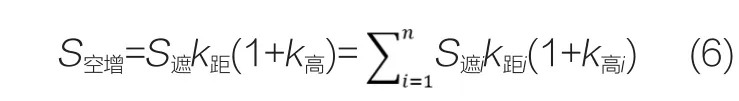

下面以一个景观场景来说明该公式的应用。图10是上文分析的一个环视场景,观察者顶部没有物体,垂直视角为70°,其中水平线上视角30°,下视角40°,水平视角90~120°,近似于单反相机的广角镜头。
首先,根据距离划分出不同的块,分块不宜过多,否则计算难度增大。遮挡物G在视平线下,超过了0.6m,要纳入计算中;遮挡物H低于0.6m,忽略不计。
根据公式(4),O环=[S空+S地+S遮k距(1+k高)]/S视×100%,在CAD中计算的结果是O环=82%。计算的难点是利用公式中的“S遮k距(1+k高)”,因为需要计算每一块遮挡物(除H之外)。同样可以计算出整个环视的其他方向的环视开敞度。假定,其他方向的环视开敞度分别为:80%、76%、90%,那么整个环视的开敞度就是(82%+80%+76%+90%)/4=82%。根据公式(3),O总=(O环+O顶)/2=(82%+100%)=91%,即该场景的空间开敞度为91%。

表1 D/H、建筑高度与开敞度

表2 不同高度亭子的开敞度
6 特殊景观空间的开敞度
以上探讨的空间都以地面平坦为前提(图11a),实际上,景观空间是多样的。特殊景观空间包括洼地和高地(图11b、c),所体现的开敞度要比平地大,那么如何量化这些特殊的空间?
假定地面以下不存在,人们看到的世界就像跳伞运动员从空中看到的一样。如果在以观察点为圆心,以110m为半径的球状范围内没有遮挡物,那么这个空间的开敞度就是200%。当然,也可以把这样的空间定义为开敞度100%,似乎更加科学,但是这样的话,草原的空间开敞度就是50%,这和我们的常识不符。一般认为,一望无际的草原就是开敞空间,就是100%的开敞空间。所以,本文开敞度的设定考虑了常识,毕竟开敞度100%以上的空间不常见。
由于地平线以下的视野近似于视平线下的半球视野(半径110m),所以地平面以下的空间开敞度为:
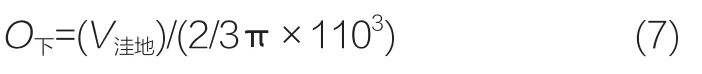
式中,O下为地平面以下的开敞度;V洼地为地平面下被感知的空的部分,如图12中的阴影部分。
下面进行高地上开敞度的计算。图12是穿过观察点的垂直剖面,高地高25m,图中阴影区为地平面(或称脚平面)以下的可见视野,半径在110m范围内。根据左右2块阴影可以粗略地计算出视野体积。当然,增加剖面会使计算结果更加精确。根据公式(7),计算出的结果是地平面以下的开敞度为19%。如果以观察点为圆心,环视和仰视110m的范围内没有遮挡物,那么该观察点的空间开敞度就是119%。
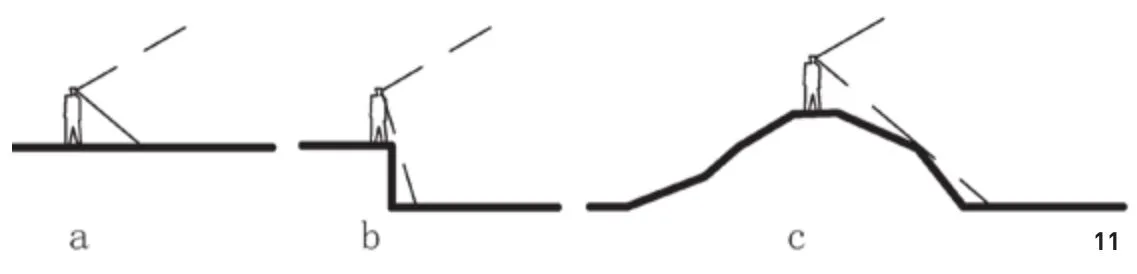
图11 特殊景观空间示意

图12 山地景观空间开敞度的计算

图13 亭子里各个方向的开敞度
7 实景开敞度量化步骤
实景是指已经存在的景观空间,计算实景开敞度的步骤如下。
1)拍摄。可以用带广角的相机拍摄观察点的各个角度,须至少4个角度,仰视1个、环视3个,环视拍4~8张均可。在环视拍摄中,尽量保证视平线上视角30°,下视角40°,或者保证视平线在画面中偏上的位置。
2)导入CAD。将图片导入CAD,以便量取数值。
3)分块。根据不同的遮挡物距离分块,不宜过多。测量“块”的面积,并实测或估算“块”与观察者的平均距离。
4)计算。开敞度的计算涉及仰视、不同角度的环视和俯视等,应用上文中的7个公式进行计算。
以图13的公园实景为例,以亭子中的视角来分析公园的开敞度。先在亭子中拍摄各个角度的照片,然后按照步骤计算仰视以及各个环视空间的开敞度。
O总=(O环+O顶)/2×100%=[(0.83+0.92+0.78+0.89)/4+0.2]/2=43%。
因此,亭子中的总体开敞度是43%。
8 结语
此次景观空间的量化研究将观察者所在的整个空间统一了起来,包括环视、仰视和俯视。提出景观空间量化的4个指标:视野空隙率、遮挡物距离、遮挡物高度和视野权重。景观空间的量化将会使我们对景观空间的认识由感性层面上升到理性层面,便于更加深入细致地理解和应用各种开敞度的景观空间。
本文关于景观空间开敞度的研究是建立在距离观察者110m范围内的空间,更大空间开敞度的研究还需要进一步深入探讨。
注释:
①R2值越接近1,其拟合效果越好。
注:文中图片均由作者绘制或拍摄。
