基于贝叶斯理论道路拥堵预测的最短路问题研究

文/苗军 南京财经大学管理科学与工程学院 江苏南京 210023

1、引言

近年来交通网络优化已经成为交通问题研究的热点。而城市交通网络的最短路问题的分析可以有效地缓解资源的配置问题，也越来越成为热点问题，对现实生活中的城市道路进行最短路分析，首先要将现实的城市道路网络抽象化为图论中的网络图，在确定网络图相应的权重后按照适当的算法及软件进行最短路分析，从而得到最短路问题的解。

在交通网络中，最短路分析一般是指网络图中各路段的权值之和最小，这个权值可以是出行的时间，也可以是出行的费用。而对于权值不同的理解，又可将此类问题分为两大类：一是将权值看作是非随机变量，当这个非随机变量不随着时间的变化时就是确定性静态最短路，反之，如果随着时间的变化而变化，那就是确定性的动态最短路问题。第二大类则是将权值看成是随机变量，每个不同值的出现是有一定的概率的，此时在求最短路的时候就要转换成求期望值最小。

在道路拥堵预测最短路问题的研究中，关于将权值看作是随机变量所涉及的相关理论，前人已经做了很多工作：Miller-Hooks E（2003）[1]把交通网络图中各个路段上的路权看作是一个与时间相关的随机变量，将各个期望值的赋为路段的权值，进而求得起始点到终点的最短路。袁二明等（2013）[2]通过对交通拥堵的预测来修正交通网络中发生拥堵的概率分布，从而得到在交通网络期望费用值最少的最短路线，算例仿真结果表明交通拥堵预测能起到积极作用。此外，谈蔚欣（2006）[3]介绍了样本数据处理的具体过程，确定了合适的拥堵预测指标体系，选择了LMBP神经网络作为组合分类器的元学习算法，选用了投票法和平均法作为分类器输出的组合规则。并针对整个拥堵预测过程做了系统的阐述。

而在求解道路交通的最短路的相关算法与理论上：黄国浪（2014）[4]提出了一种新的城市交通拥堵识别算法，并对城市交通拥堵预测中的关键技术交通流参数短时预测进行了深入研究，建立了一种多模型融合预测方法。陈允峰（2015）[5]提出了两种利用Lingo软件求解的最短路方法，并给出具体的实例验证了其中的正确性。邹桂芳和张培爱（2011）[6]在Gauss-Seidel迭代法思想的基础上，提出了一种改进的Floyd算法来计算任意两点之间的最短路问题。丁浩和苌道方（2014）[7]利用Dijkstra算法来迅速寻找出快递车辆配送派件过程中的最短路，并与解决该类问题常用的遗传算法，蚁群算法进行了比较分析。

2、模型与建立与求解

本文所研究的问题是城市道路交通拥堵问题，由于道路是否拥堵是一个不确定性的因素，具有一定的概率值，而且拥堵以及不拥堵所消耗的费用（考虑到信息成本的单位，这里统一使用费用而不是时间）也是有所不同的，所以本文所建立的网络图问题是属于第二大类别---将权值看作是随机变量，在此，关于如何确定拥堵的概率值以及所花费的时间来计算期望值（权值）就显得至关重要了，本文假设驾驶员根据自己的以往经验，大概预估出所选择的道路的拥堵的概率值。即拥堵与不拥堵的可能性。当然，驾驶员也可以在了解交通预测的结果和以往的信息的基础上，对原有的道路拥堵的可能性做出修正，修正所涉及的原理就是贝叶斯定理。下面则是建模的具体步骤：

第一步：驾驶员根据经验对网络图的各个路段的拥堵情况做出的预估，A1表示路段发生拥堵，A2则表示不发生拥堵，其对应的概率值就用P（A1）与P（A2）来表示，这个概率值成为先验概率，根据先验概率以及费用可以得出每个路段相应的期望值，进而得到最优选择的状况下的期望值。

对于任意一路段，设其在拥堵时的费用记为F1，在不拥堵的状况下的费用是F2，则其在路段中的期望值是：

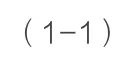
由上述的公式的到了各个路段的出行费用的期望值，将该期望值设为权值，利用Lingo软件可以求解相应的最优解，即最小的总期望值ETOTLE，同时也能得到相应的最优交通路线。

第二步：由于上一步获得的信息不完全准确，我们要对先验概率进行修正，这就用到了贝叶斯公式来对上述的概率进行进一步的修正：

此时利用上式得到的期望值就是：

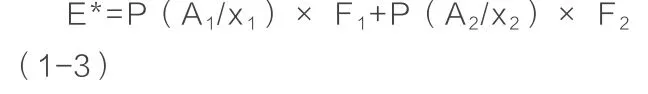
这样就得到了修正后的出行费用的期望值，同样以E＊代替E得到新的权值，利用Lingo得出最优的路径和最小的总期望值E＊TOTLE 。

第三步：在上面两个步骤的基础上，本文可以用情报价值来判断是否应该做出预测，即：

其中C表示获得以往的预测信息所耗费的成本，当EVPI＞0的时候，说明预测所带来的收益是大于不预测带来的收益的，我们认为预测是有用的，反之，如果EVIS≤0的时候，就没有必要进行预测了，因为这时候的预测成本超过了预测所带来的收益。

3、算例仿真

图1 某区域道路的网络图

简单地将某个地区的道路交通路线抽象为上述的交通网络图。每个路段的拥堵情况以及相应的费用如表1所示：

上表中的每个路段的权值E可由公式（1-1）计算出来，这样就得到了初步的权值矩阵。

利用Lingo软件得到图2所示的结果：

图2 最短路线问题的运行结果

上述的结果表明最小的期望值是18，由X（1，3） X（3，6）取值为1，其他的取值为0可以推出该路线：为1→3→6。

此时，通过表1观察到1-3和2-3的路段的拥堵概率是最大的（为0。6），即最有可能发生拥堵，不妨以1-3路段为例，下一步要进行的是利用贝叶斯公式来计算一下修正概率。

表2 对于1-3路段预测拥堵情况的准确度

由贝叶斯全概率公式，可以得出1-2路段中的预测拥堵以及不拥堵的概率：

可以求得，1-3路段中预测拥堵且实际就是拥堵的概率为：

同理可知其他的情况，如下表所示：

表3 拥堵情况修正后的概率值

这里我们就可以对1--3路段重新赋予新的权值（期望费用）：

当该路段预测拥堵时，其期望的费用值为 E1-3= P（A1/x1）× F1+P（A2/x1）×F2=0.567×10+0.433×8=9.134，此时在计算最小的总期望费用时，只需要将1-3路段的权值从9.2改为9.134即可，这样就得到了最优的总期望费用：17.934；相应的路线依然不变，还是1→3→6。

而该路段预测不拥堵的时候，E1-3= P（A1/x2）× F1+P（A1/x2）× F2=9。286，此时交通网络的最优的期望费用为18.086；对应的最优路线也是依然没有变化。

由上述的公式可知E＊=17.934×0.74+18.0 86×0.26=17.973

因此，当进行预测的成本C大于18-17.973=0.026时，收集信息的成本是大于进行预测的所节约的费用，此时可以选择放弃预测，否则，可以进行预测。

结论：

本文用修正的概率公式对网络图的路线进行改进，结果表明，在收集信息的成本超过0.026的时候，情报价值小于收集信息所需要的成本，预测反而不如不预测。而当收集信息的成本小于0.026时，则可以进行预测分析以获取更大的利益。本文通过贝叶斯预测以及信息的价值与成本之间的关系，对是否进行预测做出了完整的解释，当然，本文也有许多不足之处：一是在改变权值时，最小的总期望费用是随之改变的，而最优的路线也是可以变化的，这里并没有考虑在内；二是没有考虑到实际路况的复杂程度，比如说红绿灯、驾驶员的移动偏好等因素，而只是利用最简单的网络图来抽象实际的情况，这将是以后研究的重要方向。