考虑流固耦合的拱坝抗滑稳定非概率可靠度分析

王晓玲，刘明辉，石祖智，朱晓斌，王 振，吕明明



考虑流固耦合的拱坝抗滑稳定非概率可靠度分析

王晓玲，刘明辉，石祖智，朱晓斌，王 振，吕明明

(天津大学水利工程仿真与安全国家重点实验室，天津 300350)

拱坝抗滑稳定可靠度分析是大坝安全评价的关键组成部分，其结果直接关系到大坝正常运行与安全，具有重要研究意义．已有的研究多采用概率可靠度方法进行分析，然而实际拱坝工程统计信息较少，难以获得各参数变量的精确概率分布；另外，目前缺乏考虑坝基岩体流固耦合作用的拱坝抗滑稳定可靠度研究．针对上述问题，基于凸模型理论，提出了考虑流固耦合作用下的拱坝三维抗滑稳定非概率可靠度分析方法，并通过建立拱坝三维工程地质统一模型，分别采用超载法与强度折减法，对流固耦合作用下拱坝抗滑稳定非概率可靠度进行探究．实际工程应用表明：本研究能够在缺乏足够统计信息的情况下对拱坝抗滑稳定可靠度进行分析，同时，未考虑流固耦合作用将高估拱坝的抗滑稳定可靠度，对工程安全不利．

拱坝；抗滑稳定；流固耦合；非概率可靠度；有限元法

拱坝具有复杂的三维超静定结构，关于其破坏模式、失效机理及安全评价的研究一直是工程界关注的焦点和难点，其常见的失稳方式为坝肩岩体在拱端推力作用下发生的滑动失稳[1]．目前，常用的拱坝抗滑稳定性分析方法有刚体极限平衡法、地质力学模型试验法、有限差分法和有限元法等[2-6]．抗滑稳定可靠度分析将为大坝安全稳定运行提供理论保障．

现有拱坝可靠度分析多采用概率可靠度分析方法，然而由于拱坝结构材料特性、边界条件、系统误差存在诸多不确定性[7]，实际工程中难以获取足够的统计信息以得到各参数变量的精确概率分布，同时概率可靠度分析方法对于概率分布函数十分敏感，不精确的分布函数可能导致最终可靠度分析结果的偏差较大．为解决这一问题，Ben-Haim等[8]和Elishakoff等[9]提出了基于凸模型理论的非概率可靠度分析方法作为概率可靠度分析方法的有益补充，该方法以不确定性参数的变化范围描述参数分布[10-11]，可以利用贫数据得到满足精度要求的分析结果，因此能够适用于考虑参数不确定性的拱坝抗滑稳定可靠度分析．同时，在进行水利工程结构可靠度分析的过程中，渗流场与应力场的耦合作用不容忽视[12-16]．自1959年法国Malpasset拱坝失事后，拱坝坝基的流固耦合问题逐渐得到重视．林鹏等[17]研究分析了坝基流固耦合作用机制，通过三维有限元数值分析，探究了流固耦合作用对拱坝工程结构应力应变的影响；王瑞等[18]通过建立拱坝流固耦合三维有限元模型对流固耦合作用下拱坝的应力场、位移场和渗流场进行了分析；薛娈鸾[19]研究分析了小湾拱坝含排水孔的裂隙岩体坝基中流固耦合作用，并提出复合单元算法．由此可见，现有的研究多是立足于坝基流固耦合作用下坝体应力应变和渗流场的分析，而缺乏对考虑该作用下拱坝抗滑稳定可靠度的研究．综上所述，对缺乏足够统计信息的实际工程条件下考虑坝基流固耦合作用的拱坝抗滑稳定可靠度进行深入探究是十分必要的．

本文基于凸模型理论，提出了考虑流固耦合作用下的拱坝三维抗滑稳定非概率可靠度分析方法．依托实际拱坝工程，通过建立基于NURBS-TIN-BRep混合数据结构的拱坝三维工程地质统一模型，分别采用超载法与强度折减法，分析了考虑流固耦合作用下的拱坝抗滑稳定非概率可靠度，为拱坝工程抗滑稳定分析提供了理论依据和技术支撑．

1 非概率可靠度分析模型与方法

1.1 凸集模型

本文采用凸集模型中基于区间矩阵分析的区间凸集模型[20]为

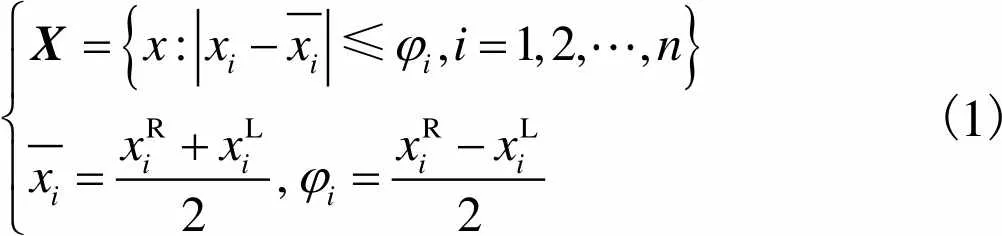
(1)

根据实际工程资料及公式(1)可建立输入变量区间模型，以此对结构参数的诸多不确定性进行考量.

1.2 凸模型的标准化

为了避免由于不同自变量之间量级的差异导致的病态矩阵问题，需要预先对凸集模型中的自变量进行标准化处理，本文采用的标准化处理方法为

(2)

1.3 非概率可靠度指标

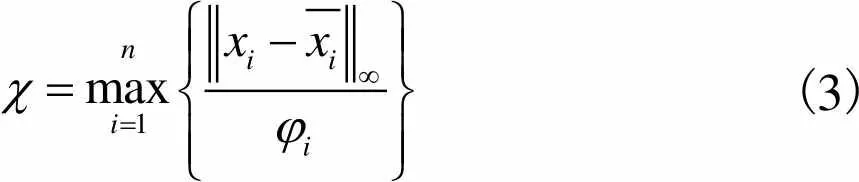
(3)

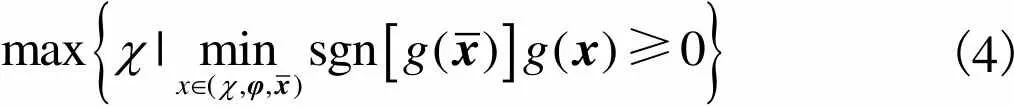
(4)

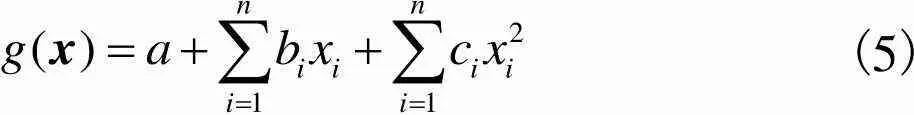
(5)

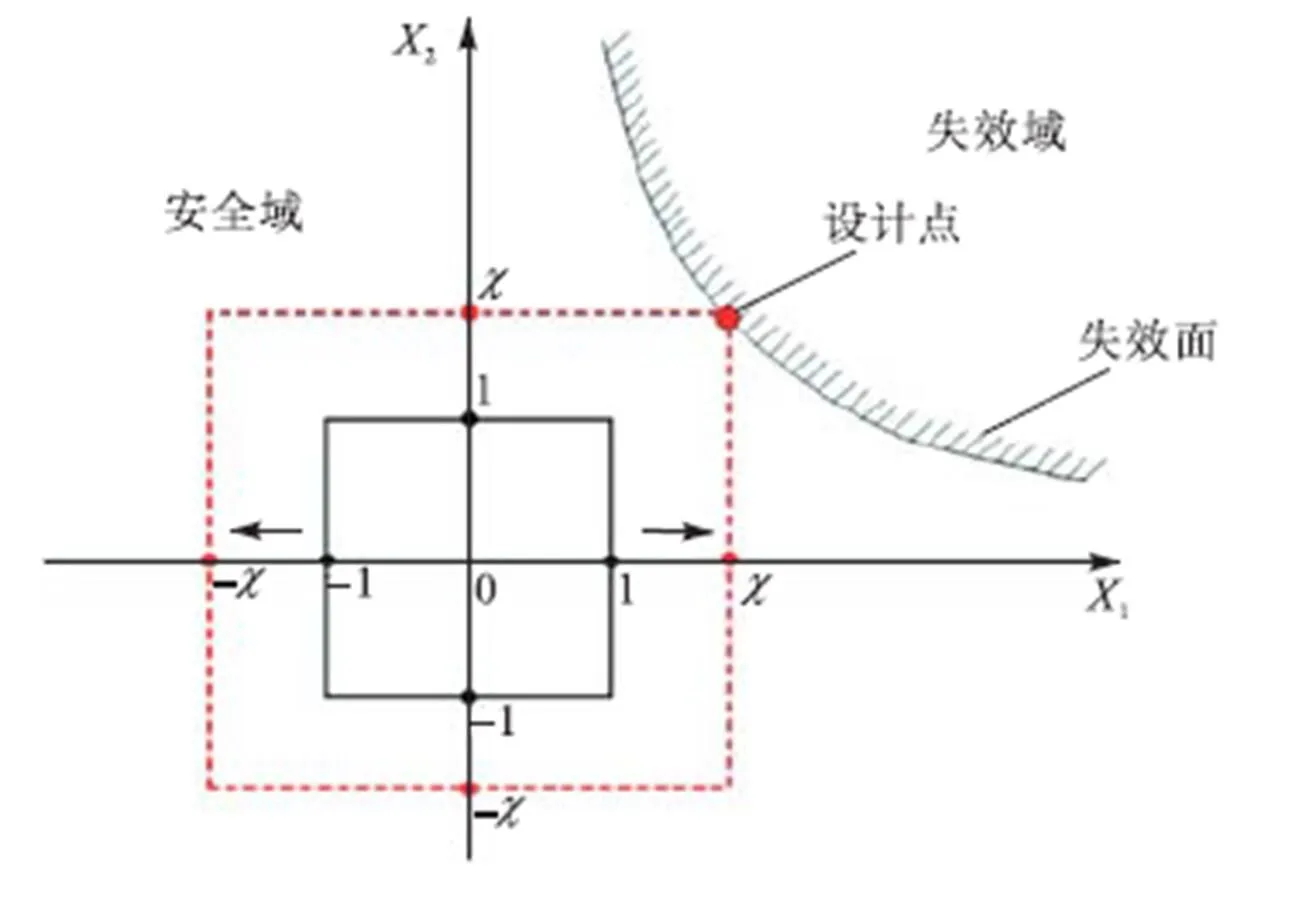
图1 二维模型中非概率可靠度指标

2 流固耦合分析模型与方法

考虑到拱坝工程坝基岩体中同时存在饱和渗流与非饱和渗流，即为有浸润面的岩土体渗流问题，浸润面以下岩土体饱和，浸润面以上岩土体非饱和，因此本文以非饱和土渗流理论为基础研究拱坝坝基岩体的流固耦合性质．

本文基于宏观连续介质原理、有效应力原理、虚功原理以及Forchheimer渗透定律，建立了应力场与渗流场方程，进而组成了流固耦合问题的控制方程组．同时通过对方程组进行耦合求解，得到了耦合后的应力场与渗流场分布．显式化后的平衡方程为

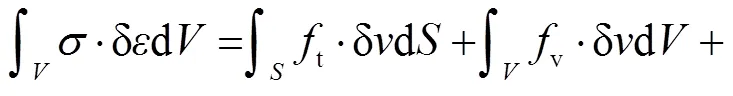
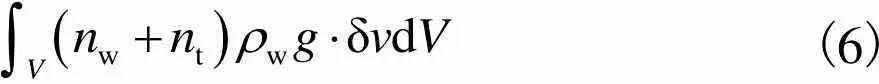
(6)

(7)

(8)

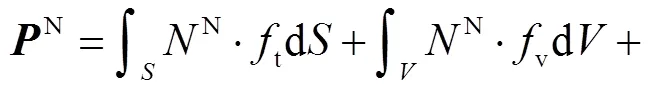
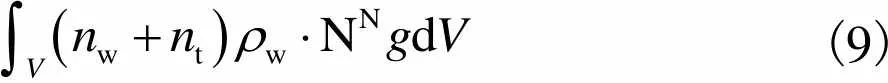
(9)

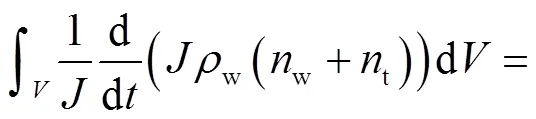
(10)

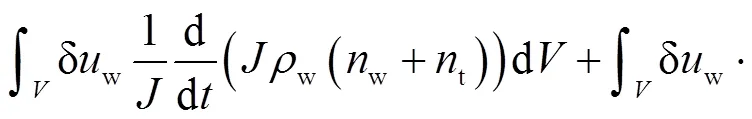
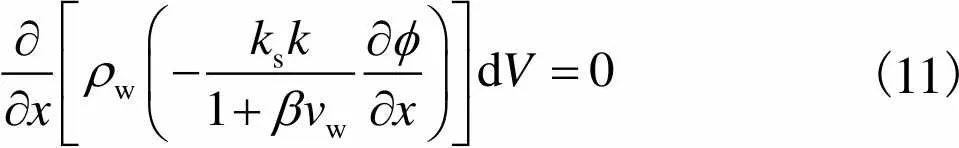
(11)

3 拱坝抗滑稳定可靠度分析

研究选取我国西南地区某高拱坝工程，其挡水建筑物为混凝土双曲拱坝，坝顶高程1135m，正常蓄水位1130m，大坝最低建基面高程925m，最大坝高210m．坝址区河谷呈“Ω”形嵌入河曲形态．两岸基岩裸露，岩体雄厚，谷坡较为陡峻．坝址区河谷为“V”形河谷，狭窄且相互对称．另外山坡坡面发育着一些小沟，但切割较浅，从整体来看，地形较为完整．经过勘测，该拱坝的坝区内存在岩脉断层和裂隙破碎带，但是其引水发电建筑物所处区域并没有区域断裂切割，可以得到坝区岩体的构造型式的特征为有沿脉岩发育的挤压破碎带、节理裂隙以及断层．

3.1 拱坝三维工程地质统一模型建立

本文通过耦合钻孔、剖面、平面地质图等多元数据，基于NURBS-TIN-BRep混合数据结构[23-24]对复杂地质曲面进行插值逼近拟合，建立了拱坝三维工程地质统一模型．假设模型空间研究区域为，其数学模型可定义为

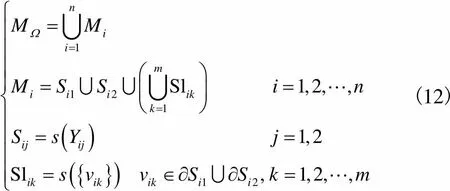
(12)

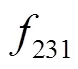
图2 拱坝三维工程地质统一模型

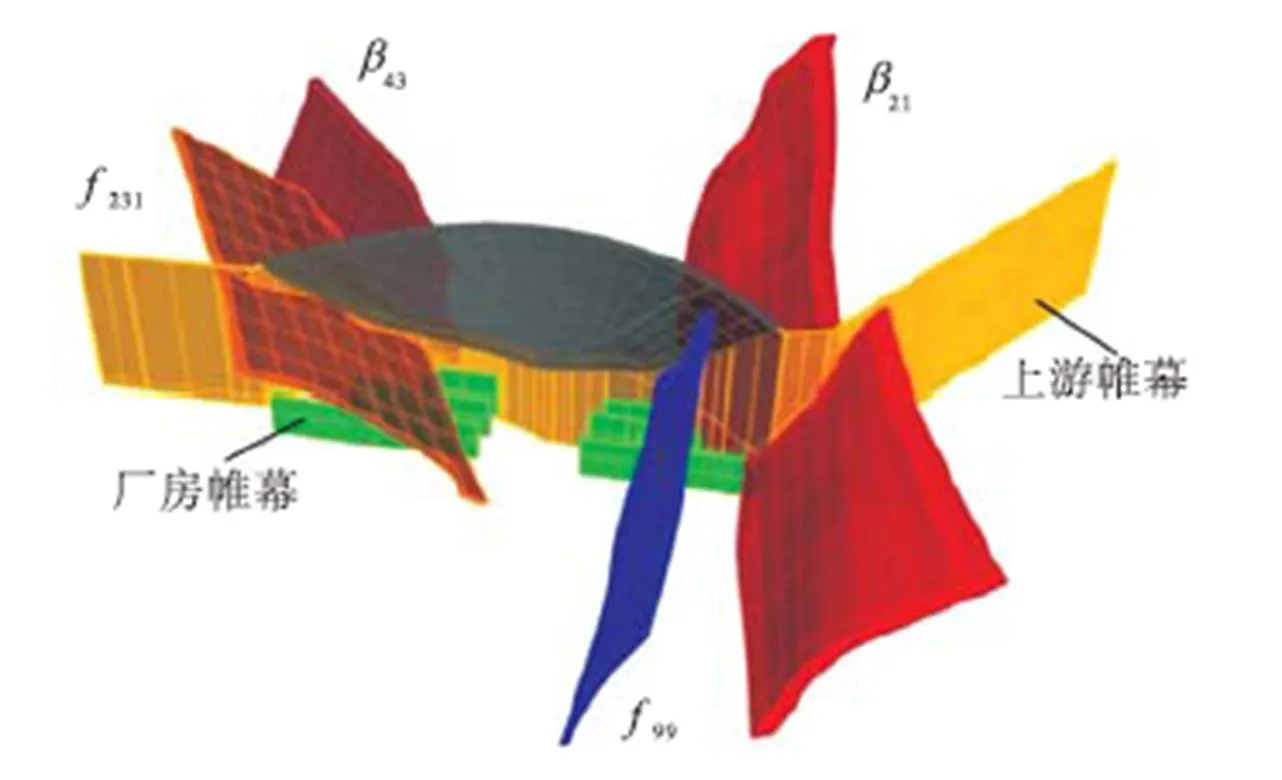
图3 坝基断层、不良地质体与帷幕分布

3.2 拱坝有限元模型建立

本次有限元计算模拟范围为：底面高程为600m，河床高程以下模拟了325m，平面上横河向555m，顺河向1206m．其中包括拱坝中心面以左842m、中心面以右875m的范围，约4倍坝高；且从拱冠梁向上游延伸551m，约2.6倍坝高；向下游延伸842m，约4倍坝高．其固体力学边界为：左、右岸边界面施加向的法向约束，上、下游边界面施加向的法向约束，底面施加向的法向约束．流体力学边界条件为：采用正常蓄水位，坝基四周及底部视作不透水边界，坝体、坝体与坝基之间的接触面、坝基顶面上下游边界采用透水边界，坝基与典型断层、不良地质体、防渗帷幕之间采用透水边界．

通过采用局部网格加密技术，对坝体、防渗帷幕、典型断层及不良地质体附近的网格进行加密，如图4所示．本次计算模型网格共计172237个单元和321596个节点，结构体采用孔压单元进行离散．

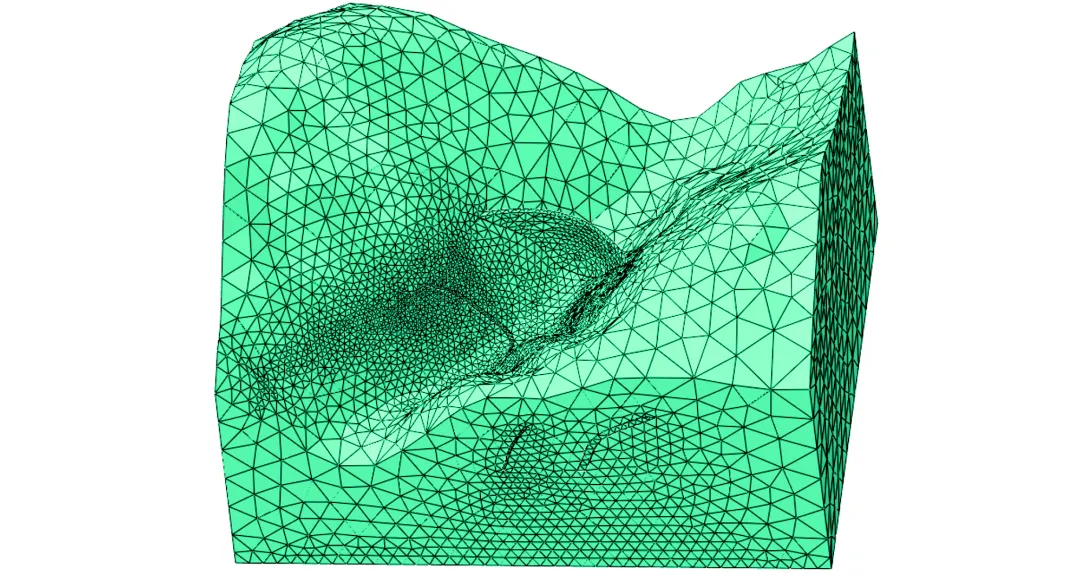
图4 网格模型

3.3 拱坝模型有限元参数选取

该拱坝坝址区河床覆盖层较为浅薄，且坝基岩体岩性较为单一，主要为花岗岩，其中有灰白色以及微红色黑云二长花岗岩分别分布在上坝址和下坝址．本文基于等效连续介质模型，其中混凝土结构采用考虑拉断的Mohr-Coulomb本构模型，其他岩体结构采用Dracker-Prager本构模型进行结构计算．基于凸模型理论与查阅得到的实际工程情况确定上述各地质体结构的力学参数以及荷载的区间变化范围如表1所示，其中高程系统采用以似大地水准面所定义的正常高系统．

为研究考虑流固耦合作用下拱坝的三维抗滑稳定可靠度，本文选取的计算工况为

(1) 坝体自重＋上游正常蓄水位＋相应下游水位＋泥沙压力＋扬压力；

(2) 坝体自重＋上游正常蓄水位＋相应下游水位＋泥沙压力＋扬压力＋渗流(流固耦合)．

表1 结构模型力学与荷载参数

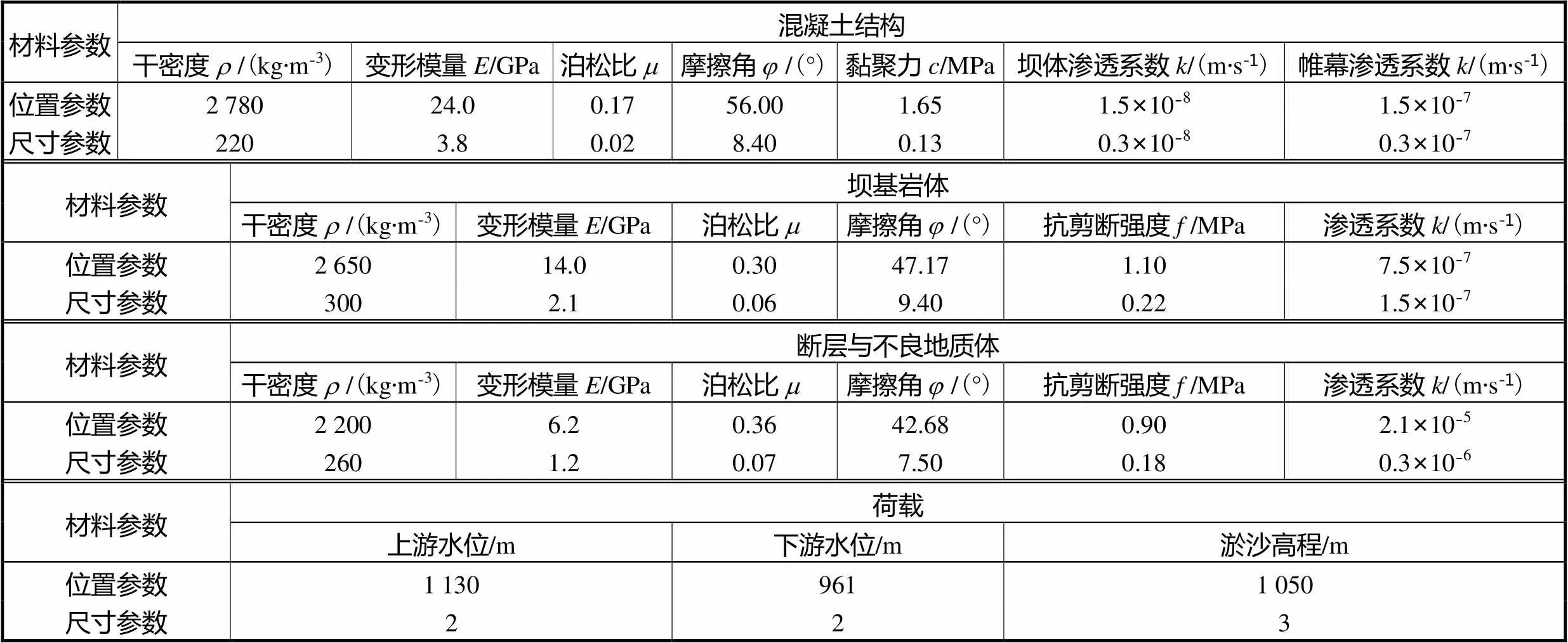
Tab.1 Mechanical parameters and loads of structural model

3.4 结果分析

3.4.1 抗滑稳定安全系数分析

首先，选择位置参数下的拱坝结构进行三维抗滑稳定分析．分别采用超载法与强度折减法对拱坝的抗滑稳定性进行计算，其抗滑可靠度系数通过计算是否收敛、位移是否产生拐点、是否产生塑性区破坏等判别依据[26]进行综合判断．

基于有限元分析对拱坝上游水压力进行超载计算，进而分析结构抗滑稳定性．当超载系数达到5.216时，计算停止收敛，可以得到相应荷载下的等效塑性应变如图5所示，由图5(a)可知，经过基于流固耦合的有限元计算，最先产生滑动失稳的是位于坝后右岸坝肩处的断层213，同时由于超载的施加，坝体产生了剪切破坏，且拱坝通过坝肩传力给软弱地质体，导致其面上产生塑性区，进而坝体失去支撑而破坏；由图5(b)可知，在坝体滑动作用下，建基面也发生部分塑性破坏．另外，通过从拱冠梁和左、右岸坝肩选取共5个特征点对其位移进行分析，可得到如图6所示特征点随超载系数变化的位移曲线，由于是对上游水压力进行倍数超载计算，因此破坏时拱冠梁顶点处最大位移达到66cm，这在正常荷载下是不会出现的，另外可见特征点位移在超载系数为5.0时产生突变，同样说明结构产生失稳．基于判别方法的简便性考虑，选取拱坝超载抗滑安全系数为失敛超载系数5.216．

为了与超载法对比，本文采用强度折减法，通过设置场变量，对拱坝的坝基岩体、断层和不良地质体的摩擦角和抗剪断强度分别进行折减，进而利用有限元法对拱坝结构进行稳定性分析．当强度折减系数达到3.284时，计算停止收敛，其相应的等效塑性应变如图7所示．由图7(a)可知，随着相关岩土体强度参数的折减，仍然是坝后右岸坝肩处的断层213首先发生塑性破坏，同时，随着岩土体强度的折减，坝肩岩体逐渐难以承担外荷载作用，因而坝肩产生一定程度的塑性破坏；如图7(b)所示，建基面在坝体滑动作用下也发生部分塑性破坏．接着对选取的拱坝特征点位移过程进行分析，如图8所示，当强度折减系数为3.0时，特征点位移产生突变，说明结构产生失稳. 因此，可选取拱坝强度折减抗滑安全系数为失敛折减系数3.284．

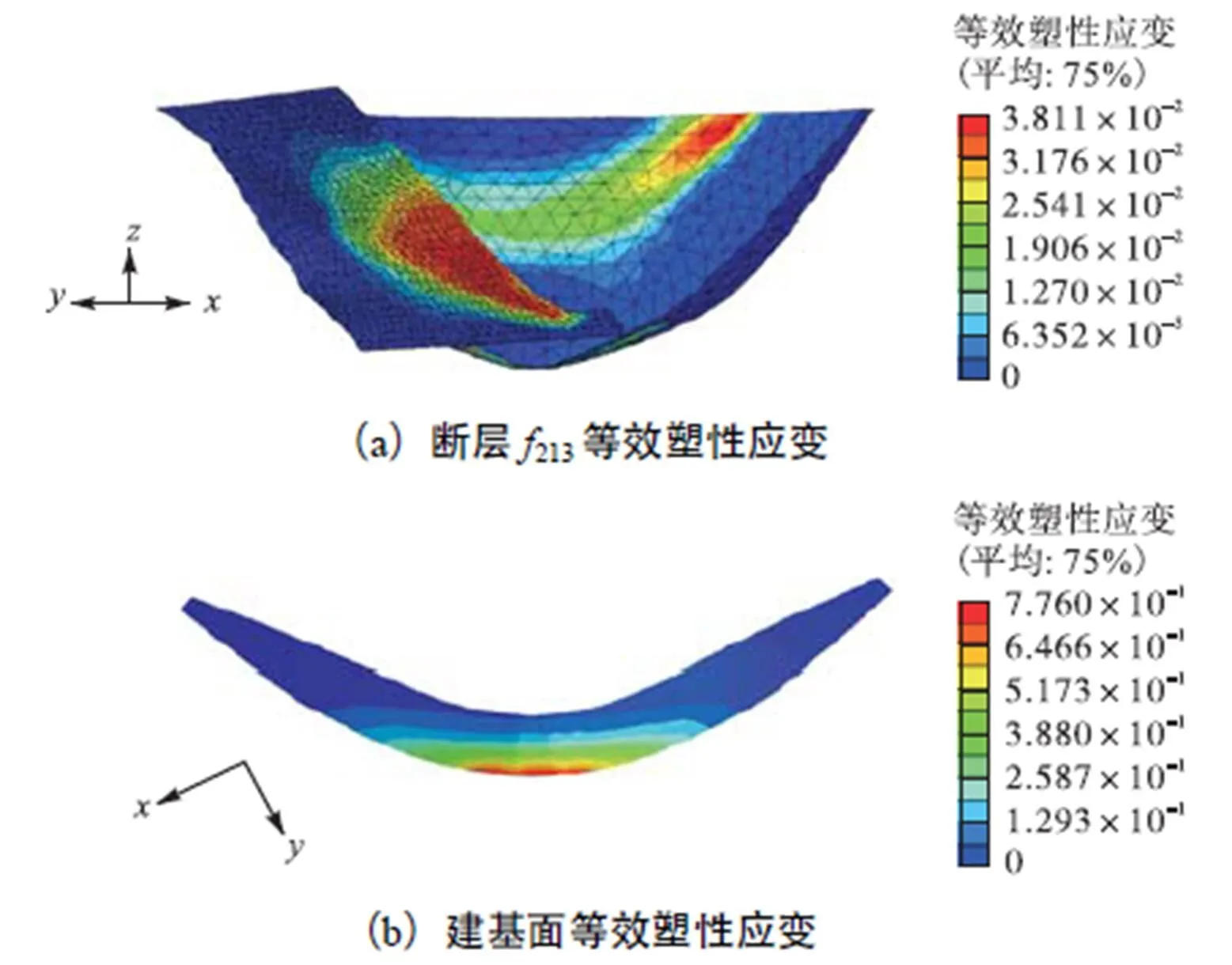
图5 抗滑稳定分析等效塑性应变(超载法)

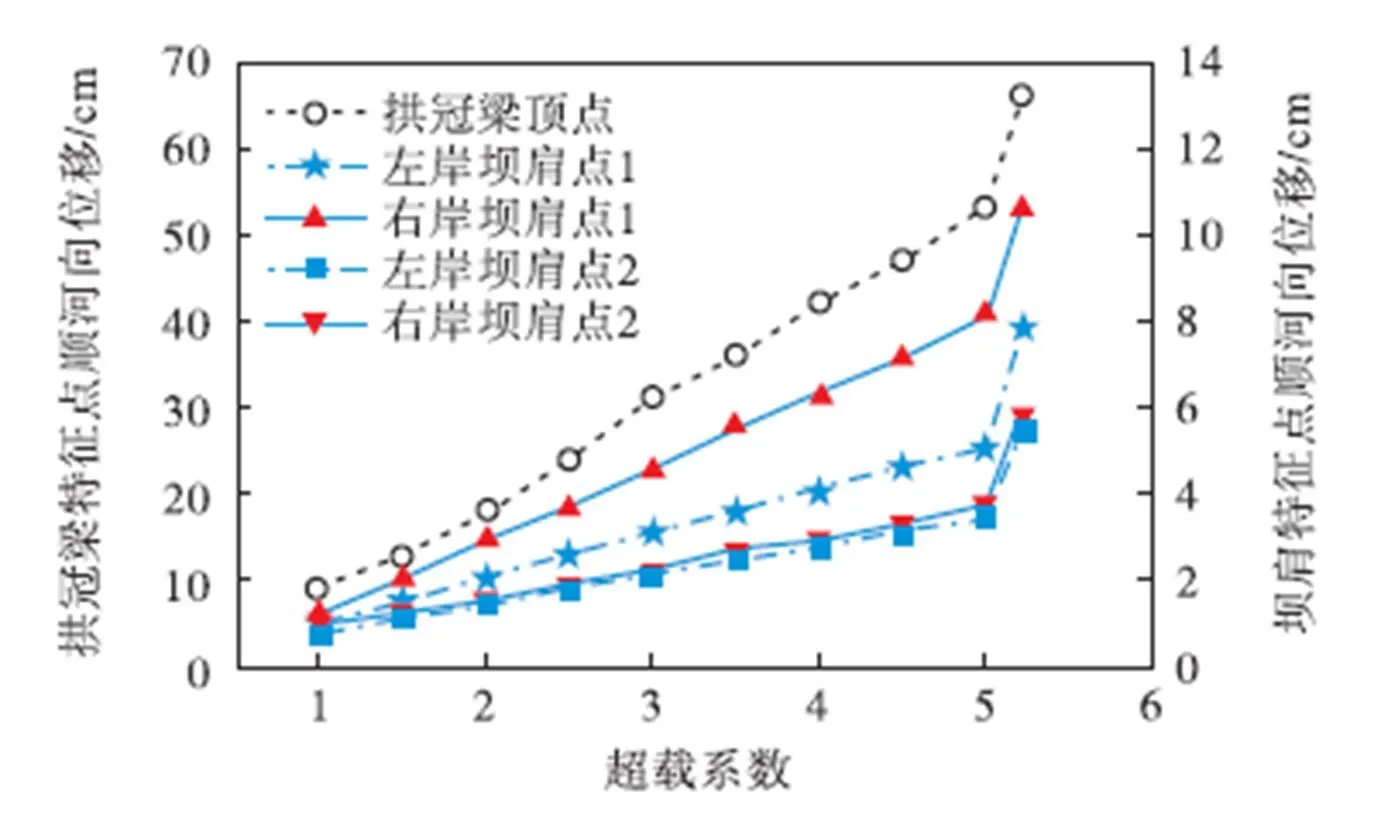
图6 特征点位移随超载系数变化曲线

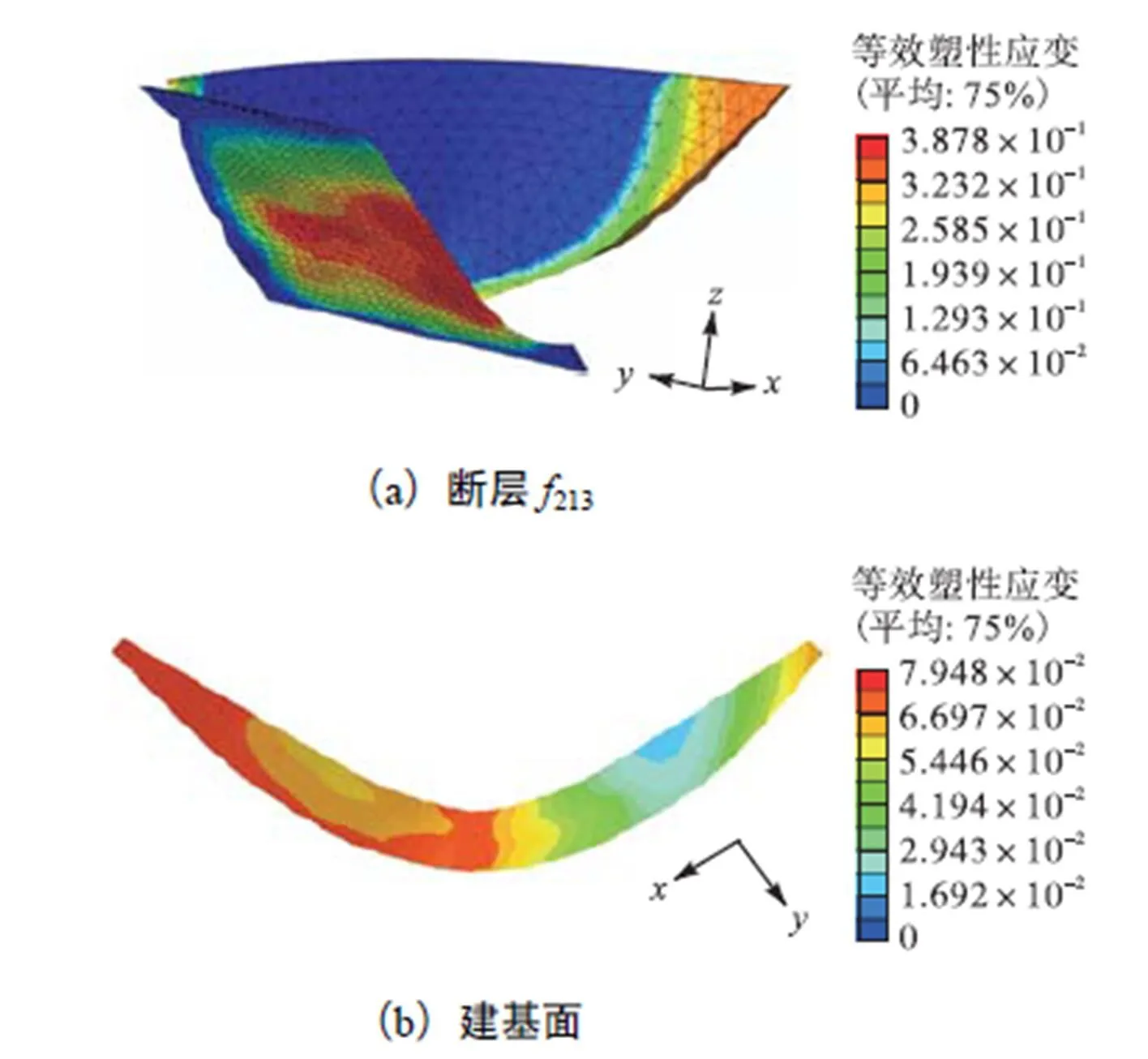
图7 抗滑稳定分析等效塑性应变(强度折减法)

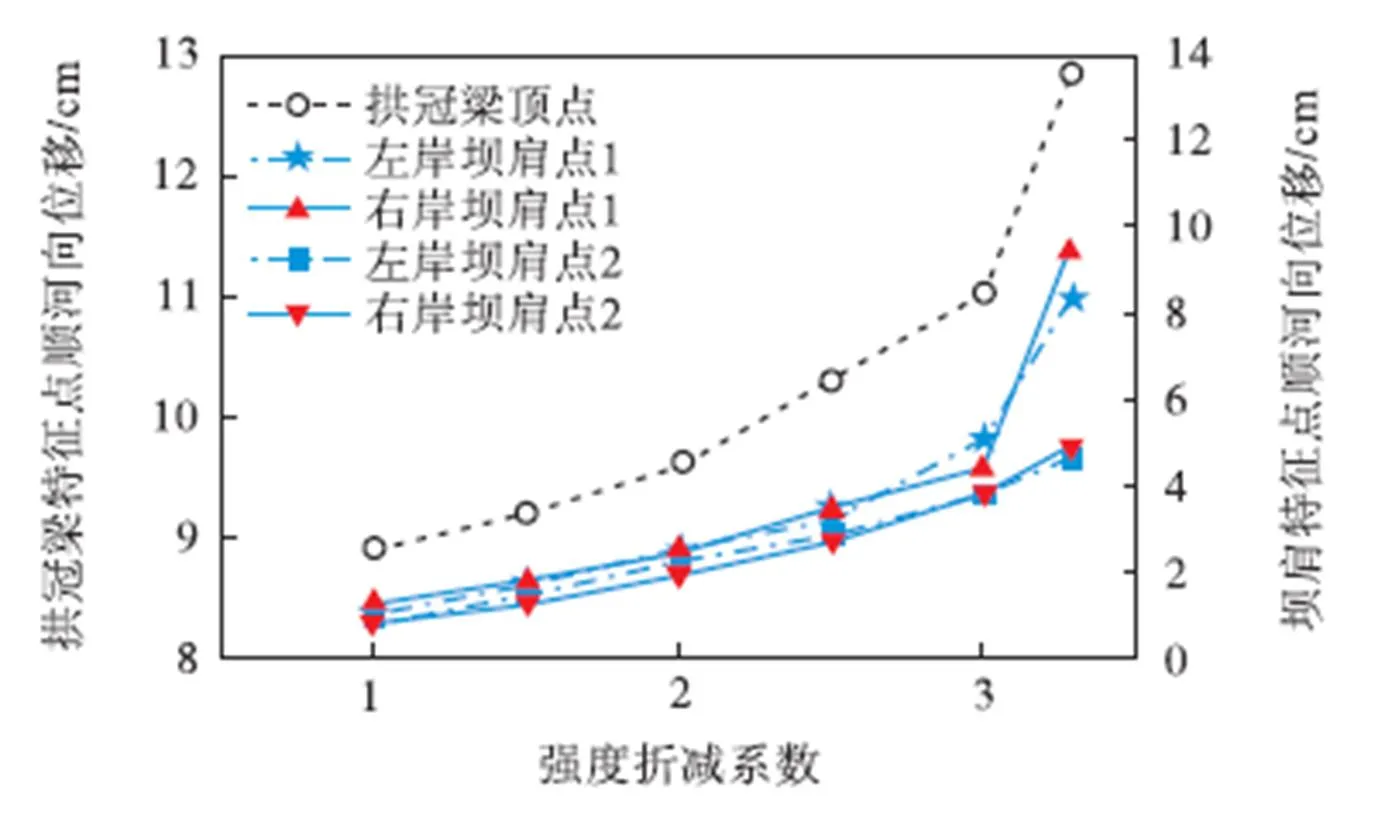
图8 特征点位移随强度折减系数变化曲线

另外，本文对位置参数下考虑流固耦合作用的拱坝结构进行三维抗滑稳定分析，可得到相应的超载与强度折减安全系数如表2所示，同在位置参数下考虑流固耦合作用的拱坝抗滑稳定安全系数有所降低，采用超载法和强度折减法分别降低了6.90%和7.34%．

由表2可知，由于超载法和强度折减法的作用方式的差异，导致计算得到的拱坝破坏方式有所不同，因此得到的相应的拱坝抗滑稳定安全系数也存在一定的差异，在具体应用中应针对具体破坏模式进行深入探究．同时坝基流固耦合作用降低了抗滑稳定安全系数，对拱坝抗滑稳定安全不利，接下来将对其进一步研究．为将位置参数下坝体抗滑稳定安全系数扩展到实际工程中不确定区间参数下坝体抗滑稳定可靠度分析，并探究流固耦合作用对抗滑稳定性可靠度的影响，本文分别采用超载法与强度折减法进行拱坝抗滑稳定可靠度分析．

表2 安全系数计算结果

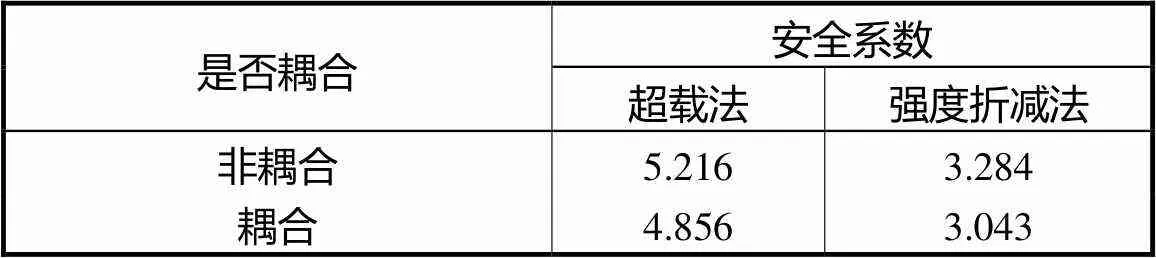
Tab.2 Results of safety factor

3.4.2 流固耦合作用下渗流场分析

分别对非耦合与耦合条件下的拱坝渗流场进行分析，如图9所示．对比图9(a)和图9(b)可以得到，考虑流固耦合作用下拱坝的渗流场与不考虑耦合作用相比整体分别变化不大，且由于帷幕和坝体渗透系数较小，可以看出水位线在此处出现明显地降低．

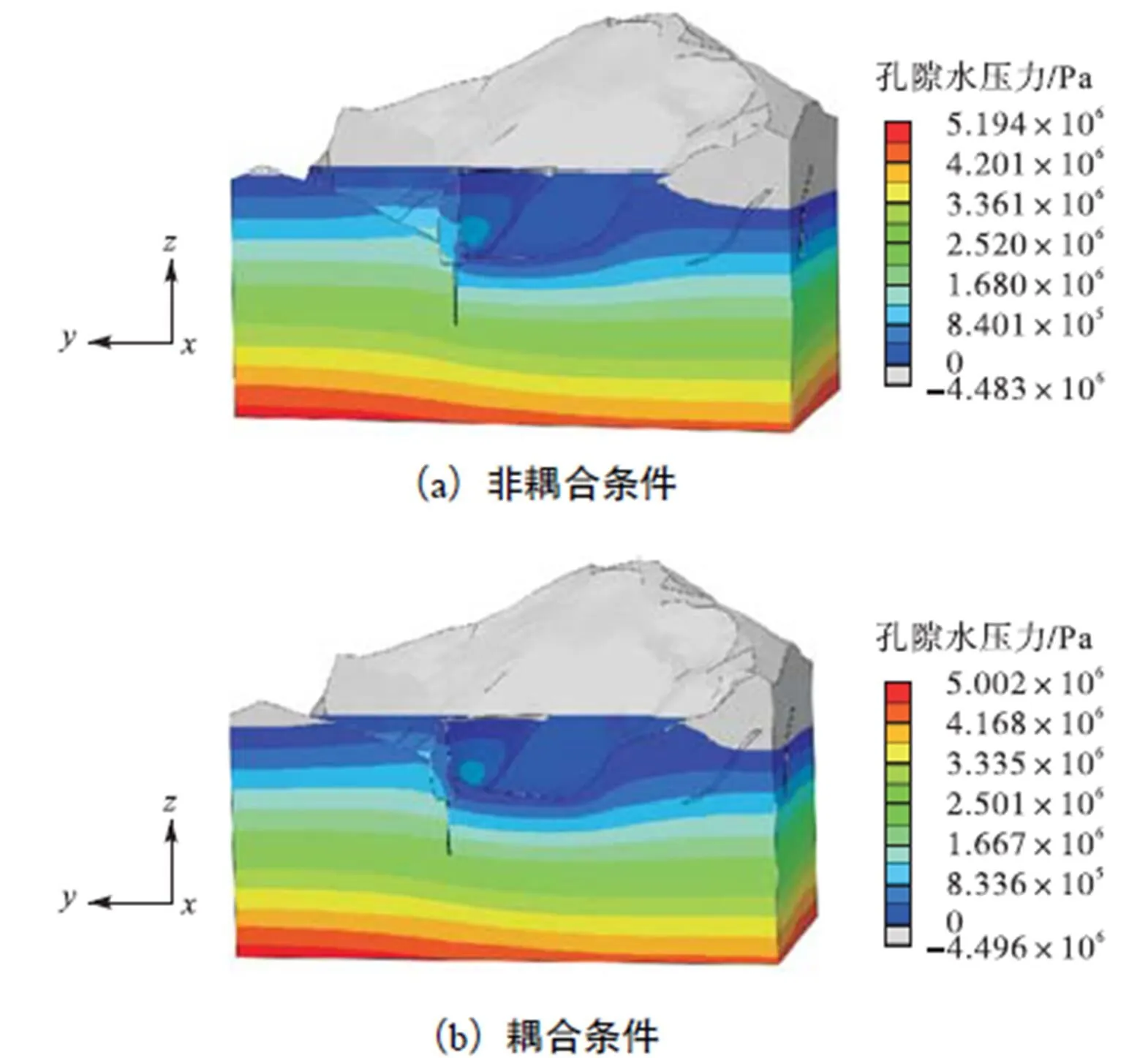
图9 非耦合与耦合条件下孔隙水压力云图

为了更加直观地体现渗流关系，研究提取了等势线云图如图10所示．对比图10(a)和图10(b)可以得到，在考虑流固耦合作用时，从上游至下游，由于水头损失，等势线逐渐降低，同时由于在上游水压力的作用下，坝踵受拉压力导致渗透系数增大，坝趾受压应力导致渗透系数减小，因此在非耦合条件下，靠近坝踵部位等势线较为密集，靠近坝踵部位等势线较为稀疏，而在耦合条件下，靠近坝踵部位等势线相对稀疏，而靠近坝趾部位相对密集．与非耦合情况相比，考虑流固耦合作用能够较为合理地反映渗流场的 变化．

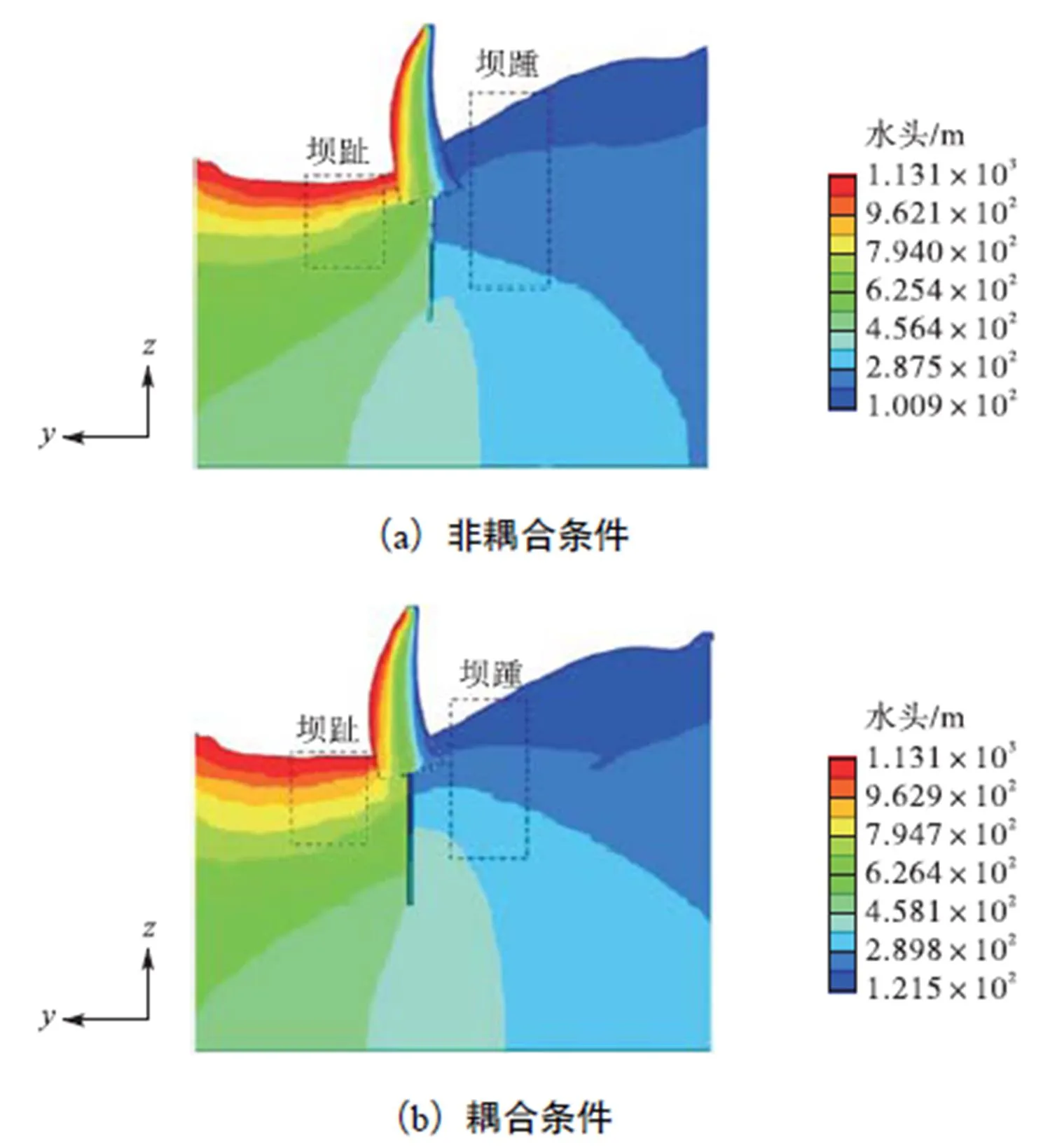
图10 非耦合与耦合条件下等势线云图

3.4.3 流固耦合作用下拱坝抗滑稳定可靠度分析

为对流固耦合作用下的拱坝抗滑稳定可靠度进行合理评价，研究首先根据可靠度与安全系数的关 系[27]，定义极限状态函数为

(13)

考虑到工程中缺乏足够的统计信息情况下结构参数的不确定性，根据表1所列材料性质，采用中心复合法进行抽样，通过2＋1次确定性超载法有限元计算得到一组输入与输出变量，之后根据公式(5)构造响应面函数．图11(a)和图11(b)分别为采用超载法计算时非耦合与耦合情况下非概率可靠度指标的寻优过程，同理可得到采用强度折减法计算时各工况下非概率可靠度，计算结果如表3所示．

对比表2与表3，结合公式(13)，考虑实际工程中参数不确定性后，拱坝抗滑稳定安全系数低于位置参数下安全系统，同时，在采用超载法和强度折减法进行计算时，考虑流固耦合作用下拱坝的抗滑可靠度指标与不考虑流固耦合作用相比分别降低了7.14%和7.87%，说明在流固耦合作用下，渗流场将对拱坝应力场产生影响，拱坝的抗滑可靠度有所降低，而未考虑流固耦合作用下的可靠度评价高估了拱坝的可靠度，这对工程安全不利．因此，在对拱坝进行抗滑可靠度分析时，应充分考虑坝基岩体流固耦合作用的影响．

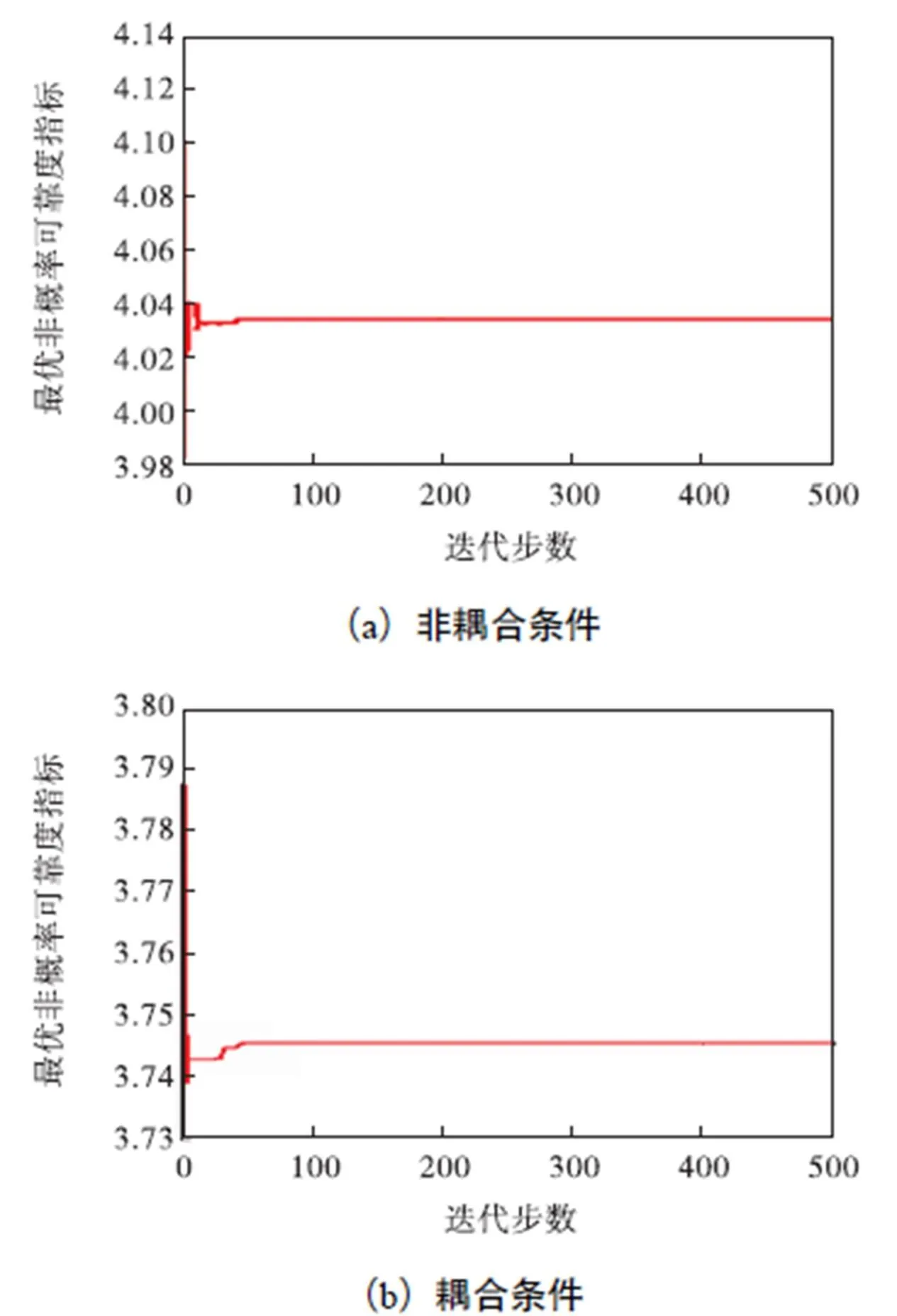
图11 非概率可靠度指标寻优过程(超载法)

表3 非概率可靠度指标计算结果

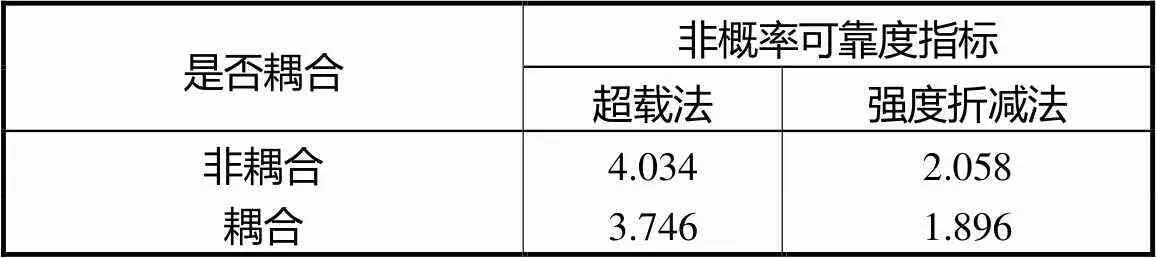
Tab.3 Results of non-probability reliability indexes

4 结 论

本文基于凸模型理论，提出了考虑流固耦合作用下的拱坝三维抗滑稳定非概率可靠度分析方法．结合实际拱坝工程，探究了在考虑岩体参数与荷载不确定性条件下的坝基流固耦合作用对拱坝抗滑稳定可靠度的影响，所得结论如下．

(1) 与非耦合情况相比，考虑了流固耦合作用后，能够较为合理地反映渗流场的变化，同时未考虑流固耦合作用下的可靠度评价高估了拱坝的可靠度，这对工程安全不利，因此进行考虑拱坝坝基岩体流固耦合作用对结构抗滑稳定性影响的研究是十分必 要的．

(2) 研究证明了采用非概率可靠度方法对缺乏足够统计信息情况下的拱坝进行抗滑稳定可靠度分析是可行的．

(3) 采用超载法与强度折减法对拱坝的抗滑安全系数进行计算时，因其作用方式不同导致其破坏模式有所差异，所得超载抗滑安全系数高于强度折减抗滑安全系数．同时两者破坏中右岸坝肩近坝断层213均产生明显塑性破坏，因此建议工程中应对其进行加固处理．

本文研究主要目的为探究坝基渗流场与应力场耦合作用对高拱坝抗滑稳定可靠度的影响，故并未考虑温度场的影响，目前岩土体工程流-固-热耦合已经成为各学者研究的重点，故将在以后的研究中逐步 完善．

［1］ Dhakal S. Implications of transportation policies on energy and environment in Kathmandu Valley, Nepal[J]. Energy Policy，2003，31(14)：1493-1507.

［2］ 任青文. 高拱坝安全性研究现状及存在问题分析[J]. 水利学报，2007，38(9)：1023-1031.

Ren Qingwen. Status quo and problems on safety analysis of high arch dam[J]. Journal of Hydraulic Engineering，2007，38(9)：1023-1031(in Chinese).

［3］ 沈 辉，罗先启，李 野，等. 乌东德拱坝坝肩三维抗滑稳定分析[J]. 岩石力学与工程学报，2012，31(5)：1026-1033.

Shen Hui, Luo Xianqi, Li Ye, et al. Three-dimensional stability analysis of dam abutment of Wudongde arch dam[J]. Chinese Journal of Rock Mechanics and Engineering，2012，31(5)：1026-1033(in Chinese).

［4］ 井向阳，常晓林，周 伟，等. 高拱坝施工期温控防裂时空动态控制措施及工程应用[J]. 天津大学学报：自然科学与工程技术版，2013，46(8)：705-712.

Jing Xiangyang，Chang Xiaolin，Zhou Wei，et al. Spatial-temporal dynamic control framework of temperature control and crack prevention in construction of concrete arch dams and its engineering application[J]. Journal of Tianjin University：Science and Technology，2013，46(8)：705-712(in Chinese).

［5］ Ding Zelin，Wang Qianqian，Wang Jing. Analysis on stability of an Arch Dam with interlayer shear zones[J]. KSCE Journal of Civil Engineering，2016，20(6)：2262-2269.

［6］ Su Huanzhi，Li Jinyou，Wen Zhiping，et al. Dynamic non-probabilistic reliability evaluation and service life prediction for arch dams considering time-varying effects[J]. Applied Mathematical Modelling，2016，40(15/16)：6908-6923.

［7］ 陈在铁, 任青文. 高拱坝安全分析中的不确定性因素研究[J]. 南京理工大学学报，2006，30(6)：718-722.

Chen Zaitie, Ren Qingwen. Uncertainty factors in high arch dam safety analysis[J]. Journal of Nanjing University of Science and Technology，2006，30(6)：718-722(in Chinese).

［8］ Ben-Haim Y. Convex models of uncertainty in radial pulse buckling of shells[J]. Journal of Applied Mechanics，1993，60(3)：683-688.

［9］ Elishakoff I, Elisseeff P, Glegg S A L. Non-probabilistic, convex-theoretic modeling of scatter in material properties[J]. AIAA Journal，2012，32(4)：843-849.

［10］ 邱志平. 非概率集合理论凸方法及其应用[M]. 北京：国防工业出版社，2005.

Qiu Zhiping. Convex Method based on Non-Probabilistic Set-Theory and Its Application[M]. Beijing: National Defense Industry Press，2005(in Chinese).

［11］ 曹文贵，翟友成，王江营，等. 区间非概率可靠性方法在岩溶区稳定性分析中的适用性研究[J]. 岩土力学，2015，36(10)：2955-2962.

Cao Wengui，Zhai Youcheng，Wang Jiangying，et al. Applicability of interval non-probabilistic reliability method in analyzing the stability of karst area[J]. Rock and Soil Mechanics，2015，36(10)：2955-2962(in Chinese).

［12］ Zhu Xiaobin, Wang Xiaoling, Liu Minghui, et al. Channel stability analysis by one-way fluid structure interaction：A case study in China[J]. Transactions of Tianjin University，2017，23(5)：451-460.

［13］ 秦红军，陈 松. 软黏土地基流固耦合非线性力学行为的有限元数值分析[J]. 岩土工程学报，2017，39(增1)：256-260.

Qin Hongjun，Chen Song. FEM analysis of nonlinear mechanical behavior of fluid-solid coupling for soft clay foundation[J]. Chinese Journal of Geotechnical Engineering，2017，39(Suppl1)：256-260(in Chinese).

［14］ Zhu Xiaobin，Wang Xiaoling，Li Xiao，et al. A new dam reliability analysis considering fluid structure interaction[J]. Rock Mechanics and Rock Engineering，2017(2)：1-12.

［15］ 王晓玲，刘长欣，李瑞金，等. 大坝基岩单裂隙灌浆流固耦合模拟研究[J]. 天津大学学报：自然科学与工程技术版，2017，50(10)：1037-1046.

Wang Xiaoling，Liu Changxin，Li Ruijin，et al. Fluid-solid coupling simulation of single fracture grouting in dam bedrock[J]. Journal of Tianjin University：Science and Technology，2017，50(10)：1037-1046(in Chinese).

［16］ 吴永康，王翔南，董威信，等. 考虑流固耦合作用的高土石坝动力分析[J]. 岩土工程学报，2015，37(11)：2007-2013.

Wu Yongkang，Wang Xiangnan，Dong Weixin，et al. Dynamic analysis of a high earth-rockfill dam considering effects of solid-fluid coupling[J]. Chinese Journal of Geotechnical Engineering，2015，37(11)：2007-2013(in Chinese).

［17］ 林 鹏，刘晓丽，胡 昱，等. 应力与渗流耦合作用下溪洛渡拱坝变形稳定分析[J]. 岩石力学与工程学报，2013，32(6)：1145-1156.

Lin Peng，Liu Xiaoli，Hu Yu，et al. Deformation stability analysis of Xiluodu arch dam under stress-seepage coupling condition[J]. Chinese Journal of Rock Mechanics and Engineering，2013，32(6)：1145-1156(in Chinese).

［18］ 王 瑞，沈振中，陈孝冰. 基于COMSOL Multiphysics的高拱坝渗流-应力全耦合分析[J]. 岩石力学与工程学报，2013，32(增2)：3197-3204.

Wang Rui，Shen Zhenzhong，Chen Xiaobing. Full coupled analysis of seepage-stress fields for high arch dam based on COMSOL Multiphysics[J]. Chinese Journal of Rock Mechanics and Engineering，2013，32(Suppl 2)：3197-3204(in Chinese).

［19］ 薛娈鸾. 小湾拱坝坝基含排水孔岩体渗流与应力耦合分析[J]. 武汉大学学报：工学版，2013，46(3)：290-294.

Xue Luanluan. Analysis of coupled seepage and stress in Xiaowan arch dam foundation with drainage holes[J]. Engineering Journal of Wuhan University，2013，46(3)：290-294(in Chinese).

［20］ 苏国韶，郝俊猛. 复杂工程结构非概率可靠度分析的高斯过程动态响应面法[J]. 应用基础与工程科学学报，2015，23(4)：750-762.

Su Guoshao，Hao Junmeng. Gaussian process based dynamic response surface method of non-probabilistic reliability analysis for complicated engineering structure[J]. Journal of Basic Science and Engineering，2015，23(4)：750-762(in Chinese).

［21］ 郭书祥，吕震宙，冯元生. 基于区间分析的结构非概率可靠性模型[J]. 计算力学学报，2001，18(1)：56-60.

Guo Shuxiang，Lü Zhenzhou，Feng Yuansheng. A non-probabilistic model of structural reliability based on interval analysis[J]. Chinese Journal of Computational Mechanics，2001，18(1)：56-60(in Chinese).

［22］ 马 超，吕震宙. 隐式极限状态方程的非概率可靠性分析[J]. 机械强度，2009，31(1)：45-50.

Ma Chao，Lü Zhenzhou. Research on non-probabilistic reliability analysis method for implicit limit state function[J]. Journal of Mechanical Strength，2009，31(1)：45-50(in Chinese).

［23］ Zhong Denghua，Li Mingchao，Liu Jie. 3D integrated modeling approach to geo-engineering objects of hydraulic and hydroelectric projects[J]. Science in China Series E：Technological Science，2007，50(3)：329-342.

［24］ 钟登华，鲁文妍，刘 杰，等. 复杂地质条件下地下洞室曲面块体地震响应分析[J]. 天津大学学报：自然科学与工程技术版，2014，47(6)：471-478.

Zhong Denghua, Lu Wenyan, Liu Jie, et al. Surface-block identification and seismic response analysis of underground structures under complicated geological conditions[J]. Journal of Tianjin University：Science and Technology，2014，47(6)：471-478(in Chinese).

［25］ 夏 雨，张仲卿，赵小莲，等. 基于非概率可靠度理论的拱坝安全度评价[J]. 水利水运工程学报，2010(3)：79-83.

Xia Yu，Zhang Zhongqing，Zhao Xiaolian，et al. Safety analysis of arch dam based on non-probability theory[J]. Hydro-Science and Engineering，2010(3)：79-83(in Chinese).

［26］ 裴利剑，屈本宁，钱闪光. 有限元强度折减法边坡失稳判据的统一性[J]. 岩土力学，2010，31(10)：3337-3341.

Pei Lijian，Qu Benning，Qian Shanguang. Uniformity of slope instability criteria of strength reduction with FEM[J]. Rock and Soil Mechanics，2010，31(10)：3337-3341(in Chinese).

［27］ 蒋水华，李典庆，黎学优，等. 锦屏一级水电站左岸坝肩边坡施工期高效三维可靠度分析[J]. 岩石力学与工程学报，2015，34(2)：349-361.

Jiang Shuihua，Li Dianqing，Li Xueyou，et al. Efficient three-dimensional reliability analysis of an abutment slope at the left bank of Jinping Ⅰhydropower station during construction[J]. Chinese Journal of Rock Mechanics and Engineering，2015，34(2)：349-361 (in Chinese).

Anti-Sliding Stability Non-Probabilistic Reliability Analysis for Arch Dam Considering Fluid-Solid Coupling Effect

Wang Xiaoling，Liu Minghui，Shi Zuzhi，Zhu Xiaobin，Wang Zhen，Lü Mingming

(State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300350，China)

The anti-sliding stability reliability analysis of arch dam is a crucial part of dam safety evaluation，the results of which are related to the dam operation and safety，hence it has important research significance．The existing study mostly adopted probabilistic reliability method．However，due to insufficient statistical information in practical engineering，it is difficult to obtain the exact probability distributions of parameter variables．Besides，there is short of research on anti-sliding stability reliability considering fluid-solid coupling of dam foundation．To address these limitations，based on convex set theory，a non-probabilistic reliability analysis of three dimensional anti-sliding stability for arch dam considering fluid-solid coupling effect was proposed．First，the three dimensional unified model of engineering geology was established．Next，considering the fluid-solid coupling in dam foundation，the anti-sliding stability non-probabilistic reliability was conducted by using overload and strength reduction methods．The results show that it is feasible to analyze the anti-sliding stability reliability of arch dam with meager statistical information by the proposed approach，and the safety assessment of arch dam is overestimated when the fluid-solid coupling effect is neglected，which is unfavorable to engineering safety．

arch dam；anti-sliding stability；fluid-solid coupling；non-probabilistic reliability；finite element method

10.11784/tdxbz201805057

TV37；TV61

A

0493-2137(2019)05-0483-09

2018-05-25；

2018-07-04.

王晓玲（1968— ），女，博士，教授.

王晓玲，wangxl@tju.edu.cn.

国家自然科学基金资助项目(51439005，51339003)；国家自然科学基金雅砻江联合基金资助项目(U1765205).

the National Natural Science Foundation of China(No. 51439005，No. 51339003)，the Joint Funds of the National Natural Science Foundation of China(No. U1765205).

(责任编辑：王晓燕)