基于改进型变步长扰动观察法的最大功率点跟踪策略

宁 佩，周惠媛，胡嘉昕，王波波

（广东工业大学 信息工程学院，广东 广州 510006）

0 引 言

太阳能直接辐射到地球的能量丰富、分布广泛，对环境无污染，是国际社会公认的理想新能源。光伏发电是太阳能的重要利用形式之一。由硅半导体构成的光伏电池能够把光能转化为电能，而光伏电池的输出电压和输出电流容易受到光照强度、温度等外界环境的影响，呈现复杂的非线性输出特性。当光照强度、温度变化时，存在的唯一最大功率点（Maximum Power Point，MPP）随之变化。为了使当前工作点始终工作在最大功率点处，最大功率点跟踪技术（Maximum Power Point Tracking，MPPT）成为光伏发电系统的一个重要环节[1]。目前，常用的最大功率跟踪方法有电导增量法、扰动观察法和模糊控制等。其中，扰动观察法因效率高、实现简单得到了广泛应用。定步长扰动观察法在选取步长时无法兼顾光伏发电系统的动态响应速度和稳态响应精度[2]；而变步长扰动观察法在光照剧烈变化时会发生误判并产生剧烈的震荡。针对上述问题，本文提出了一种基于符号变量判断的扰动观察法。该算法在变步长扰动观察法的基础上增加滞环环节，通过双向扰动得出符号变量的值来确定扰动方向，使控制系统的跟踪速度与跟踪精度满足需求，并有效抑制了在环境突变时最大功率点处的误判问题。

1 光伏电池的数学模型及仿真

光伏电池受到光照时，光伏电池的两端产生电势差。根据量子理论、光伏电池的内部结构和输出特性，得到光伏电池的等效电路，如图1所示。

图1 单个光伏电池的模型

光伏电池的输出电压电流表达式为：

式中，I为光伏电池的输出电流；I0为二极管反向饱和电流；Iph为光照激发电流；Rs为光伏电池的等效串联电阻；Rsh为光伏电池的等效并联电阻；k为玻尔兹曼常数；A为PN结的理想因子；q为单位电子电荷量；T为外界环境温度。设光伏电池的开路电压为为Uoc、短路电流为Isc、最大功率点电压为Um、最大功率点电流为Im

[3-4]。一般而言，并联电阻Rsh很大，串联电阻Rs很小，故式（1）可以简化为：

在标准条件下（光照强度Sref=1 000 W/m2、温度Tref=25 ℃），假定光照激发电流Iph=Isc，光伏电池的输出特性可表示为：

根据开路条件和系统位于最大功率点的相关约束，可得：

实际情况和标准条件下，辐射强度差ΔS和环境温度差ΔT分别为：

为明确外界环境对输出特性曲线的影响，在Matlab/Simulink中建立以光照强度和温度为因变量的光伏电池数学模型。系统仿真参数设置如下：Uoc=21.5 V，Isc=0.65 A，Um=18 V，Im=0.56 A。在环境温度为25 ℃、光照强度为1 000 S/m2时，光伏电池输出的最大功率Pm=10.08 W，如图2所示。

由仿真可知，光伏电池的输出特性曲线呈现非线性状态，不管光照强度和温度如何变化，总存在唯一的最大功率点，只有当前工作点工作在最大功率点处，光伏系统输出效率最大，故需要采用最大功率点跟踪技术来控制光伏电池的实时输出最大功率。

2 基于符号变量判断的变步长扰动观察法

2.1 传统扰动观察法的局限性分析

扰动观察法是每隔一段时间增加或减少输出电压并观测输出功率变化方向决定下一步输出电压是增大还是减小。传统的扰动观察法中，步长为固定值，动态响应精度和稳态响应精度无法同时兼顾。步长较大时，系统对外界环境变化的响应速度快，但会导致工作点在最大功率点附近振荡；步长较小时，提高了系统的稳态响应精度，但对外界环境变化的动态响应速度变慢，降低了光伏系统的发电效率[2-7]。因此，为了改善扰动观察法的跟踪效果，要兼顾光伏发电系统动态响应速度和稳态下的控制精度。

图2 光伏电池的输出特性曲线

为解决步长选取引发的光伏系统动态响应速度和稳态响应精度之间的矛盾，可分析光伏电池当前工作电压U和最大功率点MPP电压Umax之间的关系。当U＜Umax时，当前工作点运行在MPP左边，功率对电压导数比的绝对值在接近MPP时逐渐变小；当U＞Umax时，当前工作点运行在MPP右边， 在远离MPP时逐渐变大[2,7]。基于此，步长的更新规则为：

式中，dP为第k次扰动后与第k-1次扰动后的功率差；dU为第k次扰动后与第k-1次扰动后的电压差；m为比例因子，由系统特性决定；f(i)为符号变量，取1和-1。

在光照强度稳定或变化缓慢的情况下，此算法的步长更新规则能够兼顾光伏系统的动态和稳态性能，但在光照强度突变时无法有效稳定在最大功率点处[5-8]。当光照强度突然变化时，dP值突变，使得值突变，从而在最大功率点处出现误判并产生严重的振荡现象，降低了稳态精度。基于此，本文提出了一种新型的扰动观察法。该方法是在变步长扰动观察法的基础上增加滞环环节，在滞环宽度内双向扰动，得出两次符号变量的值确定下一步的扰动方向，不仅避免了光照强度突变时出现的误判现象，而且满足了动态响应速度和稳态响应精度的要求。

2.2 扰动观察法方向的判断

扰动方向的判断如图3所示。利用当前时刻与前一时刻的电流差值dI和电压差值dV，可计算得dP，即可得dP×dV。通过判断dP×dV的正负，可确定当前工作点的位置，即通过符号变量f(i)的值确定下一步扰动方向，从而向最大功率点逼近；若dP×dV=0，则表明在最大功率点处；若dP×dV＞0，则表明最大功率点在当前工作点右侧；若dP×dV＜0，则表明最大功率点在当前工作点左侧[9]。

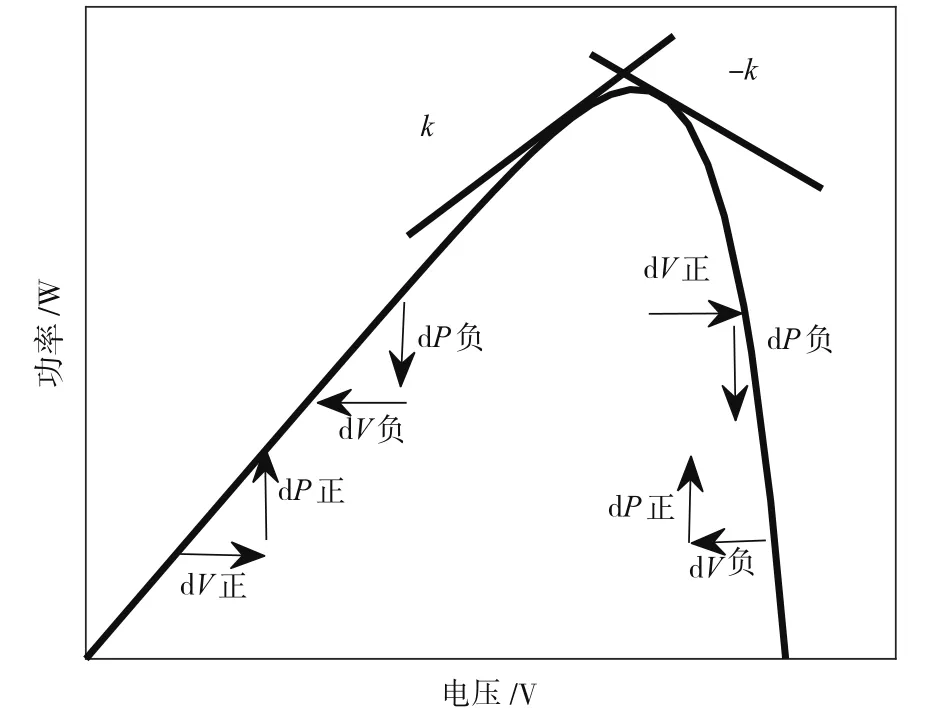
图3 扰动观察法的方向判断

2.3 基于符号变量值的扰动观察法方向判断

为有效降低在外部环境突变时在最大功率点附近出现误判的情况，在变步长扰动观察法方向判断的基础上增加滞环环节。滞环环节选取的方法如下：设光伏系统的当前工作点为点A，根据系统特性设置合适的滞环宽度，由点A向两侧扰动相等步长到达点B、点C，既可形成滞环环节[6]。通过A和B、B和C之间的符号变量值，判断当前工作点位置并确认扰动情况。设光伏系统的当前时刻工作点为A，依据判定的扰动方向扰动一小段步长M至C点，之后反向扰动两个步长至B点，如图4所示。

图4 双向扰动的符号变量值

确定三种扰动方向的判定情况。

规则1：如图4 a所示，A向B扰动，若A、B在最大功率点的左边，此时dP×dV＞0，令符号变量f1=1；A向C扰动，若A、C在最大功率点的左边，此时dP×dV＞0，令符号变量f2=1；此时f=f1+f2=2，应增大电压值。

规则2：如图4 b所示，A向B扰动，若A点功率大于B点功率，可认为A、B在最大功率点的右边，此时dP×dV＜0，令符号变量f1=-1；A向C扰动，若A点功率大于C点功率，可认为A、B在最大功率点的左边，此时dP×dV＞0，令符号变量f2=1；此时f=f1+f2=0，表示当前工作点在最大功率点处或者离最大功率点很近且满足精度要求，或者表示外部光照强度变化很快，电压值不变。如图4 d和图4 e所示，表示当前工作点离最大功率点很近并满足精度要求，保持当前电压值不变。

规则3：如图4 c所示，A向B扰动，若A、B在最大功率点的右边，此时dP×dV＜0，令符号变量f1=-1；A向C扰动，若A、C在最大功率点的右边，此时dP×dV＜0，令符号变量f2=-1；此时f=f1+f2=-2，应减小电压值。

初始时，设i为光伏系统的当前工作点，采样当前点的电压U(i)、电流I(i)，并计算其输出功率P(i)，同时令符号变量f=0。根据系统特性设定滞环宽度并令步长为M，由点i向左扰动一个步长M，记为i-1，再从i-1向右扰动两个步长，记为i+1。采样i-1、i+1两点处的电压U(i-1)、U(i+1)，电流I(i-1)、I(i+1)，并计算i-1处的输出功率P(i-1)，i+1处的输出功率P(i+1)。然后，分别求出 dP1、dP2、dU1、dU2，通过 dP1×dU1和dP2×dU2的取值情况决定符号变量的值来判断扰动方向。根据系统特性设定的跟踪精度要求，若当前的工作点满足精度条件dP1＜e或dP2＜e，可调节开关管占空比输出当前工作点功率，然后返回开始处准备判断下一个工作点；若当前工作点不满足精度要求，则调节开关管占空比继续向最大功率点方向扰动。改进算法的流程，如图5所示。

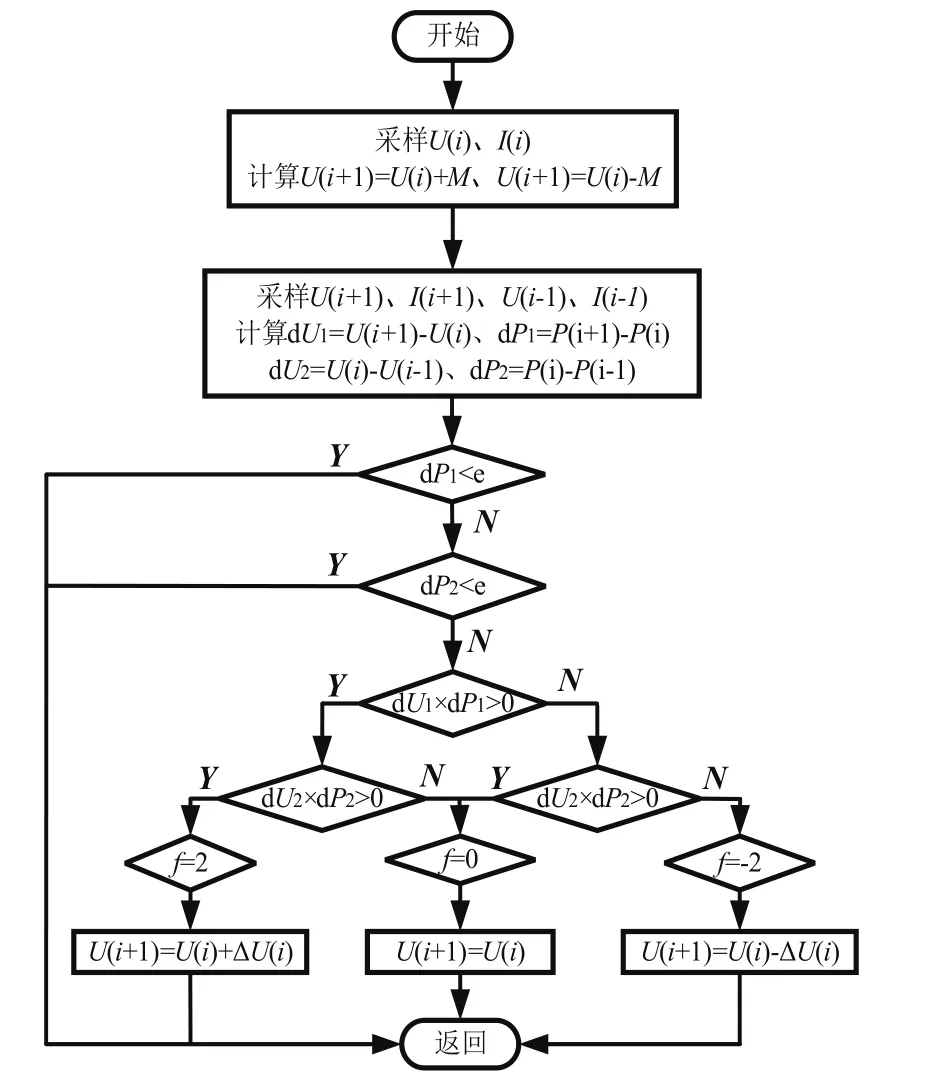
图5 改进算法流程图

3 仿真结果分析

在Matlab/Simulink仿真环境下，基于buck电路建立MPPT算法的仿真模型，系统的整体仿真模型如图6所示。本文利用该仿真模型，分别对变步长扰动观察法和基于符号变量判断的变步长扰动观察法进行仿真。

设温度为定值25 ℃，当t=0.35 s时，光照强度从1 000 S/m2突变到800 S/m2，变步长扰动观察法的仿真波形如图7所示。放大t=0.35 s处的波形，如图8所示。光伏电池的输出功率在光照突变时出现了误判和较大的震荡现象，稳态输出功率为7.79 W，由误判造成功率损耗约为0.075 W，占输出功率的0.96%。

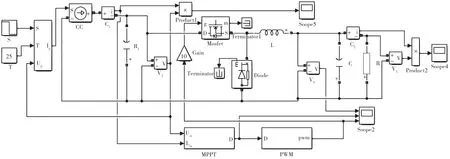
图6 光伏系统仿真模型图

图7 变步长扰动观察法

图8 变步长扰动观察法局部放大图

改进算法的仿真波形如图9所示。放大t=0.35 s处的波形，如图10所示。光照强度突变时，输出功率的误判和震荡得到有效抑制，提高了扰动方向的可靠性，几乎没有损耗产生，提高了光伏系统发电效率。

图9 基于符号变量判断的变步长扰动观察法

图10 基于符号变量判断的变步长扰动观察局部放大图

4 结 论

本文对传统的光伏MPPT算法进行改进，提出了一种增加滞环环节、基于双向符号变量判断的变步长扰动观察法。在光照强度突变时，它与传统的变步长扰动观察法进行了仿真对比。仿真结果显示，该算法具有良好的动态响应速度和稳态跟踪精度，在光照强度突变时能够有效抑制最大功率点处的震荡现象，并避免系统误判的发生，提高了光伏系统的发电效率，具有较高的实用价值。