四轮独立驱动电动汽车行驶状态级联估计

陈特，陈龙,，蔡英凤,，徐兴,，江浩斌,

(1.江苏大学 汽车与交通工程学院，江苏 镇江，212013；2.江苏大学 汽车工程研究院，江苏 镇江，212013)

随着能源危机与环境污染问题的日益严重，以电动汽车为主的新能源汽车得到了汽车行业的关注与广泛研究[1-3]。四轮独立驱动电动汽车的4个轮毂电机皆独立可控，这一优点为车辆主动安全控制、操纵稳定性控制以及转矩节能控制提供了更高的操纵自由度，近年来成为汽车行业的研究热点之一[4]。车辆状态的准确估计是电动汽车精确运动控制不可或缺的一环，基于模型的车辆状态观测器设计可利用低成本传感器实现对重要车辆状态的实时估计，从而替代价格昂贵的传感器，更适于实车应用。因此，很有必要进行四轮独立驱动电动汽车行驶状态估计的研究。目前已有许多车辆行驶状态估计的研究，常见估计方法包括卡尔曼滤波法[5-6]、优化估计法[7]及非线性观测器[8-10]和滑模观测器[11]等。例如LI等[5]提出了一种基于模型自适应粒子滤波结合小波变换的方法，实现了整车行驶状态的自适应估计。但现有车辆状态估计方面的研究大多是针对传统内燃机汽车[4-10]，针对四轮独立驱动电动汽车的状态估计还较少。例如杨斯琦等[8]提出了一种轮胎力级联估计方法，但设计的观测器需要包括发动机扭矩、转速和轮缸压力等测量输入，对观测器要求较高。HORI等[10]根据车轮旋转动力学方程对车轮转速进行积分来估计轮胎纵向力，但该方法同时对噪声也进行了积分导致估计精度不足。四轮独立驱动电动汽车中，由轮毂电机和轮胎组成的电驱动轮不仅是一个整车控制策略的执行机构，也是一个相对独立的控制单元与信息单元。若能利用电驱动轮的驱动特性，将轮毂电机的电流、转速及母线电压这些易得的低成本传感器信息应用到状态估计中，将能充分利用四轮独立驱动电动汽车的优点，减少估计成本。但目前针对四轮独立驱动电动汽车状态估计的研究并未考虑到这一优势，没有将轮毂电机模型考虑进去[12-13]。徐兴等[14-15]基于电驱动轮模型及其驱动特性实现了轮胎纵向力的估计，但未能将其应用到整车状态估计中。为充分利用四轮独立驱动电动汽车自身优势，本文作者将电驱动轮模型应用到车辆状态估计中，采用自适应高阶滑模观测器对轮胎纵向力进行估计，并基于信息融合滤波算法提出了一种车辆状态级联估计方法。利用仿真和实验验证了所提出估计方法的车辆状态估计效果，为四轮独立驱动电动汽车主动安全控制与转矩优化分配研究提供基础。

1 车辆动力学模型

1.1 三自由度车辆模型

如图1所示，建立具有纵向、侧向以及横摆运动的三自由度车辆动力学模型。图1中，固定在汽车上的动坐标系xoy原点与汽车质心重合，x轴为汽车纵向对称轴，规定向前为正；y轴通过汽车质心，规定向左为正；所有坐标系平面内的角度和力矩以逆时针方向为正，所有矢量的分量以与坐标轴同向为正。忽略悬架以及汽车垂向运动，忽略汽车绕y轴的俯仰运动和绕x轴的侧倾运动，认为汽车各个轮胎的机械特性相同。图1中，车轮1，2，3和4分别对应左前、右前、左后和右后车轮。三自由度车辆模型的动力学方程为

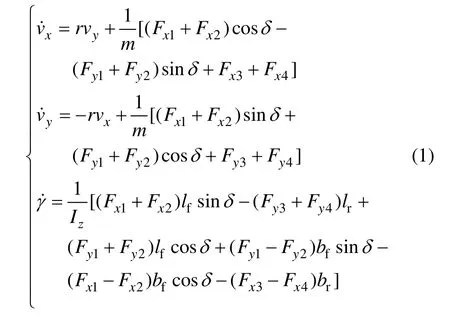
式中：vx为纵向车速；vy为侧向车速；γ为横摆角速度；m为汽车质量；Fxj和Fyj(j=1,2,3,4)分别为轮胎的纵向力和侧向力；δ为前轮转角；Iz为绕z轴的转动惯量；lf为质心距前轴的距离；lr为质心距后轴的距离；bf为前轮距的1/2；br为后轮距的1/2。

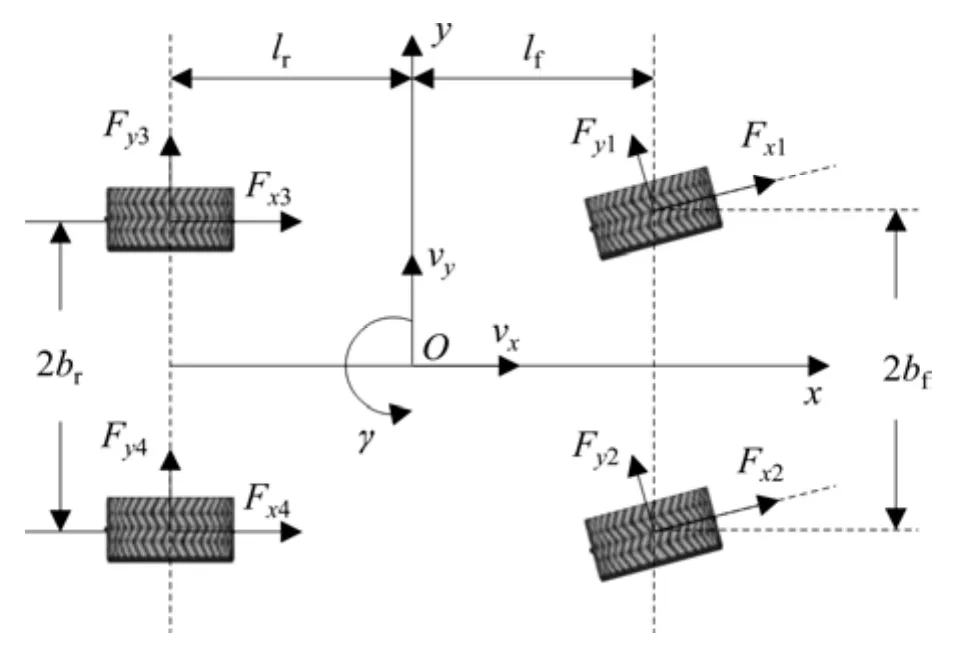
图1 三自由度车辆模型Fig.1 Vehicle model with 3 degree of freedom

1.2 电驱动轮模型

四轮独立驱动电动汽车每个车轮各由一个轮毂电机单独驱动，由轮毂电机和车轮组成的驱动轮是一个独立的驱动单元，驱动轮模型如图2所示。单个车轮的旋转动力学方程为

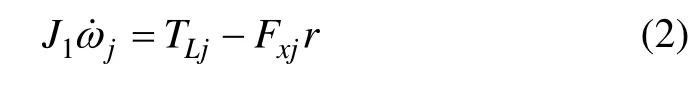
式中：ωj为纵向力Fxj所对应车轮的转速；J1为车轮转动惯量；r为车轮有效半径；TLj为安装于车轮内轮毂电机的负载力矩。

轮毂电机输出轴上的转矩平衡方程为

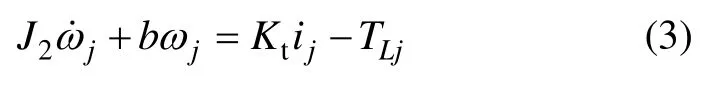
轮毂电机等效电路的动态电压平衡方程为

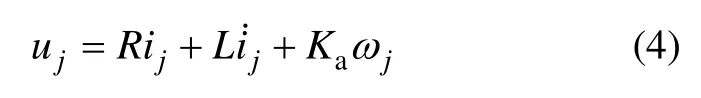
式中：J2为电机转子的转动惯量；b为阻尼系数；Kt为电机转矩常数；ij为线电流；uj为线电压；R为绕组等效线电阻；L为绕组等效电感；Ka为反电动势系数。

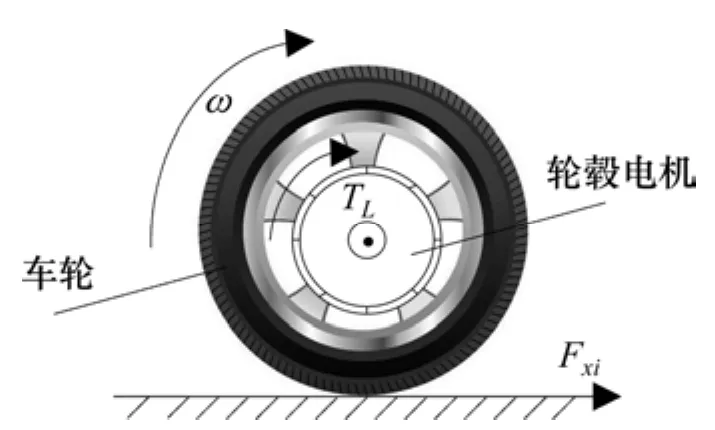
图2 电驱动轮模型Fig.2 Electric driving wheel model

1.3 轮胎模型

采用半经验魔术公式的轮胎模型对轮胎侧向力进行估计，公式为

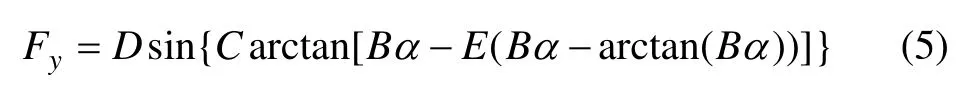
式中：B为刚度因子；C为曲线形状因子；D为峰值因子；E为曲线曲率因子；α为车轮侧偏角。

轮胎模型参数B，C，D和E都与轮胎的垂直载荷相关，各轮胎的垂直载荷为

式中：Fz1，Fz2，Fz3和Fz4为对应轮胎的垂直载荷；h为质心高度；g为重力加速度。

各轮胎侧偏角为

式中：α1，α2，α3和α4为对应轮胎的侧偏角。

2 纵向力观测器设计

2.1 电驱动轮模型精确线性化条件

由式(2)，(3)和(4)联立可得

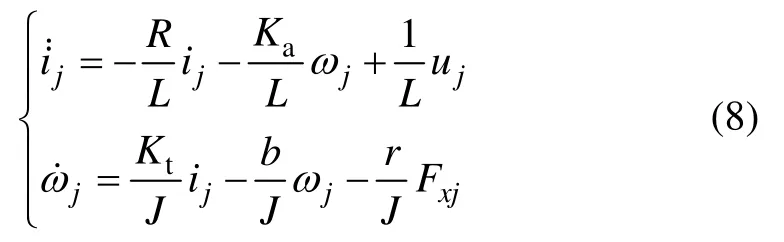
其中：J=J1+J2为电驱动轮转动惯量。设a11=-R/L，a12=-Ka/L，a21=Kt/J，a22=b/J，g1=1/L，g2=-r/J，则电驱动轮模型的系统方程可表示为

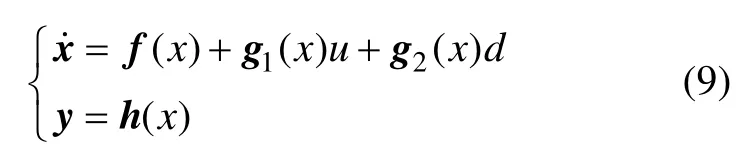
电驱动轮模型(9)为一个2输入2输出的非线性仿射系统，进行李括号运算可得：

因此，矩阵 [g1(x)g2(x)adfg1(x)adfg2(x)]的秩为2，与系统维数相等。经计算可知，向量场D1=[g1]，D2=[g1,g2]，D3=[g1,g2,adfg1]，D4=[g1,g2,adfg1,adfg2]皆为恒向量场，可知D1，D2，D3和D4均是对合的。从而推断电驱动轮模型满足精确线性化条件。

2.2 基于自适应高阶滑模观测器的纵向力估计

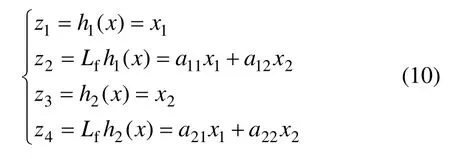
z1和z2与z3和z4都包含状态值电流x1和转速x2的信息，故只取z1和z2来表达坐标变换后的系统。电驱动轮模型转化为

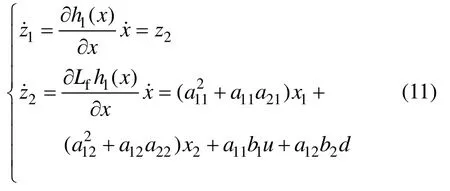
纵向力为模型未知输入量。为了估计纵向力，引入一个新的増广状态量z5。则系统(11)被扩充为

基于超螺旋算法，设计高阶滑模观测器如下

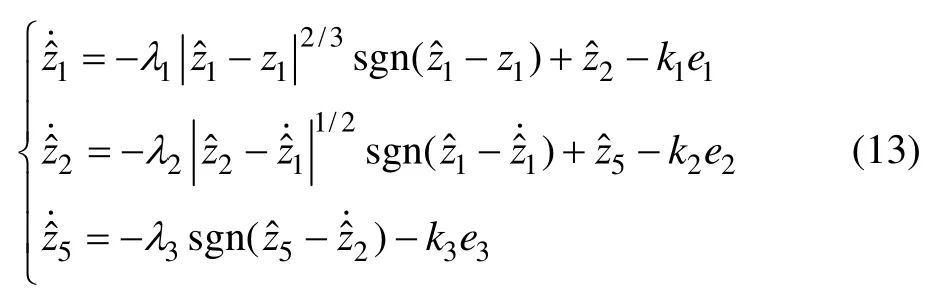
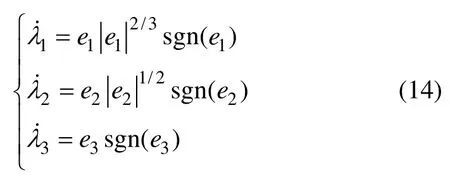
该高阶滑模观测器能同时实现电驱动轮模型坐标变换后的系统状态与系统状态微分的估计，由式(11)和(12)可设计纵向力观测器如下：

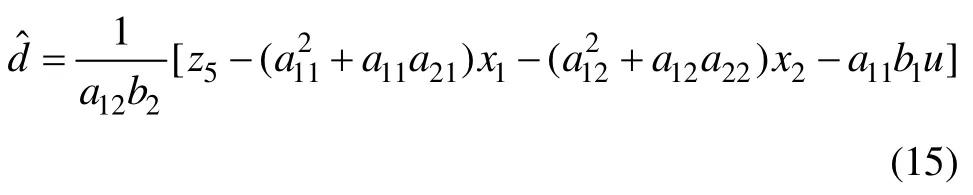
利用该未知输入观测器即可实现纵向力的估计。

3 基于信息融合滤波的车辆状态估计

由三自由度车辆模型，可建立如下离散时间随机动态系统方程：

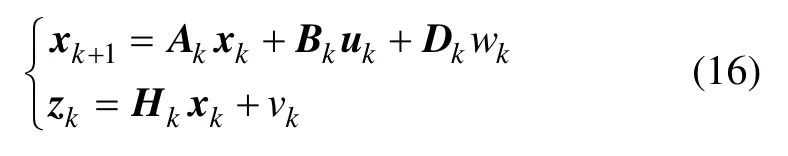
式中：xk为状态向量；zk为量测向量；uk为输入向量；Ak为状态转移矩阵；Bk为输入矩阵；Dk为噪声矩阵；Hk为量测矩阵；wk和vk分别为符合高斯分布的过程噪声和量测噪声。一般的卡尔曼滤波通过对状态协方差矩阵进行分解，来提高实时跟踪能力与数值计算的稳定性。但矩阵分解加大了计算量，估计的实时性受到了一定的限制。

考虑量测信息互不相关，则量测协方差矩阵为对角阵。利用信息融合理论，设

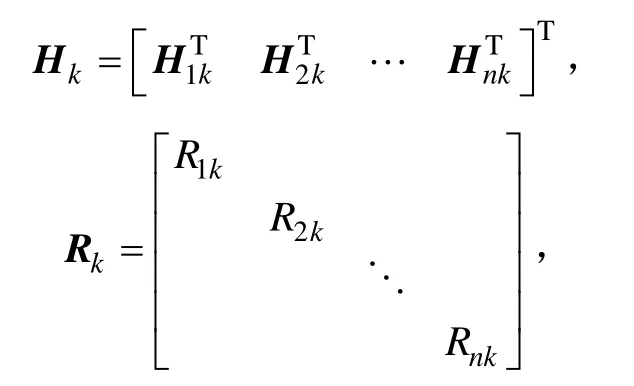
则有

将Rk代入式(17)可得

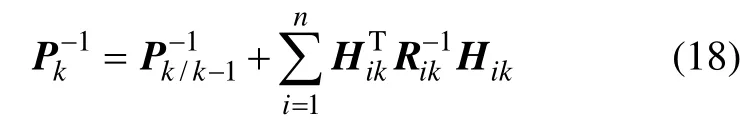
根据矩阵求逆公式，可得

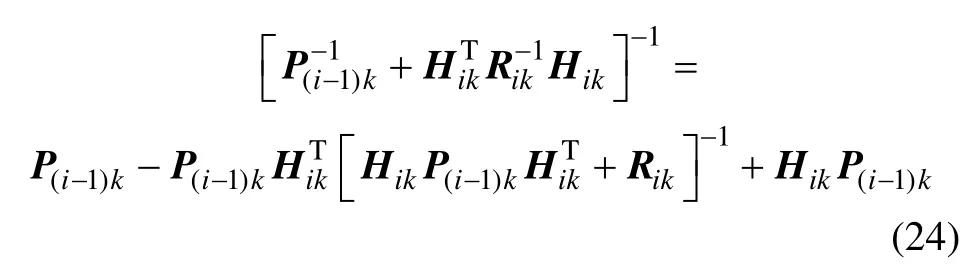
设

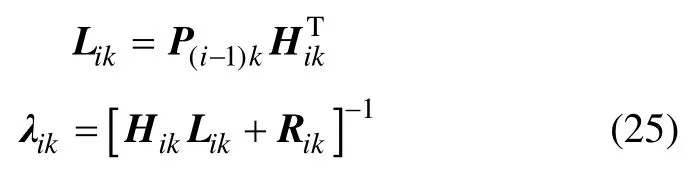
将式(24)和(25)代入式(22)和(23)可得：

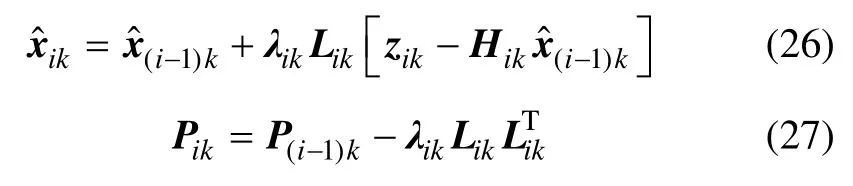
依据式(20)，(21)，(26)和(27)，即可得到系统状态的递推估计值，算法流程图如图3所示。

图3 信息融合滤波流程图Fig.3 Flow chart of information fusion filtering

基于该最优序贯融合滤波算法设计车辆状态联合估计方法，其中状态向量，量测向量，输入向量。ax和ay分别为车辆在大地坐标系上的纵向加速度和侧向加速度，且满足

利用前面所述的纵向力估计方法，针对4个电驱动轮分别设计纵向力观测器，且将所得的纵向力估计值视为虚拟传感器的测量值，从而作为车辆行驶状态级联估计的输入量。根据纵横向车速的滤波估计，可进一步计算出车辆的质心侧偏角为

4 仿真实验

为验证本文提出估计方法的有效性，基于Carsim与Simulink软件搭建了车辆联合仿真平台并进行仿真分析。仿真参数如表1所示。

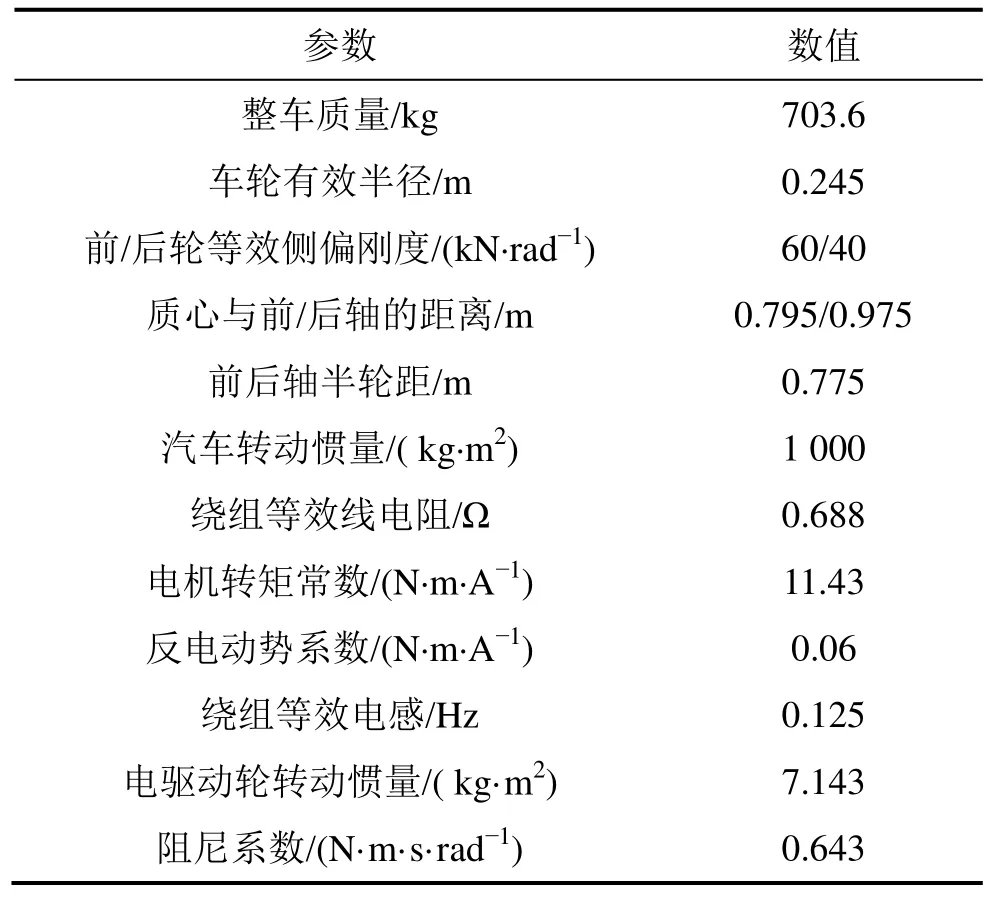
表1 仿真参数Table 1 Simulation parameters

4.1 双移线工况

图4 连续双移线工况Fig.4 Two successive double lane changes (DLC)

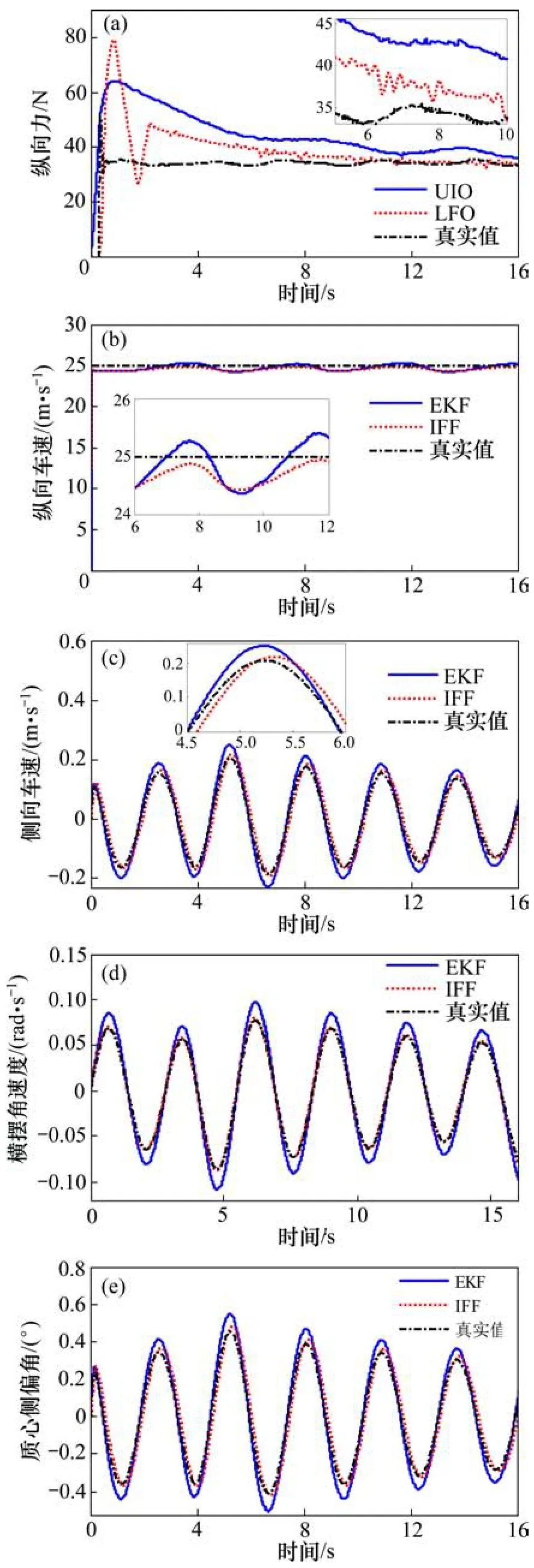
图5 双移线工况仿真结果Fig.5 Simulation results of DLC manoeuvre

为验证所设计的纵向力观测器估计效果，同时考虑到电驱动轮模型含有未知输入的情况，基于电驱动轮模型设计了未知输入观测器(unknown input observer，UIO)[16]与本文设计的纵向力观测器进行对比。首先进行了双移线工况下的道路仿真实验，其中所采用连续双移线工况如图4所示，车速为25 m/s，路面附着系数为0.8。仿真结果如图5所示。由图5(a)可知：本文设计的LFO估计出的纵向力在起步时有一个尖峰，但尖峰顶点相对较小且很快收敛并趋于稳定。车辆起步瞬间，轮毂电机电流瞬间增大，导致纵向力估计在开始阶段波动相对较为剧烈。此外，“抖振”现象是滑模观测器的显著特点，LFO估计的纵向力具有较多的“抖振”，但通过局部放大可以发现振幅相对纵向力的量级来说非常小且逐渐衰弱，证明了LFO设计过程中引入的高阶滑模算法具有较好的动态调节、自适应及抗干扰能力，相比普通的UIO具有更高的估计精度。由于车辆加速瞬间并不是车辆行驶的常态，因此，常态行驶条件下良好的估计性能更加具有工程应用意义，且从整体上来看，LFO的估计效果优于UIO的估计效果。图5(b)～5(e)所示为文中设计的信息融合滤波算法(记为IFF)与扩展卡尔曼滤波算法(记为EKF)的车辆状态估计对比。可以看出两者都能实时跟踪车辆行驶状态，但IFF相比EKF具有更高的估计精度，其估计能力比EKF的优。

4.2 鱼钩工况

为进一步验证提出的估计方法在复杂行驶工况下的估计性能，进行了低附着路面条件下的鱼钩工况仿真验证。仿真时，方向盘转角如图6所示，车速为15 m/s，路面附着系数为0.4，所得仿真结果如图7所示。图7(a)所示为纵向力估计结果对比，与图5(a)相同，此时LFO的实时跟踪能力优于UIO的实时跟踪能力，且收敛更快并趋于稳定。由图7(b)～7(e)可知：当路面附着系数较低，车辆转向变化剧烈且行驶条件较为恶劣时，IFF仍能保持较好的估计效果，从而验证了所提出的估计方法的抗干扰能力与多工况适应能力。

图6 方向盘转角Fig.6 Steering wheel angle

5 实车实验

5.1 底盘测功机台架实验

图7 鱼钩工况仿真结果Fig.7 Simulation results of fishhookmanoeuvre

实验用车为课题组一款改装的四轮独立驱动电动汽车，由于目前该车尚未装备轮胎力传感器，纵向力无法通过传感器实时测得，故在底盘测功机实验台架上进行纵向力估计的实验验证。图8所示为底盘测功机台架实验原理图。基于快速原型实现车辆控制，利用 CAN总线采集到的电流、电压、转速值作为纵向力观测器的输入，并将估计到的纵向力与底盘测功机数据采集系统测得的真实纵向力进行对比验证。本文选取右前电驱动轮的实验数据进行验证，结果如图9所示。从图9可知：在车辆启动时纵向力估计会有一定的偏差但偏差相对较小，当车辆匀速行驶时，纵向力估计趋于稳定且具有较高的估计精度。

图8 底盘测功机台架实验原理图Fig.8 Schematic diagram of bench test on chassis dynamometer

图9 纵向力估计结果Fig.9 Longitudinal force estimation result

5.2 实车道路实验

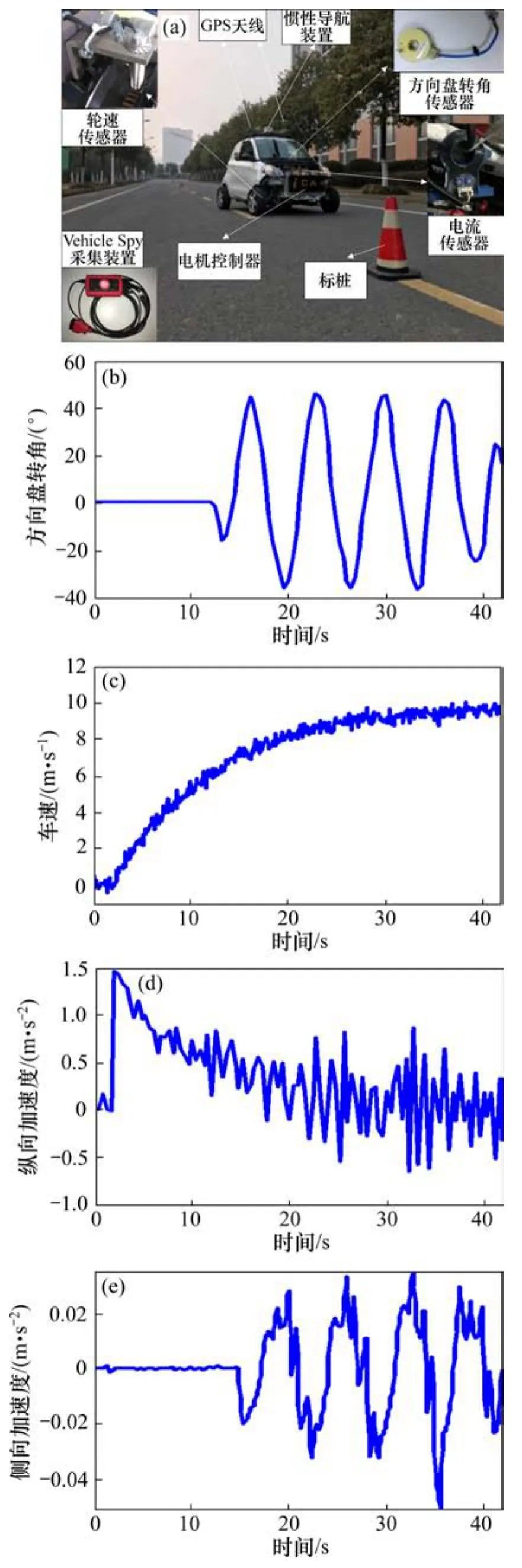
图10 实车道路实验Fig.10 Vehicle road test

实车道路实验场景及实验装置如图10(a)所示，道路上每隔30 m安放标桩，车辆通过换道避障进行蛇形道路实验，利用高精度差分GPS采集纵横向车速及质心侧偏角，惯性装置采集纵横向加速度及横摆角速度，轮速、电流及电压由相应的传感器测得，车辆前轮转角根据方向盘转角换算得到，经由 CAN总线采集传感器信息并通过Vehicle Spy进行传感器数据记录，所得的车辆状态如图10(b)～(e)所示。纵向力观测器已进行了底盘测功机台架实验验证，因此将道路实验所得纵向力估计值作为滤波器的虚拟传感器量测输入，所得车辆状态估计结果如图11所示。从图11可知：2种滤波算法都有较好的估计效果，且IFF相比EKF实时估计能力更好，估计精度更高。

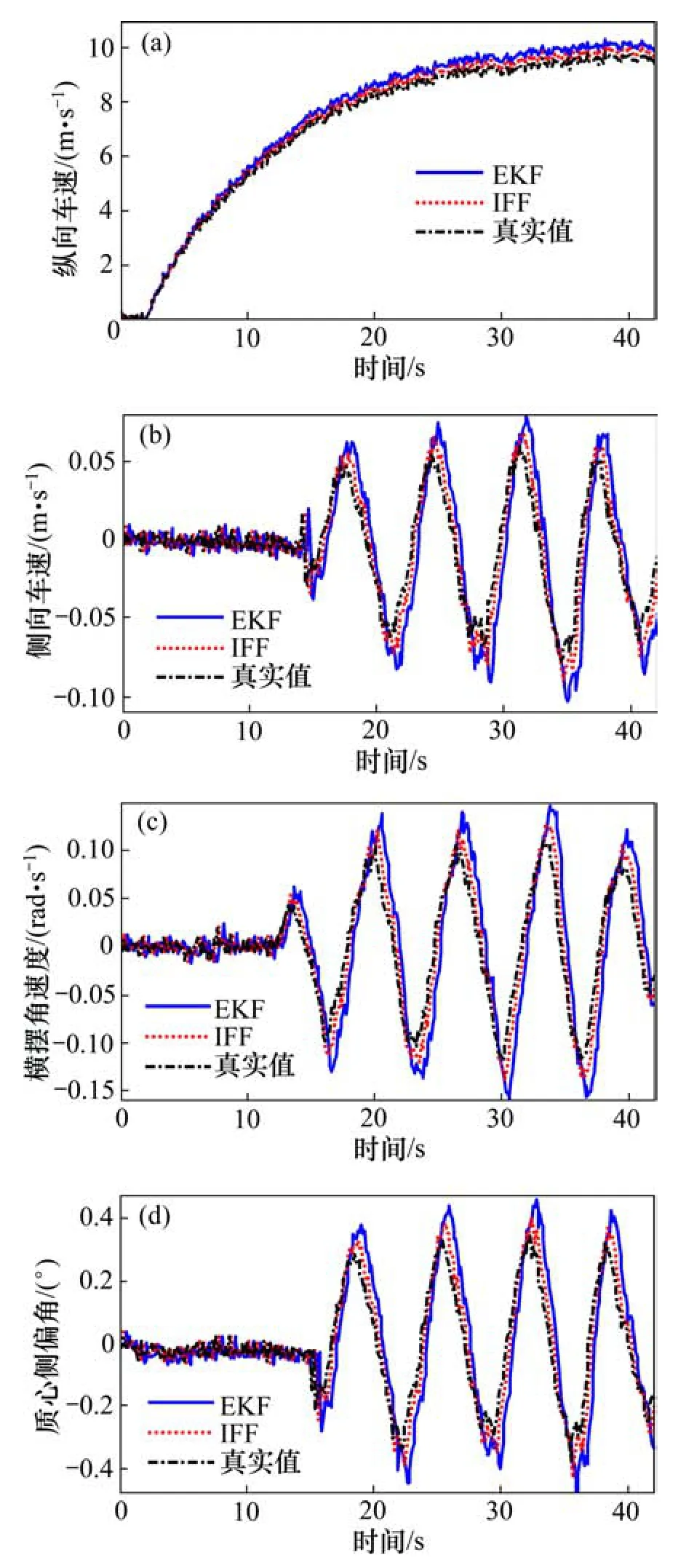
图11 车辆状态估计实验结果Fig.11 Experimental results of vehicle state estimation

6 结论

1) 结合四轮独立驱动电动汽车驱动特点与自身优势，将轮毂电机模型与车轮动力学方程联系起来提出电驱动轮模型，并将其应用到车辆状态估计中，采用低成本传感器进行实时纵向力估计，降低了估计成本，为车辆状态估计提供了新的思路。

2) 基于自适应高阶滑模观测器提出了一种新的纵向力观测器设计方法，能实现电驱动轮模型的未知输入估计。同时，自适应高阶滑模观测器提高了估计的精度与抗干扰能力。

3) 基于信息融合算法提出的车辆状态估计方法将纵向力观测器的估计输出作为已知输入值，能够实现车辆状态的实时估计。IFF相比EKF具有更高的估计精度与更强的实时跟踪能力。