微小圆管和方管中H2/空气燃烧极限的比较与分析

(华中科技大学 能源与动力工程学院，湖北 武汉，430074)

微机电技术由微传感器、微电路、微动力系统等组成[1-2]。传统化学电池体积大、能量密度低，而碳氢化合物燃料的能量密度是传统化学电池的数十倍，且来源充足[3]，因此，微尺度燃烧受到了广泛关注。然而，微小尺度下的燃烧稳定性面临许多挑战。首先，微通道特征尺度缩小导致散热损失比例急剧增大[4]。其次，反应物驻留时间短[5]，燃料中的化学能来不及充分释放，降低火焰温度和燃烧效率。另外，燃烧室的比表面积大，增加了壁面对反应自由基的捕获和销毁力度，导致链式反应终止，带来所谓的壁面淬熄现象[6]。以上几个因素综合起来，使得微小尺度下的火焰稳定极限显著减小。对于笔直微通道内的燃烧来说，影响火焰稳定性的具体因素包括壁面厚度及材料物性[7]、进气速度和预混气当量比[8]、管径或微通道间距[9]等。NORTON 等[7-8]通过数值模拟研究发现壁面厚度和物性参数对于上游热传递(热循环效应)有重要影响；进气速度过小会导致产热过少，散热损失比例增大，过大则减小了反应物驻留时间。WAN等[9]通过实验和模拟指出火焰分裂极限随通道间距增加呈现非单调变化趋势。目前，常用稳燃方法有以下几种：1)热循环。ZHONG等[10]在微型瑞士卷燃烧器中通入甲烷/空气预混气体进行燃烧实验，发现可以减少热损失并加强热循环，稳定火焰燃烧。2) 回流区。刘思远等[11-13]利用钝体和凹腔产生回流区，通过实验和数值模拟证明该方法对微尺度燃烧具有很好的火焰稳定作用；左青松等[14]发现突扩型微通道稳燃能力优于直通道。3) 催化剂。SITZKI等[15]在瑞士卷燃烧器表面附着催化剂，扩大了稳燃范围。除了以上几种主流方法以外，近年来也有不少学者尝试其他稳燃方法，例如，KANG等[16]在预混气体中加入少量H2或CO，抑制了反复熄火、又着火的动态火焰。关于微通道截面形状对于火焰稳定性影响的研究还非常少。为了简化计算，文献[6,9,12-13,16]采用二维模型进行计算。然而，PASHCHENKO[17]通过数值模拟指出，只有当管道长度相对于管径足够大时，二维模型才能得到与三维模型相近的结果。DI BENEDETTO等[18]使用三维模型计算了丙烷在方形和圆形截面微通道内的可燃速度范围，虽然得出了方管稳燃能力优于圆管，但仅解释了两者速度下限因温度分布影响点火阶段的区别，并且只计算了当量比为0.8的工况。为了更好地研究三维模型下微通道截面形状对火焰稳定性的影响，本文作者通过数值模拟方法对水力直径均为1 mm的方管和圆管内 H2/空气火焰的浓度下限和速度极限进行比较研究，并从散热损失和流场特性2个方面进行分析。

1 计算方法

由于微通道的特征尺度对燃烧稳定性起决定性作用，因此，对于不同截面形状的微通道来说，一般控制它们的水力直径保持相等。本文中，2种微通道的横截面如图1所示。方管的横截面边长为1 mm，水力直径也为1 mm，与圆管内径相同(1 mm)。2种微通道的长度均为15 mm，壁厚为1 mm。图1中O1和O2分别为方管和圆管的中心位置，也取为方管和圆管的坐标原点。P1和P2的坐标分别为(0，0.498)和(-0.498，0.498)，分别代表方管内贴近壁面中点处和角落处。P3的坐标为(0.498，π/2)，代表圆管内近壁面处。

图1 圆管和方管的横截面示意图Fig.1 Geometries of channel cross-sections of circular and square tubes

模拟使用的燃料为氢气(H2)，氧化剂为空气(air)。对于实际的燃烧系统，为了保证完全燃烧，一般控制预混气体当量比≤1。微通道壁面材料为耐高温的石英玻璃，其密度、比热容以及热导率分别设置为 2 650 kg/m3，750 J/(kg·K)和 1.05 W/(m·K)，外壁面发射率ε为0.92。进口最大雷诺数(Re)约为500，故采用层流模型。H2/空气的燃烧反应机理采用LI等[19]提出的包含13种组分、19个基元反应的详细机理。基元反应速率采用阿伦尼乌斯形式的有限速率模型。气体混合物符合理想气体状态方程，其热力学参数与动力学参数来自CHEMKIN数据库。

边界条件设置如下：1) 入口采用速度入口条件，预混气温度为300 K。2) 出口采用压力出口。3) 燃烧器的外壁面与环境之间的换热同时考虑自然对流和辐射2种方式，单位面积的散热速率为

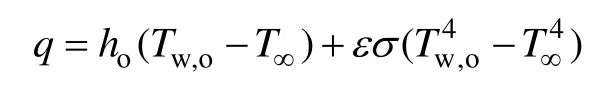
其中：Tw,o为外壁面温度(在迭代过程中，Tw,o用上一轮的值来计算q)；T∞=300 K 为环境温度；σ=5.67×10-8W/(m2·K4)，为 Stephan-Boltzman 常数；ho为自然对流换热系数，因为燃烧器外壁面温度较高，该值比普通情况下略大，取值为 20 W/(m2·K)(假设平均温度为1 000 K进行估算[11])，同时，计算表明，外壁面散热主要通过辐射方式进行，自然对流换热系数对最终的计算结果影响不大。

各方程均采用二阶精度的迎风格式进行离散，采用 SIMPLEC算法来处理压力与速度耦合。模拟使用的CFD软件为Ansys14.0，方形截面、圆形截面均采用四边形网格划分。对不同网格尺寸下的燃烧器进行计算结果独立性验证，以进气速度为6 m/s时的方管作为例子，考察采用不同网格数计算获得的沿中心轴线(Z轴)的温度分布曲线，如图2所示。由图2可见：3种网格数获得的结果差别很小，说明27万网格数已经足达到研究的精度要求，因此，本文最终选择 27万网格数进行模拟，具体来说，长、宽和高方向上的网格长度分别为0.05 mm、0.10 mm和0.10 mm。类似地，对圆管也进行了网格独立性验证，最终选择 31万的网格数进行模拟，其中，轴向网格长度为 0.05 mm、径向网格长度为0.10 mm。

为了验证本文模拟方法的正确性，对文献[20]中的1个实验工况进行数值计算。该工况也采用氢气作燃料，燃烧器通道高度为 2 mm，进气流量为200 mL/min，处于层流工况。因此，用文献[20]中的实验结果来验证本文的模型和计算方法是可信的，二者没有本质上的不同。模拟获得的外壁面温度分布与实验测量值如图3所示。从图3可知：其最大相对误差为6.4%，说明本文结果具有较高的精度。

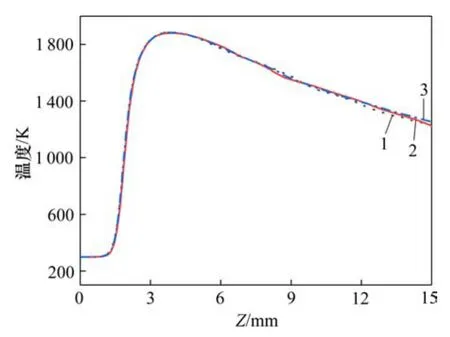
图2 进气速度为6 m/s时，不同网格数计算所得的方管轴线温度分布Fig.2 Axial temperature profiles in square tube at an inlet velocity of 6 m/s for different grid systems

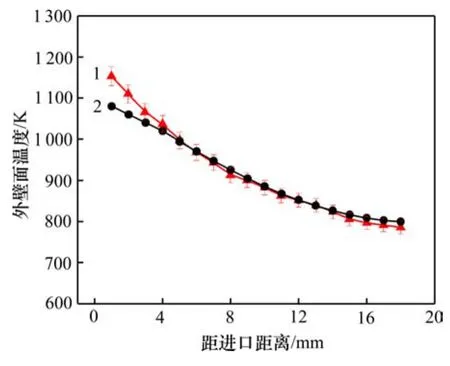
图3 数值模拟方法的实验验证Fig.3 Validation of numerical model

2 结果与分析

2.1 可燃极限比较

对于预混燃烧来说，可燃极限一般包括速度极限和浓度(当量比)极限 2种。速度上限是由于进气速度过大时，反应物停留时间太短，燃烧过程不能充分释放热量，火焰被吹熄。速度下限是由于进气量太小，燃烧过程释放的热量太少，散射损失太大，导致火焰发生熄灭。浓度(当量比)下限的存在是由于燃料浓度太低，燃烧反应释放的热量较少，从而导致火焰熄灭。在计算过程中，首先，基于燃烧理论和经验，对某个工况下的全局模型设定初始高温条件实现点火，经过足够长时间的稳态迭代过程，数值计算收敛，获得该工况下的稳定火焰。然后，逐渐增大进气速度，火焰最终在某个进气速度时被吹熄，该临界进气速度即为速度上限(upper limit)，也称作吹熄极限。类似地，通过逐渐减小进气速度可以得到可燃的速度下限(lower limit)。当量比下限也可以通过类似方法获得。

图4所示为方管与圆管的可燃极限范围。从图4可知：在同一当量比下，方管的速度上限均大于圆管的速度上限，且两者之差保持约为1.7 m/s；方管的速度下限略小于圆管的速度下限，与 DI等[18]的结论相符，因此，方管的可燃速度范围明显比圆管的大；方管在当量比为 0.6时仍能维持稳定燃烧，而对于圆管来说，在该当量比下的任何进气速度，火焰已经无法维持。即方管的可燃浓度范围也比圆管的更宽。可见：在水力直径相同的情况下，微小方管的稳燃能力要比圆管的强，微通道的横截面形状对火焰的稳燃能力有重要影响。

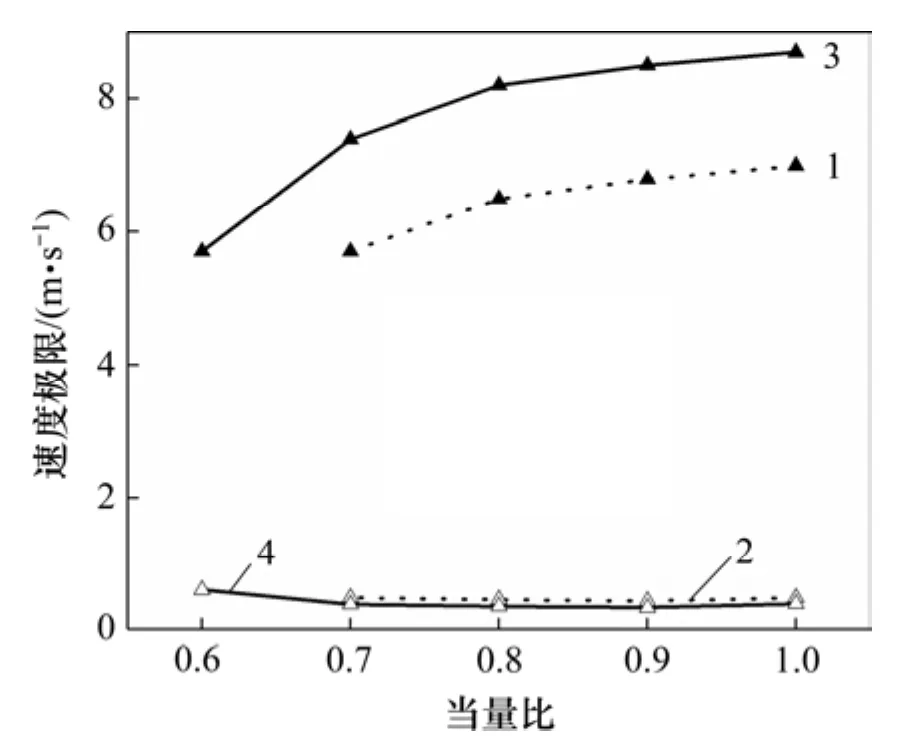
图4 方管与圆管的可燃极限比较Fig.4 Combustible limits of square and circular tubes

为了考察2种微通道的火焰稳定性，图5所示为当当量比为1.0时，方管与圆管内火焰顶部和根部的位置随进气速度的变化。从图5可以看出火焰在2种微通道中的不同移动规律。需要指出的是，由于方管是周向不对称的，其火焰根部的位置沿周向并不完全相同，因此，图5中同时给出了2个特征点(P1和P2)的火焰根部位置。而圆管则是周向对称的结构，因此，图5中只给出了1个点(P3)的火焰根部位置。

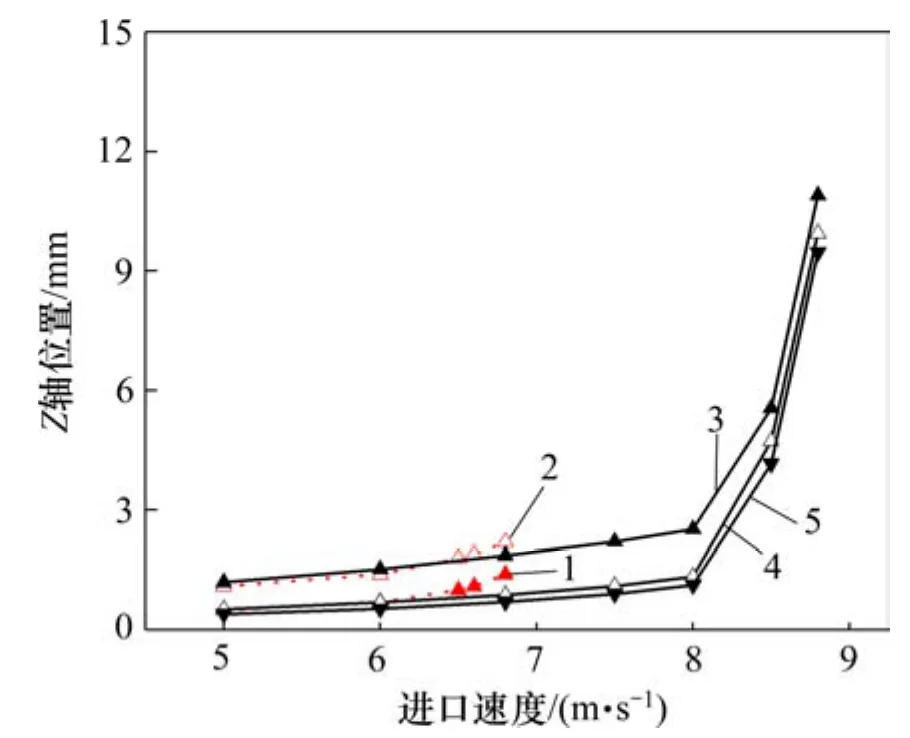
图5 当量比为1.0时，方管与圆管火焰顶部、根部位置随速度的变化Fig.5 Variation of flame position with increasing inlet velocity in square and circular tubes at equivalence ratio of 1.0

从图5可知2种微通道中不同的火焰移动规律。首先，当进气速度较低时，火焰在2个微通道内的位置相近，均位于上游靠近进口处。其次，圆管内的火焰在临近速度上限时的位置与低速下并没有显著差别，当进气速度增大到6.9 m/s时，火焰突然被吹出管外；而方管在临近速度上限时，火焰位置向下游发生明显移动，直至速度达到8.7 m/s时被吹熄，此时火焰已接近管口。另外，方管角落处的火焰位置(P2)相对于横截面边长中点处(P1)的火焰尾部位置来说略靠上游，说明方管的4个角落使得火焰具有明显的三维特性，同时也能提高火焰的稳定性，增大速度上限。

2.2 结果分析

对于没有钝体等稳焰器的直通道来说，其主要稳燃机制是基于边界层，而导致火焰失稳的主要因素是通过外壁面的散热损失和火焰顶部的拉伸效应。下面以当量比为1.0、进气速度为5 m/s的工况作为例子，从散热损失比例、流场特性以及火焰拉伸效应等几个方面对方管和圆管的稳燃能力之间的差别进行比较和分析。

2.2.1 散热损失

前面已经指出，散射损失比例增大是影响微尺度燃烧稳定性的首要因素。散热损失比例(heat loss ratio)一般定义为通过微通道外壁面的散热量与燃烧过程释放的总热量的比值。数值模拟完成后，可通过FLUENT软件导出相关数据，计算得到该工况下方管与圆管的总产热量分别为14.43 W和11.11 W，散热量分别为10.39 W和8.34 W，计算得到方管的散热损失比例为0.72，而圆管则为0.75，如图6所示。对于水力直径均为1 mm的方管与圆管，计算表明二者的面/体比完全相等，均为4 000 m-1，但从图6可知方管的散热损失比例略小于圆管的散热损失比例。由于壁面散热是影响微尺度燃烧的1个重要因素，特别是火焰接近可燃极限时。因此，采用方管可以稍微减小散热量，从而有利于火焰稳定。

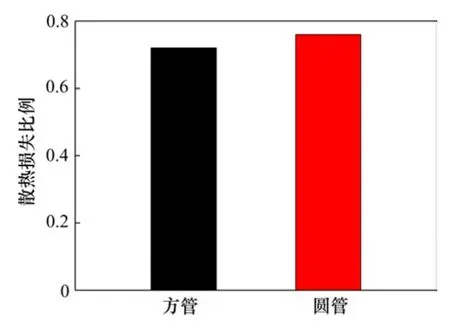
图6 散热损失比例Fig.6 Heat loss ratio

2.2.2 流场特性

虽然方管和圆管的水力直径均为1.00 mm，但是方管的横截面周长为4.00 mm，而圆管只有3.14 mm，前者是后者的1.27倍，即在方管内稳定火焰根部的边界层周长比圆管更长，并且在方管角落处存在低速区，因此，方管对火焰根部有更好的拖拽作用。图7所示为方、圆管中火焰锋面上的速度云图。从图7可以看出：方管在角落处的火焰位置相对于壁面中点处更加靠近上游，而圆管内的火焰根部则对称地分布于同一平面。图8所示为近壁面 3个特征点处(P1，P2，P3)沿流动方向(Z轴)速度分布。由图8可见：方管四周中点处(P1)的贴壁速度最大值要比圆管近壁面处(P3)的小，分别为0.46 m/s和0.54 m/s。尤为重要的是，方管角落处速度几乎为0，说明方管角落处边界层较厚，始终存在1个速度极低的流体层，更加有利于火焰根部的稳定，这就是图7中方管角落处火焰根部更加靠近上游的原因，也是方管比圆管拥有更大速度上限的重要原因之一。

图7 火焰锋面上速度分布Fig.7 Velocity in flame fronts

图8 进气速度为5 m/s时，方管和圆管近壁面处沿流动方向的速度分布Fig.8 Longitudinal velocity profiles near walls of square and circular tubes at inlet velocity of 5 m/s

OH基团可用来表征燃烧反应过程的强度。图9所示为近壁面2个特征点处(P1，P3)沿流动方向(Z轴)的OH基团分布。从图9可以看出：方管四周中点处(P1)的近壁面 OH浓度峰值和高浓度区均比圆管近壁面处(P3)的宽，说明方管在近壁面处反应强度要比圆管的大，有利于火焰稳定。

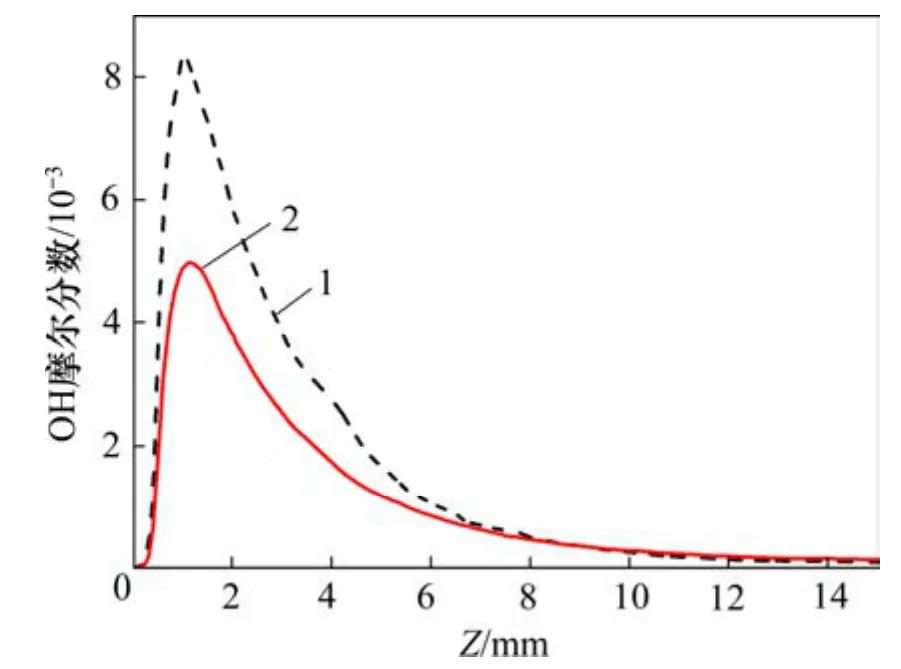
图9 进气速度为5 m/s时，方管和圆管近壁面处沿流动方向的OH摩尔分数分布Fig.9 Longitudinal profiles of OH mole fraction near walls of square and circular tubes at inlet velocity of 5 m/s

2.2.3 火焰拉伸效应

影响微通道稳燃能力的另一个重要因素为火焰顶部的拉伸效应，这里主要从应变率(strain rate，数据可从FLUNET软件导出)来进行比较。图10所示为当进气速度为5 m/s时，方管和圆管沿中心轴线的应变率分布。从图10可见：圆管内火焰顶部的应变率要比方管的大许多，分别为78 411 s-1和62 405 s-1。因此，火焰在圆管内受到的拉伸效应比方管内的更强烈，不利于火焰稳定。

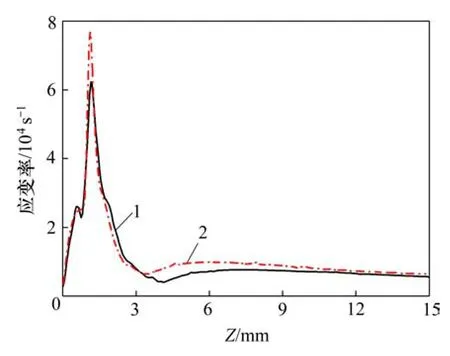
图10 进气速度为5 m/s时，方管和圆管沿中心轴线的应变率分布Fig.10 Longitudinal profile of strain rate in square and circular tubes at inlet velocity of 5 m/s

3 结论

1) 通过数值模拟方法获得了相同水力直径(1 mm)的方管和圆管内氢气/空气火焰的可燃浓度极限和速度极限。

2) 方管的可燃浓度范围和速度范围比圆管的都要宽，即稳燃能力更强。这主要有3个方面的原因：① 方管的散热损失比例比圆管的略小；② 方管的截面周长比圆管的更大，火焰根部更长，尤其是4个角落存在速度极低的稳燃区；③ 方管内火焰顶部的应变率比圆管的更小，火焰受到的拉伸效应更弱。这3方面的因素综合起来，使得方管具有更强的稳燃能力。