水流条件下单点系泊不同结构“钻石型” 重力式网箱的水动力特性数值模拟❋

程 晖, 黄六一, 倪 益, 董双林, 赵芬芳

(中国海洋大学水产学院，山东 青岛 266003)

目前我国近岸海水养殖已经基本饱和，随着沿海各地对环境和生态保护要求的提高，近岸养殖空间将进一步压缩，海洋水产品产量很难有较大提高，需要进一步拓展海水养殖空间[1]。因此，积极发展深远海网箱养殖已成为我国海洋渔业空间拓展的必然选择。近年来，利用黄海冷水团进行冷水性鱼类的离岸网箱养殖成为海水养殖的一个热点。黄海冷水团绿色高效养鱼项目已经列入山东省“海上粮仓”建设计划重点项目和青岛海洋科学与技术国家实验室重大科研任务预研项目[2]。养殖网箱是在黄海冷水团开展冷水性高品质鱼类绿色养殖的最重要载体，开发安全、智能化新型网箱是建成冷水团鱼类养殖基地的重要保障。

由于抗风浪网箱常年投放在海中，海上波浪、海流及台风的恶劣海况，很容易引起网箱的大变形，甚至网箱的结构破碎[4]。虽然海水养殖网箱至今已有几十年的发展，其结构的安全性、可靠性依然是制约网箱往深远海方向发展的主要因素。一方面海流引起网箱变形会减少其有效的养殖容积，增大养殖鱼类所受的环境压力，影响其生长；另一方面，波浪引起网箱框架不断摆动，容易导致框架的结构疲劳以及结构连接件的破碎。特别是深水离岸网箱的研究历史较短，还有较多问题需要深入研究。

对网箱这种柔性结构的水动力学研究主要有两种方法：模型实验和数值模拟。随着计算机硬件的升级和算法的改进，目前数值模拟方法越来越多的应用于网箱设计中。朱立新[3]、何鑫[4]在Matlab编程环境下利用有限单元法对重力式网箱群在水流下的形变进行了研究。赵云鹏[5-8]在Fortran编程环境中利用质量集中法建立数学模型，对网衣和重力式网箱在波流下的形变进行了研究。胡保有[9]和高晓芳[10]利用Matlab 中的Simulink工具进行可视化编程来分析网箱在波浪作用下的位移。崔勇[11-15]利用ANSYS中的命令流对方型金属网箱进行了波流状态下的形变、锚泊受力的研究。张福友[16]利用了经典ANSYS中的PIPE59+LINK16单元来模拟网箱在水流下的变形，并与实验进行对比，并提出刚性配重的网箱水平漂移要小于重锤形式的网箱。王笛清[17]利用了ANSYS中的结构分析模块对网箱的浮框进行了力学特性分析。李鲤[18]用ABAQUS研究了波流状态下的深海浮式网箱结构动力响应，并得出了在规则波和不规则波下网箱结构动力响应。Trygve Kristiansen[22-23]提出使用网面单元和杆单元对网箱进行数值模拟，Chang[24]使用Abaqus 对全尺寸网箱在波流下的变形进行了研究，Ida[25]利用实验数据对FhSim和FishSim两种网箱模拟软件进行验证，结果显示两个软件在水流速度0.5 m/s以内的结果十分吻合，当流速超过0.7 m/s或者波陡超过1/15时数值模拟的阻力会过大。

本研究采用数值模拟方法，对目前在黄海冷水团使用的“钻石型”单点系泊网箱设计5种不同结构，进行网箱水动力特性数值模拟，分析网箱不同箱体结构的中部水平漂移、底部水平漂移和阻力等特性，获得该网箱较优箱体结构，为该类型网箱的结构设计提供技术支撑。

1 材料与方法

1.1 方法原理

数值模拟使用有限元方法，在计算中对网线材料、水流等做以下假设：

(1) 网线绝对柔软，只能承受轴向拉力；

(2) 网线单元拉伸前后的横截面积保持不变；

(3) 根据中村充[27]重力式网箱网内流速公式，水流经过网片后流速衰减8.5%。

网箱结构动力学计算核心是根据虚功原理来求解经过时间和空间离散后的运动方程(见公式1)。

(1)

(2)

(3)

(4)

1.2 试验方案

1.2.1 网箱模型
图1为本文研究的单点系泊网箱原型。该网箱系统包括浮框、底框、箱体、浮子、锚绳以及锚。本文为研究锚泊缆绳受力，将网箱框架设置固定在水面。由于只受水流影响，试验采用田内准则[28]，实物网箱与模型网箱大尺度比为40，小尺度比为3，数值模拟的模型网箱与原型网箱的参数见表1。本文使用的数值模拟方法已经通过水槽模型试验验证[19]，验证结果显示数值计算的阻力与实验所得阻力平均误差13.5%，水平漂移平均误差为5.69%。

图1 单点系泊网箱结构示意图

组件Component参数Parameter模型网箱Model scale原型网箱Full scale浮框Floating system内浮框周长Circumference of inner pipe/m1.560外浮框周长Circumference of outer pipe/m2.1184.4浮管直径Outer diameter of pipe/mm8315浮管厚度Pipe thickness/mm117网衣Netting system网目大小Mesh size/mm1030网线直径Twine diameter/mm13网箱高度Height/m0.87535沉框Sinker system重量Weight/kg0.176450沉框管直径Outer diameter/mm3110

1.2.2 方案设置 根据以往的设计经验和相关参考文献可知，网箱的水平漂移与网箱配重的大小、配重的位置、配重的形式(刚性或柔性)、网箱底框形状、网目形状、网箱网袋锥度有关[3-6]。根据上述资料设置表2所示的5种方案进行数值模拟，并将计算结果与文献[19]中网箱(以下简称方案0)进行比较。

表2 优化方案参数表

方案1与方案0相比，箱体从网高的1/2处开始由上半部分的六边形变为圆形， 圆柱形网衣相对于六边形网衣在90°夹角时迎流面积较小，水流载荷较小，有利于减少水阻力。

方案2与方案0相比，网衣方形网目改为菱形网目，其他条件不变，菱形网目和方形网目是常用的网箱网目形状，根据以往的研究，菱形网目网衣可以减少网箱水平位移，但是会导致网箱网底倾斜和偏转[11]。

方案3与方案0相比，改变了网箱的配重方式，在保证总配重不变的情况下，将一半的配重以6个重锤的方式加载到网体的中间位置，并且在箱体中间位置增加一个刚性圆环，圆环的密度与水相同，箱体中间增加刚性圆环可以有效地保持网箱箱体在水流中的体积，但同时会增加迎流面积，增加水流载荷；箱体中间增加配重有利于保持箱体形状。

方案4与方案1相比，在箱体中间位置增加一个刚性圆环，同时将底框形状变为圆形，这样能够较好的控制网箱的水平位移，但是由于迎流面的增大，会导致网箱阻力增大。

方案5与方案1相比，将箱体改为上大下小的圆台型，箱体锥度为0.9，并且在中间加一刚性圆环，在低流速条件下圆柱形网箱有较大的初始变形，容积损失率较大，而圆台形网箱初始变形很小，容积损失率较小，具有较好的耐流特性和抗变形能力。

1.2.3试验工况 根据实际海流的情况，以及文献[19]中的计算条件，本文数值模拟实验中使用的水流速度如表3所示。

表3 实验流速设置

1.3 数据处理

本研究使用田内准则进行数值模拟实验，来计算模型网箱在纯水流作用时的阻力和变形。田内准则的比例关系如下：

(5)

(6)

(7)

式中：lp、lm分别为原型和模型的主线尺度；下标p代表原型；下标m代表模型；ap、am分别为原型网和模型网的网目目脚长度；dp、dm分别为原型网和模型网的网线直径；vp、vm为实际和模拟流速。数值模拟实验中大比例尺λ设置为40，小比例尺λ′为3。根据田内准则对模拟实验数据进行换算，获得出实际网箱的阻力(公式8)和网箱的水平漂移(公式9)。

Fp=Fm×λ2×λ′。

(8)

Xp=Xm×λ。

(9)

在本研究中，网箱中部水平漂移是指网箱背流面网衣的中心位置在来流方向上的位移变化，网箱底部水平漂移是指网箱底框最后沿位置在来流方向上的位移变化。

2 结果

2.1 箱体形状

图2为各优化方案在实际流速1 m/s时的形状变化结果。图中利用俯视图、侧视图和正视图显示网箱箱体在受到水流作用时的变化情况。从图2中可以看出仅改变底框形状对网箱的变形影响并不明显(对比方案1)。网目形状的改变对网箱变形有较大的影响(对比方案2)，菱形网目的网箱由于网线结构为斜向交叉结构，在重力作用下会有网箱中部向内收缩的趋势 (图2方案2正视图)，并且在水流冲击时网箱的底部后方会明显抬起，这些现象与崔勇[14]、赵云鹏[6]所做的数值模拟有相似的结论。将配重的位置提高在一定程度上可以降低网箱中部的水平漂移，但是网箱的底部漂移会更大(对比方案3)，因此在总配重一定的情况下，将所有配重集中到网箱底部是最佳分配方式。方案4和方案5均是在中间增加了一个固定环，通过增加刚性的圆圈，可以减小网箱的容积损失和水平漂移。

2.2 网体中部水平位移

各优化方案的箱体中点水平位移计算结果与方案0网箱的比较见图3和表4。表4中网箱位移为换算后的实际位移，变动率为优化方案相对于方案0网箱水平位移变化率。从图3中可以看出随着水流速度增大，网箱中点处的水平偏移量随着增大，增大的速度随着水流速增大而减小。所有的优化结果中部的水平漂移均比方案0网箱的小，其中效果最好的为方案5，其次分别为方案2、方案3、方案4、方案1。当水流速度为1 m/s时，与方案0网箱相比方案5网箱中部的水平漂移减少30.59%。

2.3 箱体底部水平位移

各优化方案的网箱底部位移计算结果与方案0网箱的比较见图4和表5。从图4中可以看出所有的优化结果的在网箱底部的水平漂移均比方案0网箱的小。但是这种差别随着流速的增大而减少。其中效果最好的为方案2，其次为方案5，方案3，方案4，方案1。当水流速度为1 m/s时，与方案0网箱相比方案2网箱底部的水平漂移减少37%，案5网箱底部的水平漂移减少22%。

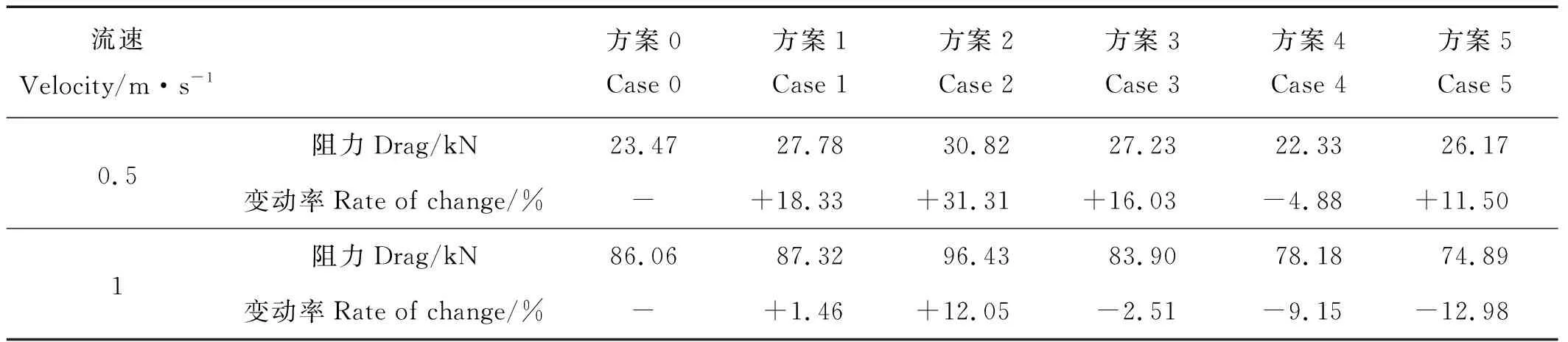
2.4 网箱总阻力优化

优化方案的阻力计算结果与方案0网箱的比较见图5和表6。图5中可以看出网箱阻力随着水流速度的增大而增大。优化方案1、2比方案0网箱的阻力稍大一些，优化方案3的阻力结果与方案0网箱相当，优化方案4、5比方案0网箱的阻力小。当流速为1 m/s时，优化方案5的阻力最小，与方案0网箱相比的阻力小13%，这是因为采用的是圆锥形网衣，在来流方向的投影面积小于其他各种方案。

图2 流速为1 m/s时各优化方案位移云图

图3 网箱中部水平位移结构优化结果

流速Velocity/m·s-1方案0Case 0方案1 Case 1 方案2 Case 2 方案3 Case 3方案4Case 4 方案5 Case 50.5水平位移X-displacement/m10.918.538.5668.568.526.96变动率Rate of change/%--21.79-19.81-21.52-21.88-36.211水平位移X-displacement/m12.0010.679.5810.4410.778.34变动率Rate of change/%--11.18-20.23-12.98-10.34-30.59

图4 网箱底部水平位移结构优化结果

流速Velocity/m·s-1方案0Case 0方案1 Case 1 方案2 Case 2 方案3 Case 3方案4Case 4 方案5 Case 50.5水平位移X-displacement/m20.4618.0912.4617.5114.6014.45变动率Rate of change/%--11.54-39.08-14.44-28.62-29.351水平位移X-displacement/m23.2121.7314.5521.2321.1318.02变动率Rate of change/%--6.39-37.33-8.53-8.99-22.39

图5 网箱阻力计算结果

流速Velocity/m·s-1方案0Case 0方案1 Case 1 方案2 Case 2 方案3 Case 3方案4Case 4 方案5 Case 50.5阻力Drag/kN23.4727.7830.8227.2322.3326.17变动率Rate of change/%-+18.33+31.31+16.03-4.88+11.501阻力Drag/kN86.0687.3296.4383.9078.1874.89变动率Rate of change/%-+1.46+12.05-2.51-9.15-12.98

3 讨论

表7为上述优化方案结果汇总。优化方案计算结果以及其与原型网箱相比的变化值，“+”代表增大，“-”代表减少。综合优化方案与模型网箱的水平比较可以发现方案5为所有优化方案中最好的，网箱的阻力减少的同时，网箱中部和底部的位移均有较大的减小。据此可以建议将网箱箱体设计为上大下小的形状、采用方形网目、在网箱中间加抗变形的圆环和将配重集中在底部可减小网箱水平漂移和阻力。

Note：①Full-scaled velocity is 0.5 m/s；②Full-scaled velocity is 1.0 m/s；③Case No.；④Displacement at the middle；⑤Displacement at the bottom；⑥Drag force；⑦Case 0；⑧Case 1；⑨Case2；⑩Case3；Case 4；Case 5

3.1 流速对各方案水平位移的影响

通过对各个方案的比较可以看出，优化方案可以在一定程度上降低网箱的水平位移。当流速增加时，网箱的水平漂移均增大；网箱水平漂移的增长速度会随着水流速度增加而降低，呈对数函数增长关系，这与崔勇[11]、张福友[16]研究结果相似。当实际流速度超过0.6m/s时除优化方案2和方案5外，其他优化方案与方案0的网箱在水平位移方面差别较小。

3.2 网目形状对水平位移和总阻力影响

通过方案2与方案0网箱相比可以看出，菱形网目的网体可较大幅度的减小网箱水平位移，但是所带来的网箱底框的大幅度倾斜和偏转，会增大箱体的不稳定性。菱形网目在重力作用下由于网片自身张力作用会使网目减小，增加了网片的密实度，增加水阻力。崔勇[11]研究发现在低流速下两者差异不明显，而在中高流速下，方形网目网箱迎流面缆绳张力大于菱形网目网箱，其网箱运动幅度大于菱形网目网箱。结合网体中部的位移结果和网体的水平位移云图，与其它采用方形网目箱体比较发现方案2的位移规律与其他形状的网箱有较大的不同，其网体中部的水平位移在低流速时较小，但是随着水流速度增大而快速增大，这与崔勇[11]研究结果相似。究其原因，可能是由于其菱形网目局部网线受力传递不如方形网目均匀所致。根据位移云图所示，方案二的网体在水流下底框倾斜很大，背流侧部分的网衣几乎与水面平行，当实际流速为1 m/s时，其网体形状呈反“7”形状。

3.3 配重形式对水平位移和总阻力影响

通过优化方案3与方案0网箱相比，在保持总配重重量不变的情况下，配重集中在底部比配重分散到网箱不同网高处更有利于网箱的形状保持。张福友等[16]研究了在相同配重重量下底层均匀配置沉子、底层和中间均匀配置沉子、最底层配置底圈3种方案的耐流特性，发现最底圈配置底圈网箱水平位移最小，其次为底层和中间均匀配置沉子网箱。从结构力学的角度来考虑，将浮框视为固定点，配重距浮框越远，提供的回复力矩越大。因此最经济的配重分布应该加载到网箱的最底端，而不是网箱的其他部位。

3.4 刚性圆环对水平位移和总阻力影响

优化方案4与方案1网箱相比，在网箱中部合适的位置增加刚性圆环能够较好的控制网箱的水平位移。水流的冲击会使网衣向后倾斜，向后倾斜的程度与水流荷载的大小有关。由于网箱迎流面网衣对水流的衰减作用，网箱背侧的网衣受到的水流的荷载要更小一些，因此向后倾斜的角度会小。增加一个刚性圆环，将前后侧网衣连接起来，能够在一定程度上控制网箱的水平移动。增加的抗变形圆环可以采用与水密度相似的硬质塑料管，从而在不增加网箱的浮力储备的情况下，减小网箱的水平位移。

3.5 箱体形状对水平位移和总阻力影响

通过方案1和方案0的结果对比看出，圆形网箱比六边形网箱有着更小的水平位移。圆形的底框和圆形的网衣有利于减少阻力和水平位移，这是因为六边形网衣的90°夹角迎流面积大于圆柱形网箱，水流作用在网衣上面的作用力比较大。圆柱形的网衣与来流方向成90°夹角的面积小，因此网衣所受的水流荷载要小于六边形网箱的网衣。根据方案5和方案4的对比可以看出上大下小的圆台型网箱水平漂移距离更小。黄小华[26]研究发现在低流速条件下圆柱形网箱有较大的初始变形，容积损失率较大，而圆台形网箱初始变形很小，容积损失率较小，具有较好的耐流特性和抗变形能力，与本实验结果相似。从阻力角度来看，将六边形箱体换成圆形的箱体有利于减少阻力。对比方案4和方案5 可以看出圆台形箱体由于迎流面积减少，其阻力会更小。当来流速度小于0.5 m/s时，方案5的阻力要比方案4增大，这可能与网箱周围的流场效应有关系，需要做进一步的研究来探索这一现象。

4 结语

网箱箱体变形是网衣水阻力与网箱配重重力的平衡结果。如果采取措施使箱体减少变形，网箱的网衣迎流面积会相对较大，此时网箱阻力会增加。如果在保持大的养殖容积和减少网箱阻力两者中只能选一个，应首先选择保证网箱的养殖容积，这是网箱养殖目的决定的。研究结果表明，采用刚性底框、方形网目，中部增加刚性圆环，网体形状为上大下小的圆台形，有利于减小网箱的横向位移，增大网箱养殖容积。