集装箱进出口码头泊位-堆场协同分配的动态决策

韩笑乐， 鞠留红， 钱丽娜， 陆志强

(同济大学 机械与能源工程学院， 上海 201804)

随着海上运输业的快速发展，集装箱码头在全球物流业中的作用越来越重要.码头中泊位和堆场等核心资源的有效分配已成为提升其服务水平的关键.现有文献大多将泊位和堆场视为相互独立的资源进行研究[1-2]，而在码头的实际运营过程中，泊位与堆场间存在相互联系和相互制约的关系，因此，近年来不少研究者开始考虑泊位与堆场资源的协同作用[3-4].另一方面，在码头的实际运营过程中还存在各种不确定性因素，其中船舶到港时间是最普遍的不可控因素[5-6]，其会导致码头作业无法准确安排、资源无法合理利用和船舶到港时间延长.Moorthy等[5]针对船舶到港时间的不确定性，将泊位分配问题与堆场问题相结合，运用模拟退火算法进行求解；Xu等[7]和Zhen等[8]在研究泊位分配问题的过程中考虑了船舶到港时间与作业时间的不确定因素；Zhen[9]在对转运港的堆场模板进行求解的过程中考虑了时间与空间的不确定性，包括泊位位置以及在泊时间；Xiang等[10]针对到港时间及作业时间不确定条件下的泊位分配问题，考虑经济效用及客户满意度，并采用自适应灰狼算法进行求解；Schepler等[11]以多终端、多模式海运集装箱码头为研究对象建立了双目标模型，以最小化集装箱码头的运输时间及船舶到港时间，并采用基于混合整数规划分解的启发式算法进行滚动求解；Zhen[12]从海运市场的不确定性出发，针对到港船舶装、卸载量的波动，研究了码头核心资源的有效分配.在干扰环境下，为了最小化与原调度方案的偏差，Zeng等[6]采用岸桥重调度、泊位重分配的方法解决突发的干扰问题，采用局部重搜索与禁忌搜索相结合的算法进行求解；Liu等[13]将干扰恢复的重调度问题分为泊位位置、靠泊时间以及岸桥数量的分配和对每个岸桥具体调度的问题.

总之，针对不确定环境下的决策有2种方式，即前摄-反应式[8]与滚动周期式[14].前摄-反应式决策预先考虑不确定性因素，注重相对较长决策期间内决策的鲁棒性；而滚动周期式决策是利用最新的信息在较短决策期间内进行滚动决策，具有更强的灵活性.区别于现有文献，本文主要针对集装箱进出口码头的泊位-堆场资源的协同分配，并兼顾决策的鲁棒性与灵活性，借鉴针对复杂多阶段随机优化过程、基于两阶段近似的决策框架[15]，将第1阶段固定性决策与第2阶段各场景下的可调整决策进行区分与结合，提出了定制化的动态决策方法，并验证其有效性.

1 问题建模与分析

1.1 泊位-堆场资源的协同分配模型

图1 泊位-堆场资源分配的相互关系Fig.1 Interrelationship of berth allocation and yard allocation

目标函数为

(1)

约束条件分别为

si≤txit+M(1-xit), ∀i∈V,t∈T

(2)

ei≥txit, ∀i∈V,t∈T

(3)

(4)

(5)

(6)

(7)

fi=Ai-TL, ∀i∈V,t∈T

(8)

gi=ei+TD, ∀i∈V,t∈T

(9)

(10)

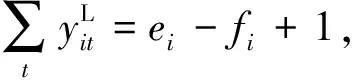
(11)

(12)

bi≤jwij+M(1-wij), ∀i∈V,j∈J

(13)

bi+Li-1≥jwij, ∀i∈V,j∈J

(14)

(15)

(xit+wij-1)/2≤αijt≤(xit+wij)/2

(16)

∀i∈V,j∈J,t∈T

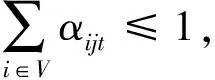
(17)

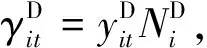
(18)

(19)

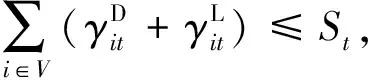
(20)

(21)

si,ei∈{Ai,Ai-1,…,T}, ∀i∈V

(22)

fi∈{-TL,TL,…,0,…,T}, ∀i∈V

(23)

gi∈{Ai,Ai-1,…,T}, ∀i∈V

(24)

bi∈{1,2,…,J-Li+1}, ∀i∈V

(25)

(26)

∀i∈V,j∈J,t∈T

目标函数(式(1))以常用的船舶总在港时间为衡量标准.式(2)～(9)定义了与船i相关的各时间决策变量，并限定其相互关系；式(10)～(12)确保了船舶及其集装箱在港时段的连续性；式(13)～(15)定义了船i的靠泊位置决策，并确保了占用泊位区段的连续性；式(16)～(17)基于xit、wij定义了αijt，并且确保任意时段泊位区段的被占用量上限为1；式(18)～(20)基于船舶在港定义了堆场资源占用量，并确保任意时段的堆场被占用量不超过其上限；式(21)确保了各船的累计作业量满足集装箱装卸需求；式(22)～(26)为决策变量的定义域.

1.2 动态性分析与船舶分类

在信息层面，码头和船运公司对于到港时间预估的准确性会随时间的推移而逐渐提高.船舶的真实到达时间通常能够提前1 d获得；而距离更远的船舶则只能预估到港时间的期望值，其随机分布信息可以由场景ω描述.

在操作层面，所提出的动态决策方法是基于滚动周期机制并以1 d作为决策点的间隔的.定义周期K是从决策点k到决策点k+1的时间段.一方面，在任意周期K开始时，该周期内的到港船舶都已经确认到港时间，周期K以外的后续船舶到港时间尚不确定；而在周期K结束时，周期K+1内的到港船舶都将确认到港时间，依次类推.在一个决策周期内，新的信息将不断被确认，但已决策的计划不会被立即修改，而必须等到下一个决策点再次更新决策.另一方面，对于已经离港但其进口箱仍留存在堆场，以及尚未到港但其出口箱已预存堆场的船舶，其到港时间不属于当前周期，但仍会影响当前周期内的堆场占用决策.

基于上述动态性分析，在各个滚动决策点k上，将待决策船舶分为3类，其信息和操作特性表述如下：

(1) A类.在决策点k已经开始但未完成作业，包括某些在周期K-1前到港和在周期K-1内到港.A类船舶不需要进行决策，直接按照已有计划继续作业.

(2) B类.在决策点k尚未开始作业但会在周期K内到达.对B类船舶引入0或1的决策变量ui作为延迟判定因子，因其中某些船会在周期K内开始作业(ui=1，归入B1子类)，某些船会延迟到下一周期重新做出决策(ui=0，归入B0子类).B0类船舶需要决策其资源分配并予以执行，而B1类船舶则与C类船舶进行同样操作.

(3) C类.在周期K+1至K+[TL/24 h]内到达.C类船舶与B1类船舶一起可决策场景ω下的资源分配，但其在周期K内不需要执行，并保留在周期K+1内调整的权利.

2 决策框架与优化算法

2.1 基于两阶段近似的动态决策框架

各决策点k的两阶段近似优化模型的逻辑架构如图2所示.其中，将现有参数作为第1阶段的确定信息和第2阶段不确定场景下的随机参数.在决策对象中，第1阶段的固定性决策ξk需要在本周期内执行，而第2阶段的可调整决策ξk+1,ω用于辅助评估第1阶段决策的预决策，不需要在本周期内执行，后续周期随着信息的不断更新而确认，仍可做出相应地调整.因此，决策点k的目标函数也包括了第1阶段的固定成本z(ξk)，以及第2阶段各场景下可调整成本的期望值EΩ[z(ξk+1,ω|ξk)].

图2 两阶段近似优化模型的逻辑架构Fig.2 Logic structure of two-stage approximation model

目标函数沿用式(1)的船舶总在港时间，但综合第1阶段的固定性时间以及第2阶段各场景下的可调整期望时间，即

(27)

约束条件的数学表述可通过泊位-堆场资源协同分配模型的约束在各场景ω下扩充得到.另外，对于A类船舶和决策所得的B0类船舶，还需增加以下约束，以确保各场景下决策的一致性：

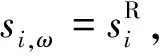
(28)

(29)

(30)

-Mui≤si,ω-si,1≤Mui

(31)

∀i∈VB,ω∈Ω

M(ui-1)≤si,ω-Tk+1≤Mui

(32)

∀i∈VB,ω∈Ω

-Mui≤bi,ω-bi,1≤Mui

(33)

∀i∈VB,ω∈Ω

2.2 各决策点的两阶段禁忌搜索

由于各决策点的两阶段近似优化模型包含随机场景，在实际算例规模下很难使用商用求解软件(如Cplex软件)直接求解，所以本文基于图2的逻辑架构提出两阶段禁忌搜索(TS)算法，其框架如图3所示.其中，外层TS1和内层TS2(ω)分别搜索第1阶段的固定性决策ξk和第2阶段各场景ω下的可调整决策ξk+1,ω.在编码和搜索中，均采用待决策船舶优先级来编码；邻域生成通过互换(Swap)操作进行，禁忌对象为上一步移动的互换操作，禁忌次数在禁忌上限与禁忌下限之间随机生成，并循环进行禁忌搜索直至最大循环次数.在解码和评价中，均采用首个适合(First fit)的解码方式，按照当前优先级的顺序，依次为船舶分配最早可用的资源；以TS1层的当前决策作为TS2(ω)层的输入，TS2(ω)层的当前决策则用于TS1层的评价.

在解码过程中，B类船舶自然地被划分为2类：若能够在当前决策周期内安排并开始作业，则为B0类；否则，将被延迟到下一个周期重新决策，即为B1类.这种分类作为第1阶段的固定性决策，是在解码过程中自然区分的.相较于显式指定类别，这种隐式指定降低了不可行解或较差解出现的可能性.若指定太多的B0类船舶，则部分B0类船舶可能无法被安排在周期K而造成不可行解；反之，则可能导致周期K的资源利用不足与浪费.

3 数值实验与结果

本文基于Zhen等[16]研究中的参数配置生成随机算例.生成小、中、大3种问题规模，对应的每周到港船舶数V分别为20、30、40.考虑到进、出口港与中转港运营的差异性，设置堆场的名义利用率约为50%，即小、中、大问题规模下的堆场容量分别为 27 000、39 000、54 000 TEU，并设置各船的进口箱占比服从均匀分布，即U[0.2,0.8].

按照本文所提出的动态决策框架依次进行连续7个周期的决策.其中，C类船舶的到港时间延迟量服从分布U[0,10] h，依此生成样本规模为30的场景池，即|Ω|=30；船舶真实到港时间独立于所生成的场景.在小、中、大问题规模下，分别生成10个随机算例.对于每个算例，设计如下4个对比实验：

实验1(Cplex软件) 在确定性环境下，基于完全后验信息，使用Cplex软件单次求解第1阶段优化模型，包含7个周期.

实验2(禁忌搜索) 在确定性环境下，基于完全后验信息，使用简化的动态决策框架，即单次求解两阶段近似优化模型，其中两阶段禁忌搜索的第1、第2阶段决策区间分别包含第1个周期及6个后续决策周期.

实验3(动态决策) 在不确定性环境下，基于随机场景信息，使用动态决策框架，即按照周期滚动求解两阶段近似优化模型，在各周期中采用两阶段禁忌搜索.

实验4(前摄-反应决策) 在不确定性环境下，基于无延迟的准点到港信息，采用实验2的方法生成初始计划，并采用右移(Right-shift)策略应对执行过程中的实际延迟.

实验2与实验1采用完全相同的信息进行后验优化，但其简化了所提动态决策框架下的两阶段禁忌搜索，各规模下的p1的均值均在4%以内，其z2值与实验1中Cplex软件的最优解或低界值很接近，从而验证了禁忌搜索算法的有效性，且其运算时间具有显著优势.

表1 数值实验结果Tab.1 Results of numerical experiments

实验3采用所提出的动态决策框架，在各规模下的p2的均值分别为4%、3%和2%，可见第2阶段决策中针对已知的随机场景信息做出可调整决策，可以有效应对不确定性因素的影响，获得更好的第1阶段固定决策，从而增强多阶段决策的后验优化.

实验4采用与实验3相同的不确定性环境，并用典型的前摄-反应决策方式.相比而言，动态决策框架所获在各规模下的p3的均值分别为7%、4%和4%，可见其充分利用了已知随机场景信息的必要性和有效性.

为了验证在更大规模下数值实验的效果，本文在V=50,60的条件下进行数值实验，所得结果见表2.其中，p4=(z3-z2)/z2.

由于Cplex软件在V=40时已经出现较多算例无法在可接受时间内求得精确解的问题，所以在更大规模下不进行实验1的求解.实验2是基于完全后验信息下采用所提出的简化两阶段禁忌搜索算法进行求解的，由表1可见其与实验1所求的解足够接近，因此，在更大规模下以实验2作为对比对象.

在V=60时，实验3在不确定环境下采用所提出的动态决策框架进行求解，所得结果与实验2的结果基本一致，其p4值均为0；而实验4与实验3的不确定环境相同，采用前摄-反应决策方式，相比而言，所提出的动态决策框架(实验3)在V=50，60下对z的改善程度(p3值)分别为7%和4%.

对更大规模的实验数据进行分析表明，所提出的基于随机场景的动态决策框架及两阶段禁忌搜索算法能够在各规模下有效地应对不确定性因素.

表2 大规模下的数值实验结果Tab.2 Results of large scale numerical experiments

4 结语

本文针对集装箱进出口码头泊位-堆场的调度问题，提出多阶段随机决策过程的两阶段近似、设计兼顾鲁棒性与灵活性的动态决策框架.一方面，通过判断并延迟B1类船舶的决策，充分发挥了准确信息的作用；另一方面，通过随机场景下的第2阶段可调整决策，充分利用了最新获得的不确定性信息.同时，通过数值实验中的不同策略对比，验证了所提方法的有效性.后续研究将考虑更复杂的不确定性环境，如装卸载箱量和天气等影响的因素.