交叉耦合带通滤波器的优化研究及仿真

王鹏博 严一尔

关键词： 滤波函数; 无载[Q]值; 拓扑结构; 交叉耦合; 滤波器优化; [Q]值补偿; 谐振器

中图分类号： TN713+.5?34                       文献标识码： A                         文章編号： 1004?373X（2019）03?0139?04

Abstract： The fifth generation of mobile communication technology has higher requirements for the filtering performance of the system， so the optimization of the filter is the key to ensure the performance of the system. On the basis of loss analysis of the filter function polynomial， the function relationship between the unload [Q]?value of the resonator and each filtering index is derived， and its simulation verification is carried out with the given topology structure. The compensation simulation is realized for unload [Q]?value of each resonator. The method of high [Q]?value resonator can improve the loss and response curves of the bandpass side frequency point. The goal of filter optimization design is realized.

Keywords： filtering function; unloaded [Q]?value; topological structure; cross coupling; filter optimization; [Q]?value compensation; resonator

0  引  言

在滤波器设计中小型化、高性能化成为通信滤波设备发展的新趋势，但随着谐振器腔体尺寸变小，其品质因数（Quality Factor）[Q]值也会进一步变小，由此带来了滤波器损耗变大，滤波性能恶化等问题。同时，滤波器的设计和综合都是在理想条件下进行的，忽略了在滤波器制作过程中各方面存在的损耗，因此实际做出的滤波器特性与初期设计时的特性存在着一定的偏差。以上两种因素严重影响了滤波器的特性，特别表现在插入损耗（Insertion Loss，IL）、反射损耗（Return Loss，RL）和矩形系数（Shape Factor，SF）的变化，主要体现在滤波特性曲线过于圆滑，出现“塌肩”的现象。

因此，在设计滤波网络初期，需要对各个无耗元件的传输响应函数进行修正，并对整体网络结构设计进行[Q]值补偿优化，从而减小损耗，使测试的特性曲线更加理想化，满足高性能滤波器件要求[1]。

1.2  零点拓扑研究

拓扑结构实质上反映了滤波器腔体、源S和负载L之间的组合状态，其中实线表示主耦合，虚线表示交叉耦合。文中对图1所示三种拓扑结构进行仿真分析，其中涉及CT和CQ两种实现零点的拓扑结构如图2所示。

交叉耦合结构可以产生零点，三腔耦合（Cascaded Triplet，CT）可以实现一个传输零点，四腔耦合（Cascaded Quadruplet，CQ）实现两个传输零点。

图2a）中分别为容性耦合和感性耦合结构，可以在低频端和高频端分别产生一个零点，其强弱均受控于②号腔，故②号腔称为零点腔[4]。相应地，在图2b）中零点腔为②和③。波形图中虚线为传输曲线（[S21]），实线为反射曲线（[S11]）。

2  仿真验证

对前文中推倒出的IL，RL，[SF]与变量[Qu]之间的函数关系进行仿真验证。

2.1  初始设计方案

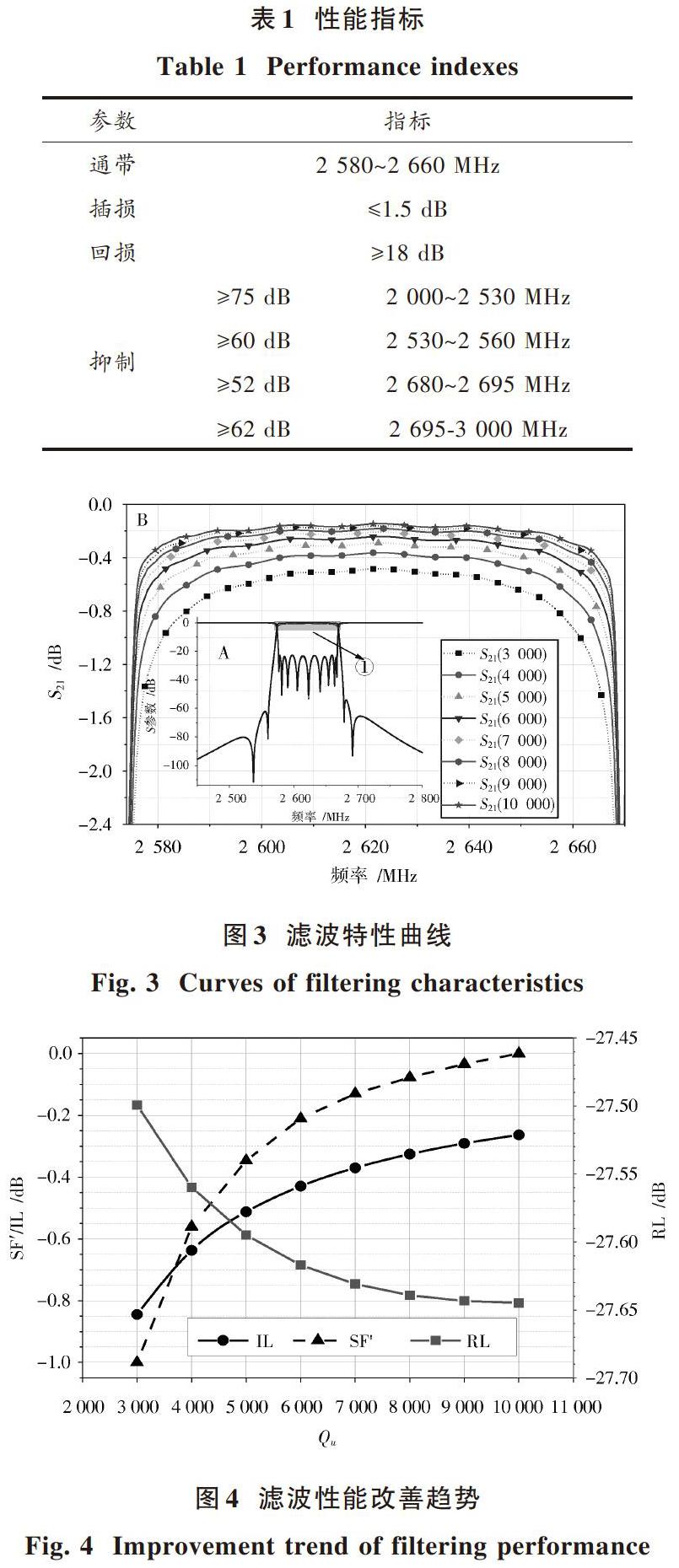
根据表1性能指标需求，通过CoupleFil初步评估，确定采用9腔4零点方案进行设计，初始[Qu]值为3 000，传输零点分别为：2 537.5 MHz，2 560 MHz，2 678.5 MHz，2 691.5 MHz。

2.2  [Q]值对性能的影响

图3中A为滤波器整体的仿真特性曲线，B为A中①处的区域放大图。从B中可以看出[Qu]值的等量增加有利于滤波性能趋于理想化的实现。

当初始[Qu]值在3 000～10 000的范围内以1 000为单位等量增加时，对IL，RL，[SF]指标影响如图4所示。图4展示了提高[Qu]对IL，RL，[SF′]的改善趋势。其中指标IL改善最为明显，接下来主要针对IL对全腔[Qu]值进行仿真，优化出需要补偿的[Q]值位置。

3  优化仿真

要设计性能最优的滤波器，先优化出对性能影响最大的一组极点，即判断出对IL影响最大的一组谐振器，通过补偿[Q]值的方法实现滤波器的优化设计[5]。为了降低仿真复杂度，故只对图1所示的拓扑结构进行代表性仿真，补偿[Q]值（[Qf]）统一拟定为10 000，并分别对高频端（High Frequency，HF）2 MHz、低频端（Low Frequency，LF）2 MHz及通带中心（Pass Band，PB）40 MHz的20个频点插损求平均值进行统计。

3.1  CT结构仿真

如图1a）所示，采用两感性两容性耦合的4CT拓扑结构，产生的零点波形如图2a）所示，其中②和④号腔为零点腔。图5和图6分别是对单个及两个谐振器进行[Q]值补偿仿真的结果，其横坐标是改善的谐振器编号，纵坐标为改善幅度。

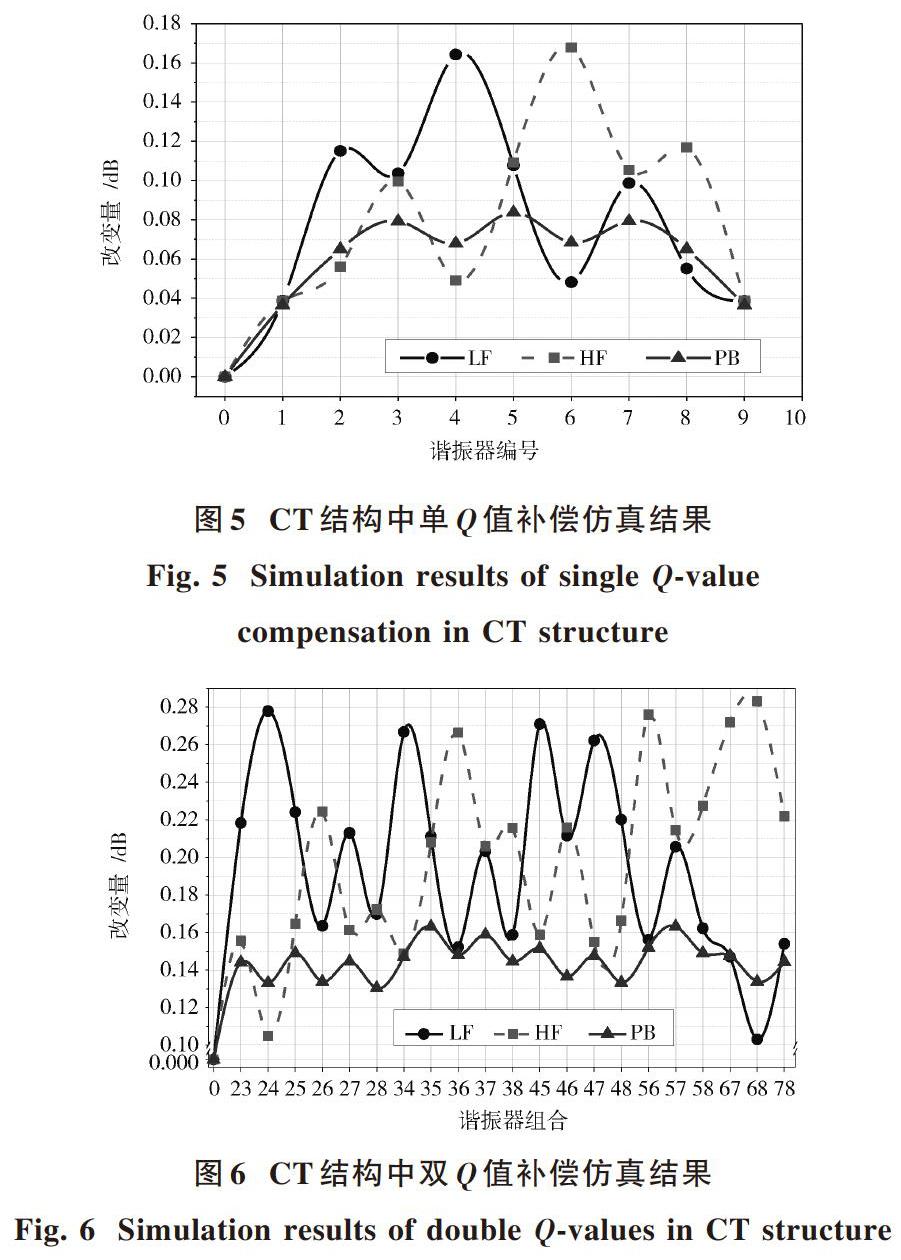
图5中对LF端影响较大的为④和②号腔，对HF端影响较大的为⑥和⑧号腔，对PB影响较大的为⑤、③和⑦号腔。而图6中省略对首尾腔的讨论，对LF影响较大的组合是②?④，对HF端影响最大的是⑥?⑧，对PB影响最大的是③?⑤和⑤?⑦组合。

从上述分析结果来看，双极点仿真结果可以看成是由单极点结果叠加而来，故接下来只针对单极点进行补偿仿真分析。

3.2  CQ結构仿真

如图1b）所示，采用2CQ拓扑结构，其零点波形如图2b）所示，相应单谐振器[Q]值补偿仿真结果如图7所示。

图7中对LF端影响较大的为②和③号腔，对HF端影响较大的为⑦和⑥号腔，对PB影响较大的为③和⑥号腔。

3.3  CT?CQ结构仿真

如图1c）所示，采用2CT?1CQ拓扑结构，其中①?③和③?⑤之间是容性耦合，⑥?⑧和⑥?⑨之间是感性耦合，相应零点腔为②④⑦⑧，相应单谐振器[Q]值补偿仿真变化如图8所示。

图8中对LF影响较大的是④和②号腔，对HF影响较大的是⑦和⑧号腔，对PB影响较大的是⑤和⑥号腔。

4  结  语

滤波器的优化设计标准就是达到带内低损耗，带外高抑制的滤波性能指标。图3，图4说明提高[Q]值可以改善滤波性能;图5～图8说明补偿零点腔的[Q]值对通带边频点的损耗改善效果最明显，且改善效果具有一定的叠加性，故零点腔越多，补偿后性能改善效果越好。

故在考虑成本的条件下，通过适当补偿零点腔谐振器的[Qu]值（传输TE模的介质谐振器具有很高无载[Q]值），以此来提升腔体的滤波性能，实现滤波器优化设计的目标[6?7]。

参考文献

[1] 罗杰，廖成.基于传输零点的广义切比雪夫型LC滤波器快速设计法[J].现代电子技术，2014，37（17）：129?131.

LUO Jie， LIAO Cheng. A rapid design method of generalized Chebyshev LC filter based on transmission zero [J]. Modern electronics technique， 2014， 37（17）： 129?131.

[2] 白冰.广义Chebyshev滤波器传输零点提取和优化[J].科技创新与应用，2014（18）：26?27.

BAI Bing. Transmission zero point extraction and optimization of generalized Chebyshev filter [J]. Technology innovation and application， 2014（18）： 26?27.

[3] 王雪.优化算法在微波腔体滤波器结构参数中的应用研究[D].北京：华北电力大学，2015：15?22.

WANG Xue. Study on optimization algorithm of microwave cavity filter structural parameters [D]. Beijing： North China Electric Power University， 2015： 15?22.

[4] SWANSON D， MACCHIARELLA G. Microwave filter design by synthesis and optimization [J]. IEEE microwave magazine， 2007， 8（2）： 52?69.

[5] 黄好强.大功率腔体滤波器优化设计[J].河北省科学院学报，2008（2）：36?38.

HUANG Haoqiang. The optimization design of high?power cavity filter [J]. Journal of the Hebei Academy of Sciences， 2008（2）： 36?38.

[6] 陈其豪，封建华，叶强.具有介质腔与金属腔体混合的新型带通滤波器的设计[J].中国计量学院学报，2015，26（3）：311?315.

CHEN Qihao， FENG Jianhua， YE Qiang. Design of a new type of band?pass of metal?dielectric resonant filters [J]. Journal of China Jiliang University， 2015， 26（3）： 311?315.

[7] 孙尚传.一种金属谐振器与介质谐振器组合应用设计高性能滤波器的方法[J].中国新通信，2013，15（1）：23?29.

SUN Shangchuan. A design method of high performance filter composite application of metal and dielectric resonator [J]. China new telecommunications， 2013， 15（1）： 23?29.

[8] 王皓陈，王志明.超高频带通滤波器的设计与仿真[J].现代电子技术，2013，36（14）：116?118.

WANG Haochen， WANG Zhiming. Design and simulation of ultra?high frequency bandpass filter [J]. Modern electronics technique， 2013， 36（14）： 116?118.

[9] ZHANG Qijun， GUPTA K C， DEVABHAKTUNI V K. Artificial neural networks for RF and microwave design： from theory to practice [J]. IEEE transactions on microwave theory and techniques， 2003， 5（4）： 1339?1350.

[10] 魏伟，许胜辉，孙剑波.一种无源滤波器的优化设计方法[J].电力自动化设备，2012，32（1）：62?66.

WEI Wei， XU Shenghui， SUN Jianbo. Optimal design of passive filter [J]. Electric power automation equipment， 2012， 32（1）： 62?66.