船用空压机装置故障诊断方法研究
2019-02-19尚前明胡浩帆
尚前明,胡浩帆,曹 召,王 潇
(武汉理工大学 能源与动力工程学院,湖北 武汉 430063)
随着对船舶安全性要求的提高,需要对船舶的一些关键机械加强故障后的及时诊断处理。空压机作为一种为船舶主机启动提供动力的机器,其重要性不言而喻。在船舶运行中,由于空压机工作环境恶劣、设备维护成本高以及失效模式多样[1],所以一旦空压机不能正常工作,会对船舶造成很大伤害,轻则危害船舶安全运行,重则危害船员生命。根据以往统计,上世纪80年代,我国发生空压机事故200多起,造成了不可估计的经济损失。
本文通过对船舶已往事故的分析,建立了空压机常见故障的故障树,并完成了向贝叶斯网络的转化。当船舶发生故障时可以通过贝叶斯网络分析查找最可能发生故障的原因,为船舶工作人员提供科学、可靠的指导依据,缩短维修时间,尽可能减轻故障带来的后果。
1 故障树理论和贝叶斯网络理论
1.1 故障树理论
故障树是通过树状图形来直观的表达设备可能发生故障的原因,并表明这种故障原因之间的关系。故障树分析法是把最不期望出现的故障模式设置为顶事件,通过专家意见和往期故障找出故障发生的全部因素,然后找出引发这些因素的全部原因作为下一级,直到故障原因无法再分,结束建树过程[2]。故障树分析的流程如图1。
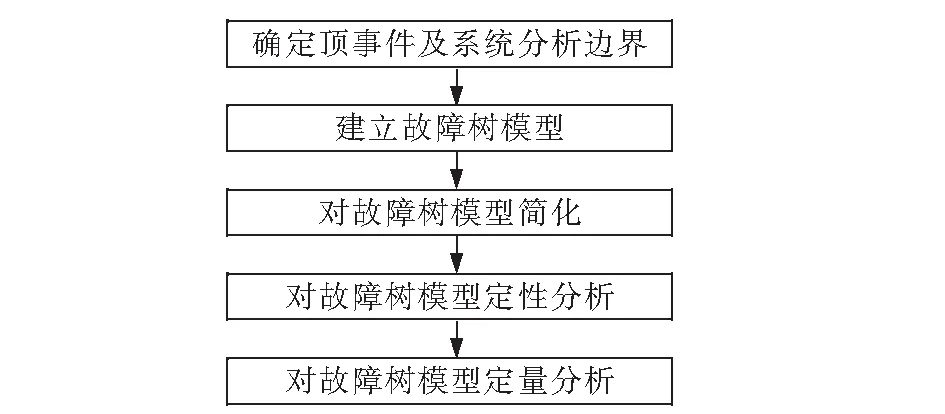
图1 故障树分析流程图
定性分析:通常是在建树之后,对故障树采用最小割集和最小径集进行分析,得到各种故障事件的概率,并根据概率大小确定设备的安全保护措施。
定量分析:所谓定量分析就是在一定假设条件下得到底事件的结构重要度等量化指标。结构重要度公式如式(1)所示。
(1)
式中:Iφ(i)为基本事件i的结构重要度系数;n为基本事件数量;φ(1i,x)表示系统发生故障;φ(0i,x)表示系统正常工作。
1.2 贝叶斯网络
贝叶斯网络[3]是用图形化的方式表示各个事件的关系及概率分布,它是一种有向无环图。图2为一种简单的贝叶斯网络模型实例。

图2 贝叶斯模型实例
一般贝叶斯用B(G,P)符号表示,其中G为有向无环图,P为条件概率表。
1)先验概率。设X1,X2,...,Xn为样本集合T中的事件,则Xi发生的概率即为先验概率P(Xi)。先验概率可以通过以往的数据计算得出,在新机刚投入运行时或缺少数据时也可以根据专家经验进行打分表决。本文即通过专家打分得出先验概率。
2)条件概率。它是在已知某一事件的情况下另一事件发生的概率。如A、B为不同的事件,且P(B)≠0,则称概率P(A/B)为A发生的情况下B发生的概率。其表达式如下所示。
(2)
3)后验概率。它是指根据已知事件发生的情况对先验概率进行改善得到更准确的概率,是贝叶斯网络的完善,也是故障诊断中由结果推断出原因的关键一步。
2 空压机故障树分析
2.1 故障树模型建立
空压机的典型故障主要体现在“排气量不足”“滑油变质”“不正常噪声”“排气温度过高”4个方面,下面以“排气量不足”分析故障(其它故障分析流程类似),空压机排气量不足故障树如图3所示。

图3 “空压机排气量不足”故障树模型
2.2 模型分析
1)定性分析。求最小割集和最小径集:按照行列式法求出故障树的最小割集有128个。把图3的“与”逻辑门和“或”逻辑门相互对换,把故障事件转为成功事件,然后求所得故障树的最小割集,求得的最小割集就是原先故障树的最小径集。求得的最小径集为:
P1=(D1,D2),
P2=(D3,D4,D5,D6,D7,D8,D9,D18),
P3=(D10,D11,D12,D13,D14,D15,D16,D17)。
2)定量分析。排气量不足底事件的结构重要度由式(1)可以计算得出,结果如表1所示。

表1 底事件的结构重要度
根据对故障树的定性分析、结构重要度的计算,我们可以化简故障树,即除去故障树中的重复冗余和一些重要度比较小的事件。如图4为化简后的船用空压机排气量不足故障树简化模型。
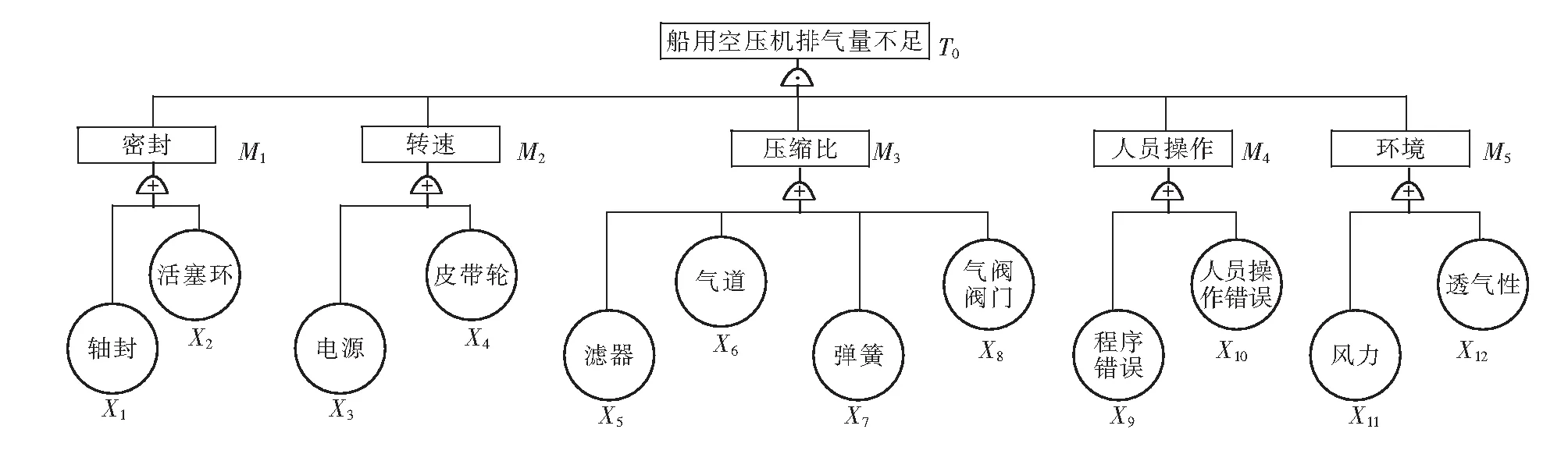
图4 “空压机排气量不足”简化故障树
3 空压机贝叶斯模型建立与分析
3.1 贝叶斯网络模型的建立
FN和FTA在结构上存在一定的映射关系,由FTA可以方便的构造出FN。FTA转FN的对应关系如图5所示。按照以上规则转化后的贝叶斯网络模型如图6所示。

图5 故障树到贝叶斯网络的映射关系图

图6 “空压机排气量不足”贝叶斯网络模型
3.2 贝叶斯网络概率的模糊计算
现在事件发生的状态一般都是连续性的,存在一定的模糊性,获得精确概率也是比较难的。基于以上原因我们可以根据现代专家多年积累的经验,运用模糊理论的方法得到不同状态的精准值[4]。
1)模糊概率的处理。模糊数在处理不确定性问题上被广泛应用,目前最常用的模糊数为三角模糊数和梯形模糊数。三角模糊数较梯形模糊数在解决问题时运算比较简单,函数分析也较容易。因此我们选用三角模糊数进行概率的确定。
三角函数的隶属度函数为:
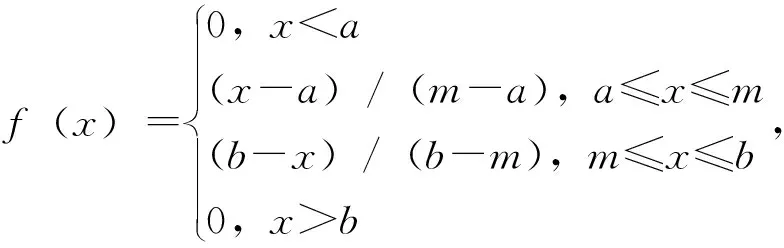
(3)
由隶属度函数可以看出三角数可以由(a,m,b)表示。为了方便专家打分我们规定了以下7种语义值来分别代表不同的模糊数,如表2所示。其对应的三角模糊数的隶属度函数如图7所示。

表2 事件发生概率语义值及相应的三角模糊数
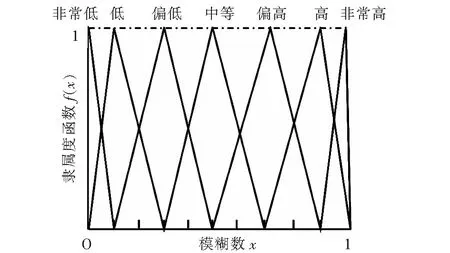
图7 三角模糊数的隶属度函数
为了更加准确地利用模糊数来刻画事件发生的可能性,有必要对多位专家的语义评判进行合成。本文采用加权求和的模糊数合成方式,令Wj表示第j位专家的权重值 (j=1,2,…,n),Fji表示第j位专家对第i个事件的语义评判模糊数 (i=1,2,…,m),则事件i的综合评判Mi可如下式表示:
Mi=W1F1i+W2F2i+…+WnFni,
(4)
2)解模糊。为了得到精确概率,需要对模糊概率进行处理,本文采用均值面积法进行解模糊处理,其公式如下。
(5)

3)概率归一化。贝叶斯网络的基本事件各个状态概率之和必须为1,因此我们要对以上得到的精确概率进行概率归一化处理。
(6)
其中,各根节点的先验概率根据历史故障数据分析以及相关专家意见。邀请4位领域内的知名专家对空压机故障基本事件的先验概率给出评价意见。专家的基本信息和权重如表3所示。
按1)~3)所示分析步骤对模糊数进行处理得到先验概率,其分析结果如表4所示。

表3 专家权重表
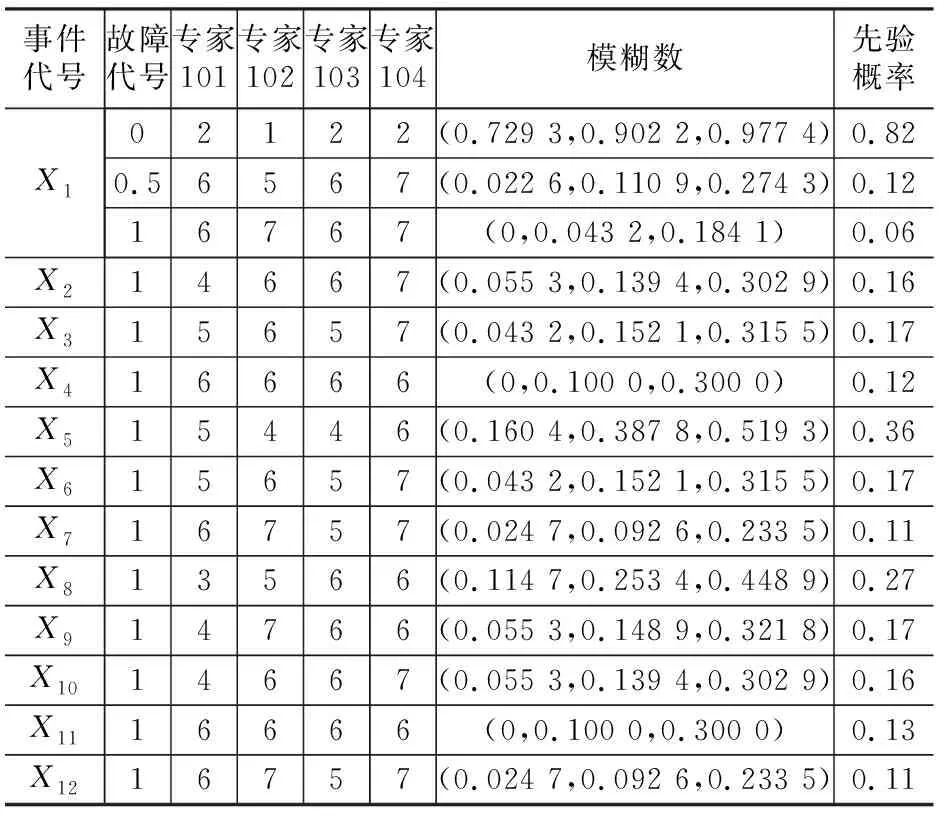
表4 各根节点的先验概率
3.3 贝叶斯网络模型的建立与验证
贝叶斯网络的先验概率确定下来后,我们需要求得其条件概率,和上述方法一样由领域专家打分计算出的条件概率表(CPT)如表5所示。其中正常表示空压机处于正常运转状态,故障表示空压机处于事故状态。
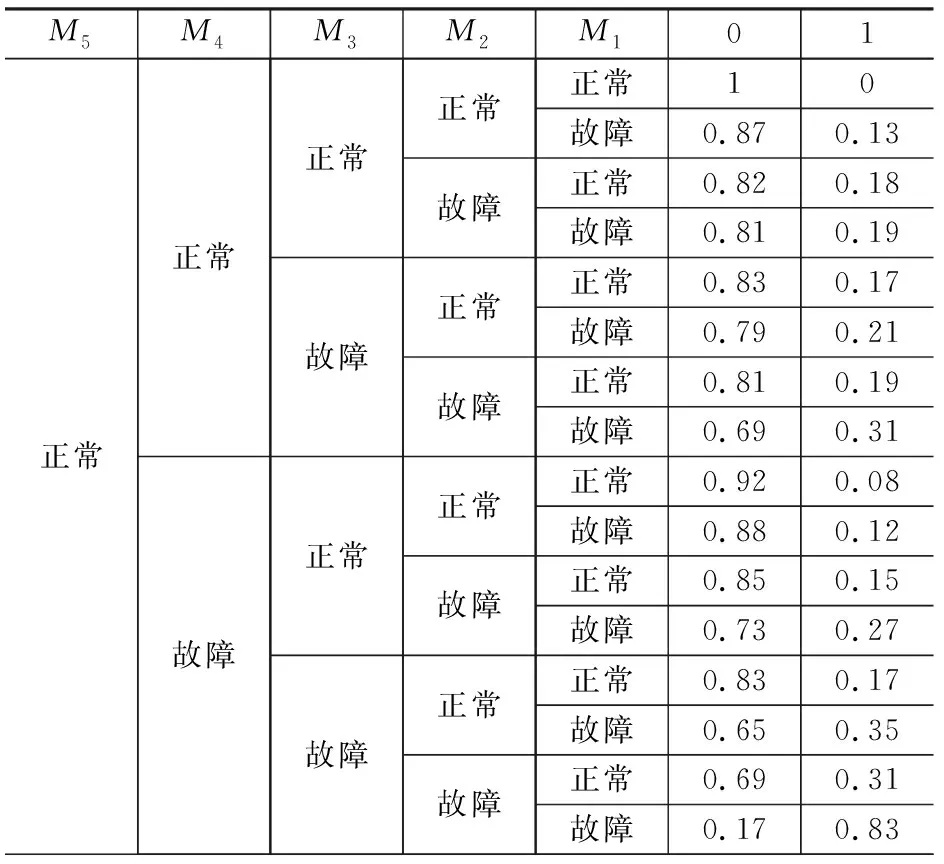
表5 空压机的CPT
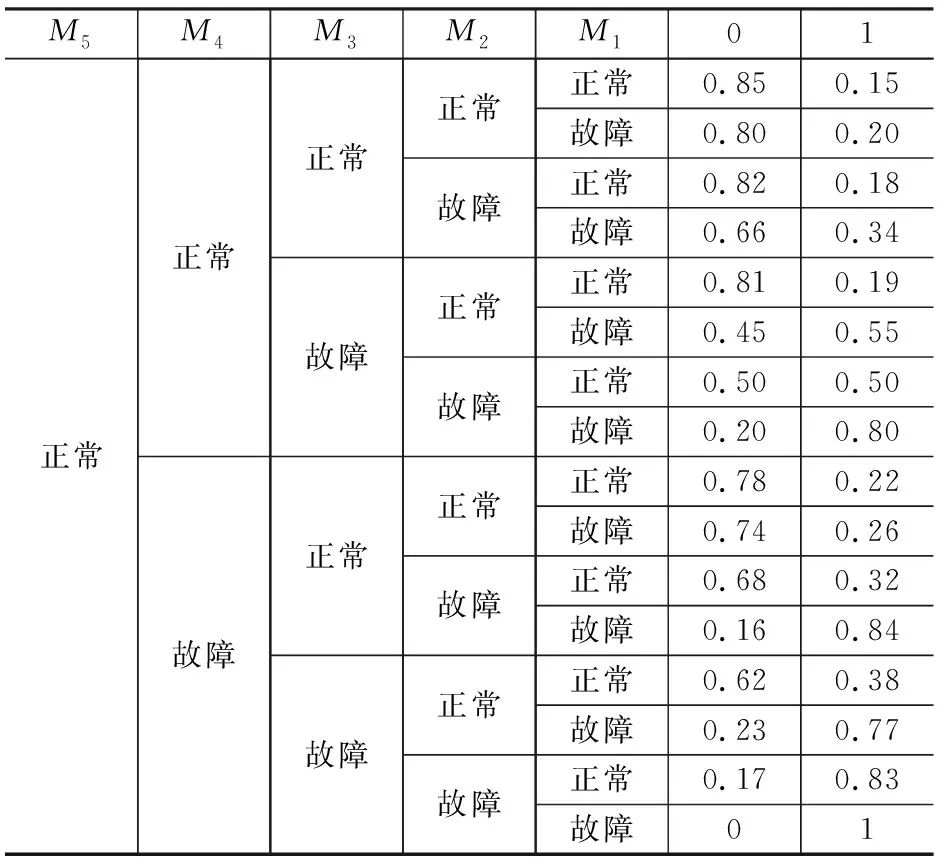
续表5 空压机的CPT
确定节点条件概率分布。至此空压机排气量不足模型已经建好,下面以28 000 t散货船为例分析。2012年7月该船空气瓶压力为1.5 MPa,出现低压报警。此时空压机转速>110%,排气压力为0.42 MPa,风力为4级,透气性良好,压缩比为5。
将信息输入“透平机停机”贝叶斯网络模型,得到结果如图8所示。
由分析可知最易发生故障的是滤器。由当时处理结果可知滤器中杂物较多,与上述分析结果相符。轴承磨损,与运算结果相符合,证明模型具有一定的可靠性。

图8 “空压机排气量不足”贝叶斯网络模型运算结果
