海上风电场微观选址及输电线路规划研究

2019-02-18李岩吴迪刘怀西葛文澎曾冠毓

风能 2019年10期

李岩吴迪刘怀西葛文澎曾冠毓

目前海上风电已成为风电行业发展的主趋势。随着全球海上风电市场迅速扩张。如何提高风电场全生命周期收益、降低建造及运维成本，成为业内主要关注的议题之一。

当前国内外部分学者对海上风电场如何合理微观选址及规划输电线路进行了相关研究。有学者为优化海上风电机组排布方案提出了多目标进化算法与嵌套式遗传算法，但该优化算法得出的风电机组排布方案不规则，直观感差且不利于前期的建设与后期的运维工作。针对海上风电场输电线路优化，有学者提出了动态最小生成树算法和混合整数线性规划模型，两种方法可实现对大型海上风电场输电线路的自动规划，但其没有详细考虑不同规格电缆的负载能力、避让限制区等因素。因此有必要对海上风电场的机组排布及电缆布置进行更精细的优化研究。

本文以海上风电场为研究对象，提出一种适用于任意封闭边界形式的风电场机位优化方法。该方法能有效降低风电场尾流损失，大幅度提高发电量。此外，为得到低成本的电缆布置方案，改进了Esau-Williams智能算法。得到一种风电场线路快速规划方法，可同时规划不同规格电缆，且一次规划能得出多种较优方案。风电场模型

一、尾流模型

风沿某一方向流经风电场时，上游风电机组在捕获风能的过程中，会在风电机组后方产生风速下降的尾流亏损区，使得下游风电机组发电量因迎流风速减小而降低，这种现象称为尾流效应。Jensen尾流模型是目前行业内应用最广泛的一种尾流模型，该模型由Jensen等学者于上世纪八十年代提出。其假设风电机组后方的尾流亏损区是轴对称形式的，且风速随距离增加呈线性恢复。模型示意图如图1所示，图1（a）中T1与T2分别代表上游风电机组与下游风电机组，u代表来流风速，u_loss代表风速亏损值。

风电机组尾流区扩张程度由尾流衰减因子k来表征，当下游风电机组处于上游风电机组尾流区时，下游风电机组处的风速亏损系数C_def按公式（1）计算，k值常按经验公式（2）计算。

式中，Ct为风电机组推力系数;D为风电机组风轮直径，m;A_ol为下游风电机组叶轮面与上游风电机组尾流截面重叠区面积，m²;A_t2为下游风电机组叶轮扫风面积，m²;H为风电机组轮毂高度，m;z为地表粗糙高度，mo

对于海上风电场而言，海面粗糙高度常取0.0002m。某一风向下，当一台风电机组同时受多台风电机组尾流影响时，尾流亏损的累计效应通常应用公式（3）计算。

式中，C_def，i为第i台风电机组风速总亏损系数;C_def，i，j为第j台风电机组对第i台风电机组造成的风速亏损系数。

二、发电量计算

计算风电场发电量时，首先常用威布尔函数对风电场内风速数据进行描述。公式（4）为威布尔分布函数，该函数可计算出任一风速“发生的概率p（u）。

式中，A为威布尔尺度参数，m/s;K为威布尔形状参数;u为来流风速，m/s。

风电场年发电量P_AEP的计算，需要获得风电机组的功率特性、风电机组排布和风能资源等信息，公式（5）为P_AEP的计算式。目前常用的风能资源数据统计方法为将测风数据转化为风速风向分布矩阵，在每一风向下风速子区间内分别计算发电量，然后按加权求和的方式得出總发电量。风电机组尾流损失值δW为风电机组由于尾流亏损造成的发电量损失与理论发电量之比，公式（6）为其计算式。

式中，T为一年发电小时数，T=8760h;Nd为均匀划分的风向扇区总数;N_Wt为风电机组台数;p_s，i为第i风向扇区下的风频;u_ci，j为第j台风电机组的切入风速，m/s;u_co，j为第j台风电机组的切出风速，m/s;Pt，j（u）为第，台风电机组在风速u下的输出功率，MW;pi，j（u）为第j台风电机组在第i风向扇区下的风频;pt为风电场理论年发电量（不考虑风电机组尾流效应）。MWh。

三、尾流模型准确性验证

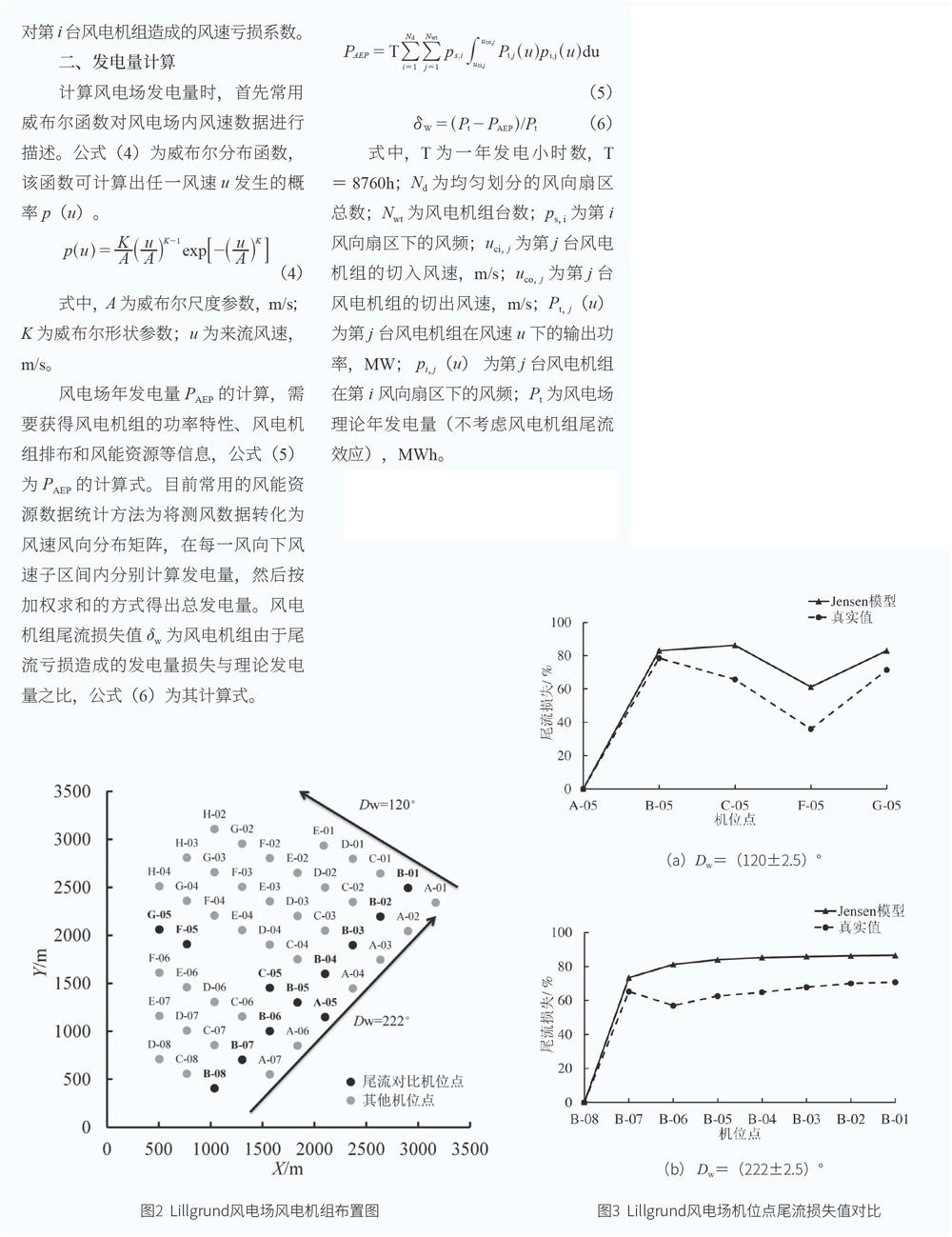
为验证Jensen模型的准确性，以Lillgrund海上风电场为研究对象，Lillgrund风电场位于厄勒海峡，距离瑞典西海岸约7 km，由48台西门子SWT-2.3-93型风电机组组成，风电机组额定功率为2.3 MW。轮毂高度为65m，风轮直径为92.6m。风电场机位布置图如图2所示，图中Dw代表来流风向，图中黑色和灰色点均为风电场机位点，其中黑色机位点为尾流损失对比机位点。

在此对比来流风速在（9±0.5）m/s区间范围，风向分别在（120±2.5）。和（222±2.5）°区间范围时，部分风电机组的尾流损失情况。其中机位尾流损失的真实值来源于文献中记录的风电场实际监测数据，图3为Lillgrund风电场部分机位点基于Jensen模型计算的尾流损失值与真实值的对比。

图3显示Jensen模型计算的风电机组尾流损失值与真实值较吻合，同时计算值整体高于实际值，当风向区间为（120±2.5）°时，尾流损失计算值平均比实际值高12.4%：当风向区间为（222±2.5）°时，尾流损失计算值平均比实际值高14.5%。经分析差异主要来源于Jensen模型假设风电场中各机位点处风向、风速均一致，而实际风电场中无法满足该假设，因此不可避免会引入一定误差。从风电场机位尾流损失的快速预测方面考虑。Jensen模型计算值与真实值误差在可接受范围内，即Jensen模型在风电场风电机组尾流损失预测中具有一定的适用性与准确性。

机位优化策略

本文算例中风电场尾流模型选用Jensen模型，利用Python语言对该模型进行程序实现，输入机位点位置、风电机组参数、风能资源等信息，便可快速求解出各机位点的发电量及尾流损失值。

一、网格型排布优化

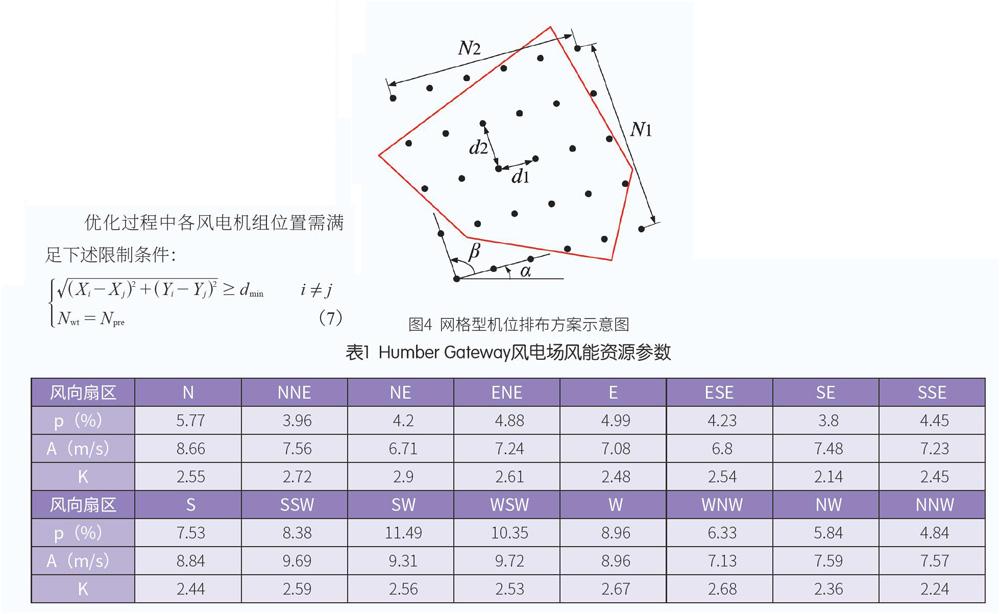
网格型机位排布以其美观、通航性好等优势，在海上风电行业得到了较高的认可。如图4所示，风电场网格型机位排布中最小布置单元为平行四边形。该类型风电场机位排布由以下参数定义：风电场内风电机组排数N1与列数N2，列间距d1，排间距d2，每一排风电机组与水平轴的夹角a（水平轴指向正东方向），风电机组排与列的夹角β。

风电机组排布方案的制定需明确风电场的场址边界（如图4中红色多边形）和风电机组预安装总台数Npreo本文借助Python语言实现了风电机组的网格型排布优化，优化过程对d1、d2、a和β等参数进行遍历取值，并以风电场发电量最大为优化目标，尾流模型选用Jensen模型。经验证利用高性能计算机，可在数小时内完成近百台风电机组规模风电场的网格型排布优化过程。

优化过程中各风电机组位置需满足下述限制条件：

该限制条件分别代表各风电机组间距均不小于极限机距dmin、风电场边界内风电机组台数与预安装台数相同。在优化过程中方案参数d1和d2均以dmin。为取值下限，取值上限视风电场占海面积决定;a角的取值范围为[0°，180°）;当β角接近0°或180°时，风电场内风电机组的排与列布置大致趋近于同一直线，这与实际经验不符，因此β角的取值范围一般为[20°，160°]。

二、机位优化算例

以Humber Gateway海上风电场作为优化对象，此风电场位于英格兰北侧海域，离岸距离约10 km，由73台维斯塔斯公司V112-3.0MW型风电机组组成，总装机容量为219MW，风电场占海面积约为28 km²。在此参考该风电场海拔100 m处Merra2中尺度风能资源数据，各风向扇区下的风频和风速威布尔参数见表1，考虑到海上风电机组逐渐走向大容量化，在此以某5.5MW海上风电机组为推荐机型，该机型额定功率Pe为5.5MW，风电机组风轮直径D为158 m，轮毂高度H选取100 m，风电机组的切入和切出风速分别为3 m/s和30m/s，结合本风电场总容量推荐风电机组台数为40台。

为研究风电机组间最小距离对风电场发电量的影响，对上述风电场进行机位排布优化时设置dmin分别为3.0D、3.5D和4.0D，优化得出的最优方案布置图见图5，表2汇总了不同极限机距最优方案的发电量等信息。

由表2数据可知，本算例中风电机组极限机距dmin。为3.0D方案的发电量最大，然后依次是dmin为3.5D的方案和dmin为4.0D的方案，结果表明本算例在一定范围内极限机距越小，网格型排布方案发电量越高，但风电机组间距过小不利于风电机组的安装及维护，行业内通常建议风电机组间距不小于3.0D。此外，三组排布方案的参数a角均处于118°附近，同时西南和西南偏西风向为本风电场的主导风向，即最优网格型排布方案中各排风电机组的连线均与主风向大致垂直。输电线路规划

Esau-Williams智能算法起初是为了解决远程通信系统布局问题而提出的，待解决问题中存在一个处理中心与多个终端点，规划目标是将各个终端点与处理中心实现直接或间接连接。且电缆成本最低。

由于可行的连接方案数随着终端点数增加而呈指数级上升，凭现有计算能力无法全部使用遍历方法。基于此，Esau-Williams算法采用了一种逐步寻优策略：

（1）首先将每个终端点都与处理中心直线连接作为初始方案，该方案通常为成本最昂贵方案，如图6（a）所示。

（2）随后尝试将不同终端对进行连接，即减少直接连接到处理中心的线缆条数。建立不同终端之间的距离矩阵和可行任务栈。对终端逐对连接，计算连接后方案的线缆成本，若成本降低，则把该方案存入可行任务栈中。

（3）终端逐对连接计算后，选取可行任务栈中成本降低最多的终端对进行正式连接，更新中间方案，如图6（b）所示。若该步骤计算得出连接终端A、B后，节省的成本最多，则在A与B之间增设电缆，并将B到中心的线缆淘汰。

（4）方案更新后，重复（2）、（3）步骤，直至可行任务栈中无连接方案，如图6（c）、6（d）所示，即优化过程结束，输出最终方案。

一、Esau-Williams算法改进

以上寻优过程中，需保证电缆之间无交叉，经验证对于数百规模终端数的优化过程该算法仅需数秒时间，但算法没有考虑单个回路上终端数的数量限制，无法直接应用到海上风电场电缆规划中。为解决海上风电场电缆规划问题，需对原始的Esau-Williams算法进行改进，改进过程中将电缆负载因素类比引入，通过判断各回路上不同子线路的负载能力，使其可进行不同规格电缆的同步优化，同时保证每条接回升压站的电缆上所连接的风电机组数不超过限制值。此外，原算法每次优化仅能得出一组同一方案，无法进行不同方案的评估，且不能限制风电机组输电线缆的回路数。为解决该类问题，本文尝试在每步优化过程中随机选取可行任务栈中的连接方案，设置选取的概率与节约成本成正比，而非每次均选择最节约的连接形式。通过不断重复优化，可得出多种不同的优化方案，继而可在得到的可行方案库中选取最终方案。

二、输电线路规划算例

以上文HumberGateway风电场优化方案二为输电线路规划算例，风电场海上升压站位于场区西北侧。结合风电场容量及风电机组功率，推荐使用额定电压35 kV，横截面积分别为（3×70）mm²、（3×150）mm²、（3×300）mm²和（3X400）mm²的海底绝缘电缆，四种电缆成本分别为（81.6、113.4、173.0、190.0）万元/千米。经载流量计算。（3×70）mm²截面电缆可连接1～2台5.5MW风电机组，（3×150）mm²电缆最多可连接3台5.5MW风电机组，（3×300）mm²电缆最多可连接4台5.5MW风电机组，（3×400）mm²电缆最多可连接5台5.5MW风电机组。对本风电场进行输电线路自动规划，结果显示得出的方案中连接到海上升压站的电缆回路为9至11回。在此分别选取三种不同回路数的最低成本方案，具体方案见图7，图中（3×70）mm²、（3×150）mm²、（3×300）mm²和（3 X400）mm²电缆分别用蓝线、红线、绿线和黑线表示，表3记录了三种方案的电缆用量及成本。