基于支座动位移监测的高铁桥梁支座磨损状态安全评估
2019-02-18王高新丁幼亮
王高新,丁幼亮,刘 华,岳 青
(1.中国矿业大学 力学与土木工程学院,江苏 徐州 221116;2.东南大学 土木工程学院,江苏 南京 210096;3.中铁大桥(南京)桥隧诊治有限公司,江苏 南京 210032)
我国自2008年高速铁路投入运营开始,国内高速铁路网飞速发展。随着高速铁路桥梁服役时间的增长,一些关键性桥梁构件在外界环境和各类荷载作用下产生老化和损伤。支座作为大跨铁路桥梁结构的重要受力构件之一,在实际运营中会出现支座变形磨损和承载力下降等问题,会直接影响到铁路桥梁的安全运营。在实际服役环境下,支座位移时程包含由列车荷载引起的动位移成分,这些动位移成分通过不断累积,可造成支座内部聚四氟乙烯板磨损严重,进而危害到支座使用寿命,因此,有必要进行高速列车荷载对桥梁支座磨损状态影响研究。
目前研究很少关注列车荷载作用下大跨铁路桥梁支座的累积疲劳损伤问题。已有研究主要侧重于温度场作用下大跨铁路桥梁支座的服役状态,例如Yan Bin等人针对上海—昆明沿线1座连续梁桥支座的摩擦阻力进行了分析[1],结果表明温度作用下支座的摩擦阻力会对车桥耦合系统的力学特性产生影响。高速铁路大跨度桥梁具有设计车速高和行车轨道多的特点,例如大胜关长江大桥的主跨为336 m,其设计车速达到300 km·h-1,行车轨道共有6条线。然而目前的研究尚未明确高速列车荷载作用下支座累积行程的变化规律,也未给出支座磨损状态的安全评价方法。
本文以南京大胜关长江大桥为研究对象,基于其球形钢支座的纵向动位移监测数据,开展各次列车过桥时支座动位移累积值的概率统计分析,研究多次列车持续加载对支座累积行程的影响,在此基础上计算球型钢支座在设计使用寿命内的累积行程达到磨损上限的失效概率,基于该失效概率对球形钢支座在实际服役环境中的磨损状况进行安全评价。
1 桥梁概况
南京大胜关长江大桥,位于既有南京长江大桥上游约20 km的大胜关河段,是沪汉蓉铁路和京沪高速铁路共用的跨江通道,同时搭载双线地铁,具有体量大、荷载大、跨度大、速度高“三大一高”的显著特点,是世界首座6线铁路大桥。其主跨336 m的设计尺寸名列世界同类高速铁路桥梁之首。大桥设计速度为300 km·h-1,处于世界先进水平。
大胜关长江大桥的主桥结构是6跨(108+192+336+336+192+108)m的大跨度桥梁,如图1所示,由3片主桁拱、桁间支撑、钢桥面板以及横向加劲梁等组成。其中主桁拱包括箱型截面上弦杆、箱型截面下弦杆、箱型截面桥面弦杆、工字型斜腹杆以及竖腹杆等组成,桁间支撑又由水平支撑和竖向支撑组成。

图1 南京大胜关长江大桥
南京大胜关长江大桥沿纵桥向共布置7组大型球型钢支座,每组球型钢支座沿横桥向又包含1个上游支座、1个中间支座和1个下游支座。其中,中间桥墩处的球型钢支座为固定支座,其余球型钢支座允许主梁沿纵桥向进行自由伸缩。
2 传感器布置及动位移监测
2.1 传感器布置
由于中间桥墩处的球型钢支座为固定支座,因此在其余6个桥墩上游测和下游侧共12个球型钢支座D1,u~D3,u,D5,u~D7,u,D1,d~D3,d和D5,d~D7,d处安装12个水平位移计(u代表上游侧,d代表下游侧),如图2所示,对各球型钢支座处的纵向水平伸缩位移进行监测和数据采集。采样频率设定为1 Hz,采样时间是从2013年3月1日至2013年10月31日。已有研究表明[2],南京大胜关长江大桥的结构形式具有对称性特点,各个支座处的纵向位移值是以4号桥墩处的固定支座为对称中心,向两侧呈对称分布,因此本文仅选取左半对称结构中的球型钢支座D1,u~D3,u和D1,d~D3,d的纵向位移值进行分析。

图2 南京大胜关大桥上的位移传感器布置(单位:m)
2.2 动位移监测结果
2.2.1 时变位移
在桥梁上游侧,第i(i=1,2,3)个球形钢支座Di,u处的纵向位移监测值记为Di,u;在桥梁下游侧,第i个球形钢支座Di,d处的纵向位移监测值记为Di,d。由于各个支座纵向位移的时程曲线具有相似的变化趋势,因此以支座纵向位移监测值D1,u作为典型案例开展分析。图3给出了支座D1,u的纵向位移监测值D1,u的时程曲线。由如图3(a)可以看出,支座纵向位移监测值在2013年3月至2013年10月的8个月内的时程曲线具有典型的季节变化特征,即纵向位移值的整体变化趋势自3月至8月逐渐升高,又从8月至10月底逐渐回落。由图3(b)可以看出,支座纵向位移监测值在1 d内的时程曲线具有典型的正弦函数变化特征。需要指出的是,支座纵向位移的季节变化特征和正弦函数变化特征与温度场的变化特征很相似[3],据此可推知支座纵向位移主要是由结构温度场引起的。此外,由图3(c)D1,u在2013年4月18日8:00至9:00内的时变曲线可以看出,支座纵向位移包含着许多随机波动的动位移,这主要是由列车荷载引起的。

图3 支座D1,u纵向位移监测值D1,u 的时程曲线
可见,支座纵向位移同时包含由结构温度场引起的纵向静位移和由列车荷载引起的动位移。
2.2.2 累积位移
为研究列车荷载作用对支座磨损状态的影响,首先需要从支座位移监测数据中提取出动位移。纵向静位移与动位移存在明显区别,即静位移相对动位移而言变化较为缓慢,也就是两者处在不同的频带范围内。已有研究表明,动位移的主要频率在[5/86 400,0.5] Hz范围内[4-5]。由于小波包分解法能够根据信号特性和分析要求自适应地选择相应频带与信号频谱匹配,分解出信号的低频部分和高频部分,提高时频分辨率,为信号提供更为精细的分析方法,因此本文利用小波包分解法将处于频带[5/86 400,0.5] Hz范围内的动位移提取出来[6-9]。
利用小波包分解法,对支座位移监测数据进行小波包分解,得到具有不同频率特征的小波包系数,筛选出处于频带[5/86 400,0.5] Hz内的小波包系数并进行信号重构,得到每次高速列车引起的动位移时程。每次高速列车过桥便产生1个动位移时程,将每个动位移时程换算为动位移累积值(即计算单次列车荷载引起的支座累积行程),以此反映各次高速列车作用对支座累积磨损的影响。单次列车通过后,不同支座具有不同的累积值,其中支座Di,u具有的累积值记为Ni,u,支座Di,d具有的累积值记为Ni,d。自2013年的8月10日至2013年的8月31日这段时间内,根据行车监测系统的统计结果,共有3 495次高速列车通过此桥。计算在此时间段内各个球型钢支座的3 495个动位移累积值,计算结果如图4所示。由图4可以看出,各个球型钢支座的动位移累积值均具有一定的均匀随机分布特性,因此可推断动位移累积值具有一定的概率统计特性。进一步取平均值分析,即将各个球型钢支座的3 495个累积值取平均值,结果对应标注在图4中。可以看出:位于支座D3,d处的平均值最大,为7.020 mm,即在平均意义上列车荷载对支座D3,d的累积磨损影响最大;位于支座D1,u处的平均值最小,为2.904 mm,即在平均意义上列车荷载对支座D1,u的累积磨损影响最小。

图4 各支座动位移累积值的计算结果
3 支座磨损状态安全评估
3.1 蒙特卡洛抽样模拟
支座磨损状态安全评估要求大样本数据,而较短采集时间段内的支座位移监测数据通常难以满足这一要求,因此进行蒙特卡洛抽样模拟。考虑到支座累积行程是将动位移累积值不断累加得到的,因此将对支座累积行程的抽样模拟等效为对动位移累积值的抽样模拟并累加得到,而对累积值进行抽样模拟的第1步便是明确累积值的概率统计特性。
由于统计变量Ni,u和Ni,d的累加分布函数未知,在此选用3种累加分布函数,即Normal分布(正态分布)、Weibull分布(威布尔分布)和GEV分布(广义极值分布),利用Matlab软件中的累加分布函数拟合工具箱确定这3种累加分布函数的具体参数估计值,通过拟合效果对比确定最接近实测累加概率统计特性的分布函数。
以统计变量N1,u为例进行分析。对3种累加分布函数进行参数拟合,得到N1,u的3种累加分布函数如图5所示。
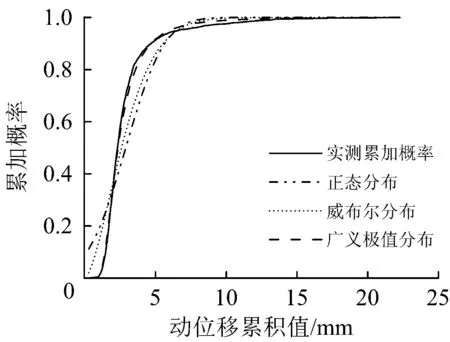
图5 N1,u的3种累加分布函数对比
通过对比可见,GEV分布与实测累加概率的吻合效果最好,因此选用GEV分布作为统计变量N1,u的累加分布函数,其公式为
(1)
式中:G(N1,u)为统计变量N1,u的GEV分布;r,a和b分别为GEV分布的形状参数、比例参数和位置参数。
利用Matlab软件中的累加分布函数拟合工具箱,确定GEV分布的参数估计值为:r=0.305 8,a=0.816 3和b=2.029 4。
基于上述分析方法,得到的各统计变量N1,u~N3,u和N1,d~N3,d的累加概率拟合曲线及其参数估计值如图6所示。由图6可以看出,各拟合曲线均与实测累加概率的吻合效果较好,表明采用GEV分布可以较好地描述累积值的累加概率特性。

图6 各支座累积值的GEV分布结果
已知支座累积值的概率统计特性服从特定的GEV分布,因此利用GEV分布对累积值进行蒙特卡洛抽样模拟,从而得到期望个数的动位移累积模拟值,在此基础上进一步将所有的累积模拟值累加,便可得到由多次列车荷载引起的支座累积行程模拟值。具体而言,若要通过模拟得到m个累积值,需要首先在(0,1)范围内的累积概率值中进行m次均匀随机抽样,得到数值在0~1之间的m个抽样值,然后将每个抽样值带入式(1),得到m个累积模拟值Ni,us或Ni,ds。
在对支座累积行程进行抽样模拟之前,首先计算支座累积行程的实测结果,以便与模拟结果进行对比。将图4中自2013年的8月10日至2013年的8月31日这一段时间内的3 495个累积值进行累加,便可得到在3 495次高速列车作用下各个支座的累积行程如图7所示,图中Mi,u为Di,u的累积行程,Mi,d为Di,d的累积行程。由图7可以看出:各支座累积行程均随列车次数增加而线性增长,且各累积行程的线性增长速率之间存在一定差异,其中M3,d的线性增长速率最大,3 495次高速列车作用下的动位移累积行程可以达到22 810 mm,说明在列车荷载持续作用下支座D3,d更容易达到磨损上限而不能再继续服役。
参照蒙特卡洛抽样模拟方法,首先模拟支座累积值,得到在3 495次高速列车作用下支座累积值的模拟结果N1,us如图8(a)所示,可以看出各次列车荷载作用下的累积模拟值同样呈现出均匀随机分布特性。进一步计算其均值,为2.848 mm,十分接近实测值的平均值2.904 mm。此外,将模拟与实测累加概率进行对比,如图8(b)所示,可以看出两者的累加概率基本一致,验证了抽样模拟方法的准确性。
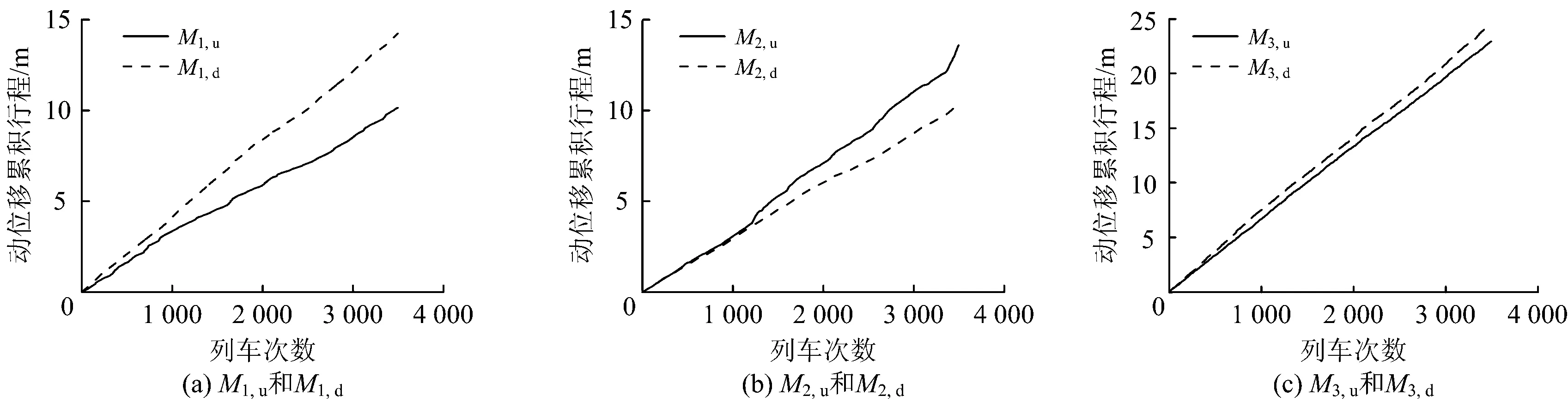
图7 各支座累积行程的计算结果
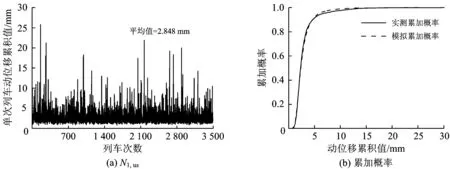
图8 N1,us的模拟值及累加概率对比结果
进一步模拟支座累积行程,即将Ni,us和Ni,ds按列车次数先后顺序依次进行累加,得到累积行程的模拟值Mi,us和Mi,ds,并与实测值对比,如图9所示。从图9可以看出:模拟值呈现出随列车次数增加而线性增加的规律;模拟值与实测值的线性增长速率基本一致,进一步验证了抽样模拟方法的准确性。
3.2 基于支座失效概率的支座磨损状况安全评估
支座累积行程Mi,us和Mi,ds的数值反映着支座在服役期间的磨损程度。若在服役期间,南京大胜关长江大桥上的盆式橡胶支座累积行程超过磨损上限,则支座不能再继续服役使用。在复杂服役环境下,球型钢支座可能会因为达不到设计使用寿命而提前坏掉,因此有必要对球型钢支座的磨损状态进行安全评估。
各支座在设计使用寿命内不能完成其使用功能的失效概率为
Pf=P(Mi,us>[Mi,us])
(2)
或Pf=P(Mi,ds>[Mi,ds])
(3)
其中,

图9 各支座累积行程模拟值和实测值
式中:Pf为在设计使用寿命内支座累积行程超过磨损上限的概率值,即失效概率;Mi,us和Mi,ds分别为支座Di,u和Di,d在设计使用寿命内的模拟累积行程;[Mi,us]和[Mi,ds]分别为支座Di,u和Di,d的磨损上限值;Ni,us(j)和Ni,ds(j)分别为Ni,us和Ni,ds内的第j个值;J是在支座设计使用寿命内的列车次数。
对于J的具体取值,若支座设计使用寿命为15 a,且在2013年内列车的统计总次数是84 343次,则J=15×84 343=1 265 145(次)。
需要指出的是,统计变量Mi,us和Mi,ds的累加分布函数是未知的,因此需要事先确定其累加分布函数。
利用式(1),对Ni,us和Ni,ds值进行蒙特卡洛抽样,抽样总个数为1 265 145。由于GEV分布的单调递增特性,得到1 265 145个Ni,us值和1 265 145个Ni,ds值,分别对其求和,得到1个Mi,us值和1个Mi,ds值。将此步骤重复K次,可得到K个Mi,us值和K个Mi,ds值。参照3.1节累积值的累加分布函数确定方法,对K个Mi,us值和K个Mi,ds值进行概率统计分析,确定统计变量Mi,us和Mi,ds的累加分布函数。需要指出的是,K值不能太小,以保证Mi,us和Mi,ds能够体现出平稳的概率统计特性。
由图7已知,各支座累积行程随列车次数呈现出不同的线性增长速率,且以M3,d的线性增长速率最快,因此以支座D3,d为分析例,对其在设计使用寿命内的磨损状态进行安全评估。具体步骤如下。
(1)首先利用式(1)对累积值N3,d进行蒙特卡洛抽样模拟,模拟时间长度为15 a,共得到1 265 145个模拟值N3,ds。
(2)将所有的模拟值相加,得到支座累积行程的1个模拟结果M3,ds。
(3)对支座累积行程模拟100次,得到100个模拟结果M3,ds,如图10所示。
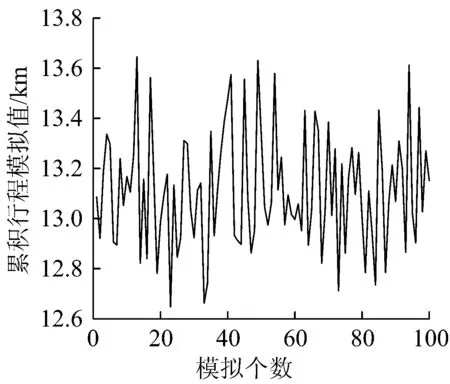
图10 支座D3,d累积行程模拟值M3,ds
(4)利用概率统计学方法,计算100个模拟值M3,ds的累加概率,并选用Normal分布、GEV分布和Weibull分布进行参数拟合,拟合结果如图11所示,可以看出GEV分布与M3,ds的累加概率特性最为吻合,因此选用GEV分布作为M3,ds的累加分布函数。
(5)由于球型钢支座的磨损行程上限值仅与聚四氟乙烯板有关,而与所施加荷载无关,因此球型钢支座的磨损行程上限值采用已有研究成果中的试验值,即已有研究表明聚四氟乙烯板的磨损上限值约为18 km[5],因此取磨损上限值为18 km;
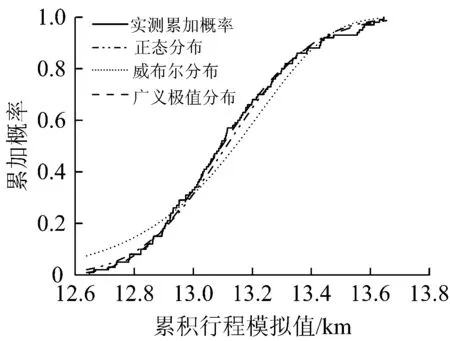
图11 M3,ds的累加概率及拟合结果
(6)利用式(3)计算得到支座D3,d的失效概率Pf为0,说明在5%的显著性水平条件下支座D3,d能够在设计使用寿命内完成其使用功能。
(7)已知其余支座动位移累积行程随列车次数的线性增长速率均小于D3,d的线性增长速率,可推知其余支座在设计使用寿命内亦能完成其使用功能。
4 结 论
(1)单次列车通过时,各支座累积值的监测结果均呈现出均匀随机分布特性,且下游侧第3个球型钢支座D3,d的动位移累积平均值最大,为7.020 mm,上游侧第1个球型钢支座D1,u的动位移累积平均值最小,为2.904 mm。
(2)采用GEV分布能够较好地描述支座累积值的累加概率特性,各个球型钢支座的动位移累积行程与列车次数之间具有明显的线性相关特性,且各个球型钢支座的动位移累积行程呈现出不同的线性增长速率,下游侧支座D3,d动位移累积行程的线性增长速率最大,在3 495次列车作用下动位移累积行程可达到22 810 mm,说明下游侧支座D3,d更容易达到磨损上限而不能再继续服役。
(3)利用GEV分布对支座动位移累积值和累积行程进行蒙特卡洛模拟,得到的支座动位移累积模拟值与实测值的累加概率基本一致,支座动位移累积行程模拟值与实测值的线性增加速率吻合度较好。提出了基于失效概率的支座累积磨损状态安全评估方法,评估结果表明所有球型钢支座在设计使用寿命内均未达到磨损上限。
