由一道高考函数题引发的思考
2019-02-18广东省饶平县第二中学515700郑道雄
广东省饶平县第二中学 (515700) 郑道雄
纵观近年来的全国高考数学试卷,函数题目经常以压轴题出现,其特点是以基本初等函数为载体,利用方程、不等式、数学建模与导数、代数推理等知识点交汇,考查函数五大性质的应用、不等式问题和函数方程思想、数形结合思想、分类与整合思想、化归与转化思想等.因能起到区分考生层次、选拔人才的作用,此类题深受广大一线师生的关注,但是该题考查方式灵活,所蕴含的思维量比较大,因此即使解题工具众所周知,不少教师对函数导数题如何备考也有无所适从的感觉,很多学生也同样是“一听就懂,一讲就会,一做就错,一考就乱”.他们最大的困惑是:好的解题思路是从哪里来的?解题的工具和大致方法知道,思路却不清晰,不知该选哪一种方法.也就是说,在面对“山重水复疑无路”的困境时,如何找到“柳暗花明又一村”的途径,是师生最需解决的问题.下面以2018年全国卷Ⅰ卷理科数学的函数压轴题为例,谈谈对此类题的一些思考.

(1)讨论f(x)的单调性;

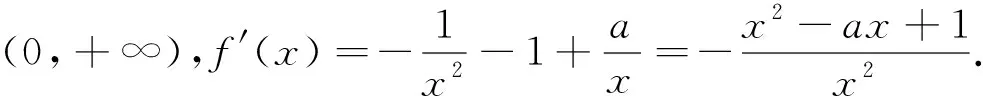
①当(-a)2-4×1×1≤0,即-2≤a≤2的时候,x2-ax+1≥0恒成立.

②当a<-2时,由于x>0,得-ax>0,又x2+1>0,所以x2-ax+1>0,此时f′(x)=
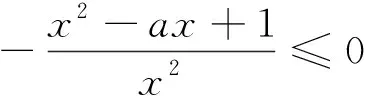

此小题考查的是函数的单调性,而利用导数这个重要工具来解决函数单调性和值域是在高中阶段最常见的.一般而言,函数求导后,再讨论导函数的正负,从而得出函数的单调性;研究函数的单调性的时候一定要在定义域里面研究.
所以在解答这个小题的过程中,有几个关键点需要考生注意.
第一,关注分类,还原讨论的层次性.
分类与整合思想是高考必考的思想方法,而且常常落脚于函数与导数,不论是对函数单调性的讨论,还是在研究函数其他性质的求解过程,总是避免不了进行分类讨论.分类与整合思想是有思维层次性的,体现在分类标准的确定上,即怎么分类讨论.第(1)题我们要讨论的是函数f(x)的单调性,从而转换为讨论导函数f′(x)在哪些区间大于零,在哪些区间小于零.而f′(x)的正负又取决于y=x2-ax+1的正负.而部分考生便无法完整分类讨论参数a的几种情况,或者说不知道分类讨论的依据是什么,而导致讨论出错.
第二,体现思维,从区间入手求解.
第(1)小题最终转换为讨论二次函数y=x2-ax+1的正负,实际上,很多难度大、思维复杂的函数题目,到最后都是转换为研究二次函数在区间上的值域问题.而二次函数在区间上的值域问题基本上就是固定的几种情况:①固定区间动对称轴;②固定对称轴动区间;③区间随对称轴改变而改变.这几种情况都离不开讨论对称轴与区间的关系,即只需讨论对称轴是否落在区间里面即可,其实质就是研究函数在给定区间里面的单调性,从而得到函数的值域.所以,必须关注函数图像的开口方向、对称轴.
第三,揭示本质,倡导数形结合思想.
应根据代数问题具有的几何特征,发现数与形的关系.在教学的过程中,教师应该详细准确的画出需要的函数图像,引导学生全方位思考,考虑问题要全面,注意是否存在一些特殊的情况.做到分类讨论既要全面,更要细致.
考生不难发现函数y=x2-ax+1开口向上,很多考生会画出函数的大致图像,而大部分同学此时画出来的图像和x轴会有两个交点,这是平时在利用图像解决同类问题时所形成的一种习惯.从而忽略了本题分类讨论中重要的一种特殊情况,函数y=x2-ax+1的图像与x轴只有一个交点或者没有交点的情况,即(-a)2-4×1×1≤0,-2≤a≤2的时候,此时y=x2-ax+1≥0恒成立.
第四,重视逻辑,另辟蹊径进行讨论.
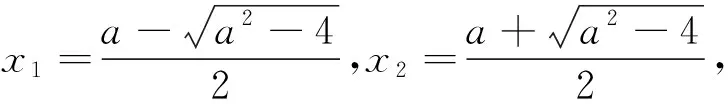



显然这跟函数单调性有关,问题变成证明函数g(x)=lnx-x在(0,+∞)上单调递减.

这种解法利用单调性来证明,感觉非常完美,可是为什么会行不通?没有办法得到结果呢?
上述解题方法错在不等式lnx2-x2 事实上,当x1,x2中的一个确定时,另一个也就确定了,因为x1,x2满足x1x2=1. 此处错在没有分析出x2的真正取值范围,其实由上述分析过程可以判断出x2>1,这是本题的另一个难点. 本题最大的难点在于不等式中出现x1,x2两个变量.近几年在高考试题的函数压轴题中,经常出现含有两个变量的不等式证明问题.面对两个变量学生会感觉无从下手,造成找不到解题的突破点.而解决这类问题的策略通常有两种,第一种当两个变量可以分离时,根据其两边结构构造函数,利用单调性证明不等式,例如思考1当中的解法.第二种是当两个变量分离不开时,可以通过作差或作商等策略将两个变量划归为一个变量,再构造函数,利用函数单调性进行证明.例如思考2中的解法即是如此. 此题带给我们的启示是,函数、方程、不等式可谓是“一胞三胎”,通过函数的图像可将它们紧密地结合在一起.要善于从函数的高度理解方程和不等式的问题,也要善于利用方程和不等式的知识解决函数问题. 2018年高考第21题再次提醒我们,函数思想有助于弄清中学数学脉络,数形结合主线可理清数学整体结构,函数问题有利于提升直观想象素养.因此,复习时要思考并重视下面几点: 第一,复习函数与导数时,教师如何建构整个模块的知识体系网络结构.知道复习的过程中什么该讲,什么不该讲,什么先讲,什么后讲,从而做到循序渐进、由浅入深,并揭示知识间的内在联系.基础知识的复习要在建构知识体系逻辑网络结构上下功夫,以知识体系带动数学的基础知识、基本技能和基本方法,从而做到纲举目张,疏而不漏. 第二,如何站在学科整体高度上,把握函数及其他模块知识的横向关系,多角度解构数学的本质.全国卷的解答题中,对函数性质的考查要求较高,尤其涉及分类讨论,数形结合等.因此在复习过程中,立体交叉地选择例题及训练题的配备. 第三,如何有效地提升学生的计算能力.压轴题中的函数题不但思维量大,计算量也很大.要让学生静下心来,将运算进行到底.但不管哪一道例题,要养成一个习惯,那就是在例题讲解完成后一定要及时小结,从问题类型归类到解决问题的方法进行反思和总结,使学生能“知其然”,更能“知其所以然”. 总之,要让平凡的函数复习课上出新意来,就必须通过形式多样的教学方式,让学生参与到教学活动中来.让学生动手、动脑、动嘴,让学生分析归纳,充分发挥学生的主体作用,而不是老师的独角戏.