泥沙侵蚀经验式经验系数不确定性对异重流数学模型的影响

张维凯,胡鹏

(浙江大学 海洋学院,浙江 舟山 316000)

泥沙异重流是挟沙水流遇到密度较小水体并下潜沿底部运动的水流过程。合理利用异重流排沙、减少水库淤积是水库管理部门面临的重要课题[1-2],在长江口深水航道区,底床附近聚集的浮泥层沿着床面运动的过程与异重流运动非常类似,是航道淤积一个不可忽略的重要因素[3]。国内外学者通过野外观测、实验和数值模拟对异重流研究取得了丰硕的成果[4-12]。特别地,异重流数值模拟取得了飞速进展。然而,异重流数学模型不可避免地要引用经验关系式,如泥沙侵蚀、水卷吸和泥沙沉速经验关系式等。其中,泥沙侵蚀经验关系式的准确性对数学模型的计算精度尤其重要。这是因为,异重流驱动力来自于其与环境流体之间的密度差,而泥沙侵蚀经验式的选取直接影响异重流含沙量,进而影响密度差和驱动力。然而,异重流泥沙侵蚀经验式存在很大的不确定性[13]。这主要是因为,经验关系式的率定需要大量高精度的实测数据。然而,异重流发生在水下,观测难度大,缺乏系统而大量的高精度野外及实验数据。Traer 等[14]采用基于贝叶斯定理的Metropolis-Hastings采样法(以下简称概率法),尝试对异重流泥沙侵蚀经验式进行不确定性分析。遗憾的是,其采用的经验式Es91[15]原本是针对明渠流过程率定得到的。尽管Es91公式与经典的异重流泥沙侵蚀经验式在表达形式上存在一定程度的相似,但Traer等[14]仅考虑了其三个经验系数的两个(A3和N2),实际上,经验系数N1的不确定性远大于经验系数A3(见表1,两个经典的异重流泥沙侵蚀经验式之间N1相差两个数量级,而A3仅相差28%,且根据本文研究,图1中当A3=7时,占总样本数95%的N1-N2组合中N1值最大为拟合最优N1的4倍,而图2中95%A3-N2样本组合中A3最大不超过拟合最优A3值的2倍)。

1 泥沙侵蚀经验式经验系数不确定性研究方法

1.1 泥沙侵蚀经验式简介

Parker结合当时可以得到的异重流和明渠流数据,拟合了异重流泥沙侵蚀经验式Es87[16]。Garcia和Parker进一步采用连续入流异重流实验数据,拟合了经验式Es93[17]。在过去二十余年,Es87和Es93两个公式是异重流数值模拟实践中应用最为广泛的泥沙侵蚀经验式。它们可以写成如下通用公式。

(1)

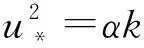
表1 Es87与Es93经验系数对比

1.2 基于贝叶斯定理的Metropolis-Hastings采样法

用Data指代实测值(即与异重流有关的u*,ω,Rp,Es等实测数据),用m指代经验系数,m=(N1,N2)或(A3,N2),用P(m/Data)表征给定实测数据前提下,经验系数取值的概率。根据贝叶斯定理,有[18]:

(2)

其中,下标j表示经验系数样本的序号,n为总样本数(本文n=15万),P(m)为先验分布(即无实测数据条件下,经验系数取值的概率),P(Data/m)为似然函数(即,对于给定的经验系数取值,经验公式计算值与实测值之间的拟合程度)。

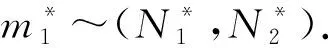
(3)

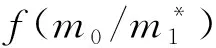
2 经验系数的样本分布

2.1 N1N2的样本分布

由表1可知,Es87和Es93式中A3的取值分别为整数7和5。本文分别取A3=3,4,5,6,7五种情况,应用概率法对N1和N2进行采样。然后使用1.2节所述方法对所有样本进行频次统计,并进一步得到总样本数25%、50%、75%、95%的N1和N2样本所在的区间范围如图1所示。若区间范围小,则说明此时系数的不确定性小。图1中不同的A3取值时,线与线的交点所在位置为样本中出现频次最高的N1和N2取值。可以看出,N1值随着A3的增大而迅速减小,而N2取值与A3相关性不大。A3取值从3到7变大时,N1的同比例样本区间范围先变小后变大,当A3=4时,25%、50%、75%、95%样本N1所在的区间相比A3取其他值时明显较小。故本文第3节中研究经验系数不确定性对数学模型的影响时,采用A3=4时的经验系数样本。

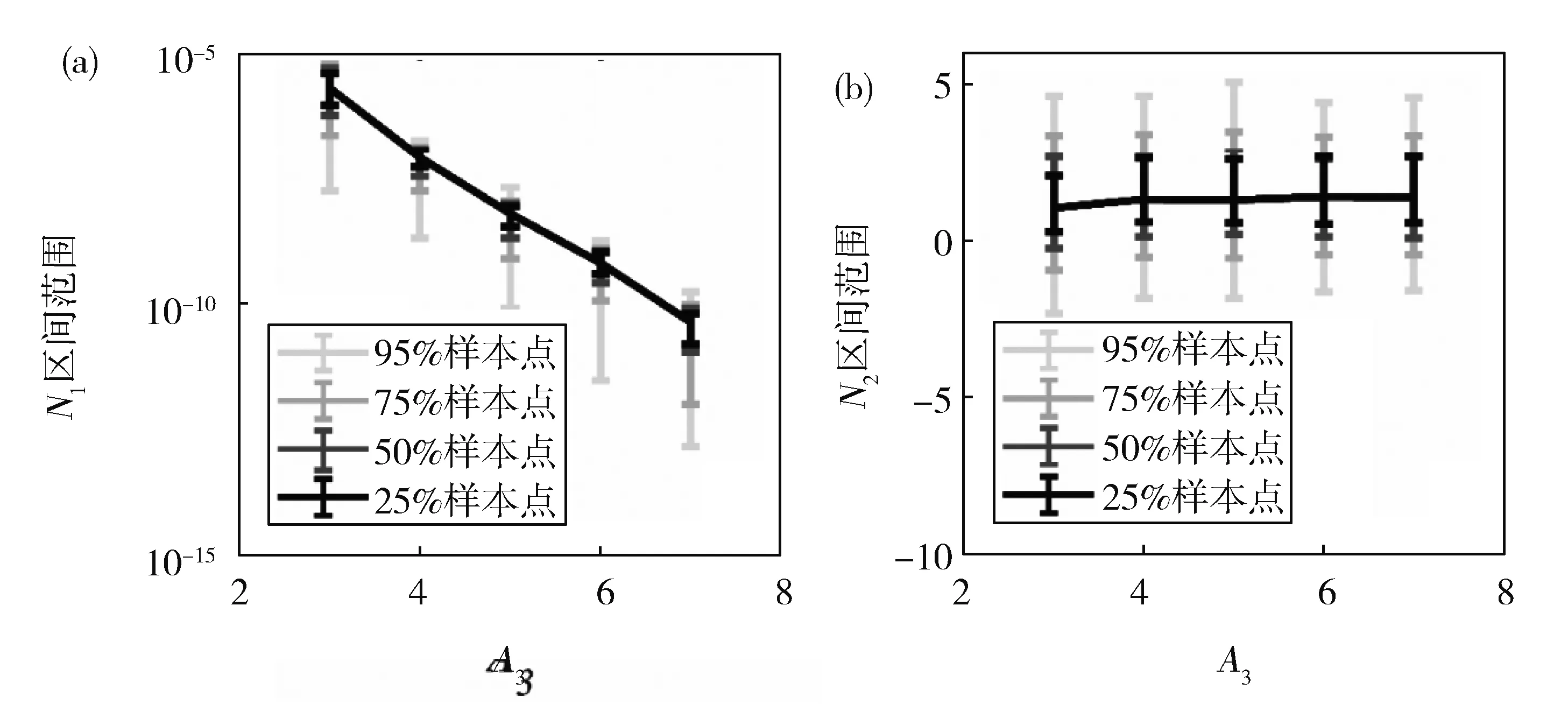
a:Interval of N1,b:Interval of N2Fig.1 Interval of different proportions of empirical coefficients N1 and N2.a:N1样本区间范围;b:N2样本区间范围图1 经验系数N1和N2不同比例样本所在的区间范围

图2a展示了A3=4时概率最大系数组合([N1,N2]=[8.4×10-8,1.32])与实测数据的拟合图像,其中实测数据来自Garcia和Parker所做异重流[17]。图2b为原Es93公式的拟合图。可以看出,概率法得到的最大概率系数组合,可以以更高的相关系数拟合实测数据。

(a) A3=4,The empirical formula of the maximum probability combination of N1 and N2obtained by probability method;(b)original empirical formula Es93Fig.2 Comparison between formula fitted by probability method and original empirical formula.(a)A3=4时,概率法所得N1和N2最大概率组合经验关系式;(b)原Es93经验式图2 概率法拟合的经验式与原经验式

2.2 A3N2的样本分布

为了与Traer等[14]的工作保持一致,给定N1=1.3×10-7,对A3-N2系数进行采样。图3为A3和N2不同比例样本区间范围,其中概率最大样本[A3,N2]=[4.10,1.28]。颜色由深至浅,依次为25%、50%、75%、95%样本的区间范围。在N1=1.3×10-7时,占总样本95%的A3-N2取值组合中,A3和N2的区间范围分别是概率最大A3-N2值的[23%,195%]和[13%,468%]。

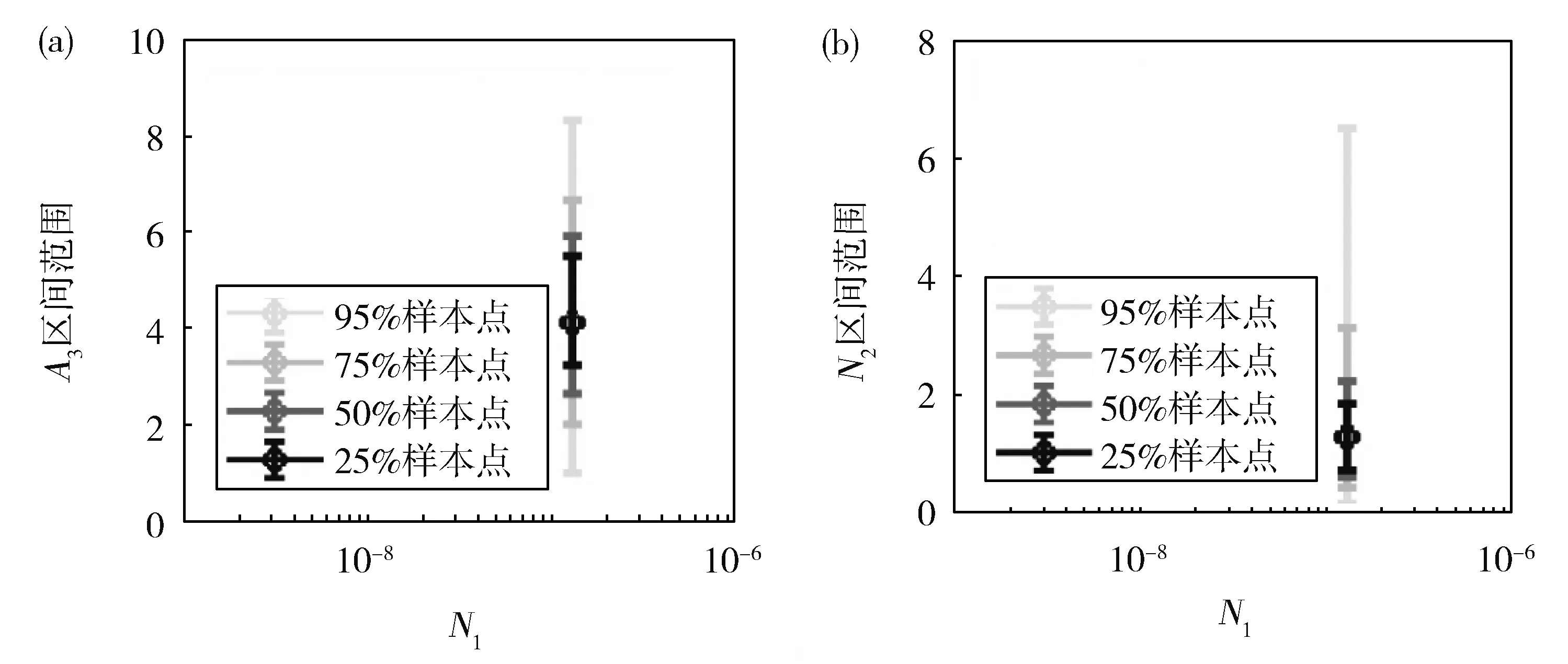
Fig.3 Interval of different proportions of empirical coefficients A3 and N2. note:N1=1.3×10-7图3 经验系数A3和N2不同比例样本所在的区间范围。注:N1=1.3×10-7时

图4a显示了本文通过概率法拟合得到的概率最大系数组合与最小二乘法拟合结果[A3,N2]=[3.7,1.4]的对比情况,可以看出,本文通过概率法得到的概率最大系数组合与最小二乘法拟合结果相近,都能够以较高的相关系数拟合实测数据。

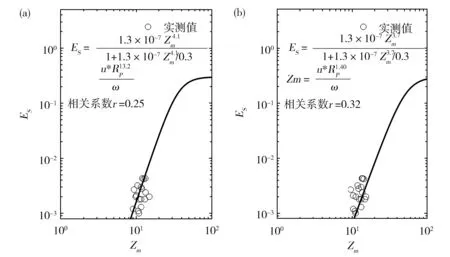
(a)probability method；(b)the least square methodFig.4 Comparison between the empirical formula fitted by probability method and the least square method (a)概率法;(b)最小二乘法图4 概率法拟合的经验式与最小二乘法拟合的经验式对比

3 系数不确定性对数值模拟的影响

3.1 异重流层平均四方程数学模型

基于恒定流假设、忽略地形冲淤反作用后,恒定的层平均异重流水沙混合物质量、动量、泥沙、湍动能守恒可以用以下四个方程表示(以下简称四方程模型)[20-21]:

(4a)

(4b)

(4c)

(4d)

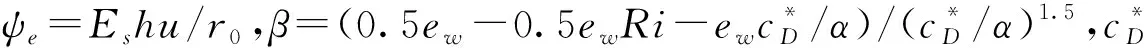
3.2 N1N2组合对异重流模型的影响分析

参考Glas等[24]的敏感性分析方法(将不同比例的经验系数样本输入模型，探讨计算结果区间的相对大小)，将N1-N2样本值输入四方程模型,计算异重流过程,并以x=100 m断面为例,将计算所得水力参数的范围(2.76 m≤h≤3.73 m;0.7 m/s≤u≤0.92 m/s;2.11×10-3≤c≤5.94×10-3)分为50等份,作频次统计,如图5所示。计算水力参数的范围越大,N1-N2不确定性对异重流计算结果的影响就越大。从图5可以看到,水力参数最大值和最小值频次较高。比如,厚度区间2.76 m～2.78 m的频次为57 380,占比约40%;厚度区间3.70 m～3.73 m的频次为16 090,占比11%。其他厚度区间占比普遍低于3%。计算速度(图5b)和浓度(图5c)也有类似的现象。

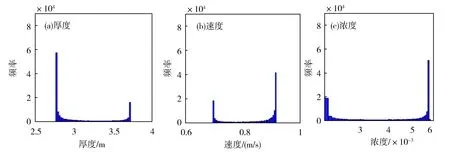
a:thickness,b:velocity,c:concentration. note:A3=4Fig.5 Frequency statistics of the water hydraulic parameters in x=100 m sectioncalculated by turbidity current four equation model with N1-N2a:厚度;b:速度;c:浓度。注:A3=4图5 N1-N2样本代入四方程模型计算所得异重流水力参数在x=100 m断面的频率统计

为解释这一现象,将N1样本范围[1×10-9,2×10-7]、N2样本范围[-2,5]等分为100份,得到10 201个N1-N2组合:输入四方程模型,得到10 201组计算结果,并取x=100 m断面处计算结果作等值线,如图6;输入公式(1)得到10 201组Es计算值,做等值线如图7。以图6a为例,根据厚度等值线疏密程度,将N1-N2平面分为3个区域(区间Ⅰ的N1和N2均较大、异重流厚度为2.76 m～2.8 m、范围较窄,区间Ⅲ的N1和N2均较小、厚度范围为3.7 m～3.73 m、范围较窄,区间Ⅱ位于区间Ⅰ和Ⅲ之间、厚度为2.8～3.73 m、范围较宽)。当N1-N2取区间Ⅰ样本值时(该区间样本总数为64 747),计算所得Es较大(图7),相应计算异重流厚度均较小、基本和最小值区间2.76 m～2.78 m范围重叠,占比达45%。类似地,区间Ⅲ的N1-N2值输入四方程模型计算异重流厚度均较大、接近厚度最大值区间,占比达11%。异重流速度和浓度满足类似的规律,不再赘述。

Fig.6 Equivalent line diagram of the water hydraulic parameters at the x=100 m section on the N1-N2 plane. a:thickness,b:velocity,c:concentration.图6 N1-N2平面上计算异重流水力参数在x=100 m断面的等值线图:a:厚度;b:速度;c:浓度

note:A3=4,u*=0.02 m/sFig.7 Contour line of Es on N1-N2 plane and the N1-N2 sample distribution注:A3=4,u*=0.02 m/s图7 N1-N2平面Es的等值线与N1-N2样本分布图。

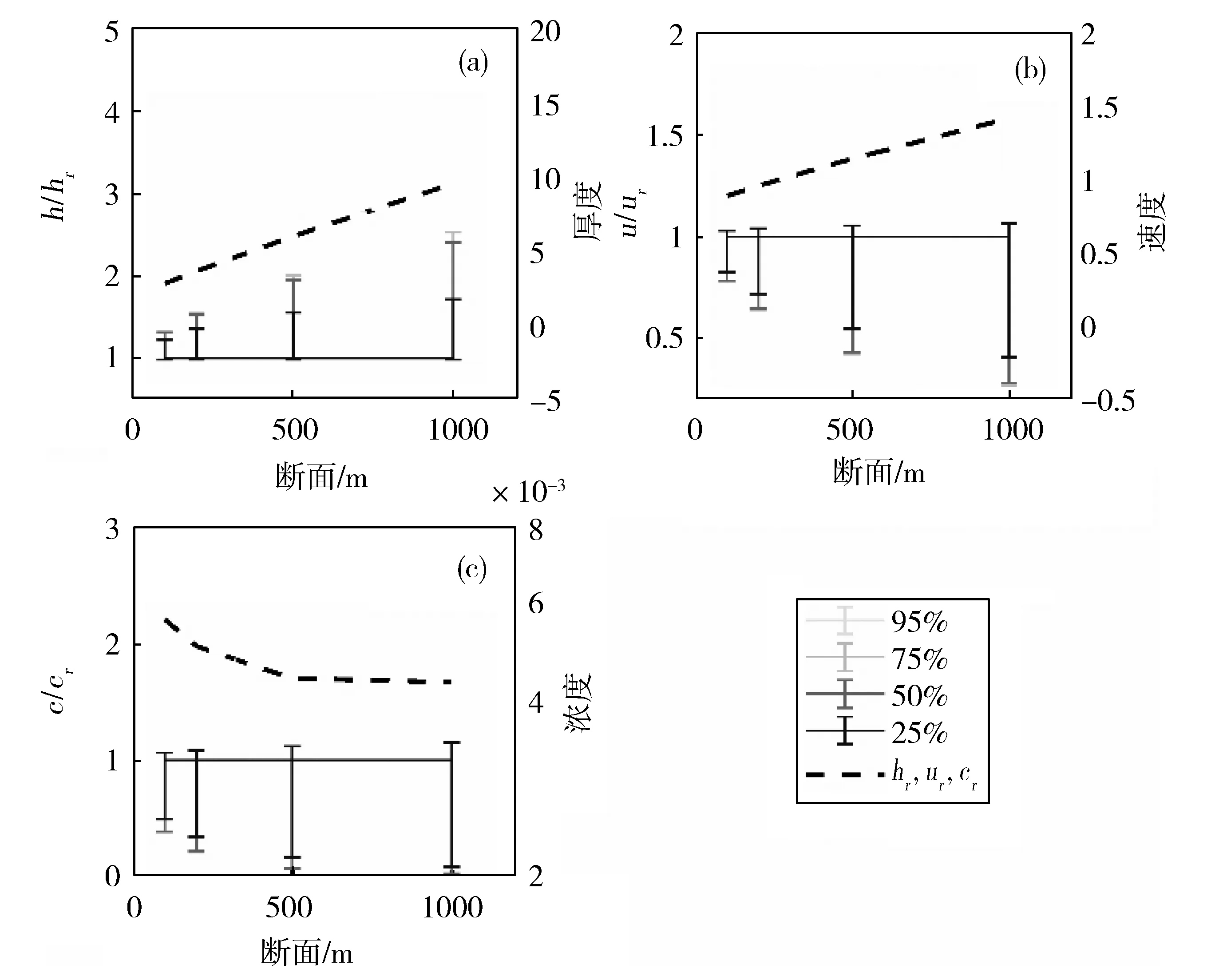
将概率最大N1-N2系数值(即频次最高取值)输入数学模型,计算所得各断面水力参数分别记为hr、ur和cr(以下简称标准值)。将N1-N2系数样本值输入数学模型计算所得水力参数(h、u、c)分别除以(hr、ur、cr),可以定量分析经验系数不确定性对数学模型计算结果的影响。图8给出了四个典型断面(100 m,200 m、500 m、1 000 m)上h/hr、u/ur、c/cr的范围,图中还通过颜色深浅区分了25%、50%、75%、95%样本对应的(h/hr、u/ur、c/cr)的范围。图中黑色虚线代表标准值(hr、ur、cr)随空间的变化。

从图8可知,随着距进口距离的增大,计算厚度和速度的标准值迅速增大、浓度标准值减小(图8a,8b和8c中黑色虚线)。比值(h/hr、u/ur和c/cr)的范围也随着距离增大而增大。这说明,N1-N2不确定性对计算水力参数的影响随着与进口边界距离增大而增强。在x=500 m处,25%样本计算的厚度是标准值的0.98-1.55倍、计算速度是标准值的0.55～1.05倍、计算浓度是标准值的0.17～1.11倍;到x=1 000 m处,计算水力参数与标准值之间倍数扩大至0.98～1.71(厚度)、0.41～1.06(速度)和0.09～1.16(浓度)。从图8可以看到,95%样本计算所得水力参数的范围略大于25%样本计算所得范围。比如,在x=500 m处,95%样本计算的厚度是标准值的0.98～2.01倍,仅比25%样本扩大30%;计算速度是标准值的0.42～1.05倍、仅比25%样本降低23%;计算浓度是标准值的0.07～1.12倍,比25%样本降低58%。通过上述分析,可以看出经验系数N1-N2对数学模型的计算结果影响很大:概率最大N1-N2值代入数学模型可能低估异重流厚度、高估异重流速度和浓度。

(a)thickness;(b)velocity;(c)concentration.Fig.8 Interval of turbidity current water hydraulic parameters calculated by different proportions of N1-N2.(a)厚度;(b)速度;(c)浓度图8 不同比例N1-N2样本计算的异重流水力参数在四个断面的区间范围

3.3 A3N2对异重流模型的影响分析

将A3-N2样本输入四方程模型,计算异重流过程,并以x=100 m断面为例,将计算水力参数的范围(2.76 m≤h≤3.71 m;0.7 m/s≤u≤0.92 m/s;2.11×10-3≤c≤5.94×10-3)分为50等份,作频次统计,如图9所示。计算所得水力参数在x=100 m的范围与N1-N2样本在模型中的水力参数范围相近。范围相近的原因是样本值范围内,泥沙侵蚀系数Es值均取到了足够大的范围:最大接近0.3(见图7和图11),最小近乎可以忽略(见图7,最小低至5×10-9;见图11,最小低至5×10-5)。尽管如此,A3-N2样本代入四方程模型所得水力参数的频次分布情况(图9)不同于N1-N2样本所得结果(图5)。如图9所示,厚度计算结果的频次统计表现为厚度最小值频次较高,计算厚度越大,频次越低;对于计算速度(图9b)和浓度(图9c)而言,最大值频率最高,计算速度和浓度越小,频次越低。比如,最小计算厚度区间2.754 5 m～2.792 3 m的频次为38 657,占比40%。

为解释这一现象,参考前文(图6,图7),对A3-N2平面内计算所得异重流水力参数和Es的等值线进行分析,得图10和图11。以图10a为例,按照计算厚度等值线的疏密程度,选择以等值线2.79 m为界,将A3-N2平面分为两个区间:区间Ⅰ的A3和N2较大,样本总数约43 576,计算所得Es均较大(图11),相应异重流厚度范围较小、基本位于厚度最小区间(小于2.79 m,图10),频次占比达到45%。区间Ⅱ,计算异重流厚度大于2.79 m,范围较大,从最小2.79 m到最大3.71 m,可以分为40余个等份(即小区间),厚度越大,对应小区间样本总数较少。以上解释了图9a显示的厚度频次统计的规律。从图9和图10可以看到,计算所得异重流速度和浓度满足类似但相反的规律,不再赘述。

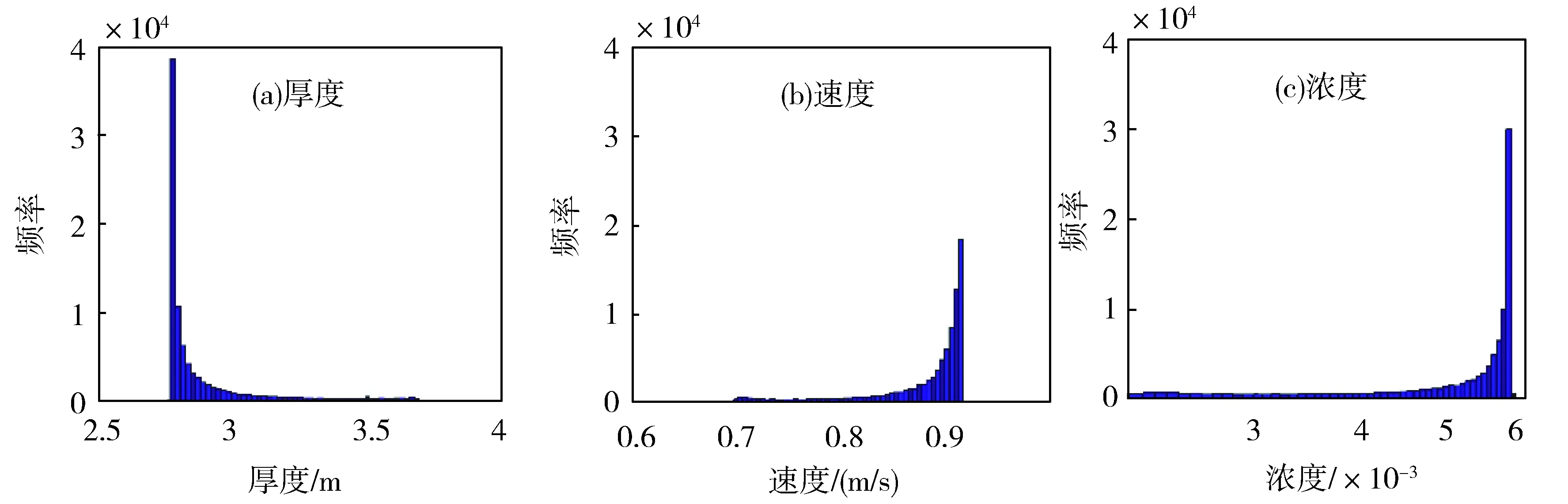
(a)thickness；(b)velocity；(c)concentration. note:N1=1.3×10-7Fig.9 Frequency statistics of the water hydraulic parameters in x=100 m section calculated by turbidity current four equation model with A3-N2.(a)厚度;(b)速度;(c)浓度。注:N1=1.3×10-7图9 A3-N2样本代入四方程模型计算所得异重流水力参数在x=100 m断面的频率统计

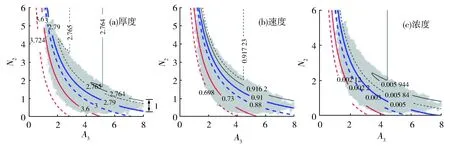
(a)thickness；(b)velocity；(c)concentration.Fig.10 Equivalent line diagram of the water hydraulic parameters at the x=100 m section on the A3-N2 plane.(a)厚度；(b)速度；(c)浓度图10 不同A3-N2值代入四方程模型计算所得异重流水力参数在x=100 m的平面等值线图。

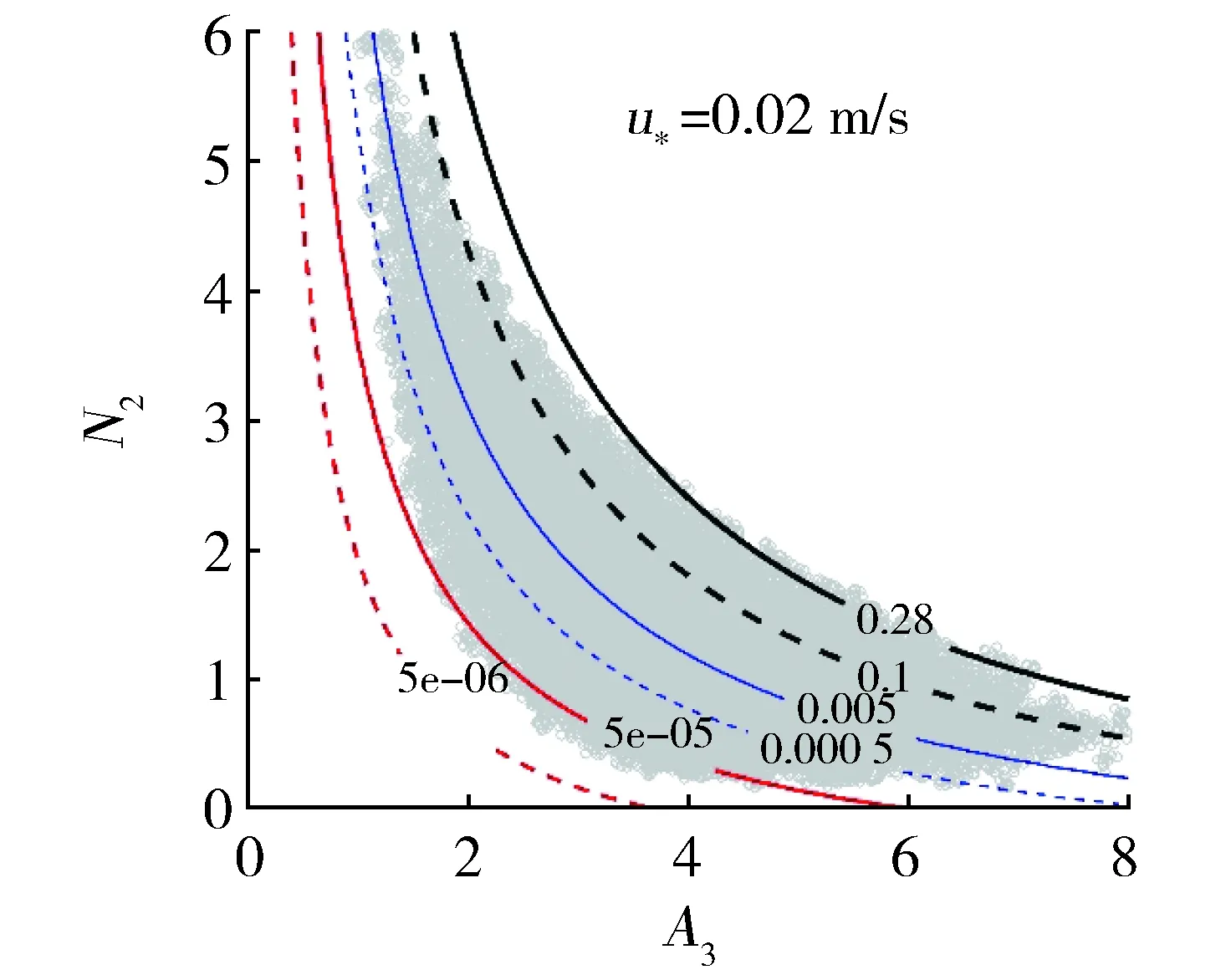
note:N1=1.3×10-7,u*=0.02 m/sFig.11 Contour line of Es on A3-N2 plane and the A3-N2 sample distribution.注:N1=1.3×10-7,u*=0.02 m/s图11 A3-N2平面Es的等值线与A3-N2样本分布图。

考察A3-N2样本对异重流模型计算结果的不确定性时,进一步采用前文(图8)相同的方法,得到图12。类似地,随着距进口距离的增大,计算厚度和速度的标准值迅速增大、浓度标准值减小(图12a,12b和12c中黑色虚线)。样本值对应计算结果(h、u、c)与标准值(hr、ur、cr)之间的差异随着距离增大而增大。然而,25%的A3-N2样本给计算结果带来的不确定性(图12),要小于25%的N1-N2样本给计算水力参数带来的不确定性(图8)。比如,在x=1 000 m处,25%的A3-N2样本对应计算厚度与标准值的差异为0.99～1.11倍(图12a),远小于25%的N1-N2样本带来的计算厚度与标准值的倍数(0.98～1.71倍,见图8a)。此外,对于A3-N2样本给计算结果带来的不确定性而言,其25%样本和95%样本对应的(h/hr、u/ur、c/cr)的范围差异较大。比如,在x=500 m处,95%样本计算的厚度是标准值的0.99～1.98倍,比25%样本扩大80%;计算速度是标准值的0.42～1.03倍、比25%样本降低50%;计算浓度是标准值的0.07～1.06倍,比25%样本降低89%。以上说明,模型计算结果对N1-N2取值的敏感度要远大于对A3-N2取值的敏感度。在建立新的泥沙侵蚀经验式时,对N1-N2取值的率定要更加注意。

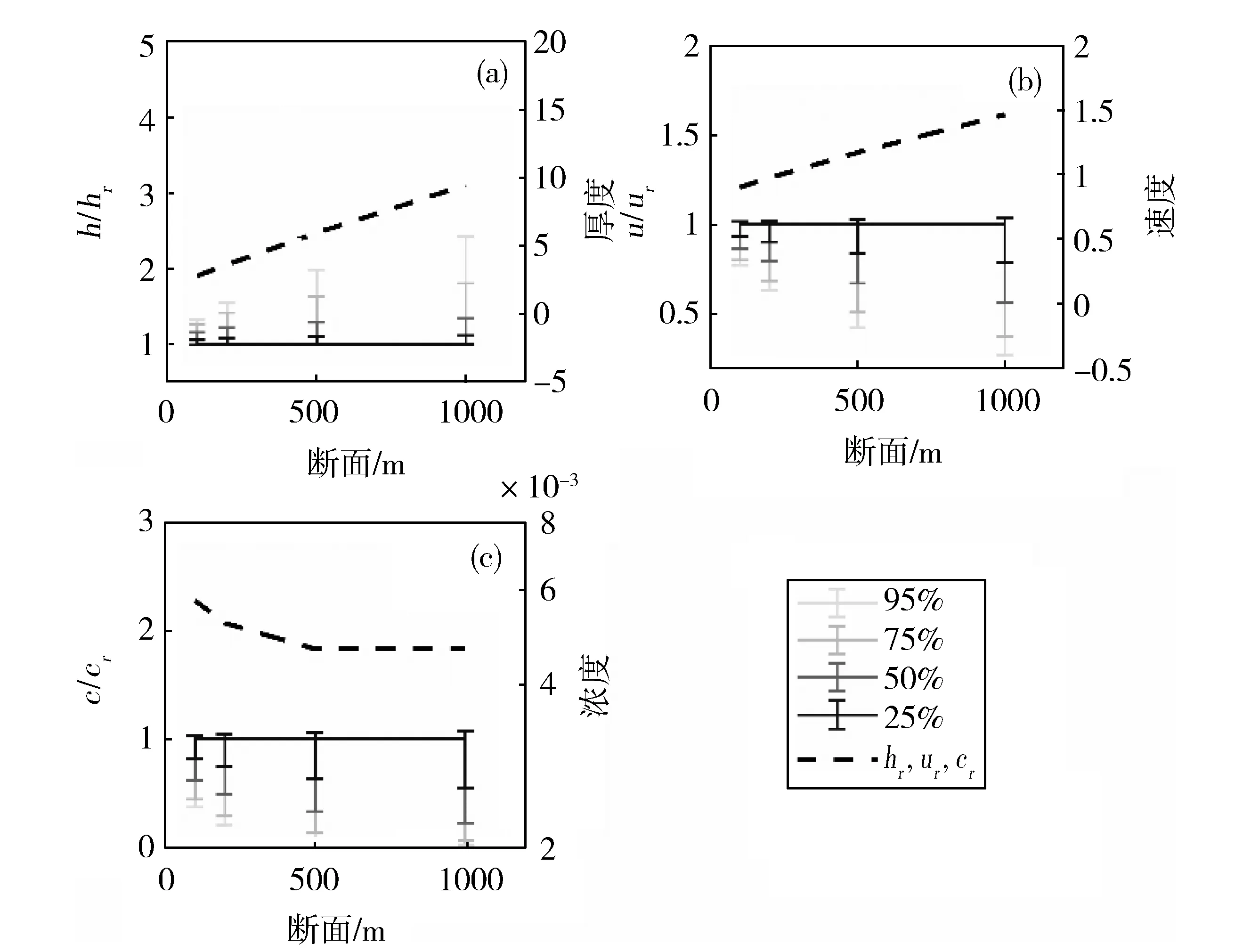
(a)thickness；(b)velocity；(c)concentration.Fig.12 Interval of turbidity current water hydraulic parameters calculated by different proportions of A3-N2.(a)厚度;(b)速度;(c)浓度图12 不同比例A3-N2样本计算的异重流水力参数在四个断面的区间范围

4 结论

本文运用基于贝叶斯定理的Metropolis-Hastings算法对泥沙侵蚀经验式经验系数(N1、N2、A3)进行了采样,得到了经验系数的大量样本,然后将这些样本输入异重流经典四方程模型,探讨了经验系数不确定性对模型的影响。结论如下:

(1)当A3=4时,95%N1-N2的样本区间比A3=3,5～7时范围更小,意味着此时经验系数的不确定性最小,当出现更多的实测数据时,A3=4所对应的经验式(图2a)能以更高的概率拟合新的实测数据。本文参考Traer令N1=1.3×10-7时,应用概率法拟合的[A3,N2]=[4.10,1.28]能够以更高的相关系数拟合实测数据,比原公式和Traer等[14]提出的系数组合更好。本文所用概率法相对于以最小二乘法为代表的传统拟合方法优势在于,传统拟合方法得到的是固定经验系数取值,而概率法得到的是大量经验系数可能取值的样本,并可以进一步分析得到其概率。一个不得不注意的事实是,通过传统方法率定的经验系数取值,在实测数据增加或存在误差时,极可能发生改变。本文通过概率法得到经验系数的大量样本,可以用于评估经验系数对数值模拟计算结果的影响,从而为数值模拟中如何选择经验关系提供一定参考。

(2)比较N1-N2和A3-N2不同比例样本计算结果在不同断面的区间范围,可以看出,计算异重流厚度、速度、浓度区间范围随运动距离的增加逐渐增大。以x=500 m处计算厚度为例,95%N1-N2和A3-N2样本计算的h/hr分别为0.98～2.01和0.99～1.98,而到了x=1 000 m处,分别扩大至0.99～2.53和0.99～2.42。采用概率最大经验系数值可能低估异重流厚度、高估异重流浓度和速度。

(3)对于A3-N2样本给计算结果带来的不确定性而言,其25%样本和95%样本对应的(h/hr、u/ur、c/cr)的范围差异较大;对于N1-N2样本给计算结果带来的不确定性而言,其25%样本和95%样本对应的(h/hr、u/ur、c/cr)的范围基本接近。这说明,模型计算结果对N1-N2取值的敏感度要远大于对A3-N2取值的敏感度。在建立新的泥沙侵蚀经验式时,对N1-N2取值的率定要更加注意。