基于工作负荷的现代有轨电车行车调度岗位设置研究

罗 文 唐光华

(广州有轨电车有限责任公司， 510030， 广州//第一作者，工程师)

随着现代有轨电车的飞速发展、网络化运营的不断完善，控制中心管辖的列车也随着增多。当调度任务量极速增长时，行车调度员可能会出现反应迟缓、错误操作的情况，给列车运营带来安全隐患。反之，调度任务量过少，行车调度员也会出现注意力不集中、单调乏味的现象，不仅降低工作绩效，还会引起行车调度配员的增加，导致成本上升、资源浪费。

因此，适当的调度工作量关系到生产效率、行车组织的安全性。为了保证列车运行安全、优化调度资源，对行车调度岗位人员的合理配置就尤为重要。

1 调度岗位工作负荷建模

1.1 调度的工作负荷定义

从人因工程学来看，行车调度岗位人员的配置应使行车调度员的工作负荷之和满足其业务负荷的需求。工作负荷是一个多维度的概念，其影响因素包括岗位要求、任务轻重、时间紧迫感，以及执行者的能力高低、努力水平和具体的个人经验。本文将工作负荷定义为在单位时间内完成职责任务所需的时间占比。即：

θ占=t任/t评

式中：

θ占——时间占比；

t任——评估期内的工作耗时；

t评——评估期内总耗时。

英国铁路和标准化局根据θ占将工作负荷划为三级，如表1所示。

表1 英国铁路工作负荷等级划分标准

1.2 调度工作负荷分类

评估行车调度员的工作负荷有3种方法：① 主观评估法，即通过检查行车调度员的主观感觉来评估；②任务分析法，即通过检查行车调度员的工作量来评估；③ 生理测量法，即通过检查行车调度员的生理变化来评估。

本文使用任务分析方法来研究行车调度员工作负荷。任务分析法将行车调度工作分为看得见的工作(台账填写，操作列车监控系统和通信协调等能够被记录和记时的工作) 、看不见的工作(监控运营列车、思考行车组织计划等不便于记录和记时的工作)和恢复工作(确保平均工作负荷强度低于80%的临界值)。

按照任务分析法，调度任务的全面分析需采用视频搜集和数据梳理两种方式，按照责任、任务和动作3个层次，来汇总和提炼调度执行的所有工作，从而获得调度的基本任务集。将调度工作的所有作业任务映射到基本任务集，即可得出了6类行车调度工作负荷子集。即将调度工作负荷分为监视负荷、思考负荷、操作负荷、记录负荷、通信负荷及其他负荷。

1.3 全日工作负荷评估及分析

本文以广州现代有轨电车行车调度的实际工作为例，搜集并整理了各类调度工作负荷对应的工作。首先，连续1周以24 h为周期，跟踪观察行车调度员的操作、通信、台账和视频回放等工作记录，以采集白班和夜班作业的所有内容(具体工作内容见表2)；然后，按单位小时计算θ占，求出每1 h时间段内的θ占平均值，最终得到调度工作负荷24 h评估结果(见图1)。

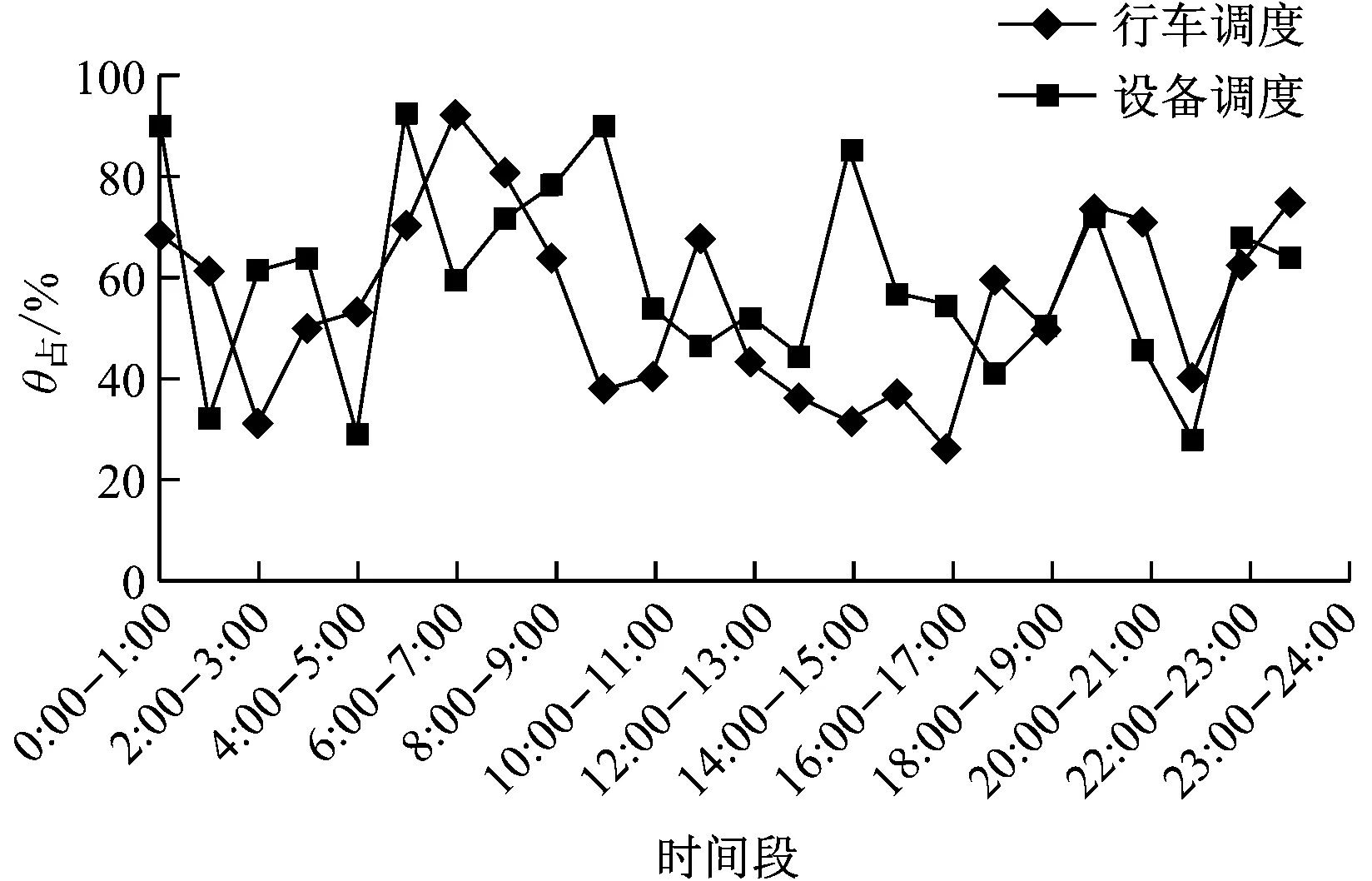
图1 连续一周调度工作负荷24 h评估结果

由图1可以看出，全天24 h行车调度的工作负荷呈现出一定的波动趋势。其中，行车调度工作最大负荷集中在早上运营前的检查、出车时段。

2 基于行车调度工作负荷的岗位配置计算

行车调度员的工作负荷与其管辖范围内的行车量密切相关。若行车调度员的工作负荷达到饱和状态的临界值，而列车数却进一步增加，则会超出行车调度员的组织能力范围，增加行车安全风险。此时的线上行车数量即为饱和量。

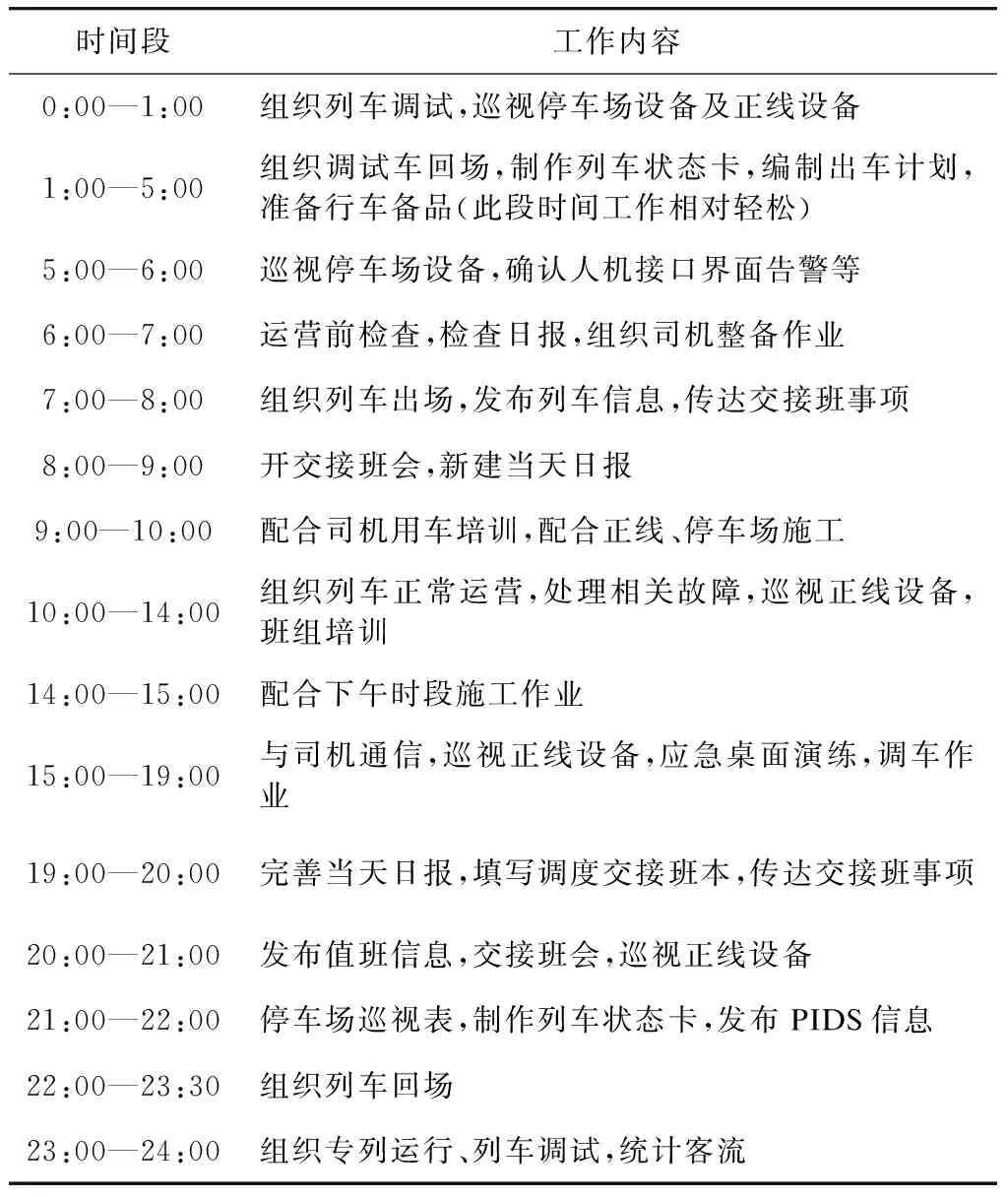
表2 行车调度员在各时间段的具体工作内容

基于行车调度工作负荷的评估，则可计算列车饱和量。通过量化评估行车调度员的日常工作负荷，可以全天候随时了解行车调度员的工作负荷状况，判断其工作忙闲程度的时间分布，并以此评估列车饱和量。

2.1 相关变量的选取

上线列车数与行车调度工作负荷密切相关。有轨电车的行车调度工作涉及到有轨电车出入场、折返、进出存车线及存车线备用等多种工况。有轨电车运转流程图如图2所示。正常情况下，有轨电车可根据预设的目的地码自动排列进路，按照运营时刻表行车。此时，行车调度员的工作是监控列车运行。但在非正常情况下，如因列车设备故障、列车冲突及交通事故等突发事件，而造成列车抽线、晚点、中断运营或改变列车运行交路时，需行车调度员人工介入进行调整。此种情况则赋予了行车调度员新的工作任务，增加了相应的工作负荷。可见，人工调整列车亦与行车调度员的工作负荷密切相关。

综合考虑，为研究行车调度员的工作负荷与运营列车之间的相互关系，初步确定行车调度员的工作负荷同运营列车数及人工调整列车数有关。在一定评估期内，工作负荷由工作耗时确定。因此将行车调度工作耗时设为因变量，将运营列车数和人工调整列车数设为自变量，并筛选适当的方法进行求解。

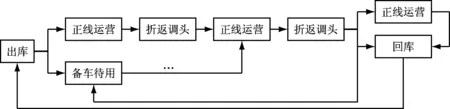
图2 有轨电车运转流程图

2.2 建立行车调度员工作负荷回归模型

2.2.1 采集变量数据

基于对行车调度员工作负荷的定量分析，结合广州有轨电车的实际运营时间，确定因变量及自变量。首先，确定评估期为为7:00—22:00，共15 h；然后，按运营列车数，分别统计同时上线4列、5列、6列有轨电车时的调度工作耗时；最后，确定不同人工调整列车数对应的调度工作耗时。对于人工调度列车数，本文只统计列车故障下调整的列车数。

2.2.2 绘制散点图

根据统计的数据进行整理，得到运营列车数、人工调整列车数对应行车调度工作耗时的散点图，如图3～4所示。

2.2.3 回归方法的选择

通过散点图可以看出，自变量与因变量间呈现明显的线性正相关关系，且自变量间高度不相关。因此，选择多元线性回归分析进行求解，由此建立二元回归模型为:

y=β0+β1x1+β2x2+ε

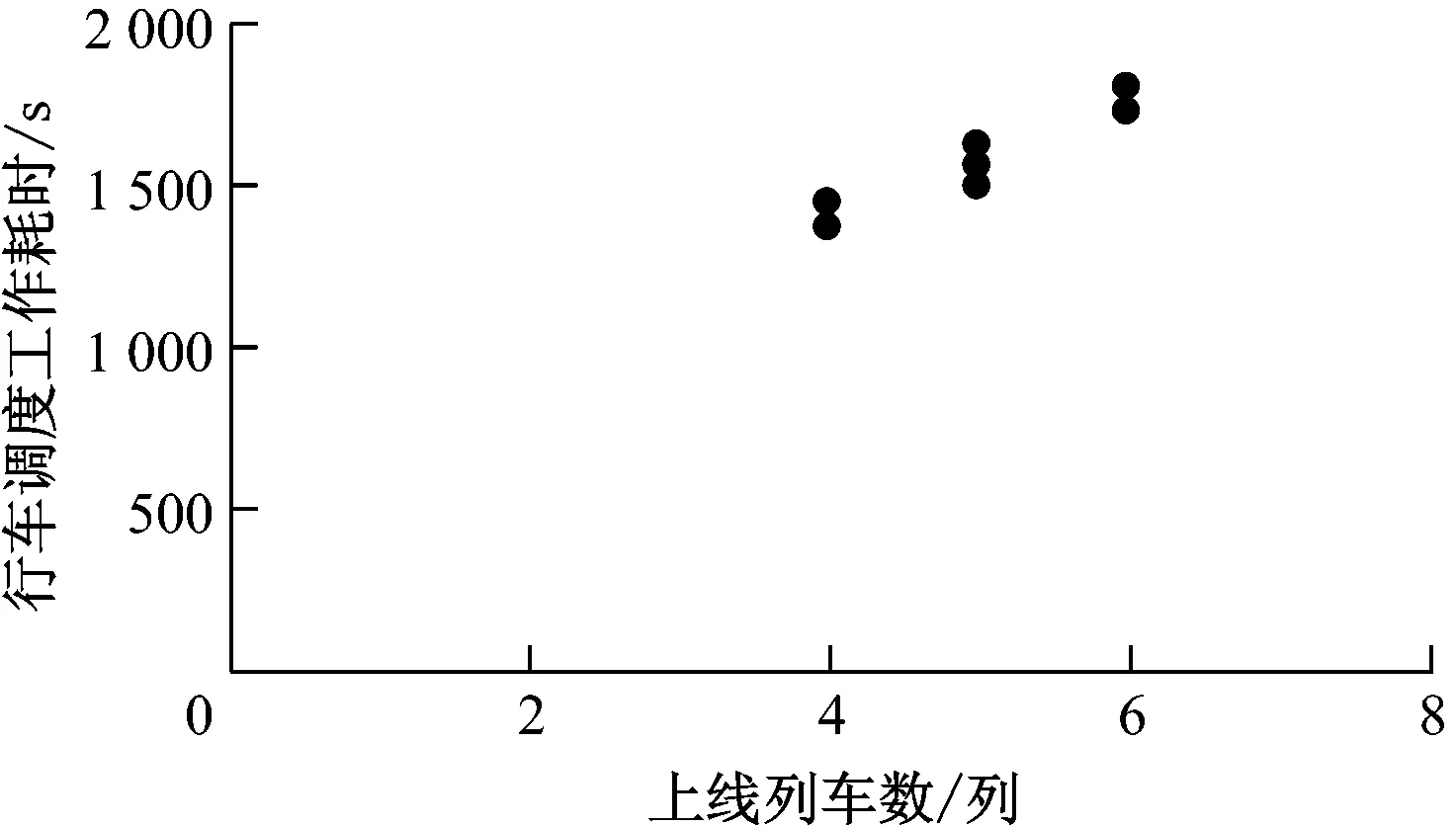
图3 不同上线列车数对应的行车调度工作耗时

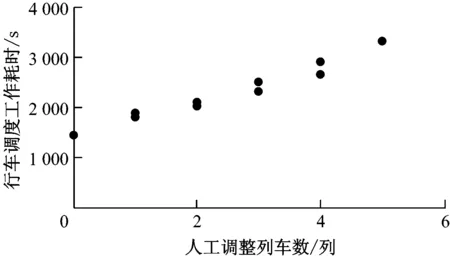
图4 不同人工调整列车数对应的行车调度工作耗时

式中：

y——工作耗时；

x1——运营列车数；

x2——人工调整列车数；

β0——回归常数；

β1,β2——分别为x1,x2的回归常数；

ε——随机误差项。

根据统计数据，进行多元线性回归分析。分析结果如图5所示。

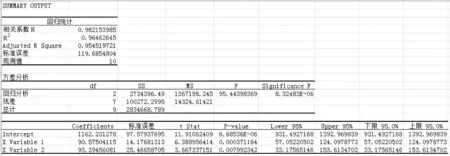
图5 工作负荷线性回归分析参数

根据图5中显示结果，相关系数R为0.982，说明上线列车数和人工调整列车数同行车调度工作耗时呈现高度正相关。故可用二元线性回归方程进行拟合。计算得到的行车调度工作耗时回归方程为：

y=90.58x1+93.39x2+1 162.23

其中，y单位为s，x1、x2单位为列。

计算得到判定系数等于96.46%。这表明在行车调度工作负荷变动中，有96.46%可由上线列车数和人工调整列车数这2个因素的变动来解释，只有3.54%的因素属随机误差。

设显著性水平α=0.05，查F分布表得F0.05(2，7)=4.74。计算得到F=95.44>4.74。因此，拒绝原假设，认为y同x1及x2有显著的线性关系。

从图6可见，所有的残差都在0附近均匀分布，且区间几乎都位于[-200 s, 200 s]之间，没有发现高杠杆点。即数据中没有强影响点或异常观测点。

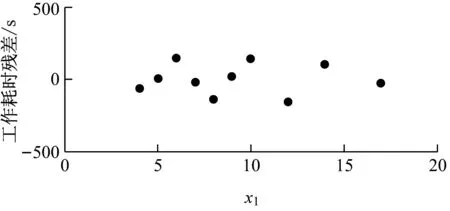
a) x1变化时

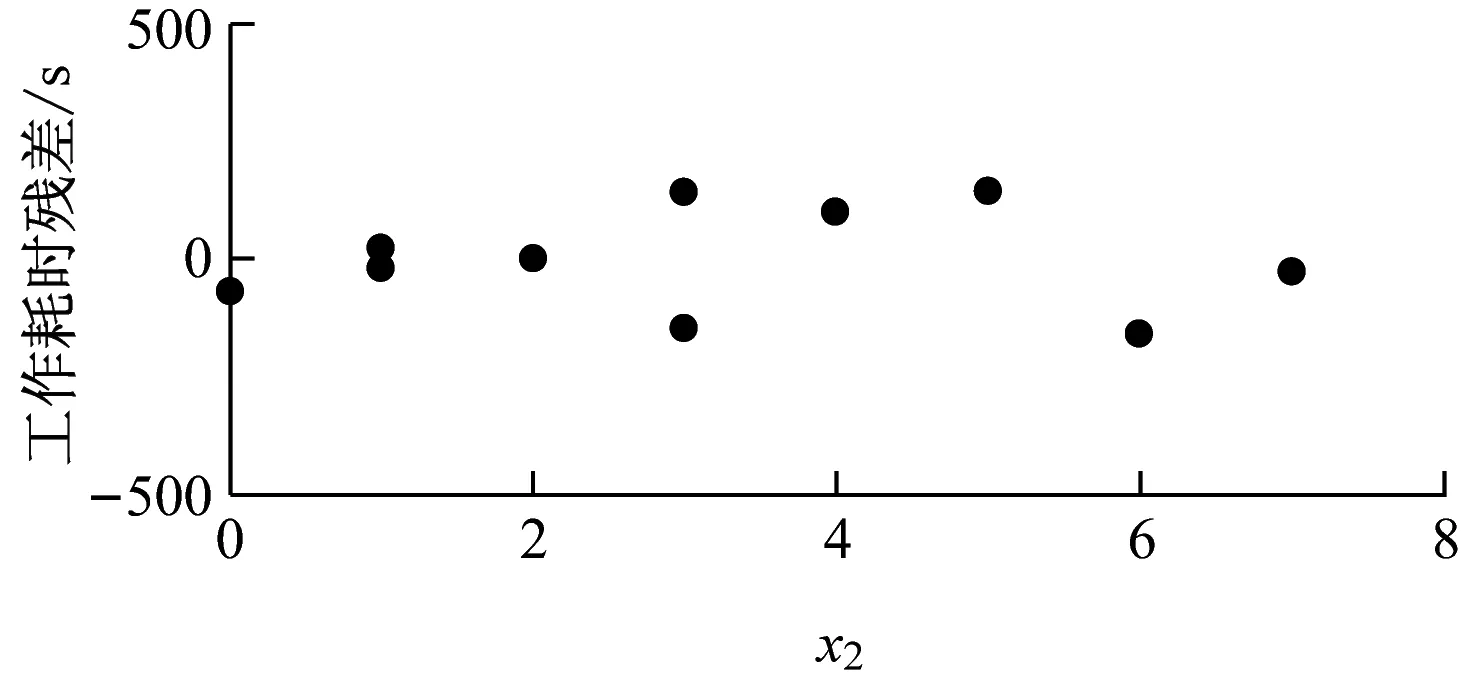
b) x2变化时

故认为行车调度工作耗时回归方程是整体显著的。

其次，设α=0.05，β1的检验统计量t1=6.39、β2的检验统计量t2=3.67，查t(检验统计量)分布表得t0.025(7)=2.36。因t1、t2均大于t0.025(7)，因此，拒绝原假设，认为行车调度工作负荷回归模型的各个回归系数是显著的。

3 结语

本文以广州现代有轨电车为例，系统分析了现代有轨电车行车调度的工作任务，借用任务分析方法建立了行车调度工作负荷模型，并进行了量化测量，以此评估行车调度的工作负荷状况。在此基础上寻找影响行车调度工作负荷的自变量，建立了多元线性回归模型，并校验了模型的准确性，对现代有轨电车行车调度岗位配员和新线规划具有一定的参考意义。