基于电子鼻系统的白酒掺假检测方法
2019-02-15马泽亮国婷婷殷廷家王志强杨方旭李彩虹李钊袁文浩
马泽亮,国婷婷,殷廷家,王志强,杨方旭,李彩虹,李钊,袁文浩
(山东理工大学 计算机科学与技术学院,山东 淄博,255049)
随着食品质量事件频发,食品安全问题已成为全球性关注的热点[1]。中国白酒具有悠久的历史,是世界上著名的蒸馏酒之一[2],在人们生活中占据重要的地位,而近年来市场上各种白酒品质参差不齐,其中不乏各种勾兑而成的掺假白酒。掺假白酒的制造及销售严重损害了消费者身体健康和财产安全。因此,构建一种快捷、直接、可靠地辨别掺假白酒的方法具有重大的社会意义。
感官品质分析是白酒品质分析常用的方法,但此类方法易受品评者的疲劳效应以及主观因素的影响,具有重复性差,主观性强等缺点,使得分析结果具有较大的误差。传统的分析检测方法有紫外可见吸收光谱法(UV-VIS)[3]、傅里叶近红外光谱法(NIR)[4]、核磁共振光谱 法(NMR)[5]; 高效液相 色谱法(HPLC)[6]、气相色谱 -质谱 联用法(GCMS)[7-8]等。虽然,UV-VIS等光谱法的检测仪器具有操作简单、检测迅速、成本低廉等优点,且近年来在酒的应用分析和质量控制有了很大的发展[9-10],但该仪器检测灵敏度低,缺乏准确的定性、定量检测能力。HPLC等色谱法由于其分离能力强、选择性好已成为应用广泛的常规检测分析方法,但耗时长、操作繁琐、且容易对样本造成破坏,无法满足对实际样本的快速准确分析的需求。
电子鼻是模仿人类嗅觉感觉机理的一种新型现代化智能分析检测仪器,近年来在化学物质和感官特性的快速测定中起着不可或缺的作用[11],利用传感器阵列获得样本“指纹信息”,经过信号处理以及模式识别后,最终得到各种溶液嗅觉的整体特征信息,实现对复杂液体的定性与定量检测,具有操作稳定可靠、运行简单、成本低廉、检测快速等特点。目前,电子鼻已开始应用在环境监测[12-13]、中药鉴定[14-16]、食品分析[17-19]等众多领域。近年来,众多国内外专家、学者在酒的风味和品质检测方面已成功开展了大量科学研究,如徐晚秀等[20]利用电子鼻对5种年份的清香型白酒酒龄进行了在线实时检测;王辉等[21]利用声表面波zNose4200型电子鼻实现了对3种香型6种白酒快速识别与分类;LUIS GIL-SHCHEZ等[22]利用电子鼻和电子舌对白酒和红酒的氧化过程进行了分析研究。众多研究表明,电子鼻具有对气体中特异性理化物质进行鉴别的能力。但利用电子鼻检测系统对不同纯度的掺假白酒进行定性和定量检测分析,国内外尚未有相关报道。
本文以掺假白酒为检测对象,以虚拟仪器为核心构建了一套电子鼻检测系统,实现了对不同纯度的掺假白酒定性和定量鉴别分析。针对电子鼻响应信号的特点,采用DWT方法对电子鼻原始信号进行预处理,随后利用PCA方法对不同纯度的掺假白酒进行定性辨别,同时采用ABC-LSSVM方法对白酒纯度进行定量预测。旨在为掺假白酒检测评价提供有力的技术支持。
1 材料与方法
1.1 材料与试剂
实验所用茅台镇原浆酒均来自淄博市大润发超市,在实验前密封保存,防止氧化变质。
1.2 仪器与设备
自主研发的电子鼻系统主要由基于LabVIEW的上位机系统、数据采集装置、信号调理电路以及传感器阵列构成,如图1所示。
1.3 试验方法
本文根据文献[23]中白酒掺假样品的制备方式,向茅台镇酱香酒里混掺工业酒精和饮用水,分别配制体积分数为100%、90%、80%、70%、60%及50%的实验样品各400 mL,平均分成20份,利用酒精计控制掺假白酒的酒精度和真酒酒精度保持一致。
打开电子鼻检测系统,设定在经过预实验确定的参数:样本气体进样速率500 mL/min,载气速率500 mL/min,检测前对电子鼻检测系统清洗时间为80 s。每次取20 mL的掺假白酒样品,置于300 mL的锥形瓶中并利用瓶塞密封,检测时间为80 s。
1.4 数据处理与分析
1.4.1 小波信号预处理
电子鼻采集回来的数据具有数据量大、高维、动态、稀疏性以及含噪声等特征,若直接进行模式识别分析,不仅加重系统工作量,还会降低识别率,因此必须对原始数据预处理,以降低冗余信息并提取关键信息。通常,对电子鼻信号进行预处理大多采用面积值、稳定值和平均微分值[24]等提取法,但此类方法获取信息量小,不能挖掘及利用全部信息,影响系统的识别效果。小波变换是为分析非静态信号而开发的,具有自适应、多尺度及“数学显微”等特点,可以有效地减小数据冗余和降噪,处理后的数据可以保持原始数据波形特征,便于后期模式识别分析。离散小波变换是小波变换在尺度及位移上离散化。
离散小波变换过程中,分解尺度和小波基函数的选择都会影响重构信号的失真度以及信号压缩比,而以往主要凭个人经验对这2个参数选取,存在主观性强等问题,因此利用波形相似系数f对DWT处理结果进行评价,公式如下:

(1)
式中:p为原始数据的数据点;q是DWT压缩重构后的数据点;cov(p,q)代表2组信号的协方差。波形相似系数f越大,则说明原始信号和压缩后信号接近程度越大。
1.4.2 基于PCA的定性辨别分析
PCA是一种多元统计分析方法,已广泛应用于电子鼻检测领域。PCA能够将相关变量转化成可以解释原始信息的多个无关变量的组合,最终在保持不丢失大部分原始数据的状况下,进行数据特征提取或分类识别。
1.4.3 基于ABC-LSSVM的定量预测模型
1.4.3.1 最小二乘支持向量机
最小二乘支持向量机(LSSVM)是基于SVM结构风险最小化基础上改进的一种新型的模式识别方法,在白酒检测领域已得到成功应用[25]。其基本原理为利用一种非线性映射,将原始数据映射到高维特征空间中,并找出一个最优超平面,建立输入及输出之间非线性关系模型。本文的LSSVM输入量是经过小波压缩后的电子鼻响应信号,输出量是白酒纯度。优化问题变为:
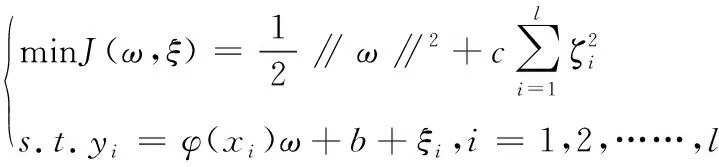
(2)
式中:c为惩罚因子,用于调整训练误差样本中的惩罚力度;b是偏差;ξi是训练样本的预测误差向量;ω是权重向量。为了解上述优化问题,需要把求解二次规划的问题转换成求解方程组问题,通过解方程组能够得出LSSVM模型:

(3)
式中K(x1,xl)是符合Mercer理论条件下的核函数,由于径向基核函数具有拟合效果好,学习能力强等优点,因此本文核函数采用径向基函数并建立LSSVM模型,其算法如下:

(4)
核参数σ和惩罚因子c是影响LSSVM模型泛化能力和预测能力的两大关键因素。核参数σ决定样本空间至特征空间的一种映射关系,惩罚因子c可以实现最小化模型复杂度和训练误差之间的均衡。因此建立LSSVM预测模型的首要任务是寻找核参数σ和惩罚因子c的最佳优化方式。
1.4.3.2 人工蜂群算法
人工蜂群算法(artificial bee colony,ABC)是一种模拟自然界中蜜蜂采蜜而设计的一种算法,通过模拟蜂群智能采蜜,交换蜂蜜源信息等过程而获得最优解,相对于遗传算法算法算法具有较强的适应性与灵活性[35]。
在ABC算法中,将蜂群分为3种:雇佣蜂、跟随蜂和侦查蜂,其中雇佣蜂和跟随蜂数量各占蜂群数量的一半,且每个蜜源在同一时间只能有一个雇佣蜂工作,因此说蜜源与雇佣蜂数量相等,用C表示,放弃蜜源的雇佣蜂转化为侦察蜂。ABC的寻优过程可以概括为:雇佣蜂依靠它们记录的蜜源位置在其邻域内确定另一个蜜源,然后将蜜源信息发送给跟随蜂,跟随蜂采用贪婪机制选择其中一个蜜源,随后依靠所选蜜源在其邻域内搜索另外一个蜜源,依次循环,最终寻得最优解。跟随蜂和雇佣蜂主要用于寻找最优解,侦查蜂则用于避免陷入局部最优问题,若陷入局部最优问题则随机搜索新解。具体步骤如下:
(1)初始化蜂群。随机生成初始化蜂群C,均匀分布在寻优空间,其中雇佣蜂和跟随蜂数量相等且为Ny=Ns=0.5C,雇佣蜂种群G={X1,X2,…,XNy},采蜜蜂个体为X={XI,1,XI,2,…,XI,M},其中i=1,2,…,Ny,A是问题解的维数,Xi的各个分量由式(5)产生:
Xi,j=Xi,jmax+rand(0,1)(Xi,jmax-Xi,min)
(5)
式中:Xi,jmax,Xi,min分别表示Xi的第j个分量的下限和上限。
(2)收益度hi的计算。收益度通过式(6)求得:
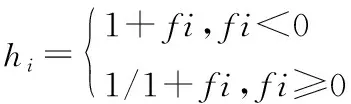
(6)
式中:fi为目标函数。雇佣蜂通过式(7)产生新的雇佣蜂Xi, 1(其中i≠C):
Xi,1=Xi+rand(0,1)(Xi-XC)
(7)
(3)计算新产生采蜜蜂个体的收益度,根据式(8)分配跟随蜂的数量,并由式(9)进行蜂群的更新:
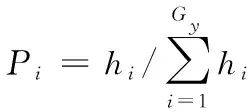
(8)
Xi,2=Xi1+rand(0,1)(Xi1-XC1)
(9)
(4)依据贪婪机制选择新蜂群。与之前的蜂群个体的收益度进行比较,收益度最大的个体成立新的蜂群。
(5)侦查蜂的生成。通过上一步后,按照式(10)转变为侦察蜂Xzi,其各个分量为:
Xzi,j=2(Xi,jmax-Xi,jmin)(0.5-rand(0,1))
(10)
(6)不满足收敛时,回到步骤2,直到循环结束为止。
1.4.3.3 基于ABC算法的LSSVM参数优化
最小二乘支持向量机,需要优化的参数主要有核参数σ和惩罚因子c,基于ABC算法的LSSVM参数优化流程如图1所示。

图1 基于ABC算法的LSSVM参数优化Fig.1 Artificial bee colony least squared-support vector machines
(1)初始化ABC算法中的控制参数:食物源的数量Ny,即雇佣蜂的数量。
(2)设置ABC算法的适应度函数,优化LSSVM的目的是获得更好的定量预测精度,因此选用的适应度函数如式(11)。

(11)
式中:Vaca是LSSVM的预测精度。
(3)初始化参数的搜索范围。核参数σ和惩罚因子c的改变均会影响LSSVM的预测性能,提前确定模型参数的搜索范围,有助于获得更好地预测精度。
为了验证ABC-LSSVM的模型对白酒纯度的预测性能,分别选择留一交叉验证算法优化最小二乘支持向量机(LOOCV-LSSVM)、遗传算法优化最小二乘支持向量机(GA-LSSVM)以及标准粒子群算法优化最小二乘支持向量机(PSO-LSSVM)与本算法进行比较分析。为了全面评估几种模型预测性能,其有效性可通过决定系数(R2)来评价,其预测精度可通过均方根误差(RMSE)以及平均相对误差(MRE)来进行衡量。评价指标公式如下:
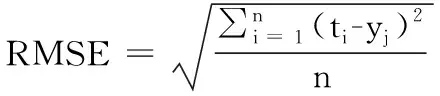
(12)

(13)

(14)
式中:n为测试样本数量,ti和yi分别是测量及预测值。R2越大预测模型越有效,RMSE及MRE越小精度越高。
2 结果与分析
2.1 小波信号预处理
由于电子鼻每检测一次就会产生6 000个原始数据,这些数据信息量大、高维、含噪声,难以直接进行模式识别分析,根据电子鼻检测信号特点,本实验利用Matlab软件平台,采用离散小波变换(DWT)进行数据预处理,分别采用Coiflets、Daubechies、haar、Symlets小波函数作为小波基函数对原始信息进行5~8层压缩分解,波形相似系数f变化情况如图2所示。对比发现,以sym4为小波基函数经6层压缩效果最好,相似系数f为0.975 6,可将6 000个数据减小至47个数据。

图2 不同压缩层数及母小波对相似系数f的影响Fig.2 Influence on similarity coefficient of different decomposition level and mother wavelet
2.2 基于PCA的掺假白酒定性辨别
利用电子鼻对每个不同纯度的掺假白酒样品分别进行连续20次平行检测,基于Matlab软件平台采用PCA对不同纯度的掺假白酒样品电子鼻检测数据进行分析。其主成分分布如图3所示,第一主成分和第二主成分的贡献率分别为63.32%和25.80%,累积贡献率达到89.12%,说明PCA很好地解释了电子鼻特征信息。从图3分类效果上来看,不同纯度的掺假白酒样品聚集在PCA图中不同区域,即不同样品之间存在较大的差异,电子鼻信号稳定性较好,6种不同纯度的掺假白酒得到了有效的区分。

图3 掺假白酒PCA结果图Fig.3 PCA Diagram of adulterated Liquor
2.3 基于ABC-LSSVM的白酒纯度定量预测
为了实现对不同纯度的掺假白酒定量预测,将6个传感器的采集信号作为自变量,白酒纯度作为因变量,建立LSSVM白酒纯度定量预测模型。利用电子鼻对每种不同纯度的掺假白酒样品分别进行连续20次平行检测,选取90个样本(每种浓度15个,共6种浓度)作为训练集,用以建立模型及优化参数。剩余的30组(每种浓度5个,共6种浓度)作为验证集,用于验证所建立模型的性能。
为了验证ABC-LSSVM的模型对白酒纯度的预测性能,分别选择留一交叉验证算法优化最小二乘支持向量机(LOOCV-LSSVM)、遗传算法优化最小二乘支持向量机(GA-LSSVM)以及标准粒子群算法优化最小二乘支持向量机(PSO-LSSVM)与本算法进行比较分析。以建模集对上述模型进行优化训练,验证集对模型预测性能进行检验,ABC-LSSVM白酒纯度预测模型如图4所示,不同参数优化方法下的LSSVM白酒纯度预测模型评价结果如表1所示。

图4 不同纯度白酒样本ABC-LSSVM数据分析图Fig.4 ABC-LSSVM data Analysis Diagram of Liquor samples with different Purity
综合以上4种参数优化方法的评价结果可以看出,LOOCV-LSSVM预测效果最差,这主要是因为LOOCV方法计算成本较高、寻优过程复杂,不能更快、更准确的寻找最优的(σ,c)参数组合造成的,从表1可以看出GA、PSO和ABC 3种LSSVM优化方法确定的预测集预测结果回归线与1∶1线都相接近,从表1可知3个LSSVM模型验证集中,预测值与真实值之间的决定系数R2均大于0.92,RMSE均低于0.03,预测性能都较好,但以MRE为评价依据,ABC优化LSSVM模型的预测精度略高于PSO和GA优化的LSSVM模型预测精度。各评价指标之间虽差距不大,但ABC优化后的LSSVM模型对掺假白酒纯度的预测精度已得到了很好地提高。这主要是因为ABC具有劳动分工和协作机制,收敛速度快、鲁棒性强且全局寻优性能优异,因此相比于PSO和GA具有更强的灵活性与适应性[36-37],能够更加准确的寻找最优的(σ,c)参数组合,因此ABC-LSSVM模型对白酒纯度就具有较高的预测能力。

表1 不同参数优化方法下的PLSR和SVM模型性能指标对比Table 1 Performance comparison of PLSR and SVM model based on different parameter optimization methods
3 结论
自行研制了一套电子鼻检测系统,并将其应用于掺假白酒的定性与定量检测中。针对传统上对电子鼻信号进行预处理大多采用面积值、稳定值和平均微分值等提取法,提取信息量小,不能挖掘和利用全部信息等缺点,本文选用了DWT方法对电子鼻信号进行特征提取,然后采用PCA和LSSVM分别对白酒纯度进行定性和定量辨别。LSSVM参数是影响预测效果的重要因素,提出了一种基于ABC的LSSVM优化方法。同时,为了验证ABC-LSSVM的模型对白酒纯度的预测性能,分别选择LOOCV-LSSVM、GA-LSSVM以及PSO-LSSVM与本算法进行比较分析,结果表明,ABC-LSSVM预测模型对掺假白酒定量预测效果最好。电子鼻系统能够对掺假勾兑白酒样本进行准确的定性和定量分析,该研究成果将为白酒纯度检测方面提供新的技术支撑。
