高层剪力墙建筑结构的多目标优化

李双龙 梁晓东 胡守营 王传甲

(奥意建筑工程设计有限公司，广东深圳 518031)

0 引言

随着我国经济和社会的发展，城市人口密度持续增长，新增用地日益紧张，高层建筑的发展已经成为历史的必然和时代的潮流［1］。由相关数据统计可知，我国已建的高层建筑中80%是住宅，而在这些高层住宅中钢筋混凝土剪力墙结构占比在90%以上。所以，剪力墙结构体系的优化，比如剪力墙的数量、布置以及尺寸的优化工作，即布置多少剪力墙，以及在什么位置才能最大限度地发挥剪力墙的作用，这些应当作为当前的重点工作予以关注。有数据表明，通过优化计算后的结构设计方案造价一般会比传统设计方案节约5% ～30%［2］，因此，研究高层剪力墙结构体系的结构优化设计工作，可使资源更加合理优化配置，具有良好的社会和经济效益。

国外学者在结构优化方面的研究起步较早。从二十世纪六七十年代起，国外学者就进行过剪力墙结构体系弹塑性力学性能的研究，其中以Kumarapillai K和Pekau C A等为代表，取得了卓著的成绩［3，4］。之后随着计算机信息技术的发展，计算能力日益提高，可用于结构优化的手段更加多样化。我国在剪力墙结构优化方面的研究有:傅学怡［5］给出了楼层断面剪力墙的计算公式;邵志坚［6］利用多组模型进行计算，得出了剪力墙的混凝土强度等级、墙率以及墙洞数量等因素对计算模型内力、刚度、位移等结果的影响;姚琦［7］通过优化计算，更改剪力墙布置获得了合理的结构刚度，实现了对整个剪力墙结构的优化。

以上研究，普遍是从单个剪力墙构件模型出发，在一定的条件下，得出构件响应与变量的影响关系，大多只实现了单目标下的剪力墙数量的选择，对剪力墙哪些位置设置洞口能达到最优目前还未见报道。对于实际的剪力墙结构，由于存在设计变量多、约束条件多、变量离散、受建筑功能限制较大等因素，因此前述文献中给出的公式对实际结构定量化优化缺少可操作性，对实现多目标下的高层剪力墙结构的剪力墙位置和数量的分析还有待研究。多目标结构优化设计将遗传算法等先进的方法引入到结构领域，是建筑结构设计领域未来的发展方向。

建筑结构设计中，在满足建筑功能和国家规范的前提下，基于“低碳、节能、环保”理念，对建筑结构进行优化设计，通过合理布置剪力墙位置以及合理选择各类构件的尺寸，不仅能使结构构件受力更加合理，而且可以节省材料，减小企业的资金压力。本文基于优化分析软件Isight和通用有限元软件Abaqus，通过二次开发将自编的C#和Python脚本程序嵌入优化平台，运用有限元生死单元技术，搭建了完整的可用于高层剪力墙结构体系优化设计的多目标优化流程，将传统被动设计变为精细化主动寻找相对最优解的过程，可以对设计师提供强有力的帮助。

1 结构多目标优化流程

1.1 多目标优化问题的数学描述

数学上，多目标优化问题可以描述为D个设计变量、N个目标函数、m+k个约束条件组成的一个求解问题。决策者根据具体问题要求在非劣解集中选择比较满意的一个非劣解作为最终解。多目标优化问题的数学形式可以如下描述［8］:

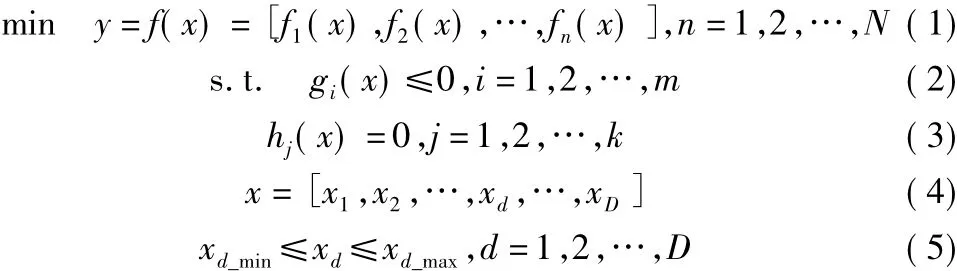
其中，x为一个维度为D的设计向量;y为目标函数向量，由多个目标函数组成;N为优化目标的数量;gi(x)≤0和hj(x)=0确定了解的可行域，xd_max和xd_min为每维向量搜索的上下限。

1.2 多目标优化流程设置

基于高层剪力墙初始结构设计方案，在不违反建筑功能和规范的前提下(比如避免出现短肢剪力墙)，在可能的位置上预先布置剪力墙，然后通过自编接口程序将模型转为Abaqus软件的输入文件，通过优化分析软件Isight搭建分析流程，并将自编脚本程序嵌入到流程中，对分组剪力墙单元进行敏度分析。之后根据敏度分析结果，剔除不敏感位置墙元(不敏感意味着此位置增加或减少墙对结构指标比如层间位移角影响不大)，从而达到剪力墙准拓扑相对最优分布。

基于上述结果，将多目标算法和结构、构件控制指标脚本嵌入优化平台，设定优化多目标、约束条件和设计变量，通过优化算法多次迭代后将优化结果回代常规设计软件进行配筋计算比较，取相对优化结果作为最终剪力墙构型。这种方法实际上属于一定约束条件下的结构准拓扑优化，是对材料满足约束条件下的合理分布，实现物尽其用，进而达到拓扑层次的优化。在剪力墙拓扑分布优化的前提下，对结构构件进行尺寸优化。结构敏度分析和整体优化流程如图1所示。

2 工程算例

2.1 工程概况

合肥置地广场·栢悦公馆8号楼位于安徽省合肥市政务文化新区，项目总占地面积为51 188 m2，总建筑面积为380 000 m2，结构三维模型如图2所示。

图1 结构敏度和优化分析流程

图2 结构三维模型图

本结构为高层住宅，塔楼地上41层，地下2层，结构屋面高度122.75 m，采用剪力墙结构体系。以地下室顶板面为计算嵌固端，重力荷载代表值为4.43×104t，以平地震荷载为控制荷载，结构第一周期3.13 s，振型为Y向平动。

2.2 工程模型与计算参数

本工程所在场地的特征周期为0.35 s，选用弹性动力时程分析，取地震荷载时长为40 s，时间步长为0.01 s，地震加速度的峰值为 344.5 cm/s2。

计算选取地下室顶板以上部分作为弹性动力时程分析的对象，从地下室顶板处竖向构件的端点输入计算选取的地震波。有限元分析模型包含弹性壳单元和弹性梁单元，梁、柱用可考虑线性剪切效应的一阶三维梁单元B31模拟，墙、楼板等用4节点缩减积分曲壳单元S4R和S3模拟。

2.3 优化结果分析

本工程实例计算条件设定如下:

多目标函数:结构的造价和第一阶周期(假设钢筋价格为3 500元/t，混凝土价格为450元/m3)。

约束条件:楼层层间位移角不大于1/1 000;墙轴压比限值0.5;扭转平动周期比不大于0.85。

设计变量:分组剪力墙单元的材料属性。

优化前后剪力墙标准层结构平面图对比如图3，图4所示。

图3 初始设计标准层结构平面图

在层间位移角、轴压比、扭转平动位移比等约束都满足的条件下，优化前后结构造价对比见图5。结果表明，与传统结构设计方法相比，多目标优化方法在满足各项约束指标的前提下，能进一步优化，实现了自动寻优精细化设计，减少了建筑的材料用量，达到了建筑节能的目标。

图4 优化设计标准层结构平面图

图5 结构优化前后造价对比

3 结语

本文开发了一套完整的高层剪力墙结构多目标优化流程，可以实现高层剪力墙结构的准拓扑优化和墙尺寸优化，并通过工程算例验证了其实用性，初步实现了对高层剪力墙结构体系和尺寸的优化，弥补了传统工程设计的不足，为实现自动化、智能化结构设计提供了切实可行的思路。